Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
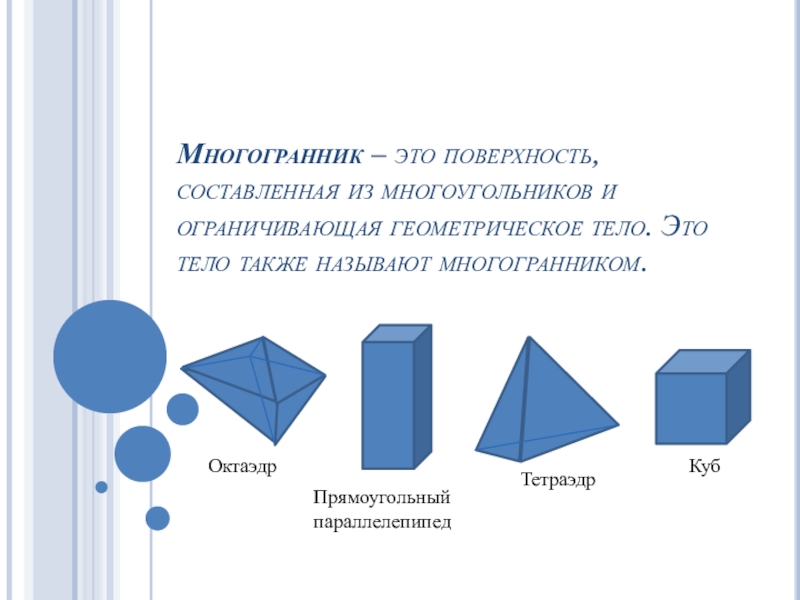
Многогранник – это поверхность, составленная из многоугольников и
Содержание
- 1. Многогранник – это поверхность, составленная из многоугольников и
- 2. МногогранникиМногоугольники, из которых составлен многогранник, называются гранями.Стороны
- 3. Многогранники бывают выпуклыми и невыпуклыми. Выпуклый многогранник
- 4. ПризмаПризмой называется многогранник, у которого две грани
- 5. Призмы бывают прямыми и наклонными.
- 6. Прямая призма, основаниями которой являются правильные многоугольники,
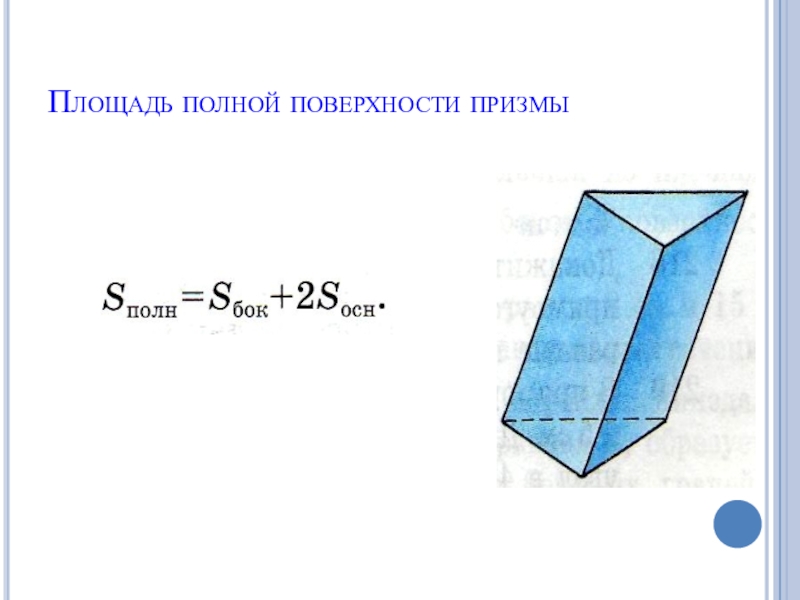
- 7. Площадь полной поверхности призмы
- 8. Площадь боковой поверхности призмыТЕОРЕМА:Площадь боковой поверхности прямой призмы равна половине произведения периметра основания на высоту призмы.
- 9. Объем наклонной призмы ТЕОРЕМА:Объем наклоннойпризмы равенпроизведению площадиоснования на высоту.
- 10. ОпределениеПирамида – это многоугольник А1А2…Аn и точка
- 11. Элементы пирамидыоснование — многоугольник, которому не принадлежит
- 12. Свойства пирамидыЕсли боковые грани наклонены к плоскости
- 13. Свойства пирамидыЕсли все боковые ребра равны, то:около
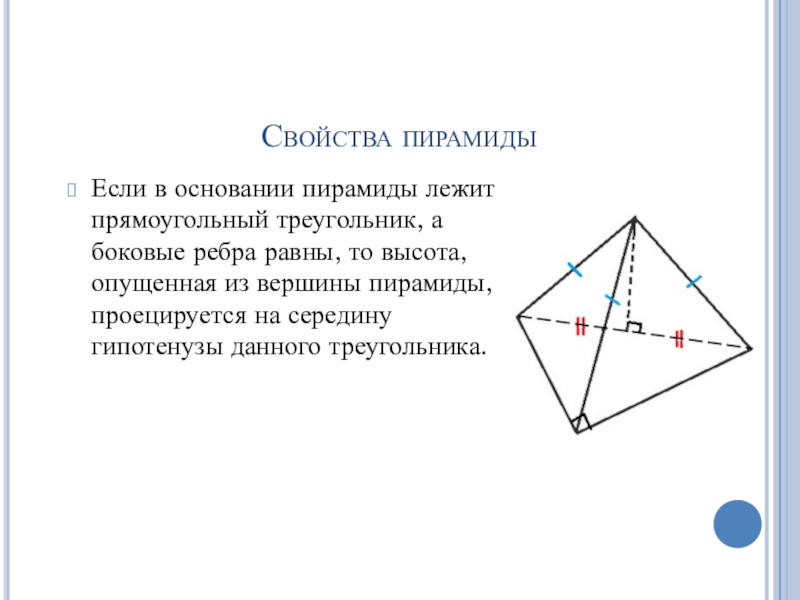
- 14. Свойства пирамидыЕсли в основании пирамиды лежит прямоугольный
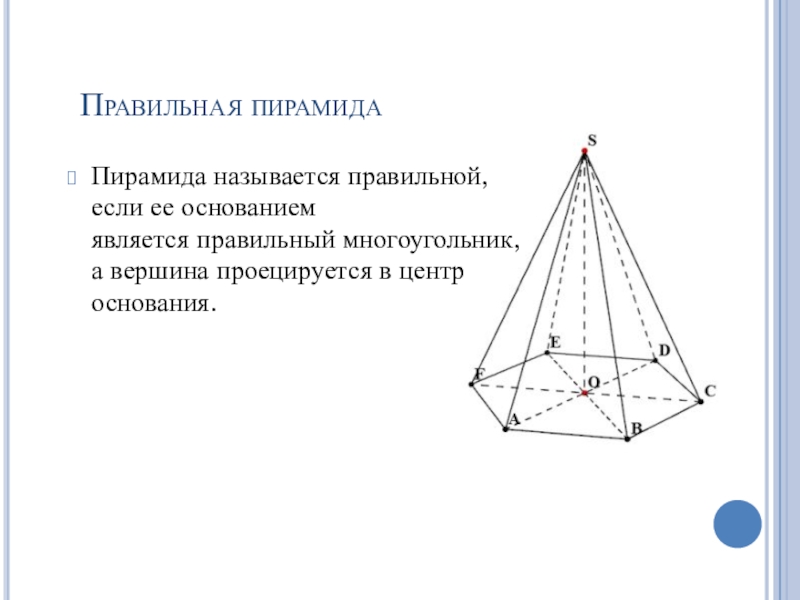
- 15. Правильная пирамидаПирамида называется правильной, если ее основанием является правильный многоугольник, а вершина проецируется в центр основания.
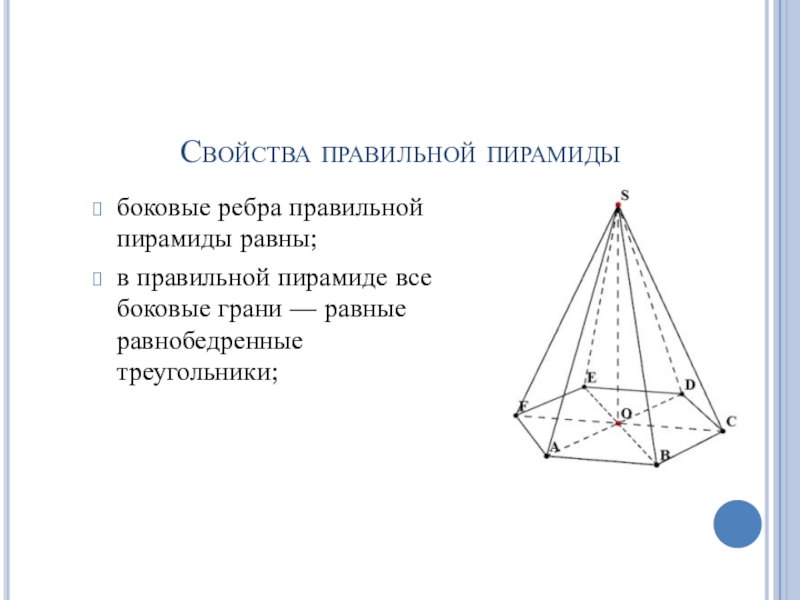
- 16. Свойства правильной пирамидыбоковые ребра правильной пирамиды равны;в правильной пирамиде все боковые грани — равные равнобедренные треугольники;
- 17. Прямоугольная пирамидаПирамида называется прямоугольной, если одно из
- 18. Поверхность пирамидыПлощадью полной поверхности пирамиды называется сумма
- 19. Формулы, связанные с пирамидойЧтобы определить площадь боковой
- 20. Формулы, связанные с пирамидой
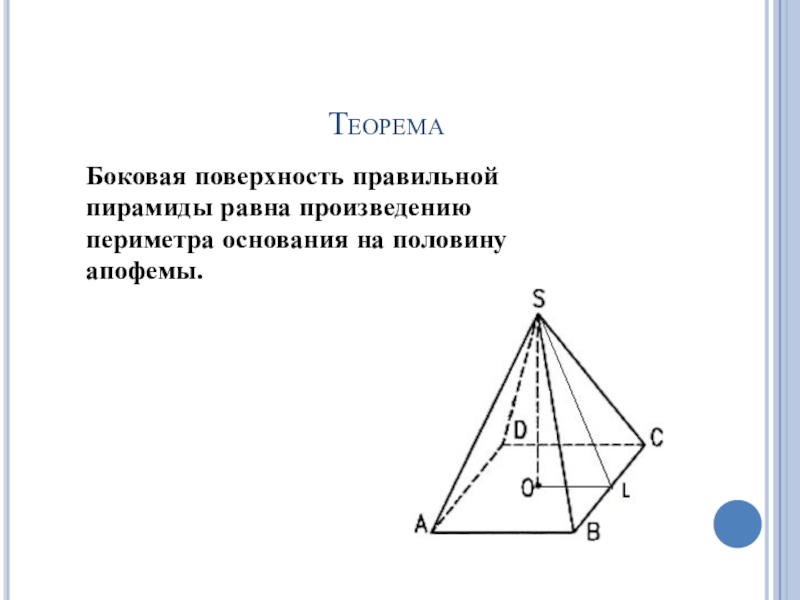
- 21. Теорема Боковая поверхность правильной пирамиды равна произведению периметра основания на половину апофемы.
- 22. Формулы, связанные с пирамидой
- 23. Скачать презентанцию
МногогранникиМногоугольники, из которых составлен многогранник, называются гранями.Стороны граней называются рёбрами.А концы рёбер называют вершинами многоугольника.Гранью куба является квадратАВАВ является ребром кубаАА является вершиной куба
Слайды и текст этой презентации
Слайд 1Многогранник – это поверхность, составленная из многоугольников и ограничивающая геометрическое
тело. Это тело также называют многогранником.
Слайд 2Многогранники
Многоугольники, из которых составлен многогранник, называются гранями.
Стороны граней называются рёбрами.
А
концы рёбер называют вершинами многоугольника.
Гранью куба является квадрат
А
В
АВ является ребром
кубаА
А является вершиной куба
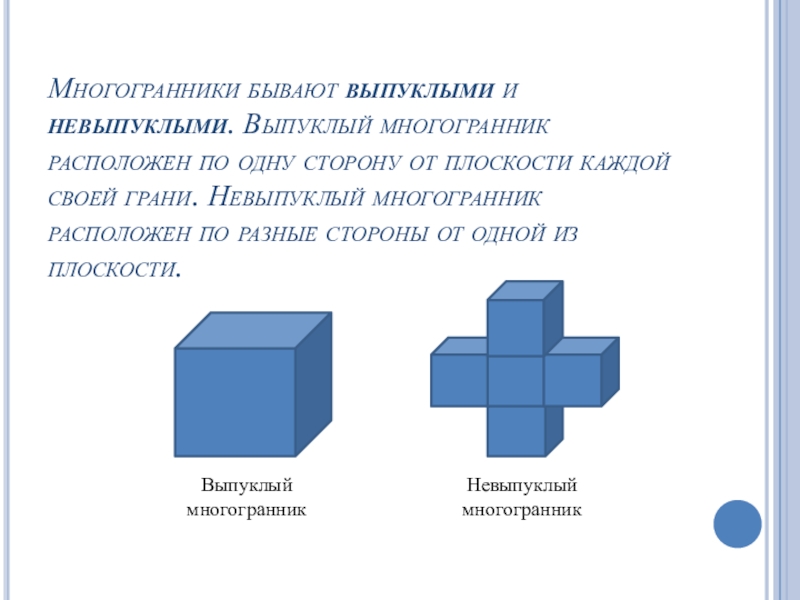
Слайд 3Многогранники бывают выпуклыми и невыпуклыми. Выпуклый многогранник расположен по одну
сторону от плоскости каждой своей грани. Невыпуклый многогранник расположен по
разные стороны от одной из плоскости.Выпуклый
многогранник
Невыпуклый многогранник
Слайд 4Призма
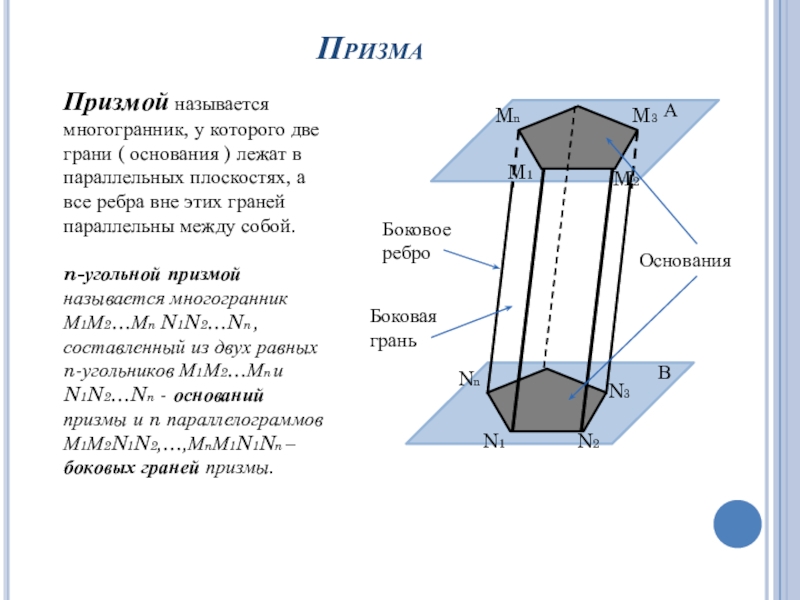
Призмой называется многогранник, у которого две грани ( основания )
лежат в параллельных плоскостях, а все ребра вне этих граней
параллельны между собой.n-угольной призмой называется многогранник М1М2…Мn N1N2…Nn , составленный из двух равных n-угольников М1М2…Мn и N1N2…Nn - оснований призмы и n параллелограммов М1М2N1N2,…,МnМ1N1Nn – боковых граней призмы.
А
В
M1
M2
M3
Mn
Nn
N1
N2
N3
Боковое
ребро
Боковая грань
Основания
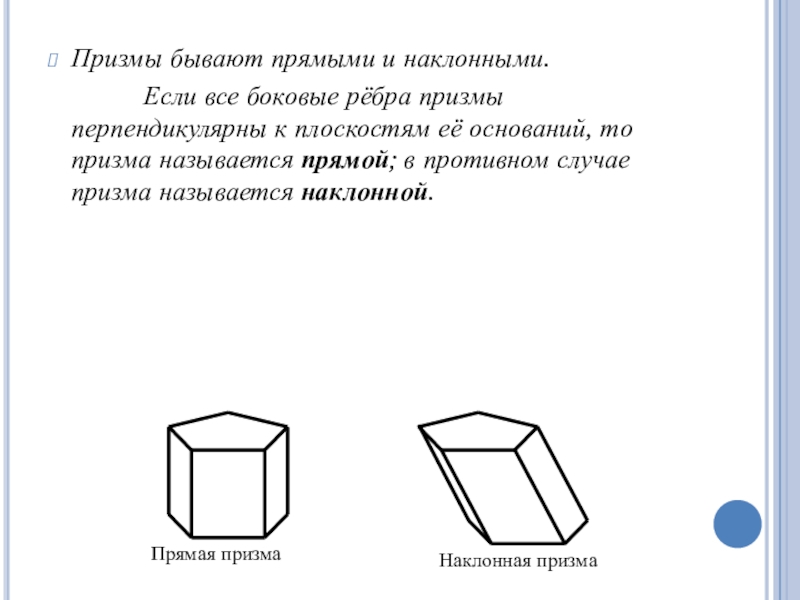
Слайд 5Призмы бывают прямыми и наклонными.
Если все боковые рёбра призмы перпендикулярны к плоскостям её
оснований, то призма называется прямой; в противном случае призма называется наклонной.Прямая призма
Наклонная призма
Слайд 6
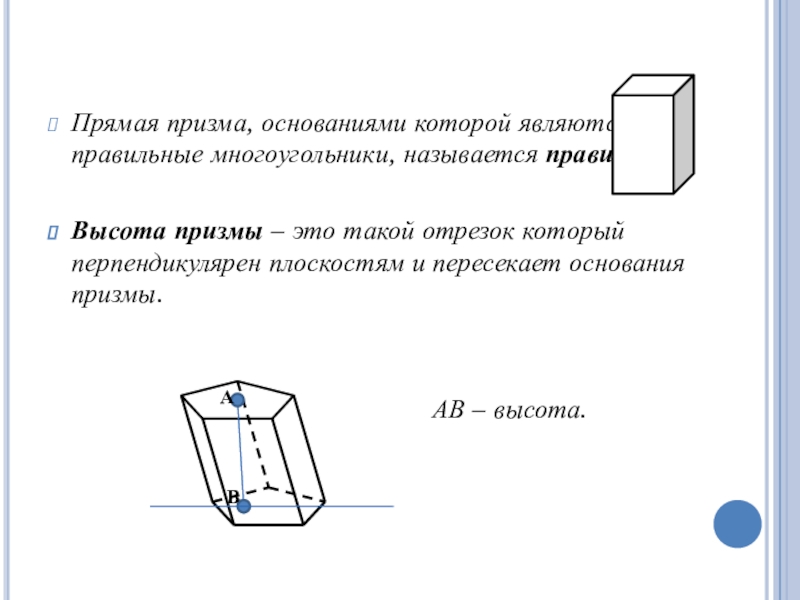
Прямая призма, основаниями которой являются правильные многоугольники, называется правильной.
Высота призмы
– это такой отрезок который перпендикулярен плоскостям и пересекает основания
призмы.АВ – высота.
А
В
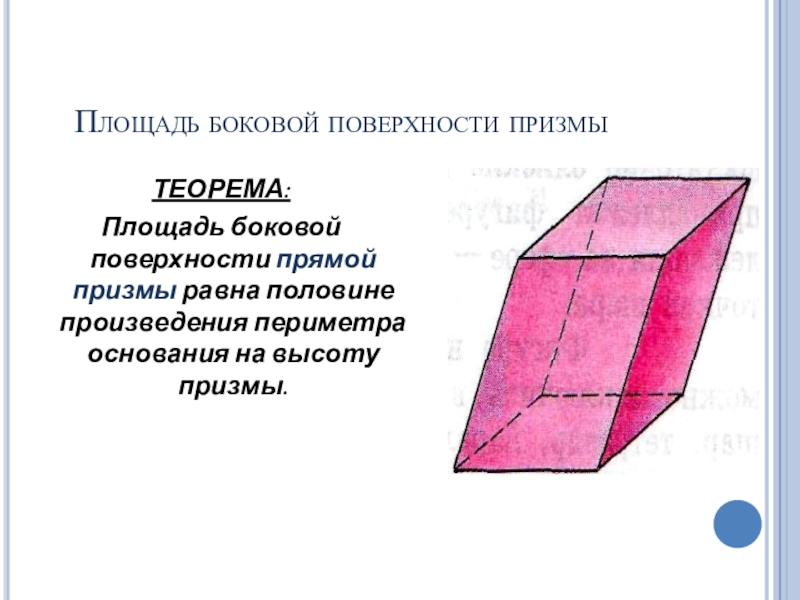
Слайд 8Площадь боковой поверхности призмы
ТЕОРЕМА:
Площадь боковой поверхности прямой призмы равна половине
произведения периметра основания на высоту призмы.
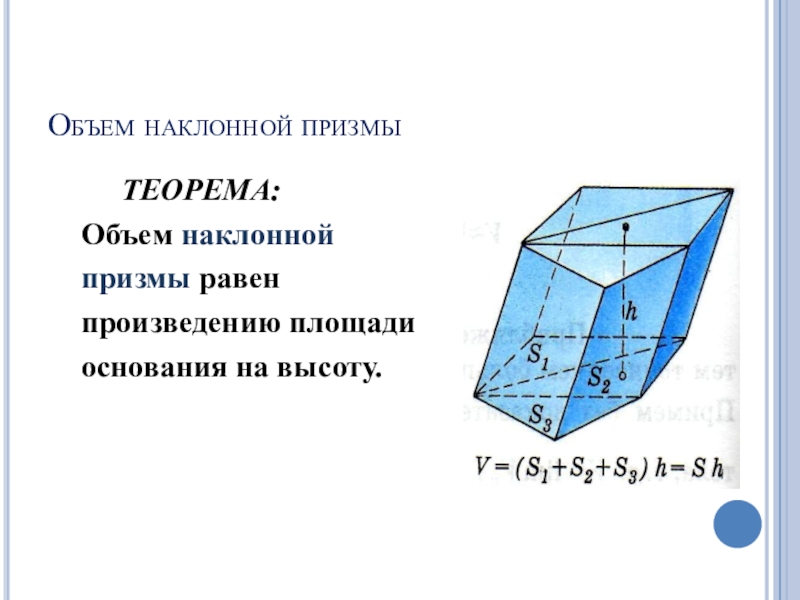
Слайд 9Объем наклонной призмы
ТЕОРЕМА:
Объем наклонной
призмы равен
произведению площади
основания на высоту.
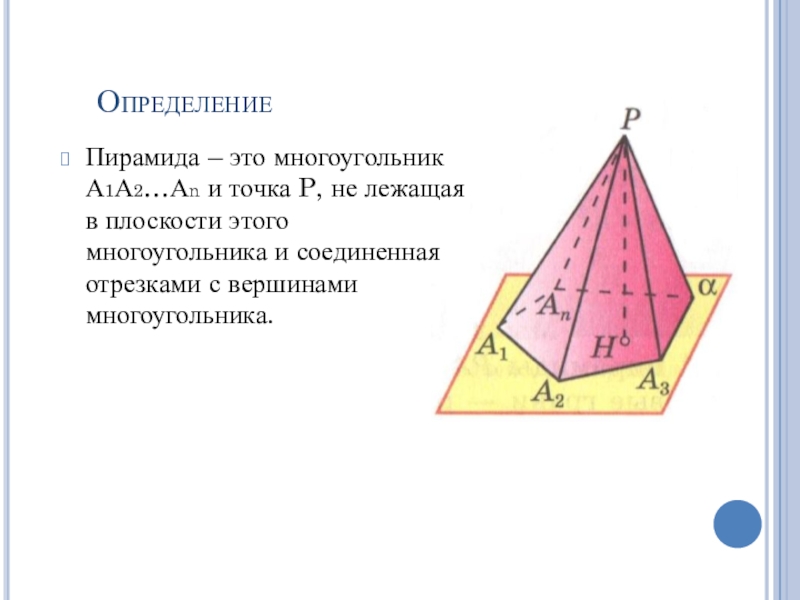
Слайд 10Определение
Пирамида – это многоугольник А1А2…Аn и точка P, не лежащая
в плоскости этого многоугольника и соединенная отрезками с вершинами многоугольника.
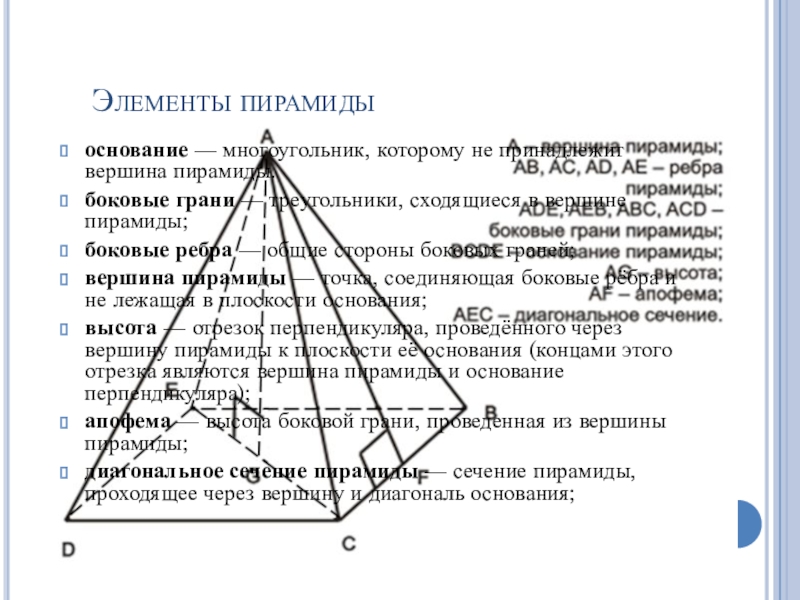
Слайд 11Элементы пирамиды
основание — многоугольник, которому не принадлежит вершина пирамиды.
боковые грани
— треугольники, сходящиеся в вершине пирамиды;
боковые ребра — общие стороны
боковых граней;вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания;
высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра);
апофема — высота боковой грани, проведенная из вершины пирамиды;
диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания;
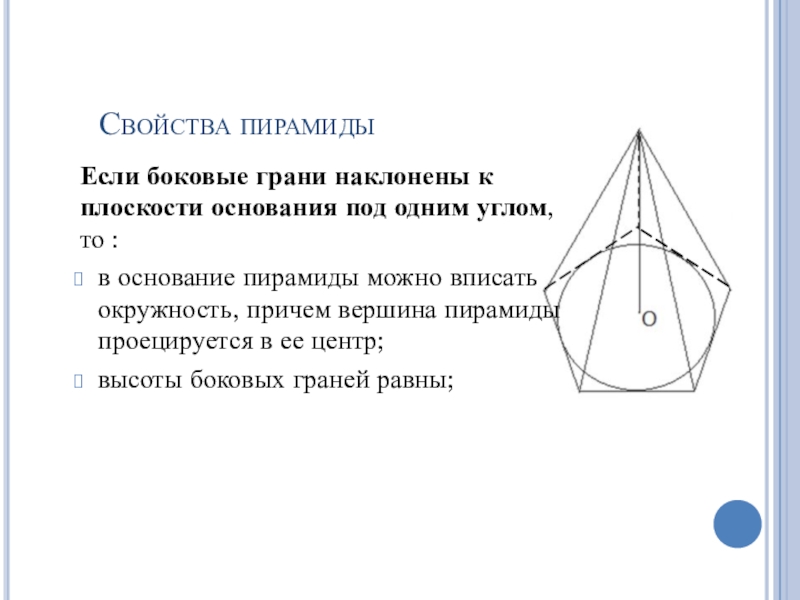
Слайд 12Свойства пирамиды
Если боковые грани наклонены к плоскости основания под одним
углом, то :
в основание пирамиды можно вписать окружность, причем
вершина пирамиды проецируется в ее центр;высоты боковых граней равны;
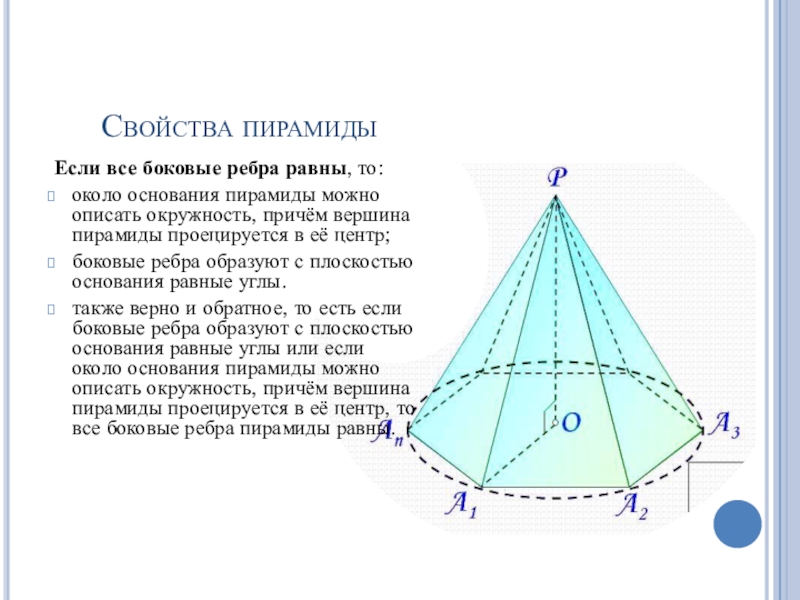
Слайд 13Свойства пирамиды
Если все боковые ребра равны, то:
около основания пирамиды можно
описать окружность, причём вершина пирамиды проецируется в её центр;
боковые ребра
образуют с плоскостью основания равные углы.также верно и обратное, то есть если боковые ребра образуют с плоскостью основания равные углы или если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.
Слайд 14Свойства пирамиды
Если в основании пирамиды лежит прямоугольный треугольник, а боковые
ребра равны, то высота, опущенная из вершины пирамиды, проецируется на
середину гипотенузы данного треугольника.
Слайд 15Правильная пирамида
Пирамида называется правильной, если ее основанием является правильный многоугольник, а
вершина проецируется в центр основания.
Слайд 16Свойства правильной пирамиды
боковые ребра правильной пирамиды равны;
в правильной пирамиде все
боковые грани — равные равнобедренные треугольники;
Слайд 17Прямоугольная пирамида
Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды
перпендикулярно основанию. В данном случае, это ребро и является высотой
пирамиды.
Слайд 18Поверхность пирамиды
Площадью полной поверхности пирамиды называется сумма площадей всех ее
граней (т.е. основания и боковых граней).
Площадью боковой поверхности пирамиды называется
сумма площадей ее боковых граней.
Слайд 19Формулы, связанные с пирамидой
Чтобы определить площадь боковой поверхности пирамиды, надо
найти сумму площадей всех её боковых граней:
Слайд 21Теорема
Боковая поверхность правильной пирамиды равна произведению периметра основания на
половину апофемы.
