Многогранники Геометрия 10

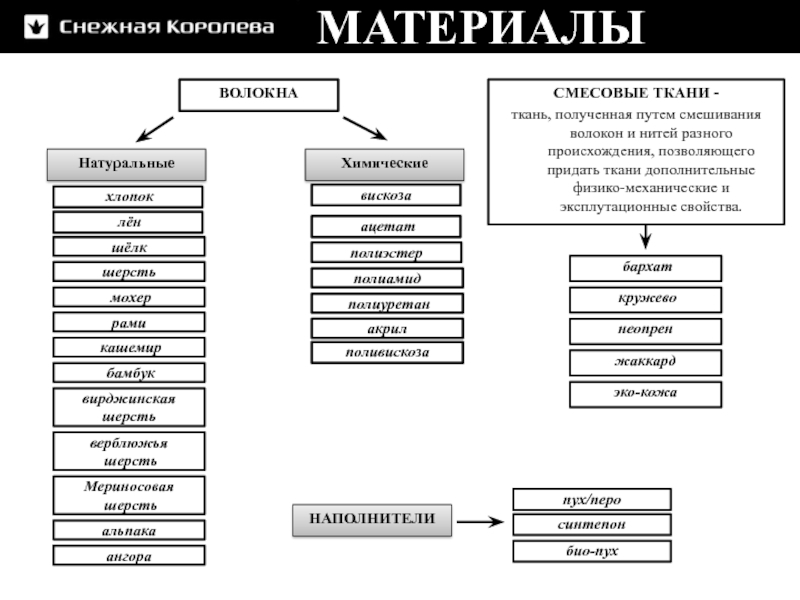
называется тело,
поверхность которого
состоит из конечного
числа многоугольников,
называемых

Стороны и вершины этих многоугольников
называются ребрами и вершинами.

из шести параллелограммов
Параллелепипед называется прямоугольным, если все его грани прямоугольники
Куб
Прямоугольный

Параллелепипед

параллелограммов, имеющих общие стороны с каждым из оснований.
вы
с
ота
п
р
я
м
а
я
н
а
к
л
о
н
н
а
я
Призма
Два равных многоугольника

Параллелограммы называют
боковыми гранями призмы

Перпендикуляр, проведенный из вершины одного
основания к плоскости другого основания называют
высотой.

призмы равна произведению периметра основания
на высоту.
Sбок. = ah +

Sполн. =

вершину
Многоугольник называют основанием пирамиды
Треугольники называют боковыми гранями
Общую вершину называют вершиной

Перпендикуляр РН называют высотой

Sбок. + Sосн.

Н

Р

Пирамида

Sполн. =

апофемой
Теорема: Площадь боковой поверхности правильной
пирамиды равна половине произведения

Р

Е

Правильная пирамида

Боковые ребра равны

Боковые грани – равные равнобедренные треугольники

Основание высоты совпадает
с центром вписанной или
описанной окружности

пирамиды равна половине произведения
полусуммы периметров оснований на апофему

2.
4
4
6
8
6
12
20
12
30
12
20
30
6
8
12