Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
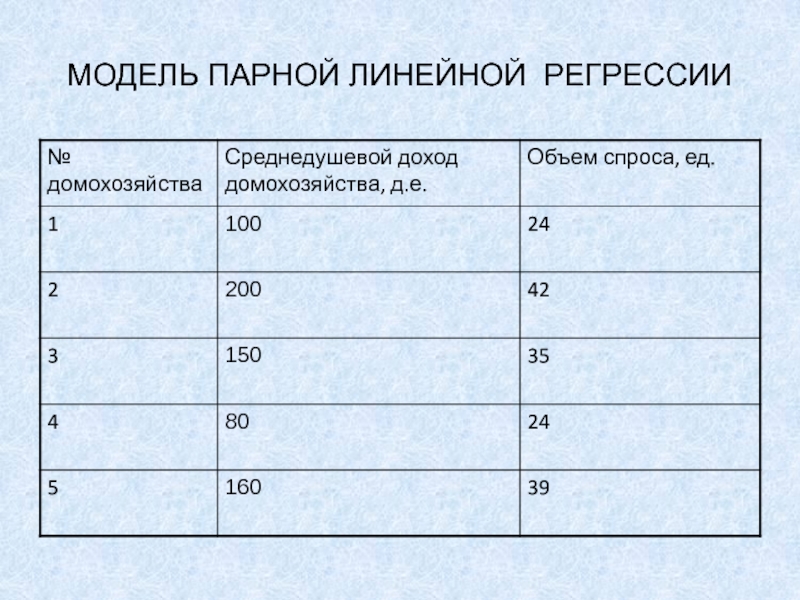
МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
Содержание
- 1. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
- 2. y=0,17x+9,33 - функция спроса в зависимости от
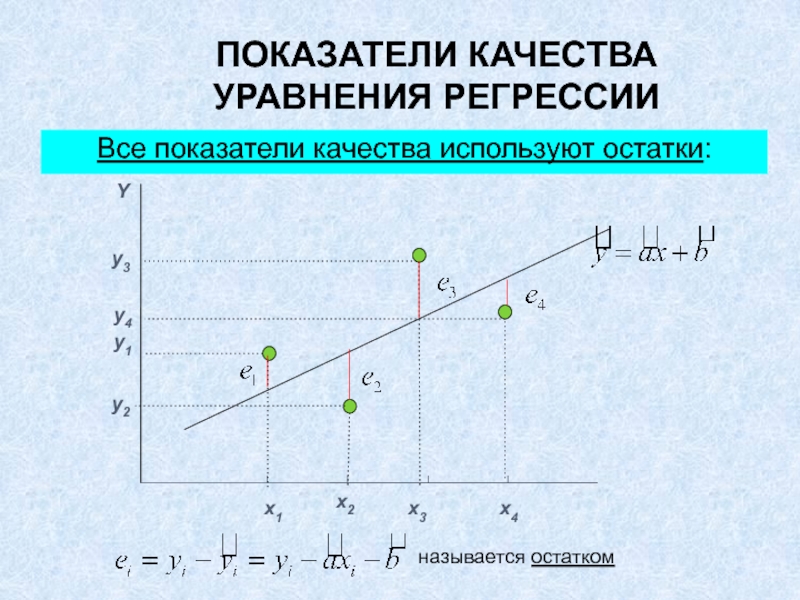
- 3. ПОКАЗАТЕЛИ КАЧЕСТВА УРАВНЕНИЯ РЕГРЕССИИВсе показатели качества используют остатки:Yy2y1y4y3x1x2x3x4называется остатком
- 4. Как оценить качество построенной модели?Построим прогноз по модели по формуле
- 5. Как оценить качество построенной модели?Вычисляем остатки
- 6. Как оценить качество построенной модели?Находим относительную ошибку аппроксимацииПроцентный формат
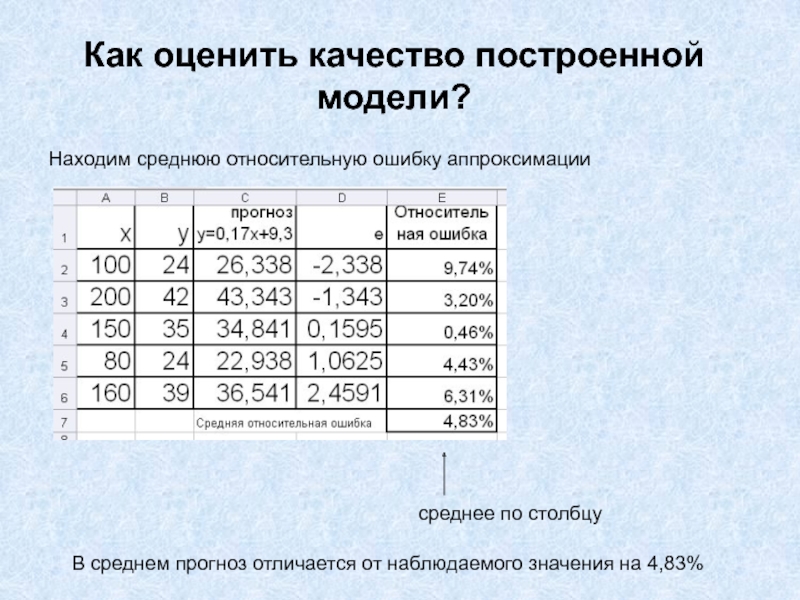
- 7. Как оценить качество построенной модели?Находим среднюю относительную
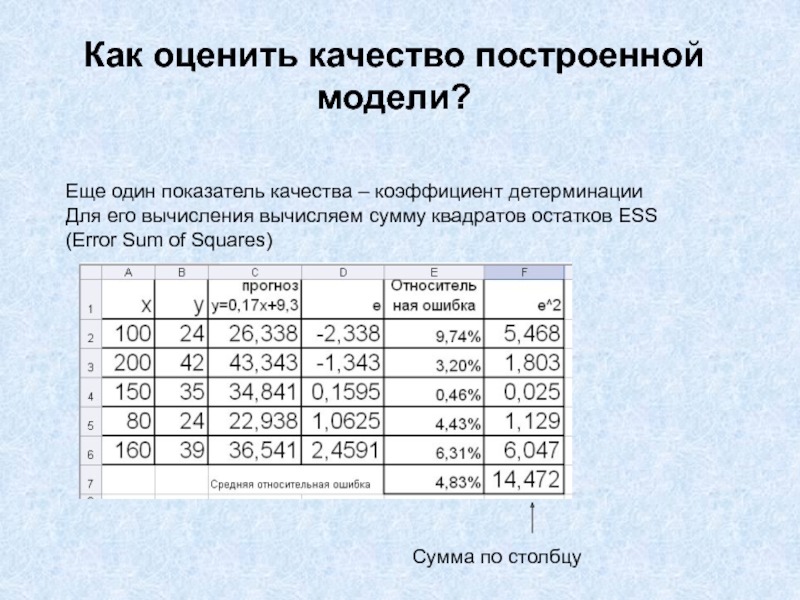
- 8. Как оценить качество построенной модели?Еще один показатель
- 9. Вычисляем суммы квадратов - остаточную, регрессионную и
- 10. Коэффициент детерминации R2 Коэффициентом детерминации называют числоКоэффициентом
- 11. Свойства коэффициента детерминации R2 1)
- 12. Свойства коэффициента детерминации R2 2) Если
- 13. Свойства коэффициента детерминации R2 3) Если
- 14. Свойства коэффициента детерминации R2 4) В случае парной линейной регрессии
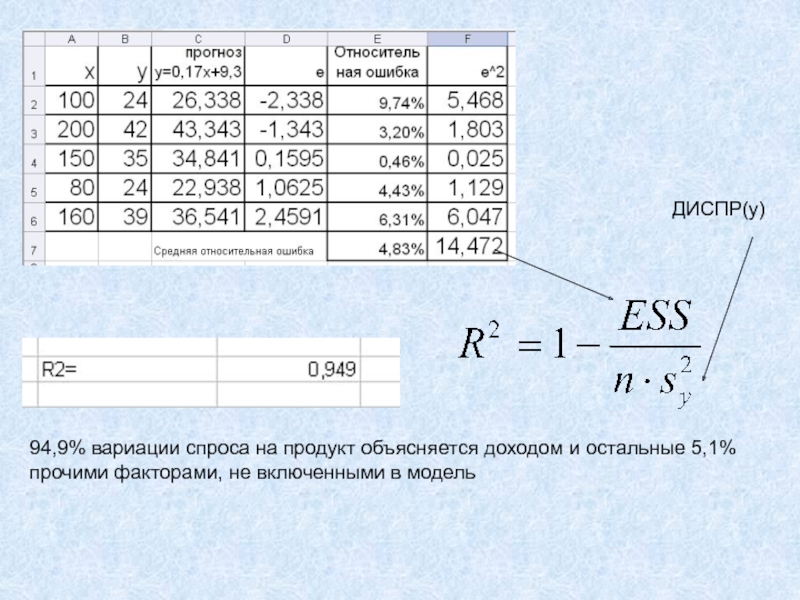
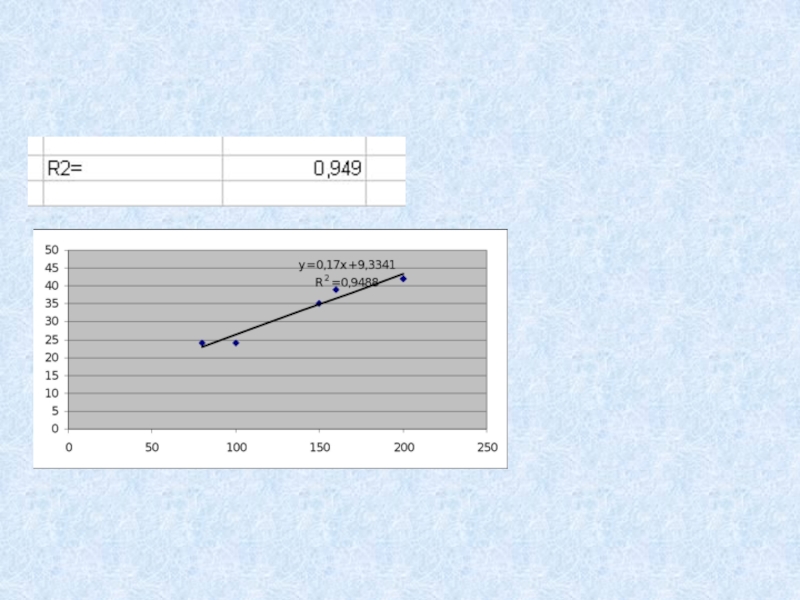
- 15. 94,9% вариации спроса на продукт объясняется доходом и остальные 5,1%прочими факторами, не включенными в модельДИСПР(y)
- 16. Слайд 16
- 17. Стандартная ошибка регрессии (средняя квадратическая ошибка) s
- 18. Пример построения уравнения регрессииПри анализе зависимости
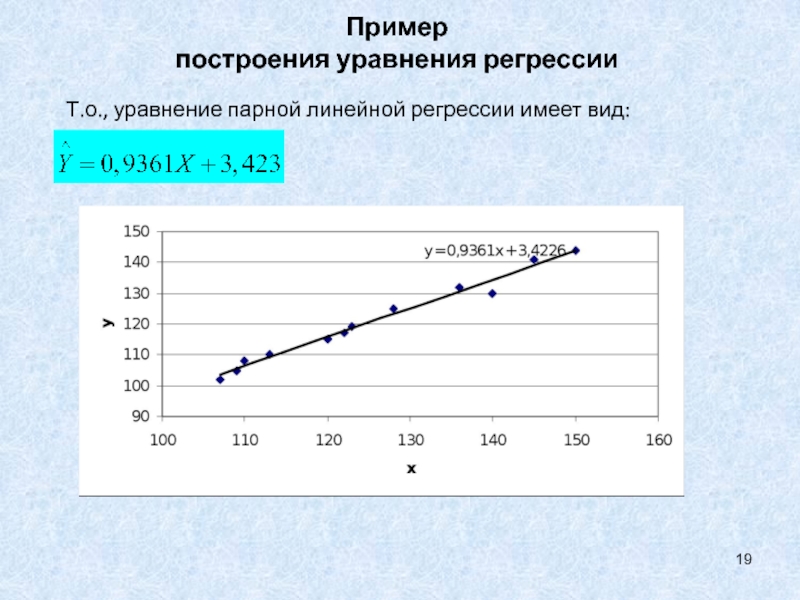
- 19. Пример построения уравнения регрессииТ.о., уравнение парной линейной регрессии имеет вид:
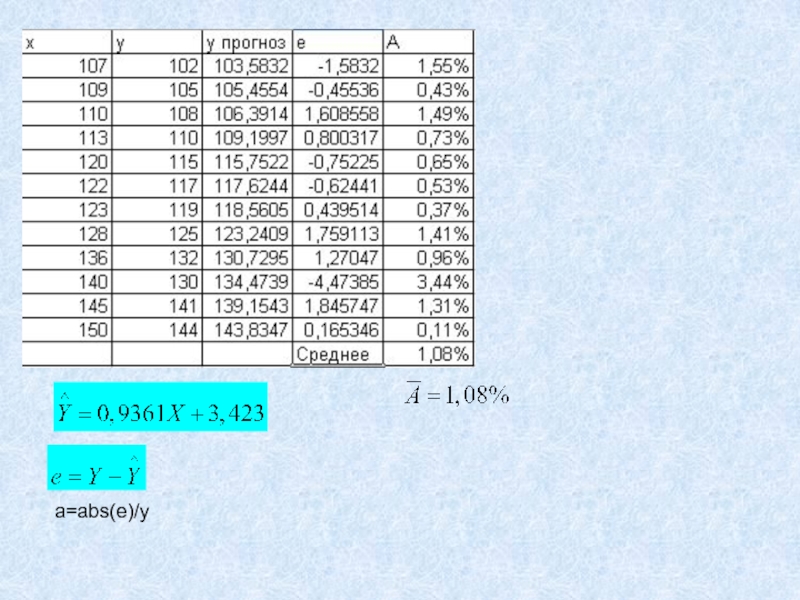
- 20. Пример построения уравнения регрессии
- 21. a=abs(e)/y
- 22. ПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИДанные 2002 г. о
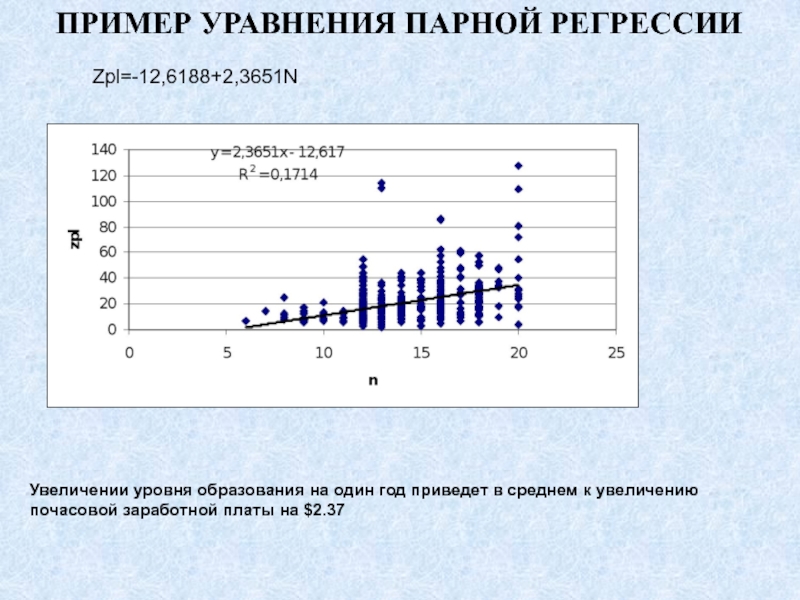
- 23. ПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИZpl=-12,6188+2,3651NУвеличении уровня образования на
- 24. ПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИZpl=-12,6168+2,3651N
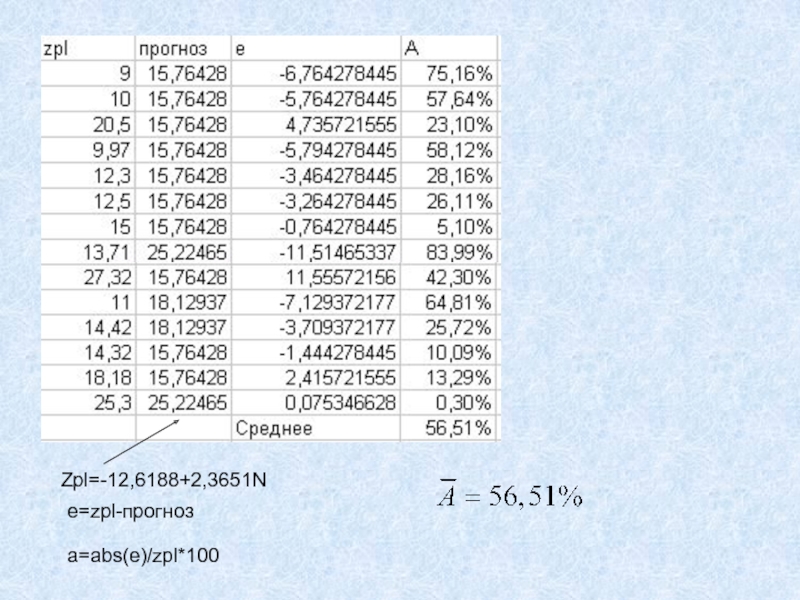
- 25. e=zpl-прогнозa=abs(e)/zpl*100Zpl=-12,6188+2,3651N
- 26. Скачать презентанцию
y=0,17x+9,33 - функция спроса в зависимости от дохода.С ростом дохода на 1 ден.ед. спрос на товар растет на 0,17 ед.Сервис – Анализ данных
Слайды и текст этой презентации
Слайд 2y=0,17x+9,33 - функция спроса в зависимости
от дохода.
С ростом дохода
на 1 ден.ед. спрос на товар
– Анализ данных
Слайд 3ПОКАЗАТЕЛИ КАЧЕСТВА УРАВНЕНИЯ РЕГРЕССИИ
Все показатели качества используют остатки:
Y
y2
y1
y4
y3
x1
x2
x3
x4
называется остатком
Слайд 6Как оценить качество построенной модели?
Находим относительную ошибку аппроксимации
Процентный формат
Слайд 7Как оценить качество построенной модели?
Находим среднюю относительную ошибку аппроксимации
среднее по
столбцу
В среднем прогноз отличается от наблюдаемого значения на 4,83%
Слайд 8Как оценить качество построенной модели?
Еще один показатель качества – коэффициент
детерминации
Для его вычисления вычисляем сумму квадратов остатков ESS
(Error Sum of
Squares)Сумма по столбцу
Слайд 9Вычисляем суммы квадратов
- остаточную, регрессионную и общую
– error sum of
squares, остаточная сумма квадратов
отклонений
– total sum of
squares, общая сумма квадратов отклонений
– regression sum of squares, регрессионная сумма
квадратов отклонений
Теорема TSS=RSS+ESS
Слайд 10Коэффициент детерминации R2
Коэффициентом детерминации называют число
Коэффициентом детерминации - это доля
дисперсии признака y, объясненная
регрессией в общей дисперсии признака y
Слайд 12Свойства коэффициента детерминации R2
2) Если
, то линия регрессии точно соответствует всем
наблюдениями между x и y существует линейная функциональная зависимость.
Слайд 13Свойства коэффициента детерминации R2
3) Если
, то линия регрессии параллельна оси абсцисс
и переменная yне зависит от переменной x.
Слайд 1594,9% вариации спроса на продукт объясняется доходом и остальные 5,1%
прочими
факторами, не включенными в модель
ДИСПР(y)
Слайд 18Пример
построения уравнения регрессии
При анализе зависимости объема потребления Y (у.е.)
домохозяйства от располагаемого дохода X (у.е.) отобрана выборка объема n
= 12 (помесячно в течение года), результаты которой приведены в таблице:
Слайд 22
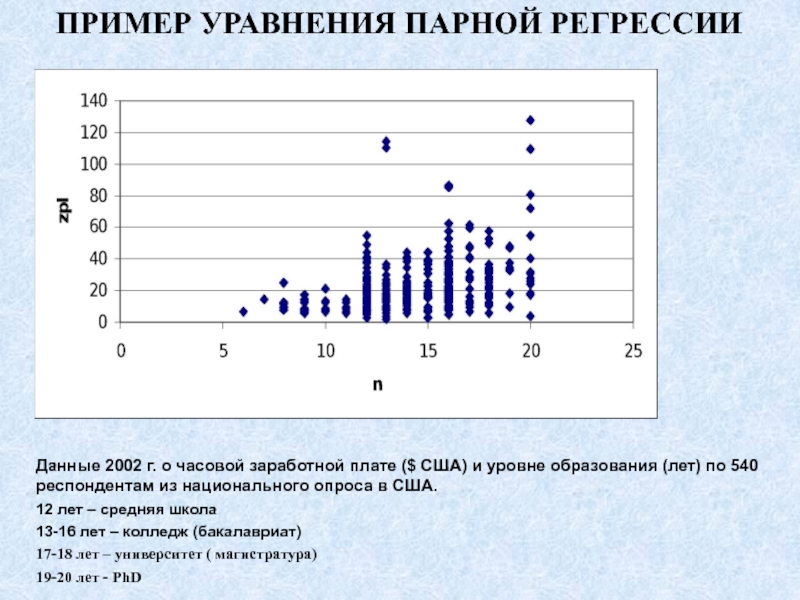
ПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИ
Данные 2002 г. о часовой заработной плате
($ США) и уровне образования (лет) по 540 респондентам из
национального опроса в США.12 лет – средняя школа
13-16 лет – колледж (бакалавриат)
17-18 лет – университет ( магистратура)
19-20 лет - PhD
Слайд 23ПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИ
Zpl=-12,6188+2,3651N
Увеличении уровня образования на один год приведет
в среднем к увеличению почасовой заработной платы на $2.37
