Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Модели биологических аналогий
Содержание
- 1. Модели биологических аналогий
- 2. Средства и методы моделированияМетоды моделирования – методы
- 3. Пример. Рост колонии микроорганизмовЗа время
- 4. Пример. Рост колонии микроорганизмовВ простейшем случае, когда
- 5. Пример. Рост колонии микроорганизмовГрафик функции
- 6. Уравнение ФерхюльстаЛогистическое уравнение было предложено Ферхюльстом в
- 7. Динамика численности в логистической модели при разных
- 8. Системы двух автономных дифференциальных уравнений Рассмотрим
- 9. Фазовая плоскостьПлоскость всех точек M(x,y) называется фазовой
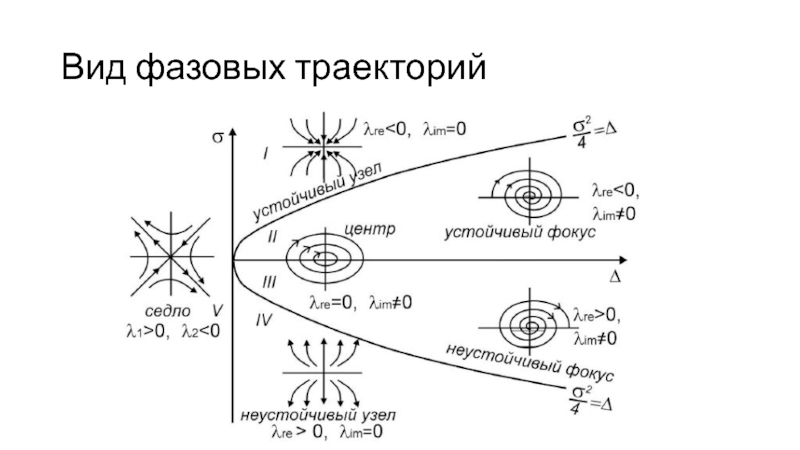
- 10. Фазовый портретСовокупность фазовых траекторий при различных начальных
- 11. Направление вектора dy/dx
- 12. Фазовые траекторий в аналитическом виде дает семейство интегральных кривых уравнения - фазовых траекторий системы на плоскости
- 13. Линейные системыРассмотрим системуa, b, c, d = const
- 14. Вид фазовых траекторий
- 15. Математические модели взаимодействия двух видов. Гипотезы Вольтерра1.
- 16. Математические модели взаимодействия двух видов. Гипотезы Вольтерра4.
- 17. Уравнения Вольтерраx1, x2 – численности видовai –
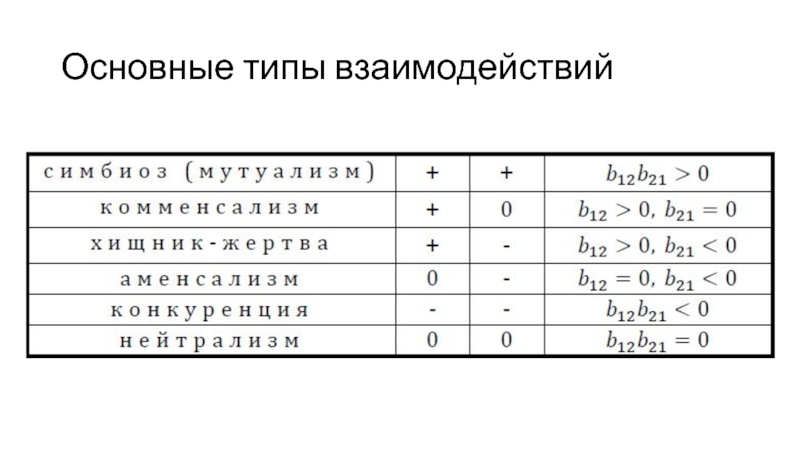
- 18. Основные типы взаимодействий
- 19. Уравнения конкуренции
- 20. Стационарные решения
- 21. Условие сосуществования видовНеобходимое условие устойчивости
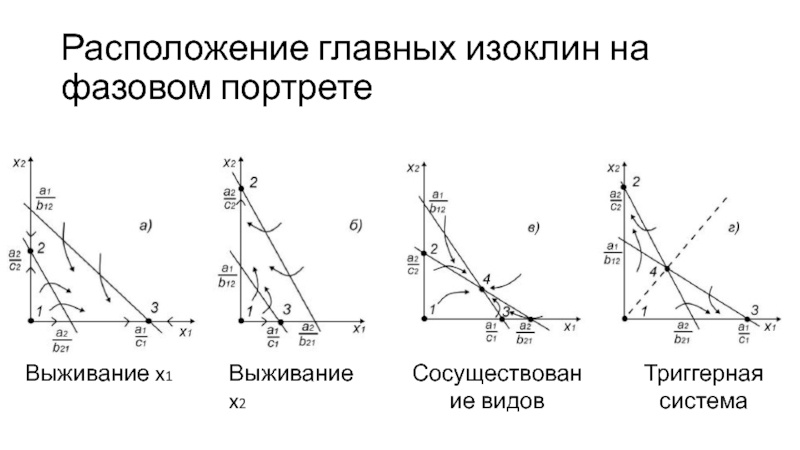
- 22. Расположение главных изоклин на фазовом портретеВыживание x1Выживание x2Сосуществование видовТриггерная система
- 23. Система «хищник-жертва»
- 24. Стационарные решения системы
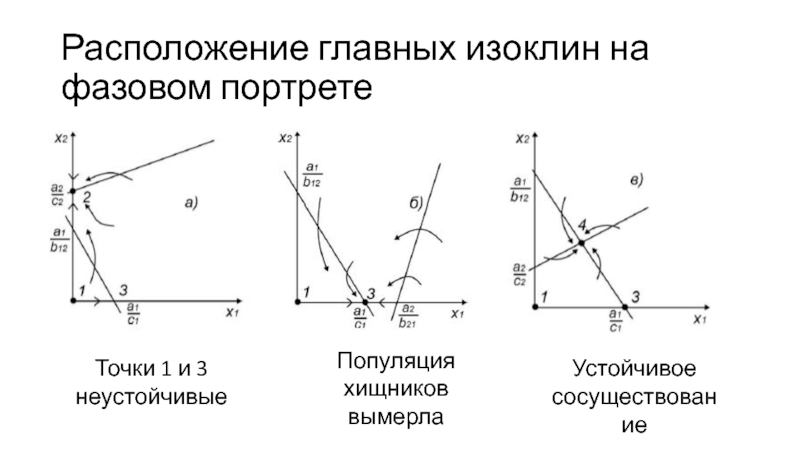
- 25. Расположение главных изоклин на фазовом портрете Устойчивое сосуществованиеПопуляция хищников вымерлаТочки 1 и 3 неустойчивые
- 26. Моделирование динамики популяций с помощью уравнений Лотка-ВольтерраМодель
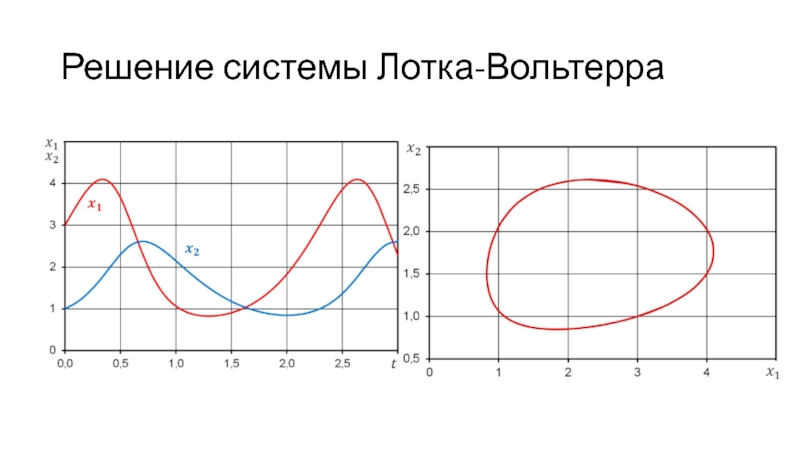
- 27. Решение системы Лотка-Вольтерра
- 28. Уравнения Лотка-Вольтерра с логистической поправкойМодель конкурирующих видов с логистической поправкой
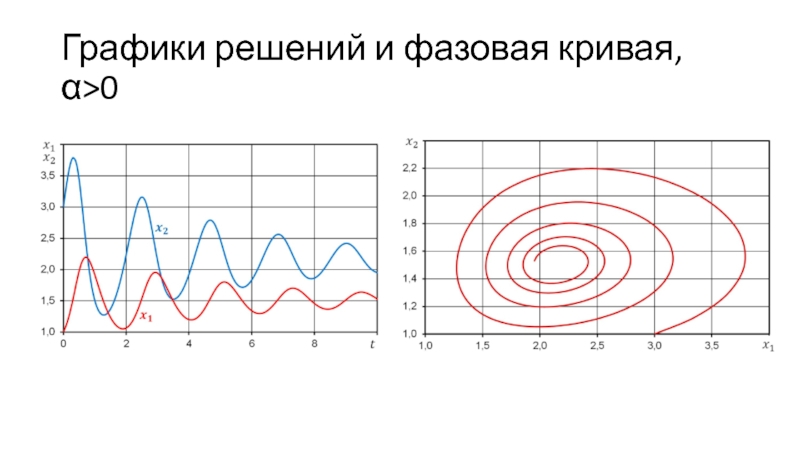
- 29. Графики решений и фазовая кривая, α>0
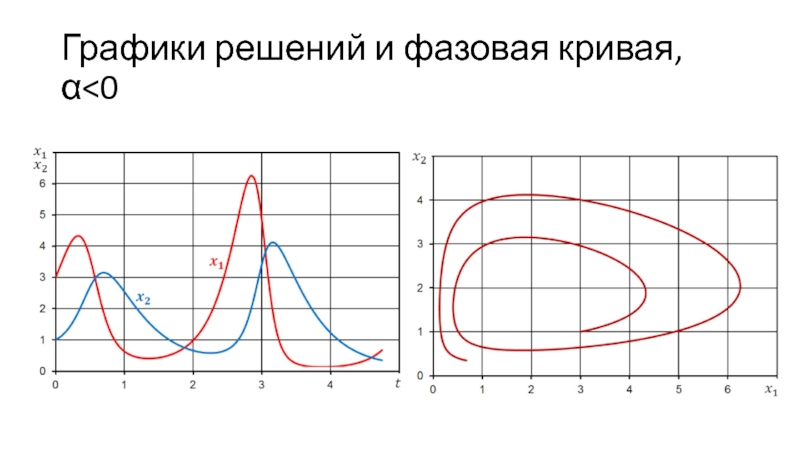
- 30. Графики решений и фазовая кривая, α
- 31. Модель Холлинга-ТэннераСкорость роста популяции жертв dx1⁄dt в этой модели равна сумме трех величин
- 32. Модель Холлинга-ТэннераСкорость роста популяции хищников dx2⁄dt строится
- 33. Модель Холлинга-ТэннераПри
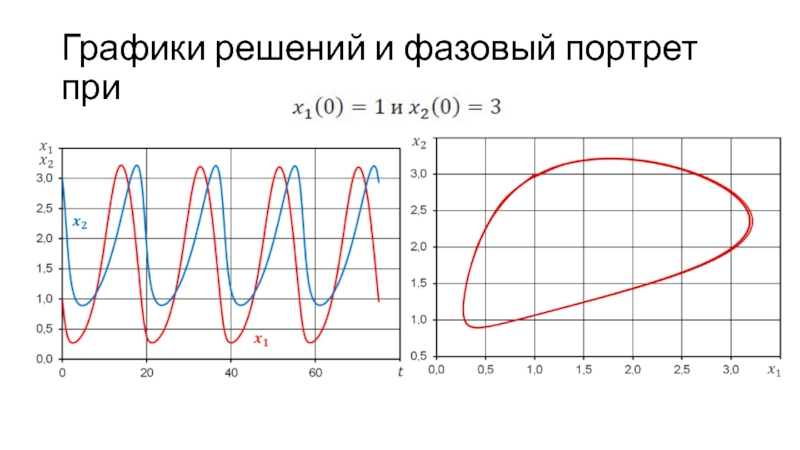
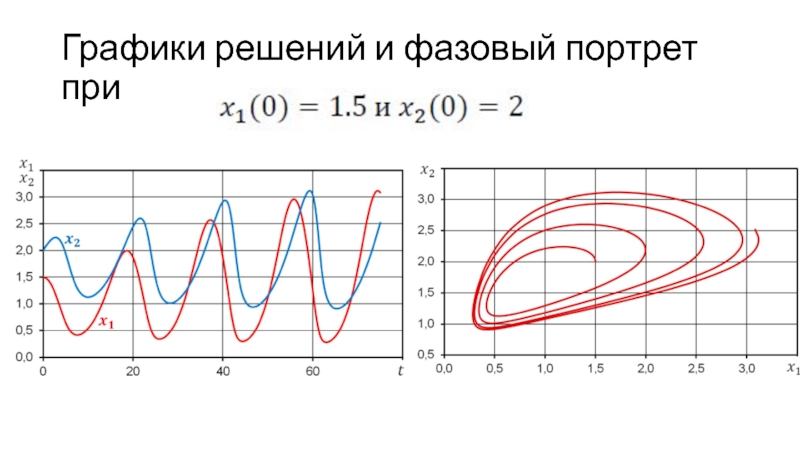
- 34. Графики решений и фазовый портрет при
- 35. Графики решений и фазовый портрет при
- 36. Обобщенная модель взаимодействия двух видов А. Н. Колмогорова
- 37. Обобщенная модель взаимодействия двух видов А. Н.
- 38. Обобщенная модель взаимодействия двух видов А. Н.
- 39. Обобщенная модель взаимодействия двух видов Розенцвейга-МакАртураf(x) –
- 40. Скачать презентанцию
Средства и методы моделированияМетоды моделирования – методы динамической теории системСредства – дифференциальные и разностные уравнения, методы качественной теории дифференциальных уравнений, компьютерная симуляция
Слайды и текст этой презентации
Слайд 2Средства и методы моделирования
Методы моделирования – методы динамической теории систем
Средства
Слайд 3Пример. Рост колонии микроорганизмов
За время прирост численности
равен
,где R – число родившихся и S – число умерших за время особей пропорциональные этому промежутку времени:
В дискретной форме:
В непрерывной форме:
Слайд 4Пример. Рост колонии микроорганизмов
В простейшем случае, когда рождаемость и смертность
пропорциональны численности:
или
Получим экспоненциальную форму динамики роста
Слайд 5Пример. Рост колонии микроорганизмов
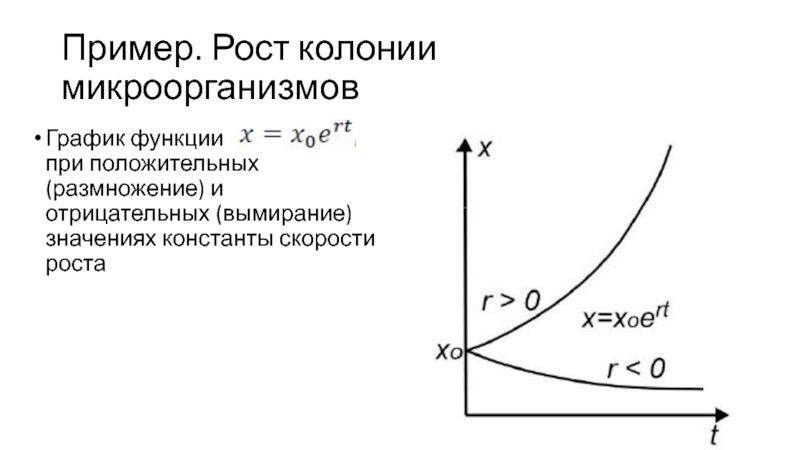
График функции
при положительных (размножение) и отрицательных (вымирание) значениях константы скорости роста
Слайд 6Уравнение Ферхюльста
Логистическое уравнение было предложено Ферхюльстом в 1838 г.
При малых
х численность x возрастает, при больших – приближается к определенному
пределу K.Аналитическое решение имеет вид:
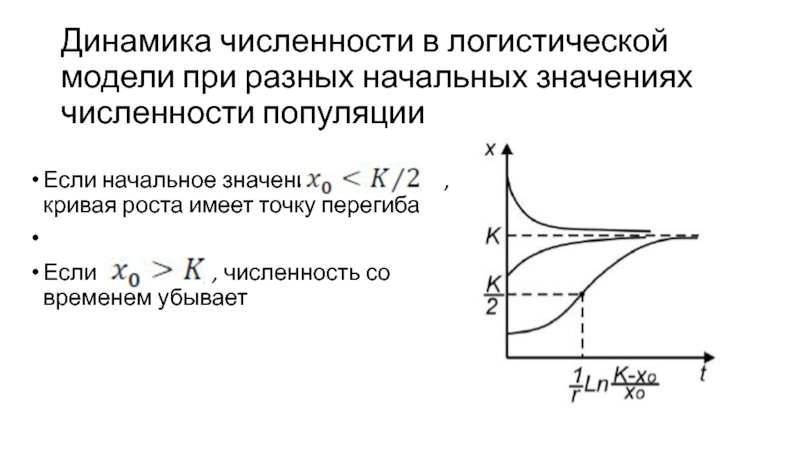
Слайд 7Динамика численности в логистической модели при разных начальных значениях численности
популяции
Если начальное значение
, кривая роста имеет точку перегибаЕсли , численность со временем убывает
Слайд 8Системы двух автономных
дифференциальных уравнений
Рассмотрим систему двух автономных дифф.
Уравнений
P(x, y), Q(x, y) - непрерывные функции, определенные в некоторой
области евклидовой плоскости G (x, y – декартовы координаты) и имеющие в этой области непрерывные производные порядка не ниже первогоx, y – численность видов
Слайд 9Фазовая плоскость
Плоскость всех точек M(x,y) называется фазовой плоскости и изображает
совокупность всех состояний системы.
Точка M(x,y) называется изображающей или представляющей
точкой Совокупность точек M(x(t), y(t)) на фазовой плоскости, положение которых соответствует состояниям системы в процессе изменения во времени переменных x(t), y(t) согласно уравнениям системы, называется фазовой траекторией
Слайд 10Фазовый портрет
Совокупность фазовых траекторий при различных начальных значениях переменных дает
фазовый портрет системы
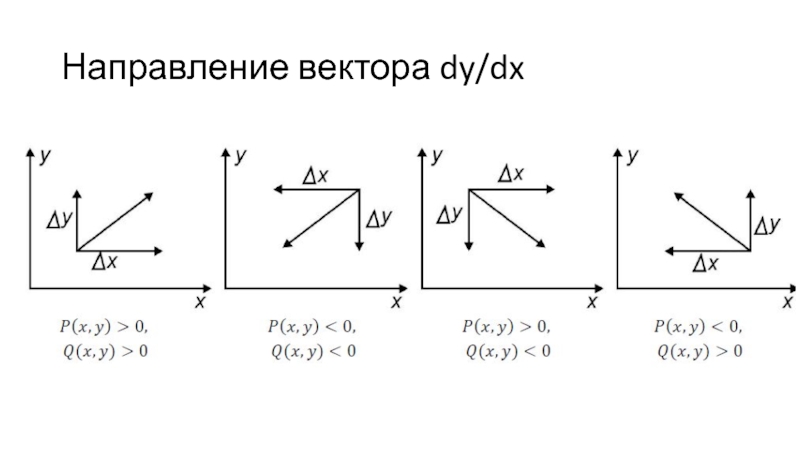
Для изображения фазового портрета необходимо построить векторное поле
направлений траекторий системы в каждой точке фазовой плоскости.Задавая приращение , получим соответствующие приращения
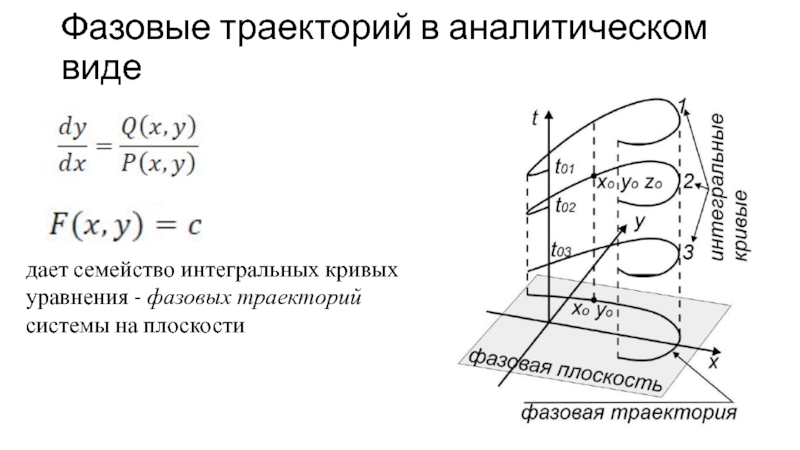
Слайд 12Фазовые траекторий в аналитическом виде
дает семейство интегральных кривых уравнения -
фазовых траекторий системы на плоскости
Слайд 15Математические модели взаимодействия двух видов. Гипотезы Вольтерра
1. Пища либо имеется
в неограниченном количестве, либо ее поступление с течением времени жестко
регламентировано.2. Особи каждого вида отмирают так, что в единицу времени погибает постоянная доля существующих особей.
3. Хищные виды поедают жертв, причем в единицу времени количество съеденных жертв всегда пропорционально вероятности встречи особей этих двух видов, т.е. произведению количества хищников на количество жертв.
Слайд 16Математические модели взаимодействия двух видов. Гипотезы Вольтерра
4. Если имеется пища
в ограниченном количестве и несколько видов, которые способны ее потреблять,
то доля пищи, потребляемой видом в единицу времени, пропорциональна количеству особей этого вида, взятому с некоторым коэффициентом, зависящим от вида (модели межвидовой конкуренции).5. Если вид питается пищей, имеющейся в неограниченном количестве, прирост численности вида в единицу времени пропорционален численности вида.
6. Если вид питается пищей, имеющейся в ограниченном количестве, то его размножение регулируется скоростью потребления пищи, т.е. за единицу времени прирост пропорционален количеству съеденной пищи.
Слайд 17Уравнения Вольтерра
x1, x2 – численности видов
ai – константы собственной скорости
роста видов,
ci – константы самоограничения численности (внутривидовой конкуренции),
bij
– константы взаимодействия видов, (i,j=1,2) Знаки этих коэффициентов определяют тип взаимодействия
Слайд 22Расположение главных изоклин на фазовом портрете
Выживание x1
Выживание x2
Сосуществование видов
Триггерная система
Слайд 25Расположение главных изоклин на фазовом портрете
Устойчивое сосуществование
Популяция хищников вымерла
Точки
1 и 3 неустойчивые
Слайд 26Моделирование динамики популяций с помощью уравнений Лотка-Вольтерра
Модель взаимодействия хищников и
их добычи, когда между особями одного вида нет соперничества
x1
– число жертв, x2 – число хищниковa – скорость размножения жертв в отсутствие хищников,
–bx2 – потери от хищников
–c – относительная скорость изменения популяции хищников
Слайд 28Уравнения Лотка-Вольтерра с логистической поправкой
Модель конкурирующих видов с логистической поправкой
Слайд 31Модель Холлинга-Тэннера
Скорость роста популяции жертв dx1⁄dt в этой модели равна
сумме трех величин
Слайд 32Модель Холлинга-Тэннера
Скорость роста популяции хищников dx2⁄dt строится так же, как
в модели Вольтерра–Лотка, в предположении, что жертвы встречаются редко
Если для
поддержания жизни одного хищника нужно J жертв, то популяция из жертв сможет обеспечить пищей x1/J хищников. Модель роста популяции хищников, в которой их число не может превысить эту критическую величинуСлайд 37Обобщенная модель взаимодействия двух видов А. Н. Колмогорова
1) Хищники не
взаимодействуют друг с другом, т.е. коэффициент размножения хищников k2 и
число жертв L, истребляемых в единицу времени одним хищником, не зависит от y.2) Прирост числа жертв при наличии хищников равен приросту в отсутствие хищников минус число жертв, истребляемых хищниками. Функции k1(x), k2(x), L(x) – непрерывны и определены на положительной полуоси x, y ≥0.
3) Число жертв, истребляемых одним хищником в единицу времени L(x)>0 при x>0; L(0)=0.
Слайд 38Обобщенная модель взаимодействия двух видов А. Н. Колмогорова
4) dk1/dx
0. Это означает, что коэффициент размножения жертв в отсутствие хищника
монотонно убывает с возрастанием численности жертв, что отражает ограниченность пищевых и иных ресурсов.5) dk2/dx > 0, k1(0) < 0 < k1(∞). С ростом численности жертв коэффициент размножения хищников монотонно возрастает, переходя от отрицательных значений, когда нечего есть, к положительным.
Слайд 39Обобщенная модель взаимодействия двух видов Розенцвейга-МакАртура
f(x) – скорость изменения численности
жертв x в отсутствие хищников,
Ф(x,y) – интенсивность хищничества,
k
– коэффициент, характеризующий эффективность переработки биомассы жертвы в биомассу хищника, e – смертность хищника