Слайд 1Моделирование технологических процессов
Лекция 11-12
Слайд 2Методы моделирования процесса термического окисления
Слайд 3Основные процессы, учитываемые при численном моделировании окисления
Точное моделирование окисления
и других термических операций, которые изменяют состав и структуру слоев
должно включать моделирование следующих процессов:
химические реакции на границах раздела слоев, состоящие из растворения частиц,
реакции частиц с материалом слоя,
образование нового слоя;
Слайд 4Основные процессы, учитываемые при численном моделировании окисления
сегрегация примеси на
границах раздела слоев;
диффузия примеси;
Слайд 5Основные процессы, учитываемые при численном моделировании окисления
экранирование потоков
частиц слоями и границами раздела;
механическая деформация слоевой структуры как
результат протекания химических реакций.
Слайд 6- решение уравнения растворения – диффузии – химической реакции для
частиц окислителя,
т.е. расчет процесса диффузии частиц окислителя с граничными
условиями на границах раздела в виде уравнений химических реакций/растворения;
Расчет окислительного процесса
Слайд 7- оценка скоростей образования и поглощения на границе раздела и
определение граничных условий для расчета механических напряжений;
- расчет механических напряжений;
Расчет
окислительного процесса
Слайд 8- вычисление граничных условий и решение уравнения диффузии примеси;
- расчет
изменения толщин слоев;
локальное обновление сетки в окрестности движущихся границ раздела,
интерполяция концентраций,
если необходимо, полное обновление сетки.
Расчет окислительного процесса
Слайд 9Модель Массуда
Позволяет с более высокой точностью моделировать ускоренный начальный
этап окисления за счет введения дополнительных параметров С и τ,
определяющих начальный этап роста окисла
Слайд 10Моделирование окисления в программе DIOS.
Используются два окислительных реагента –
кислород и пары воды.
Основной моделью, устанавливаемой по умолчанию при
расчете скорости роста окисла в одномерном случае, является модель Массуда
Константы А, В, С, τ определяются в зависимости от парциального давления окислительных реагентов, в общем случае для смешанной окислительной атмосферы произвольного состава
Слайд 11В = ВО2 + ВН2О
ВО2 = FP∙RPO2∙pO2
ВH2О =
FP∙RPH2O∙pH2O
RP и RL – константы параболического и линейного роста,
FP и FL – коэффициенты ускорения окисления в сильнолегированных слоях
Слайд 13Пример описания термической операции на входном языке DIOS
Состав атмосферы
можно задавать как сумму потоков каждого компонента FLOW (л/мин), в
этом случае при расчете парциального давления и констант А, В, С, τ принимается во внимание только их соотношение
diff (temp=750, time=30min, atmo=n2)
diff (temp=750, time=10min, flow(N2=9.5l/min, O2=0.5l/min))
diff (temp=(750,950),time=25min, flow(N2=9.5l/min, O2=0.5l/min))
Слайд 14Расчет защищенных маскирующими слоями участков кристалла
diff (temp=750, time=30min, atmo=n2)
diff
(temp=750, time=10min, atmo=n2)
diff (temp=(750,950),time=25min, atmo=n2)
Слайд 15Двумерное моделирование процесса окисления
. Очень часто требуется провести окисление рельефной
поверхности
окисление отдельного участка подложки, не защищенного маской (локальное окисление).
В качестве маски при окислении используется нитрид кремния Si3N4, коэффициент диффузии кислорода в котором очень мал.
В подобных случаях окисление является существенно неодномерным.
Слайд 16Моделирование локального окисления.
Аналитические модели.
L(y,t) – одномерная толщина окисла
в любой точке y, L0 – начальная толщина буферного слоя,
L(t) – толщина окисла вне нитридной маски, определяемая по закону Дила – Гроува, γ – параметр бокового распространения окисла под маской
функция ошибок
Слайд 17Составляющие численных моделей неодномерного роста окисла
исходная модель одномерного окисления (Массуда
или Дила-Гроува);
учет вязкоупругих свойств материалов;
моделирование перемещения межфазной границы в
пространстве;
решение уравнения диффузии в присутствии движущихся границ
Слайд 18Учет вязкоупругих свойств материалов. Вязкая модель.
При температурах окисления выше 950˚С
окисел можно рассматривать как вязкую жидкость. Тогда движение его границ
определяется процессом вязкого течения согласно уравнению
плотность и вязкость стекла, v – скорость движения элементов, p – давление, f – гравитационная сила.
Слайд 19Учет вязкоупругих свойств материалов. Вязкая модель.
Большая вязкость и относительно малая
скорость роста (v< 1 нм/с) позволяют пренебречь в этом уравнении
гравитационным и ускоряющим членами.
Тогда имеем уравнение Навье – Стокса, где вязкая сила уравновешивается градиентом давления
Слайд 20Учет вязкоупругих свойств материалов. Вязкая модель.
В предположении, что окисел можно
считать несжимаемой жидкостью, то уравнение непрерывности потока для вязкого течения
несжимаемой жидкости имеет вид
Если окисел нельзя считать несжимаемым, необходимо задать соотношение между давлением и плотностью окисла. В программе Dios задается в виде:
где p-давление, ρ0 – равновесная плотность, OZP0, OZP1 – коэффициенты (OZP0= 1атм, OZP1=107атм)
Слайд 21Вязкоупругая модель
Если принимать во внимание упругопластичные свойства окисла и
рассматривать его при температуре окисления как сжимаемую жидкость,
то необходимо
учитывать уравнение, описывающее соотношение между давлением и плотностью,
а также рассчитывать механические напряжения в структуре.
Слайд 22Вязкоупругая модель
В линейной вязкоупругой модели принимается линейная зависимость между
механическим напряжением и тензором деформаций в окисле.
В присутствии механических
напряжений константа скорости реакции окисления и коэффициент диффузии окислителя уменьшаются, это необходимо учесть при решении задачи с учетом механических напряжений
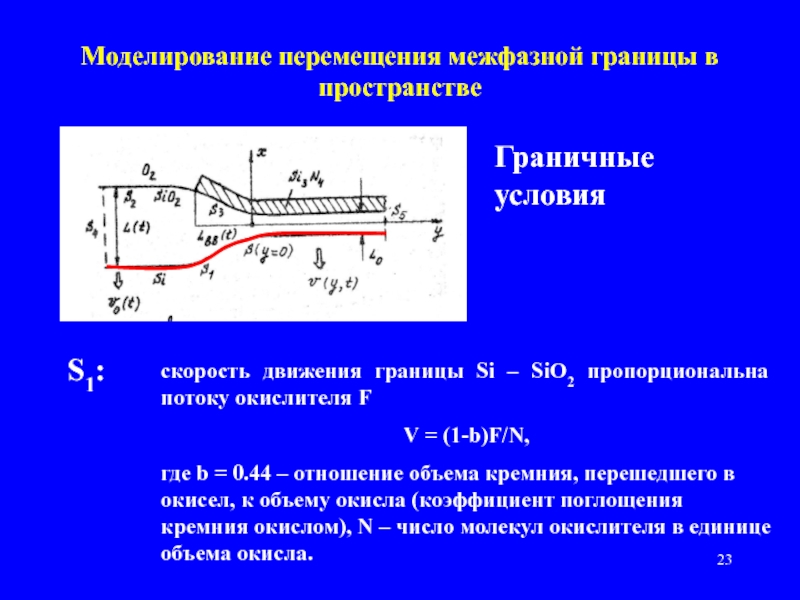
Слайд 23Моделирование перемещения межфазной границы в пространстве
Граничные условия
S1:
скорость движения
границы Si – SiO2 пропорциональна потоку окислителя F
V =
(1-b)F/N,
где b = 0.44 – отношение объема кремния, перешедшего в окисел, к объему окисла (коэффициент поглощения кремния окислом), N – число молекул окислителя в единице объема окисла.
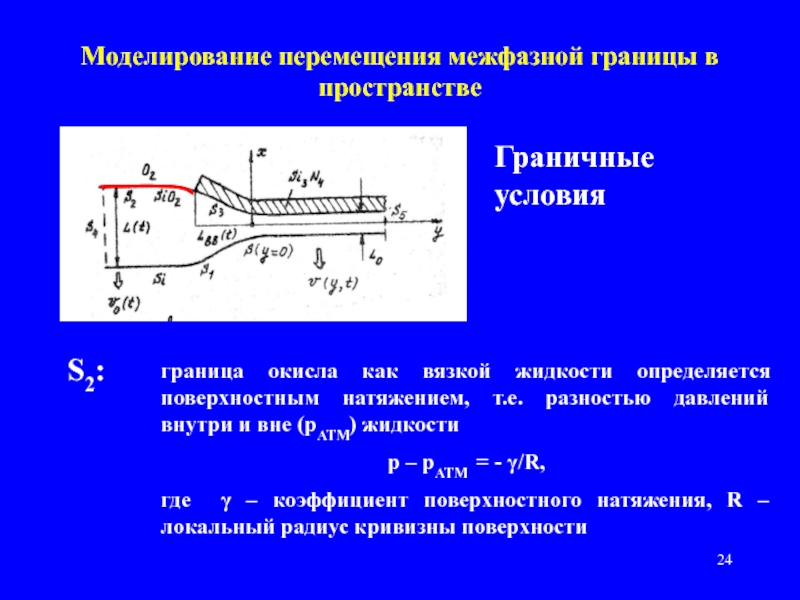
Слайд 24Моделирование перемещения межфазной границы в пространстве
Граничные условия
S2:
граница окисла
как вязкой жидкости определяется поверхностным натяжением, т.е. разностью давлений внутри
и вне (рАТМ) жидкости
p – pАТМ = - γ/R,
где γ – коэффициент поверхностного натяжения, R – локальный радиус кривизны поверхности
Слайд 25Моделирование перемещения межфазной границы в пространстве
Граничные условия
S3:
под маской
жидкость не проскальзывает, а прилипает, что выражается условием
единичный вектор, касательный
к поверхности
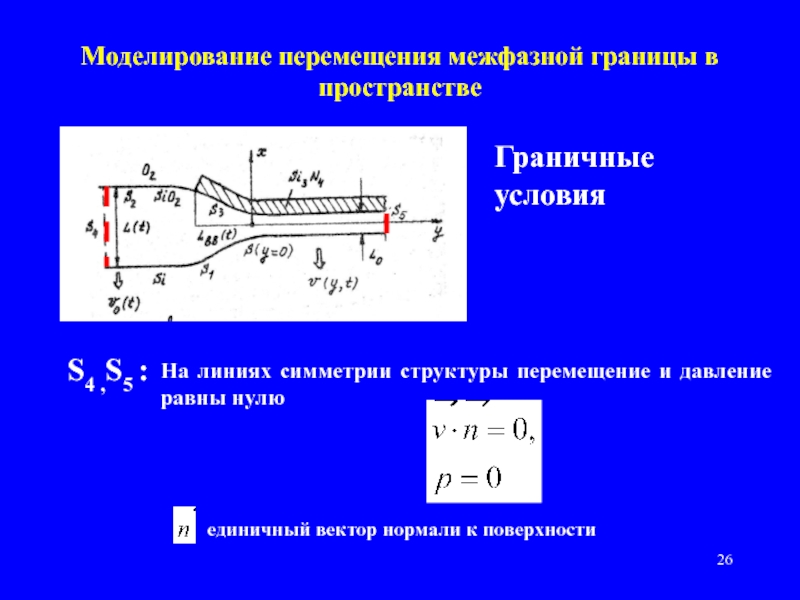
Слайд 26Моделирование перемещения межфазной границы в пространстве
Граничные условия
S4 ,S5
:
На линиях симметрии структуры перемещение и давление равны нулю
единичный
вектор нормали к поверхности
Слайд 27Силицидизация
Один из заключительных этапов формирования транзисторных структур.
Если силицидообразующий металл
и кремний контактируют во время высокотемпературного отжига, идет образования нового
слоя – слоя силицида.
К таким металлам относятся Ti, Ta, Co, W, Pt, Mo.
Взаимодействовать эти металлы могут с кремнием, поликремнием и кремний - германиевыми слоями SiGe.
Процесс силицидизации входит в число структурообразующих операций и моделируется наряду с отжигом и окислением.
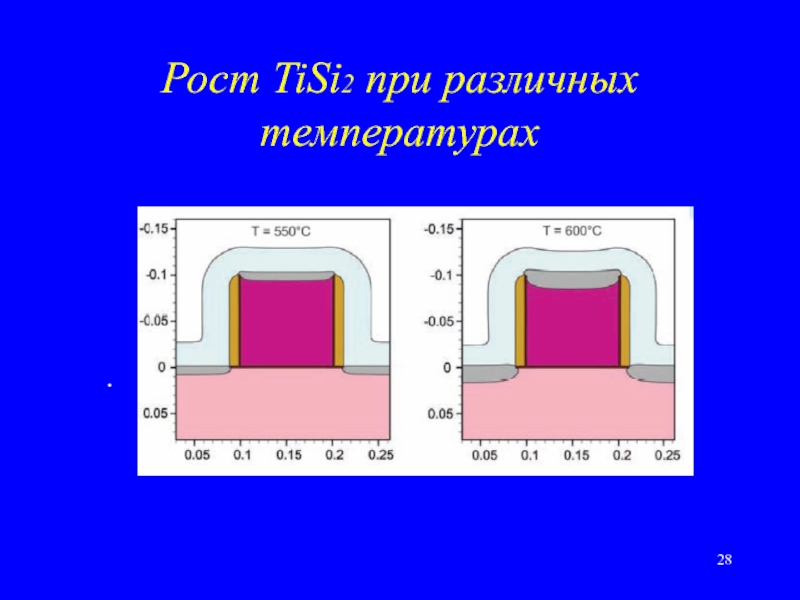
Слайд 28Рост TiSi2 при различных температурах
.
Слайд 29Структура модели силицидизации
Силицидизация с точки зрения моделирования– процесс еще более
сложный, чем окисление.
В окислении участвуют две твердых фазы кремний
и окисел, соответственно, моделируется два слоя переменной толщины.
Считается также, что в процессе окисления диффундируют только частицы окислителя, а диффузией кремния в окисел можно пренебречь.
В процессе силицидизации участвуют три слоя: кремний, силицид и силицидообразующий металл.
При силицидизации кремний является активно диффундирующей компонентой, также, как и металл, и подвижных границ в этой задаче уже не две, а три.
Слайд 30Параметрическая модель силицидизации
Когда высокая точность не обязательна, используется параметрическая модель.
Суть
модели: введение нового слоя силицида в местах протекания реакции металл
– кремний.
Рост силицида не моделируется, а сразу устанавливается его конечная толщина, оцениваемая по модифицированному уравнению Дила – Гроува.
Толщина металла остается неизменной, слой силицида углубляется в кремний.
Модель довольно грубая, бывает полезна, если важен сам факт появления нового слоя с определенными свойствами
Слайд 31Двумерное моделирование силицидизации
Генерация начального слоя силицида (в DIOS начальная толщина
силицида по умолчанию 2 нм) на всех границах, по которым
имеется контакт силицидообразующего металла и кремния в любом виде.
Наиболее точная модель учитывает две составляющие роста силицида:
растворение кремния в силициде, диффузия частиц кремния через силицид к границе с металлом и реакция на этой границе кремния и металла с образованием силицида
растворение металла в силициде, диффузия металла через силицид к границе с кремнием, взаимодействие металла с кремнием на этой границе с образованием силицида.
Слайд 32Расчет составляющих роста силицида
Используется уравнение непрерывности при условии движущихся границ,
включающее сумму диффузионного и конвективного потоков
N – концентрация диффундирующих
частиц (кремния или металла),
диффузионный поток
скорость изменения объема слоя
Слайд 33Расчет составляющих роста силицида
Граничные условия:
- для частиц кремния на границе
кремний – силицид реакция растворения, на границе силицид - металл
- химическая реакция образования силицида;
для частиц металла – реакции растворения и образования силицида меняются местами (границами)
Для точного моделирования необходимо также учитывать возникающие в структуре механические напряжения