Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Molecular Physics. Statistics Lecture 0 8 Probability theory. Probability
Содержание
- 1. Molecular Physics. Statistics Lecture 0 8 Probability theory. Probability
- 2. Thermodynamics and Physical StatisticsThermodynamic Approach- defines correlations
- 3. Statistical Approach- Based on certain models
- 4. Thermodynamics and Physical StatisticsStatistical approach strongly complements
- 5. Probability = the quantitative measure of possibility
- 6. Probability = he quantitative measure of possibility
- 7. EXAMPLE 3. Rotating of a top toy.
- 8. Distribution of ProbabilitiesXφSO: the PROBABILITY for the
- 9. Even Distribution on the PlaneEXAMPLE 4: a
- 10. Even Distribution in PhysicsEXAMPLE 5: Molecules in
- 11. THE PROPERTIES OF AVERAGES. Average of the
- 12. Probability Distribution and Average ValuesExamples: in case
- 13. Different Kinds of AveragesYXZV = = 3R/4
- 14. Eagle and Tails gameNormal Distribution
- 15. Eagles and Tails GameEXAMPLE 1: One throw
- 16. EXAMPLE 2: 1 Test (or one series
- 17. The product of probabilities: The first test
- 18. General Case: The test length = N
- 19. The test series has the length N
- 20. BAR CHARTSmooth CHART – distribution functionx x+aΔPx SOME MATHEMATICS: the probability distribution
- 21. N – number pf tests, Ni –
- 22. Normal distributionThe normal (or Gauss) distribution –
- 23. Gauss DistributionThe normal distribution is very often
- 24. Normal (Gauss) Distribution and EntropyMEPhI General Physics
- 25. Number of variants leasing to the result
- 26. The Entropy of ProbabilityThe definition of the
- 27. Entropy in InformaticsType of result Realizationsk = 0 0000000000
- 28. Entropy in InformaticsAny information or communication can
- 29. The deffinition of entropy as the measure
- 30. Statistical Entropy in PhysicsMEPhI General Physics
- 31. Distribution of Molecules over possible “micro-states” Imagine
- 32. Statistical Entropy in Molecular Physics: the logarithm
- 33. Слайд 33
- 34. Not a strict proof, but plausible considerations.
- 35. Statistical Entropy and the Entropy of Ideal
- 36. 2nd Law of Thermodynamics and the ‘Time
- 37. The Distributions of Molecules over Velocities and
- 38. Thank You for Attention!
- 39. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Molecular Physics. Statistics
Lecture 08
Probability theory.
Probability Distributions
Statistical Entropy
MEPhI General
Physics
Слайд 2Thermodynamics and Physical Statistics
Thermodynamic Approach
- defines correlations between the observed
physical quantities (macroscopic),
relies mostly on the experimentally established dependencies
allows
generally to consider the physical essence of the problem -does not require precise information about the microscopic structure of matter.
Слайд 3Statistical Approach
- Based on certain models of the micro-structure
of matter
defines correlations between the observed physical quantities, starting from
the laws of motion of molecules using the methods of probability theory and mathematical statisticsallows to understand the random fluctuations of macroscopic parameters.
Thermodynamics and Physical Statistics
Thermodynamic Approach
- defines correlations between the observed physical quantities (macroscopic),
relies mostly on the experimentally established dependencies
allows generally to consider the physical essence of the problem -
does not require precise information about the microscopic structure of matter.
Слайд 4Thermodynamics and Physical Statistics
Statistical approach strongly complements thermodynamics. BUT! To
implement it effectively we need proper mathematical tools – first
of all – the probability theory.This will be the focus of today’s lecture!…
Thermodynamic Approach
- defines correlations between the observed physical quantities (macroscopic),
relies mostly on the experimentally established dependencies
allows generally to consider the physical essence of the problem -
does not require precise information about the microscopic structure of matter.
Statistical Approach
- Based on certain models of the micro-structure of matter
defines correlations between the observed physical quantities, starting from the laws of motion of molecules using the methods of probability theory and mathematical statistics
allows to understand the random fluctuations of macroscopic parameters.
Слайд 5Probability = the quantitative measure of possibility for certain event
to occur.
EXAMPLE 1. Eagle and Tails Game:
Test = throw of
a coin; Results of a test (events); eagle. or tail
If the game is honest – possibilities to obtain each result must be equal.
Quantitative measure of possibility = probability: Pe=0,5 – eagle; Pt=0,5 - tail.
P = 1 is the probability of a “valid” event, which will occur for sure.
Pe + Pt=1 – either eagle or tail will fall out for sure (if rib is excluded ).
The rule of adding probabilities P (1 OR 2) = P(1) + P(2)
The normalization rule: the sum of probabilities for all possible results of a test is evidently valid and thus is equal to 1.
Probabilities
Слайд 6Probability = he quantitative measure of possibility for certain event
to occur.
EXAMPLE 2. Dice game. Test = throw of a
dice; Results of a test (events); 1, 2, 3, 4, 5, 6
If the game is “honest”: P(1) = P(2) = P(3) = P(4) = P(5) = P(6) = 1/6.
Example 2.1: Probability to obtain the odd number as the result of a test:
P(1) + P(3) + P(5) = 1/6 + 1/6 + 1/6 = 1/2
Example 2.2: Probability to obtain “double 6”: from the first throw P(6) = 1/6, and then – out of this probability only 1/6 of chances that 6 will occur again. Finally P( 6 AND 6) = P(6)P(6) = 1/6*1/6 = 1/36
The rule of multiplying probabilities P (1 AND 2) = P(1)P(2)
Probabilities
Слайд 7EXAMPLE 3. Rotating of a top toy.
If initially the
red mark was exactly to the right from the top
toy’s axis (in direction X), after rotation stops - it may stop at any angle .The question: what is the probability that the toy wil stop EXACTLY turned by the angle φ from the initial orientation? The answer: P(φ) = 0 (!) – as absolutely precise experiments are impossible in principle. There always will be some error, or deviation, or uncertainty.
Distribution of Probabilities
X
φ
The CORRECT question: what is the probability for the top toy to stop within certain range of angles: between φ and (φ + dφ)?
Evidently, this probability MAY depend on φ and MUST be proportional to dφ:
dP(φ to φ + dφ) = f(φ)dφ
Here f(φ) is the probability distribution function.
Слайд 8Distribution of Probabilities
X
φ
SO: the PROBABILITY for the top toy to
stop between φ and (φ + dφ) equals: dP(φ to
φ + dφ) = f(φ)dφf(φ) is the probability distribution function.
The Normalization Rule: the integration of the probability distribution function over the range of all possible results MUST give 1
In our example: 2π∫0 f(φ)dφ = 1
The Even Distribution: if all possible results are equally probable – the distribution function equals constant.
In our example: f(φ) = Const = 1/ 2π
Слайд 9Even Distribution on the Plane
EXAMPLE 4: a point is dropped
(randomly) on the table with the area S. What is
the probability that it will fall within the little square within dS?f(x,y) = C: the even probability distribution function.
The Normalization Rule: ∫S Cdxdy = CS = 1 => C = 1/S
The result: dP(dS) = f(x,y)dS = dS/S
dS
S
Слайд 10Even Distribution in Physics
EXAMPLE 5: Molecules in gas – at
the state of thermal equilibrium, when the concentration of molecules
is the same all throw the volume are evenly distributed over all the coordinates:f(x,y,z) = Const = 1/V =
dP(x,y,z) = f(x,y,z)dV = dxdydz/V
dV
V
Слайд 11THE PROPERTIES OF AVERAGES.
Average of the sum of two
values equals to the sum of their averages
= Average of the product of two values equals to the product of their averages ONLY in case if those two values DO NOT depend on each other
Probability Distribution and Average Values
Knowing the distribution of a random x we may calculate its average value Moreover, we may calculate the average for any function ψ(x):
Слайд 12Probability Distribution and Average Values
Examples: in case of even distribution
of molecules over certain spherical volume V (balloon with radius
R):Y
X
Z
V
= 0
Calculation – ‘live”…
Слайд 13Different Kinds of Averages
Y
X
Z
V
= = 3R/4
- average
()1/2 = 0,61/2R > - squared average
=
0; Median average rmed ; the quantity of molecules with r
rmed=R/21/3=0,7937R >
(
This all is about even distribution of molecules over space in spherical balloon.
What about the distribution of molecules over velocities and energies?
It can be spherically symmetric, but it can not be even as formally there is no upper limit of velocity…
Слайд 15Eagles and Tails Game
EXAMPLE 1: One throw of a coin
= one Test (N = 1)
Test Results: type 1 –
“Tail”; type 0 – “Eagle”If we do very many tests (throws)
= 0,5 both for types 1 and 0.
NT – number of tests (throws),
Ni – number of tests with the result of the type i
Рi – probability to obtain the result of the type i
T
Слайд 16EXAMPLE 2: 1 Test (or one series of tests) =
2 throws of a coin (N = 2)
Test results
(types): 0 –2 Eagles
1 –1 Eagle and 1 Tail or
2 –2 Tails
= 0,25 probability of types 0 and 2
= 0,5 – probability of type 1
N – the length of a test series (in this case N = 2) ,
NT – total number of tests
Ni – number of tests with result of the type i
Рi – probability to obtain the result of the type i
T
Eagles and Tails Game
Слайд 17
The product of probabilities:
The first test – the probability
of result “1” - P1
The second test – the probability
of result “2” = P2.The probability to obtain the result ‘1’ at first attempt and then to obtain result ‘2’ at second attempt equals to the product of probabilities
P(1 AND 2) = P(1 ∩ 2) = P1P2
EXAMPLE: Eagle AND Tail = ½ * ½ = ¼
The SUM of probabilities:
One test – the probability of result “1” - P1; the probability of result “2” = P2.
The probability to obtain the result ‘1’ OR ‘2’ equals to the SUM of probabilities: P(1 OR 2) = P(1 U 2) = P1 + P2
EXAMPLE: Eagle OR Tail = ½ + ½ = 1
EXAMPLE 2: (Eagle AND Tail) OR (Tail AND Eagle) = ¼ + ¼ = ½
T
SOME MATHEMATICS
Слайд 18General Case: The test length = N (N throws =
1 test)
All the types of test results can be
numbered i from 0 to N by the number of the tailspins in each test. Each type of results will have the probability, proportional to the number of variants, that produce that resultType Number of variants producing this type of result
i = 0 1 (all the throws = eaglespins)
i = 1 N (only one there was a tailspin (either at first throw, or at the 2nd, or at the 3rd, … or at the last)
i = 2 N(N -1)/2
i = 3 N(N-1)(N-2)/6
…..
i = k N(N-1)(N-2)….(N-k+1)/k! = N!/k!(N-k)!
….
i = N-1 N
i = N 1 (all the throws = tailspins)
Eagles and Tails Game
Слайд 19The test series has the length N (N throws =
attempts)
Number of variants to obtain the result of the type
k (with k tailspins):Ωk= N!/k!(N-k)!
ΣΩk= 2N
Probability to obtain the result of the type k:
Pk= N!/k!(N-k)!2N
If N>>1 we may apply the Sterling's approximation:
ln(n!) ~= n ln(n/e)
Для N = 10
Pk= (2/πN)1/2exp(-2(k-N/2)2/N)
here n = (k - N/2) – is the deviation of the obtained result from the average N/2. Probabilities are noticeable when n<~N1/2 << N
Eagles and Tails Game
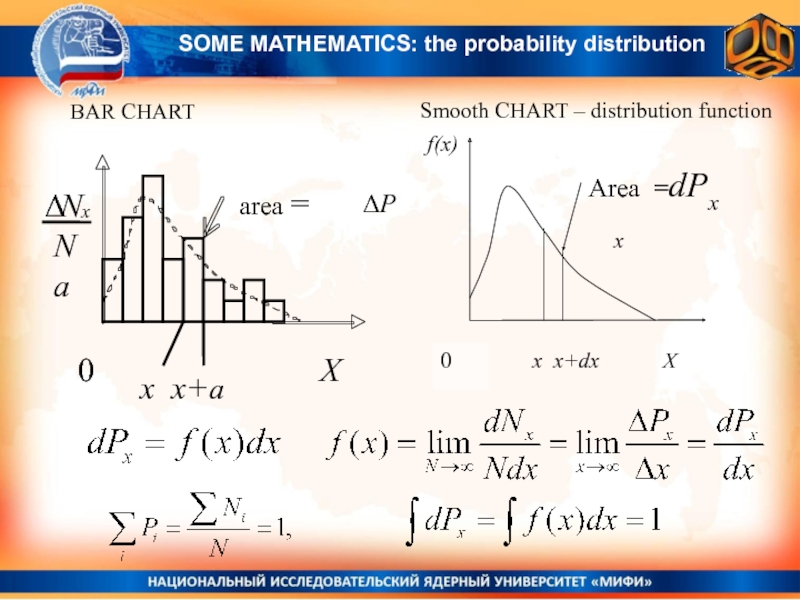
Слайд 20BAR CHART
Smooth CHART – distribution function
x x+a
ΔP
x
SOME MATHEMATICS: the
probability distribution
Слайд 21N – number pf tests,
Ni – number of results
of the type i
Рi – probability of the result
of the type i SOME MATHEMATICS
For continuously distributed quantities X:
differential probability to find the random value X within the range from X to X + dX dP(x) = f(x)dx
f(x) – is the probability distribution function
Probability to find the random value X within the range from x1 to x2 :
For continuously distributed quantities the probability to have exactly some value x0, is equal to zero P(x = x0)=0.
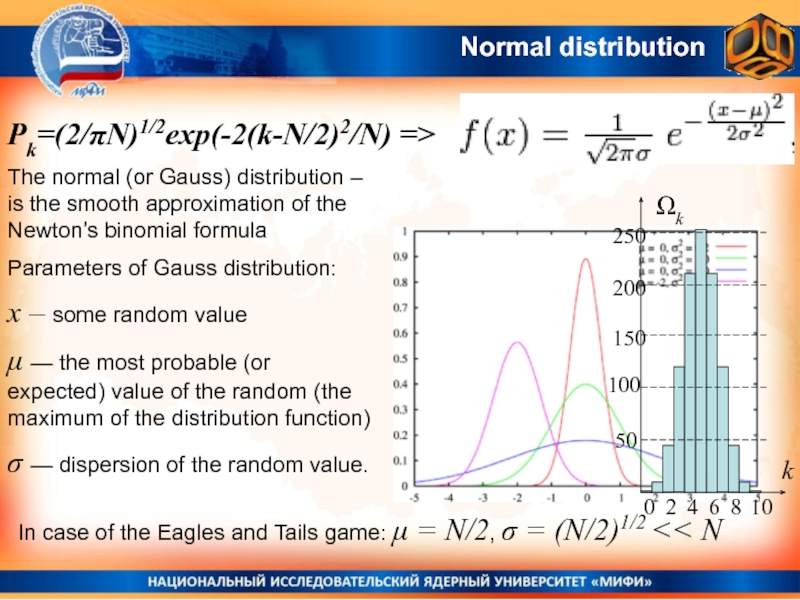
Слайд 22Normal distribution
The normal (or Gauss) distribution – is the smooth
approximation of the Newton’s binomial formula
Parameters of Gauss distribution:
x –
some random valueμ — the most probable (or expected) value of the random (the maximum of the distribution function)
σ — dispersion of the random value.
In case of the Eagles and Tails game: μ = N/2, σ = (N/2)1/2 << N
Pk=(2/πN)1/2exp(-2(k-N/2)2/N) =>
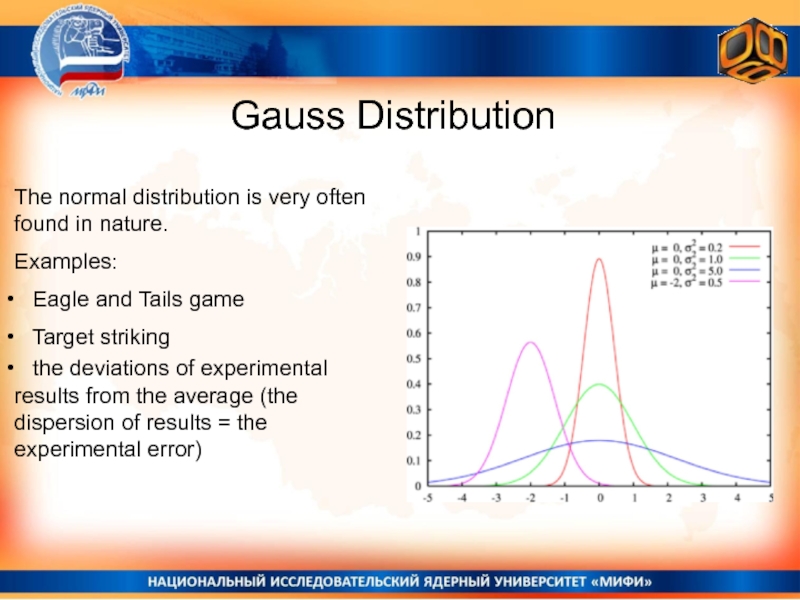
Слайд 23Gauss Distribution
The normal distribution is very often found in nature.
Examples:
Eagle and Tails game
Target striking
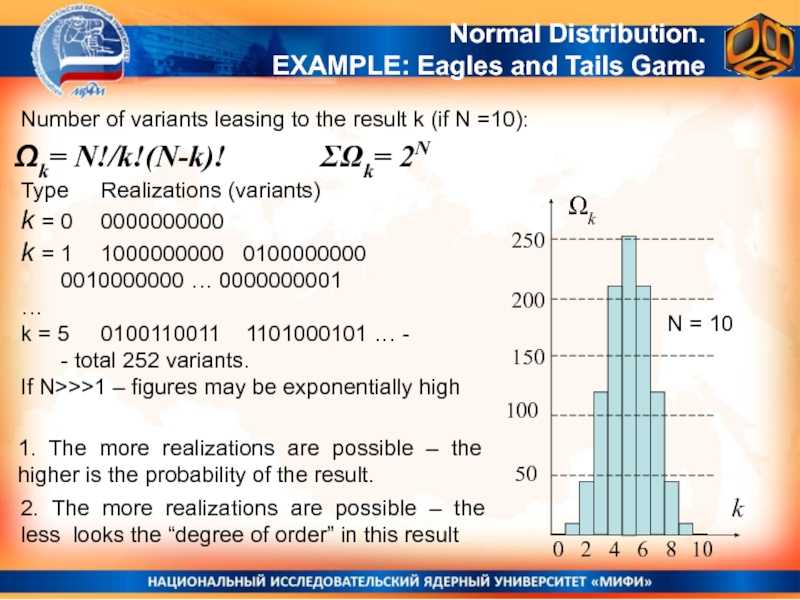
the deviations of experimental results from the average (the dispersion of results = the experimental error)Слайд 25Number of variants leasing to the result k (if N
=10):
Ωk= N!/k!(N-k)!
Normal Distribution.
EXAMPLE: Eagles and Tails Game
ΣΩk= 2N
N = 10
Type Realizations (variants)
k = 0 0000000000
k = 1 1000000000 0100000000
0010000000 … 0000000001
…
k = 5 0100110011 1101000101 … -
- total 252 variants.
If N>>>1 – figures may be exponentially high
1. The more realizations are possible – the higher is the probability of the result.
2. The more realizations are possible – the less looks the “degree of order” in this result
Слайд 26The Entropy of Probability
The definition of the entropy of probability:
S(k) = ln(Ωk) -
N = 10
S(k) = Aln(Pk) =
Aln(Ωk) - ANln2The higher is the “order” – the lower is entropy
The higher is probability – the higher is entropy
P(k и i) = PkPi => S(k и i) = S(k)+S(i)
Entropy is the additive function!
If N = 10
S(0) = S(10) = ln(1) = 0
S(5) = ln(252) = ~5,6
The more realizations are possible – the more is the probability of it and the less is the “degree of order” in this result. For long series of tests (N>>>1) numbers of variants of realizations may be exponentially high and it may be reasonable to apply logarithmic functions)
Слайд 27Entropy in Informatics
Type of result Realizations
k = 0 0000000000
k = 1 1000000000
0100000000 ...
k = 5 0100110011 1101000101 …
Any information
or communication can be coded as a string of zeroes and units: 0110010101110010010101111110001010111…. (binary code)To any binary code with length N (consisting of N digits, k of which are units and (N-k) – are zeroes) we may assign a value of entropy:
S(N,k) = ln(ΩN,k), where ΩN,k – is the number of variants how we may compose a string out of k units and (N-k) zeroes
Communications, looking like 00000000.. 111111111… S = 0
Communications with equal number of units and zeroes have maximal entropy .
Entropy of 2 communications equals to the sum of their entropies.
Слайд 28Entropy in Informatics
Any information or communication can be coded as
a string of zeroes and units: 0110010101110010010101111110001010111…. (binary code)
The entropy
of information or communication, containing k units and (N-k) zeroes is defined like: S(N,k) = ln(ΩN,k), where ΩN,k – is the number of variants how we may compose a string out of k units and (N-k) zeroesCommunications, looking like 00000000.. 111111111… S = 0 … the informational value of such ‘communication’ is also close to zero
Communications with equal number of units and zeroes have maximal entropy . Most probably they are the sets of randomly distributed symbols, thus also having practically no informational value
Entropy of 2 communications equals to the sum of their entropies.
Real informative communications as a rule
do include fragments with noticeable predominance of either zeroes or units, and
Have the entropy noticeably different from both maximum and minimum
Слайд 29The deffinition of entropy as the measure of disorder (or
the measure of informational value) in informatics was first introduced
by Claude Shannon in his article «A Mathematical Theory of Communication», published in Bell System Technical Journal in 1948Those ideas still serve as the base for the theory of connunications, tmethods on encoding and decoding, are used in linguistics etc…
Claude Elwood Shannon
1916 - 2001
Entropy in Informatics
Слайд 31Distribution of Molecules over possible “micro-states”
Imagine that we have
К possible “states” and we have N “molecules” that can
be somehow distributed over those “states”The row of numbers (n1, n2, …nK) = n(i) forms what is called the «macro-state» of the system. Each macro-state can be realized by the tremendously great number of variants Ω(n(i)). The number of variants of realization is called the “statistic weight” of the macro-state.
The more is the “statistic weight” – the greater is the probability to realize this state.
Even distribution of molecules over space has the biggest statistical weight and thus id usually associated with thermo-dynamical equilibrium.
Слайд 32 Statistical Entropy in Molecular Physics: the logarithm of the number
of possible micro-realizations of a state with certain macro-parameters, multiplied
by the Boltzmann constant.In the state of thermodynamic equilibrium, the entropy of a closed system has the maximum possible value (for a given energy).
If the system (with the help of external influence)) is derived from the equilibrium state - its entropy can become smaller. BUT…
If a nonequilibrium system is left to itself - it relaxes into an equilibrium state and its entropy increases
The entropy of an isolated system for any processes does not decrease, i.e. ΔS > 0 , as the spontaneous transitions from more probable (less ordered) to less probable (more ordered) states in molecular systems have negligibly low probability
J/K
Statistical Entropy in Physics.
5. The entropy is the measure of disorder in molecular systems.
Слайд 33
Entropy is the
additive quantity.
J/К
Statistical Entropy in Physics.
For the state of the
molecular system with certain macroscopic parameters we may introduce the definition of Statistical Entropy as the logarithm of the number of possible micro-realizations (the statistical weight of a state Ώ) - of a this state, multiplied by the Boltzmann constant.Слайд 34Not a strict proof, but plausible considerations.
Statistical Entropy and
the Entropy of Ideal Gas
the number of variants
of realization of a state (the statistical weight of a state) shall be higher, if the so called phase volume, available for each molecule (atom), is higher: Phase volume Ω1 ~Vp3~VE3/2 ~VT3/2 As molecules are completely identical, their permutations do not change neither the macro-state, nor the micro-states of the system. Thus we have to reduce the statistical weight of the state by the factor ~ N! (the number of permutations for N molecules)
the phase volume for N molecules shall be raised to the power N:
Ω ~ VNT3N/2.
For multy-atomic molecules, taking into account the possibilities of rotations and oscillations, we shall substitute 3 by i : Ω ~ VNT iN/2
Ω~ VNTiN/2 /N!; S=k ln Ω =kNln(VTi/2/NC)=
= v(Rln(V/v) + cVlnT +s0)
Слайд 35
Statistical Entropy and the Entropy of Ideal Gas
Ω~ VNTiN/2 /N!;
S=k ln Ω =kNln(VTi/2/NC)=
= v(Rln(V/v) + cVlnT +s0)
The statistical entropy proves
to be the same physical quantity, as was earlier defined in thermodynamics without even referring to the molecular structure of matter and heat! Слайд 362nd Law of Thermodynamics and the ‘Time arrow’
“The increase of
disorder, or the increase of the Entropy, of the Universe
over time -is one of the possibilities to define the so-called “Time arrow”, that is the direction of time, or the ability to distinguish the past from the future,
Stephen Hawking
(1942-2018)