Слайд 1Мультимедийные лекции
по физике
Магнетизм
Слайд 2Тема 4. Явление электромагнитной индукции
План лекции
4.1. Явление электромагнитной индукции. Закон
Фарадея.
4.2 ЭДС индукции в движущемся проводнике.
4.3. ЭДС индукции во
вращающемся проводнике.
4.4. Переменная ЭДС индукции. Переменный ток.
4.5. Самоиндукция. Индуктивность соленоида
4.6. Взаимная индукция. Трансформатор.
4.7. Токи при замыкании и размыкании электрических цепей.
4.8. Вихревые токи (токи Фуко).
4.9. Энергия магнитного поля.
Слайд 34.1. Явление электромагнитной индукции. Закон Фарадея.
Электрический ток порождает вокруг себя
магнитное поле.
Способно ли магнитное поле вызывать в окружающем пространстве электрическое
поле?
На этот вопрос ответил М. Фарадей, проделав в 18 веке более 100 опытов, которые можно разбить на 3 отдельные группы.
Слайд 4
Майкл Фа́радей (1791 - 1867) - английский физик, основоположник учения
об электромагнитном поле.
Электромагнитная индукция была открыта Фарадеем в 1831 году.
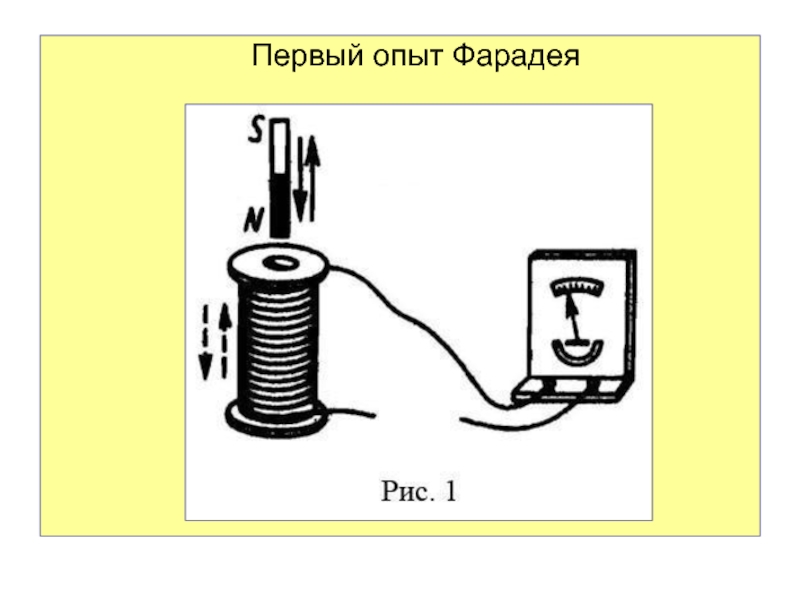
Слайд 5В первой группе опыты сводились к движению постоянного магнита через
плоскость, ограниченную проводящим контуром, в который был включён чувствительный гальванометр.
При
быстром вдвигании или выдвигании магнита его силовые линии пересекали плоскость витка, в последнем появлялся кратковременный ток.
N
S
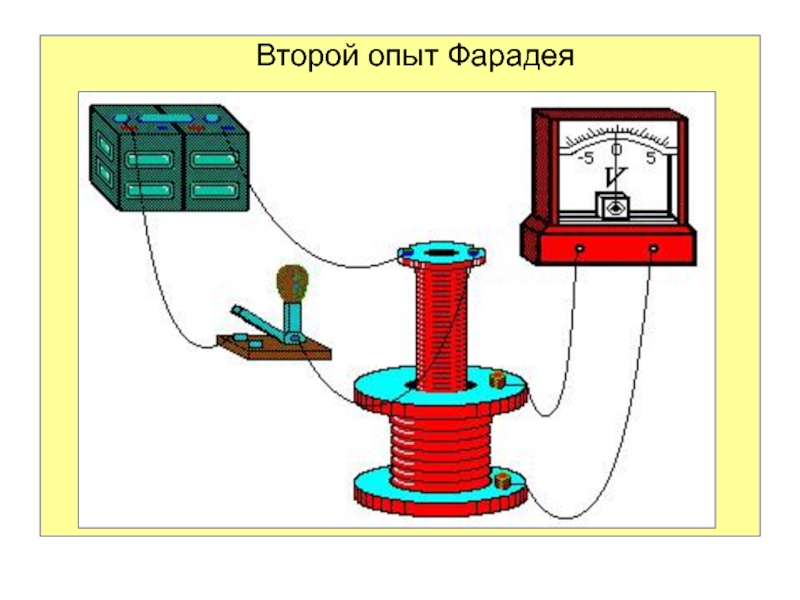
Слайд 72. Во второй группе опытов магнитное поле создавалось в малой
катушке индуктивности (соленоиде).
При быстром вдвигании или выдвигании её в большую
катушку , в последней возникал ток.
3. В третьей группе опытов в проводящем контуре можно было получить ток, если в другом контуре, сцеплённым с первым, протекал переменный ток.
Из всех опытов Фарадея следовало, что магнитное поле порождало в окружающем пространстве электрическое поле.
Слайд 9Электрическое поле можно было обнаружить проводящим контуром, в котором оно
заставляло направленно двигаться заряды (электроны), что приводило к появлению тока,
который называется индукционным.
Появление индукционного тока в первую очередь можно связать с появлением в проводящем контуре ЭДС индукции (по аналогии с ЭДС источника тока).
Явление электромагнитной индукции заключается в появлении ЭДС индукции (индукционного тока) в проводящем контуре при любом изменении магнитного потока через площадь, сцеплённую с этим контуром.
Слайд 10Закон Фарадея: ЭДС индукции прямо пропорциональна скорости изменения магнитного потока.
Знак
минус появляется в связи с правилом Ленца.
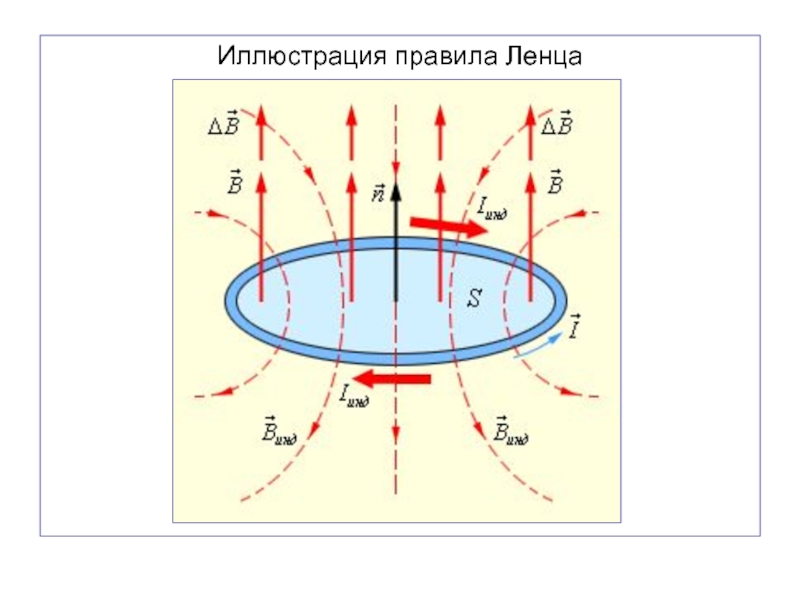
Правило Ленца: индукционный ток
имеет такое направление в проводящем контуре, что своим собственным магнитным полем препятствует любому изменению магнитного потока, который вызвал появление данного индукционного тока.
Слайд 12Физический смысл ЭДС индукции аналогичен смыслу ЭДС источника тока.
Сторонними силами
в явлении электромагнитной индукции являются силы переменного электрического поля или
сила Лоренца.
ЭДС индукции равна работе сил переменного электрического поля по перемещению единичного положительного заряда по проводящему контуру.
Слайд 13ЭДС индукции измеряется в вольтах: [εi] = 1В.
ЭДС индукции может
возникать в двух случаях:
в постоянном магнитном поле должен двигаться проводник,
пересекая его силовые линии.
Роль сторонних сил выполняет сила Лоренца
2. неподвижный контур должен пронизываться непостоянным магнитным полем через площадь, сцеплённую с этим контуром.
Роль сторонних сил выполняют силы переменного магнитного поля.
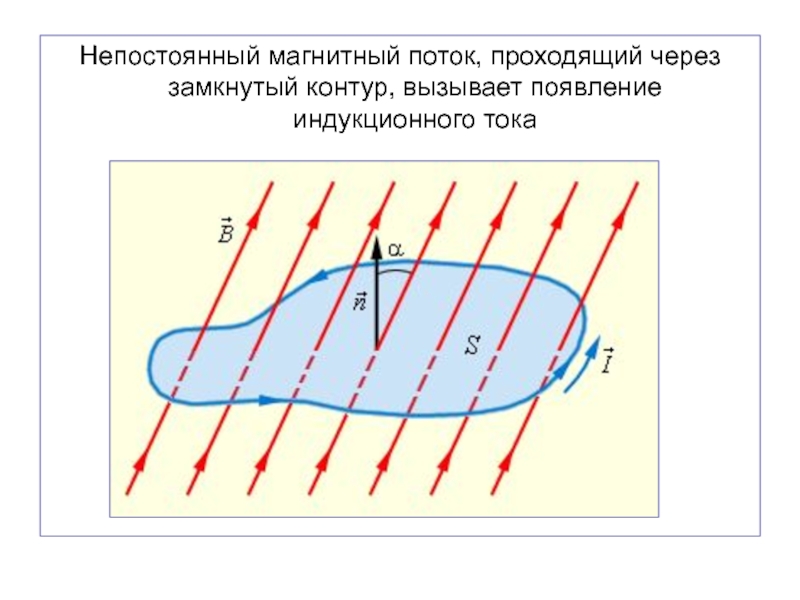
Слайд 14Непостоянный магнитный поток, проходящий через замкнутый контур, вызывает появление индукционного
тока
Слайд 15Сила индукционного тока вычисляется по закону Ома:
Величина индукционного заряда
вычисляется по формуле:
Слайд 16Обратимся к формуле магнитного потока:
Изменение магнитного потока может быть вызвано
разными причинами:
Явление электромагнитной индукции широко при меняется в технике.
Слайд 174.2. ЭДС индукции в движущемся проводнике
Пусть в однородном магнитном поле
равномерно движется металлический проводник перпендикулярно его силовым линиям.
L – длина
проводника;
v – скорость движения;
В – магнитная индукция.
На каждый свободный электрон проводника действует сила Лоренца:
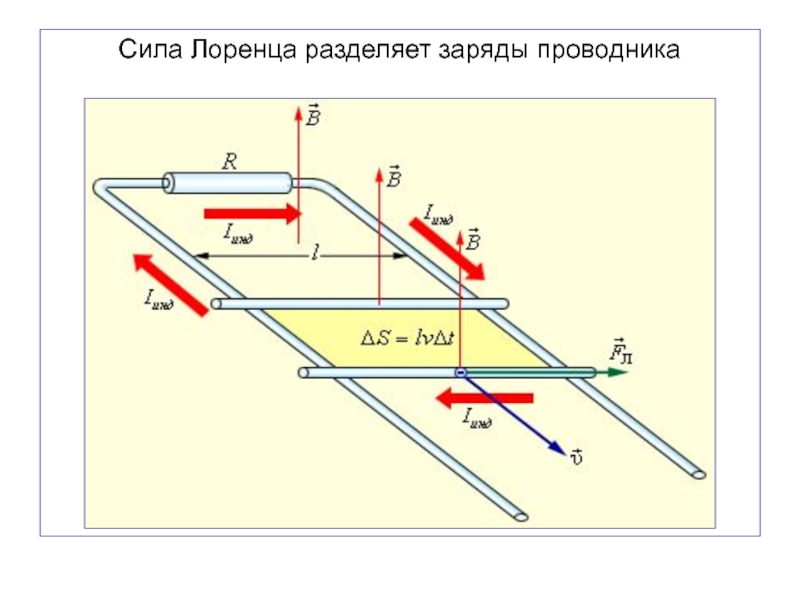
Слайд 18Сила Лоренца разделяет заряды проводника
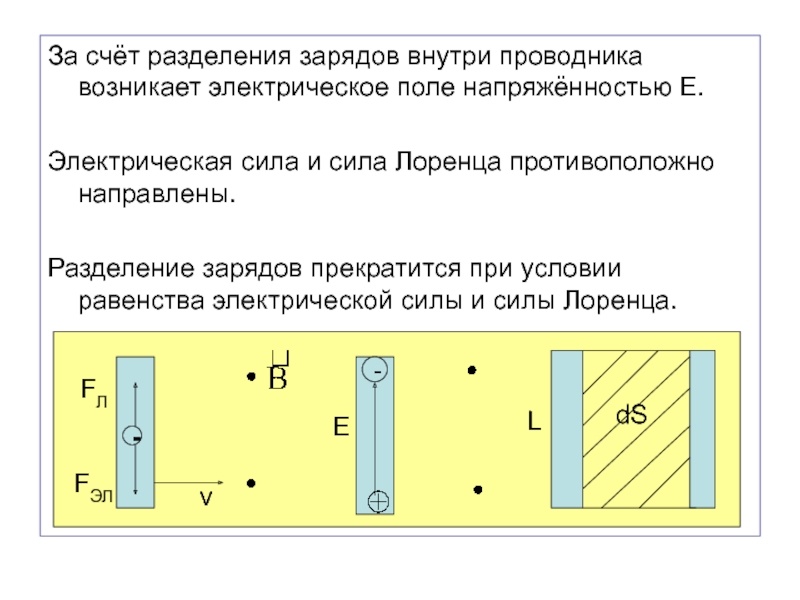
Слайд 19За счёт разделения зарядов внутри проводника возникает электрическое поле напряжённостью
Е.
Электрическая сила и сила Лоренца противоположно направлены.
Разделение зарядов прекратится при
условии равенства электрической силы и силы Лоренца.
-
FЛ
FЭЛ
v
-
E
dS
L
Слайд 20
При движении проводника на его концах образуется постоянная разность потенциалов
U.
Она и будет здесь являться ЭДС индукции.
Слайд 21Аналогичную формулу для ЭДС индукции получим при использовании закона Фарадея.
ЭДС
индукции тем больше, чем больше скорость движения проводника и чем
больше магнитная индукция.
Слайд 22
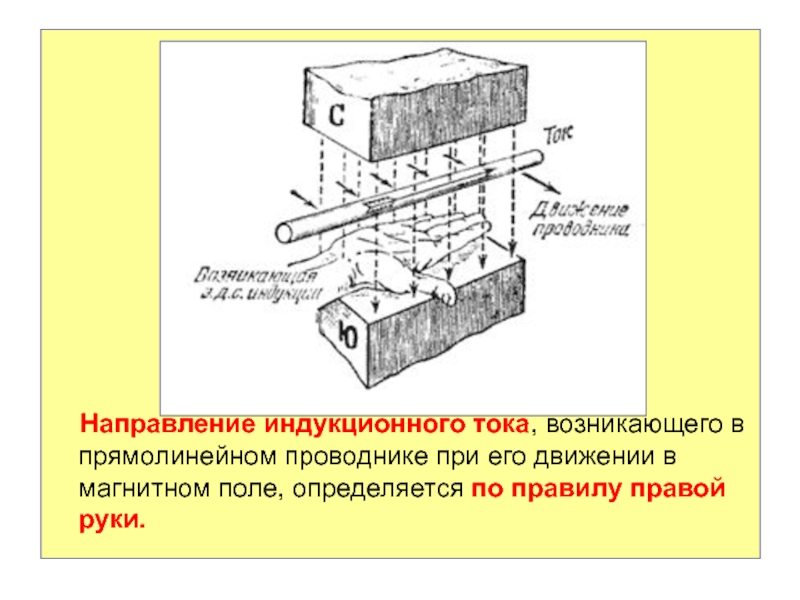
Направление индукционного тока, возникающего в прямолинейном проводнике при его движении
в магнитном поле, определяется по правилу правой руки.
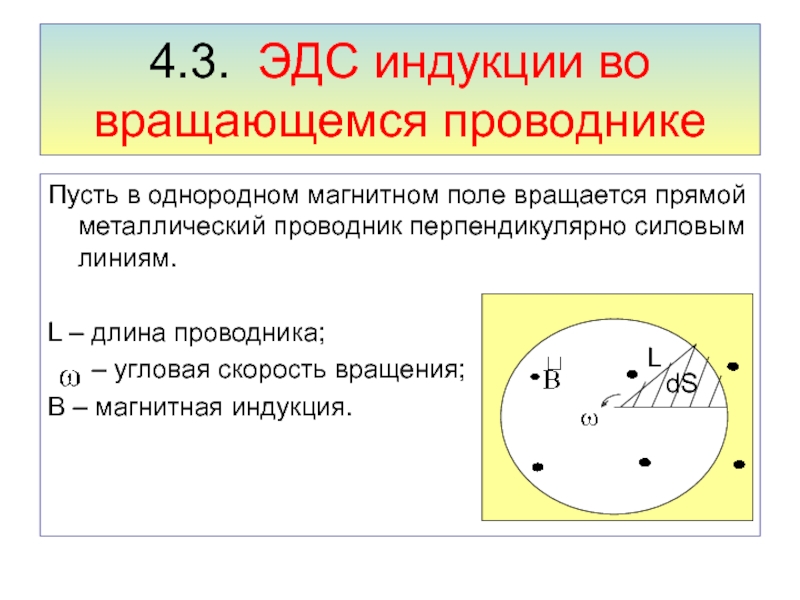
Слайд 234.3. ЭДС индукции во вращающемся проводнике
Пусть в однородном магнитном поле
вращается прямой металлический проводник перпендикулярно силовым линиям.
L – длина проводника;
– угловая скорость вращения;
В – магнитная индукция.
dS
L
Слайд 25ЭДС индукции появляется за счёт действия силы Лоренца, которая, как
и в предыдущем случае, разделяет заряды проводника.
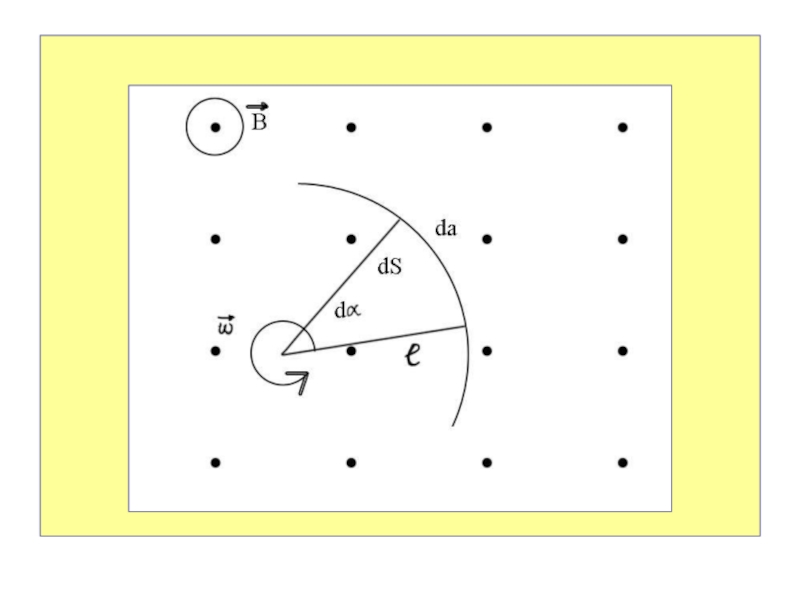
По закону Фарадея:
Площадь dS,
пересекаемую в магнитном поле проводником за малое время dt, можно определить как площадь треугольника, равную половине произведения основания L на высоту da.
Высота треугольника при малом dt совпадает с длиной дуги, опирающейся на угол .
Слайд 26Тогда площадь dS выразится как
.
Учтём, что угловая скорость вращения .
Для ЭДС индукции соответственно получится формула:
Слайд 274.4. Переменная ЭДС индукции. Переменный ток
Рассмотрим вращение замкнутого проводящего контура
в магнитном поле постоянного магнита.
S - площадь, ограниченная контуром;
В –
магнитная индукция;
N – количество витков;
- угловая скорость вращения контура.
Контур вращается вокруг оси, перпендикулярной силовым линиям магнитного поля и проходящей через диаметр контура.
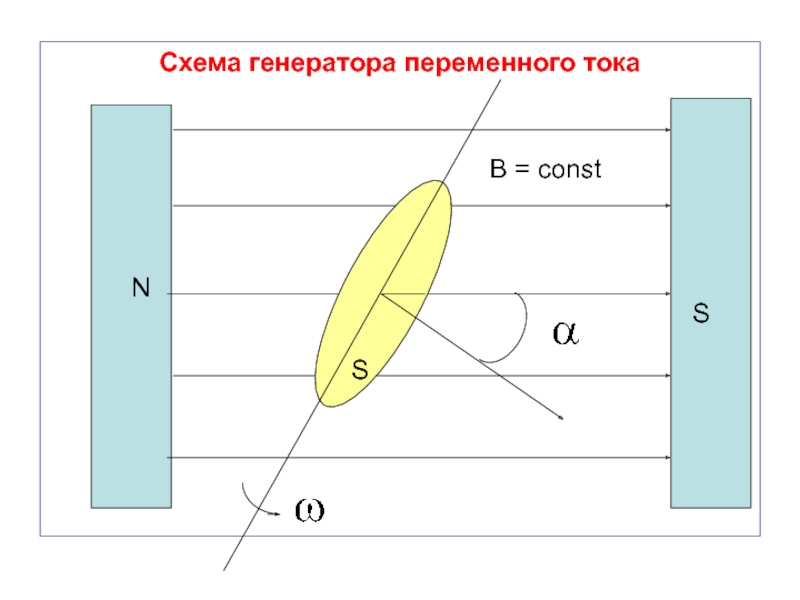
Слайд 28Схема генератора переменного тока
N
S
B = const
S
Слайд 29При вращении меняется угол между нормалью к плоскости контура и
линиями индукции магнитного поля.
Магнитный поток, пересекающий плоскость контура, изменяется со
временем по гармоническому закону:
ЭДС индукции определим по закону Фарадея:
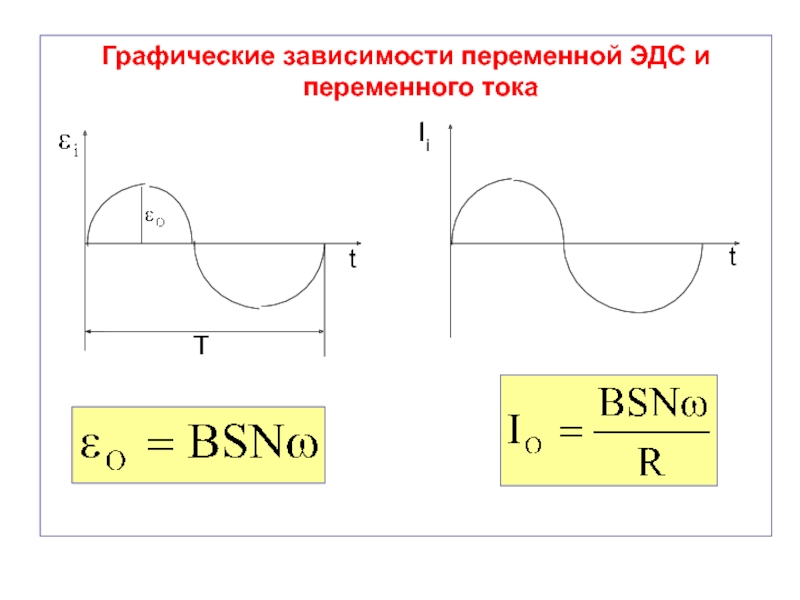
Слайд 30Последнее выражение называется переменной ЭДС индукции и записывается короче:
Максимальное значение
переменной ЭДС индукции называется амплитудным значением:
Частота колебаний переменной ЭДС индукции
и период её изменения Т связаны соотношением:
Слайд 31Разделив значение переменной ЭДС на сопротивление контура, получим переменный индукционный
ток:
Амплитудное значение переменного тока:
Переменный ток – это ток, изменяющийся по
величине и направлению по закону синуса (или косинуса).
Слайд 32Графические зависимости переменной ЭДС и переменного тока
t
T
Ii
t
Слайд 33Переменный ток применяется в промышленных электрических сетях.
Частота его колебаний
50 Гц.
Ранее на рисунке представлен генератор переменного тока, в котором
в магнитном поле вращается рамка, имеющая много витков.
Если якорь этого генератора сделан из нескольких секций, то вокруг него можно вращать магнитное поле.
Такое устройство называется генератором постоянного тока.
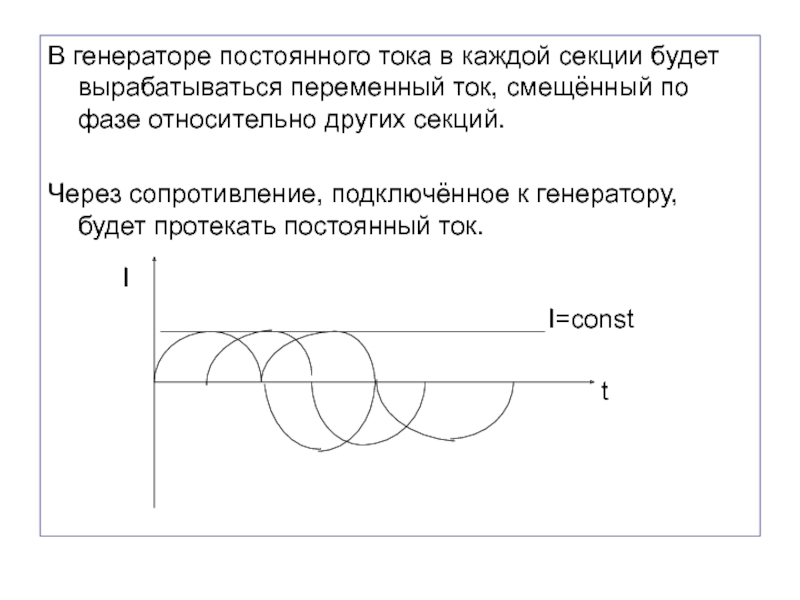
Слайд 34В генераторе постоянного тока в каждой секции будет вырабатываться переменный
ток, смещённый по фазе относительно других секций.
Через сопротивление, подключённое
к генератору, будет протекать постоянный ток.
I
t
I=const
Слайд 374.5.Самоиндукция.
Индуктивность соленоида
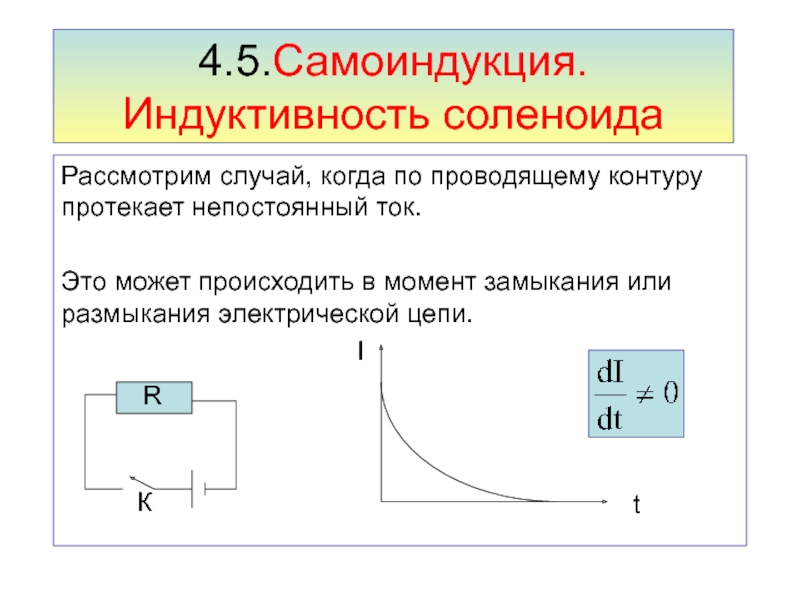
Рассмотрим случай, когда по проводящему контуру протекает непостоянный ток.
Это
может происходить в момент замыкания или размыкания электрической цепи.
К
R
I
t
Слайд 38Изменяющийся во времени ток проводимости образует в окружающем пространстве непостоянное
магнитное поле.
Обусловленный током проводимости магнитный поток Ф сквозь замкнутый контур
пропорционален величине тока:
В общем случае изменение магнитного потока можно записать как:
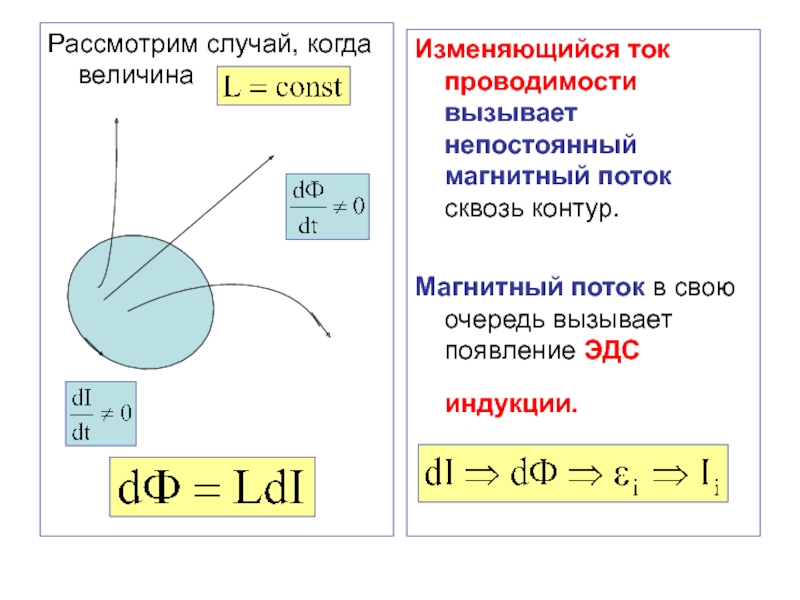
Слайд 39Рассмотрим случай, когда величина
Изменяющийся ток проводимости вызывает непостоянный магнитный
поток сквозь контур.
Магнитный поток в свою очередь вызывает появление ЭДС
индукции.
Слайд 40В контуре наряду с током проводимости будет протекать индукционный ток.
Самоиндукция
– явление возникновения индукционного тока в том самом замкнутом проводящем
контуре, по которому протекает непостоянный ток проводимости.
ЭДС самоиндукции прямо пропорциональна скорости изменения тока проводимости.
Слайд 41Коэффициент пропорциональности L называется индуктивностью контура.
Индуктивность:
равна ЭДС самоиндукции, возникающей в
замкнутом контуре при скорости изменения силы тока, равной единице;
равна магнитному
потоку сквозь площадь, ограниченную контуром, возникающему при единичном токе в этом контуре.
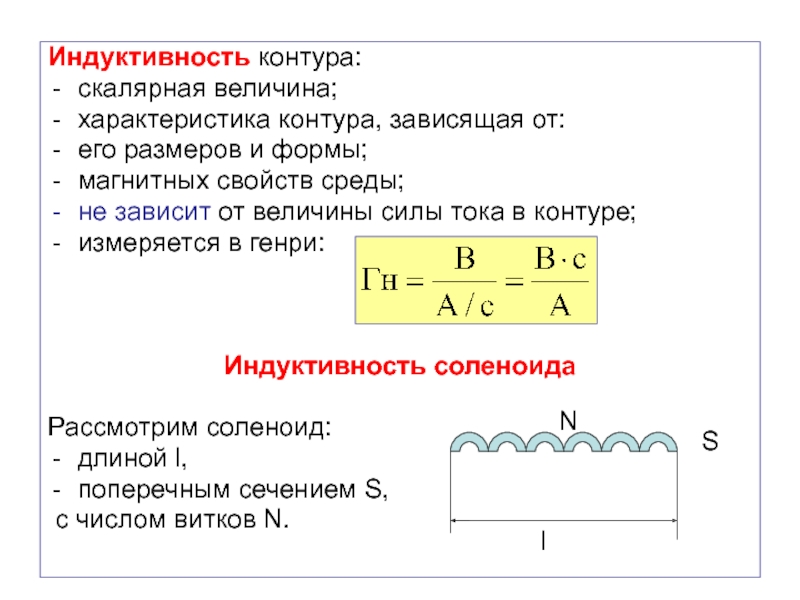
Слайд 42Индуктивность контура:
скалярная величина;
характеристика контура, зависящая от:
его размеров и формы;
магнитных свойств
среды;
не зависит от величины силы тока в контуре;
измеряется в генри:
.
Индуктивность соленоида
Рассмотрим соленоид:
длиной l,
поперечным сечением S,
с числом витков N.
l
N
S
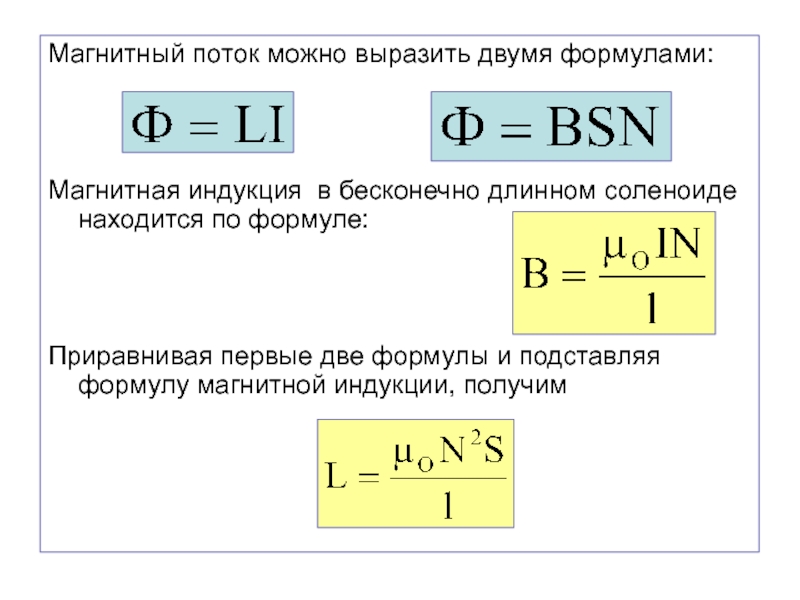
Слайд 43Магнитный поток можно выразить двумя формулами:
Магнитная индукция в бесконечно длинном
соленоиде находится по формуле:
Приравнивая первые две формулы и подставляя формулу
магнитной индукции, получим
Слайд 44Введём в рассмотрение густоту намотки n и объём соленоида V
:
При введении этих величин для индуктивности соленоида получим выражение:
Индуктивность соленоида
с сердечником увеличится в раз по сравнению с воздушным соленоидом:
Слайд 45Рассмотрим два проводящих сцеплённых между собой контура.
Между ними есть площадь
перекрытия S.
4.6. Взаимная индукция. Трансформатор
S
1
2
Слайд 46Если по первому контуру протекает непостоянный ток проводимости, (например, во
время замыкания цепи), то общий магнитный поток, пронизывающий оба контура,
вызывает во втором проводнике ЭДС взаимной индукции:
И наоборот:
Взаимная индукция – явление появления ЭДС индукции в одном замкнутом проводящем контуре при изменении тока проводимости в другом контуре, сцеплённым с первым.
Слайд 47ЭДС взаимной индукции, возникающей в одном контуре, прямо пропорциональна скорости
изменения силы тока в другом контуре.
Коэффициент пропорциональности М = М12
= М21 носит название коэффициент взаимной индукции (или взаимная индуктивность контуров).
Слайд 48Коэффициент взаимной индукции зависит от:
- размеров контуров;
площади перекрытия;
взаимного расположения контуров;
магнитных
свойств среды.
Не зависит от:
силы тока проводимости, вызвавшего появление ЭДС взаимной
индукции.
Коэффициент взаимной индукции:
- измеряется в генри: Гн = Вс/А.
для немагнитных сред пропорционален
Слайд 49На явлении взаимной индукции основано действие трансформатора, в котором на
общий сердечник из ферромагнитного материала намотаны первичная (I) и вторичная
(П) обмотки, имеющие различное число витков N1 и N2 соответственно..
Коэффициент взаимной индукции в этом случае определяется формулой
.
S – площадь сечения сердечника,
l – его длина.
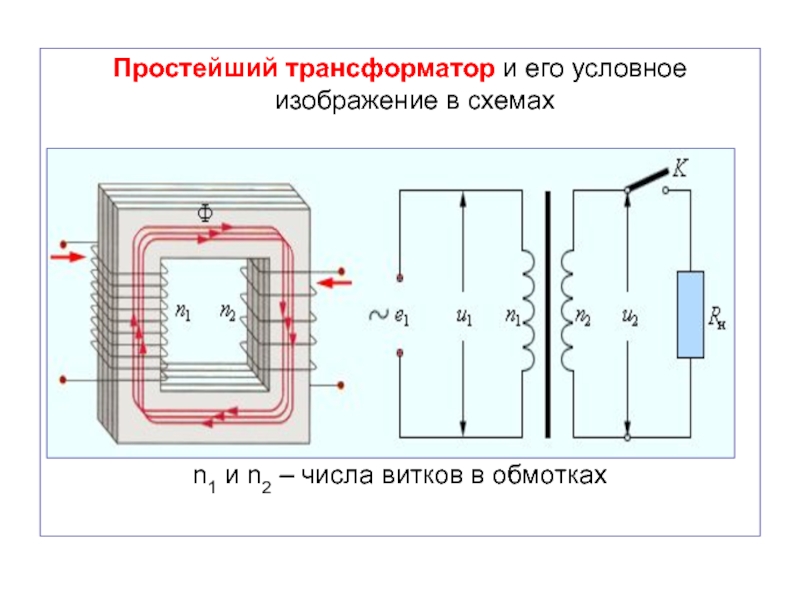
Слайд 50Простейший трансформатор и его условное изображение в схемах
n1 и
n2 – числа витков в обмотках
Слайд 51В цепи первичной обмотки трансформатора генерируется переменное напряжение определённой частоты
и амплитуды.
За счёт явления взаимной индукции во вторичной обмотке трансформатора
возникает переменная ЭДС индукции той же частоты, что и на первичной обмотке, но другой амплитуды.
Коэффициент трансформации: .
При трансформатор повышает амплитуду переменного напряжения.
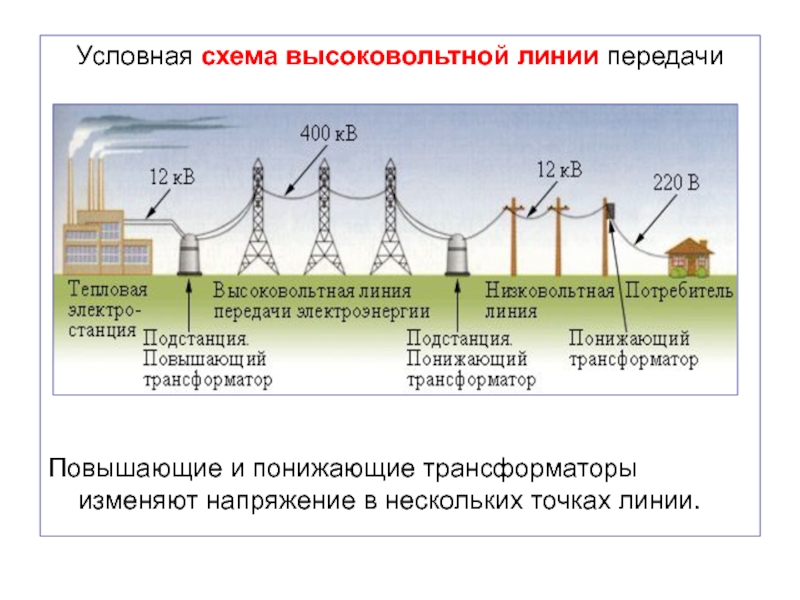
Слайд 52Условная схема высоковольтной линии передачи
Повышающие и понижающие трансформаторы изменяют
напряжение в нескольких точках линии.
Слайд 534.7. Токи при замыкании и размыкании электрических цепей
При размыкании и
замыкании электрической цепи изменение тока происходит не мгновенно, а постепенно.
При
замыкании цепи ток в ней нарастает постепенно от нуля до максимального значения.
При размыкании цепи ток убывает от максимального значения до нуля.
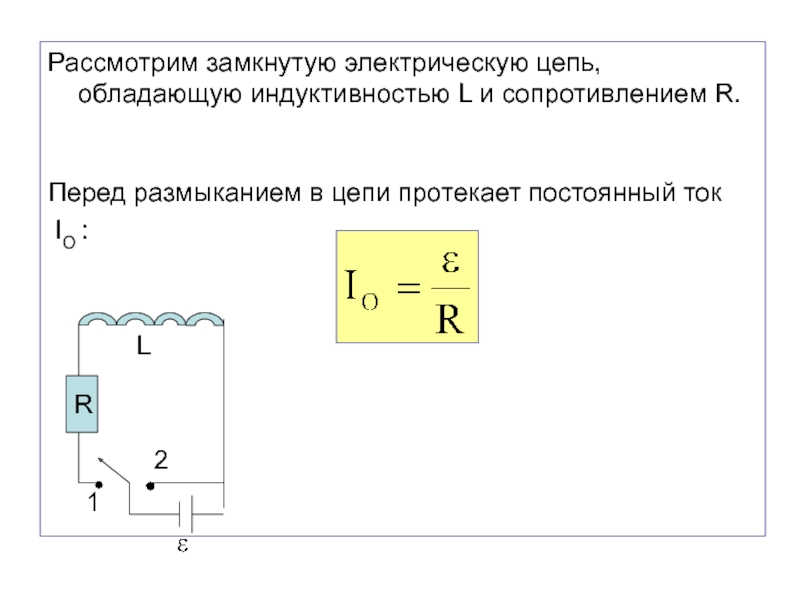
Слайд 54Рассмотрим замкнутую электрическую цепь, обладающую индуктивностью L и сопротивлением R.
Перед размыканием в цепи протекает постоянный ток
IO :
R
1
2
L
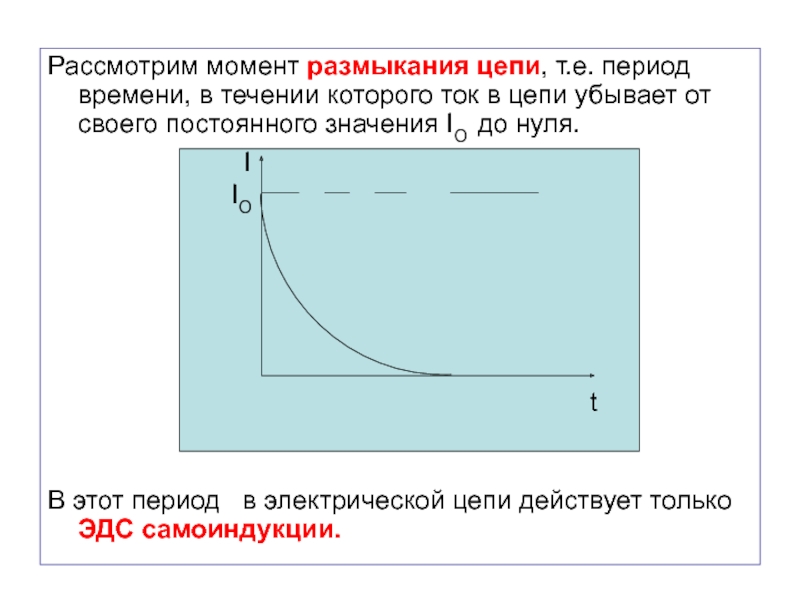
Слайд 55Рассмотрим момент размыкания цепи, т.е. период времени, в течении которого
ток в цепи убывает от своего постоянного значения IO до
нуля.
В этот период в электрической цепи действует только ЭДС самоиндукции.
I
IO
t
Слайд 56При отключении источника тока в начальный (нулевой) момент времени сразу
ток начнёт убывать.
Моментально возникнет ЭДС самоиндукции, противодействующая уменьшению силы тока.
При использовании второго правила
Кирхгофа, закона Ома и формулы
ЭДС самоиндукции получим
следующие преобразования:
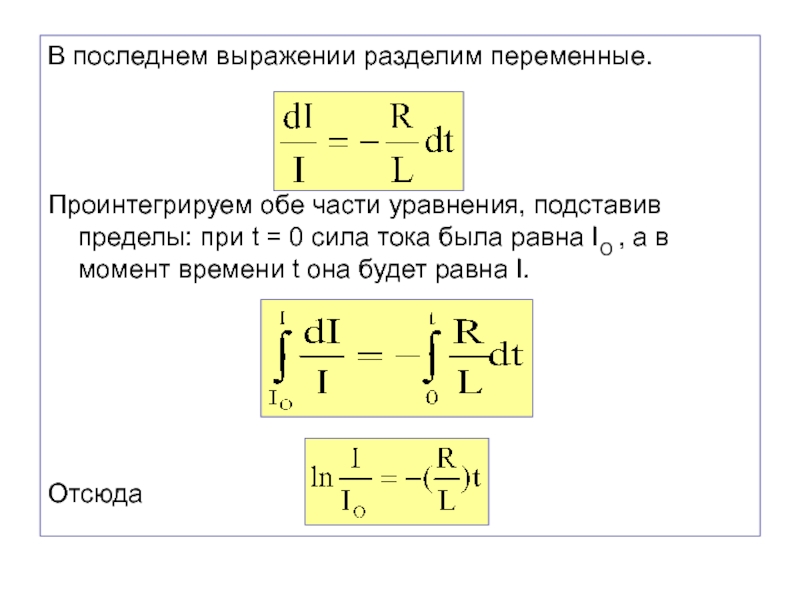
Слайд 57В последнем выражении разделим переменные.
Проинтегрируем обе части уравнения, подставив пределы:
при t = 0 сила тока была равна IO ,
а в момент времени t она будет равна I.
Отсюда
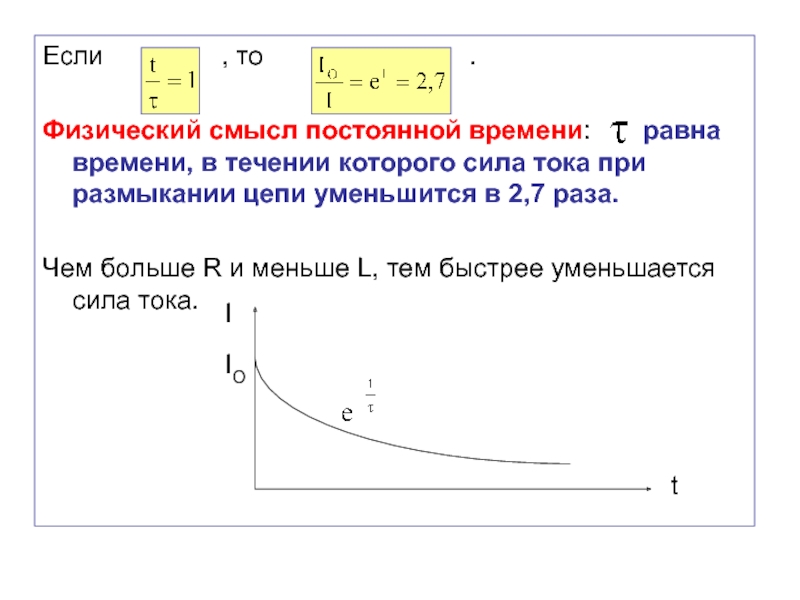
Слайд 58Потенцируя последнее выражение, окончательно получим закон изменения тока при размыкании
цепи:
сила тока при размыкании электрической цепи убывает по экспоненциальному закону.
Скорость
убывания силы тока определяет величина , называемая постоянной времени:
.
Физический смысл постоянной времени: равна времени, в течении которого сила тока при размыкании цепи уменьшится в 2,7 раза.
Чем больше R и меньше L, тем быстрее уменьшается сила тока.
I
t
IO
Слайд 60При замыкании электрической цепи в ней действуют две ЭДС (источника
тока и самоиндукции).
Сила тока нарастает по экспоненциальному закону согласно формуле:
t
I
Слайд 614.8. Вихревые токи (токи Фуко)
Жан Берна́р Лео́н Фуко́ (1819 -
1868) - французский физик и астроном.
Слайд 62Токи Фуко:
возникают под воздействием переменного электромагнитного поля;
по своей физической природе
ничем не отличаются от индукционных токов, возникающих в линейных проводах;
вихревые,
то есть замкнуты в кольца;
достигают очень большой величины, так как в массивных образцах выбирают путь наименьшего сопротивления.
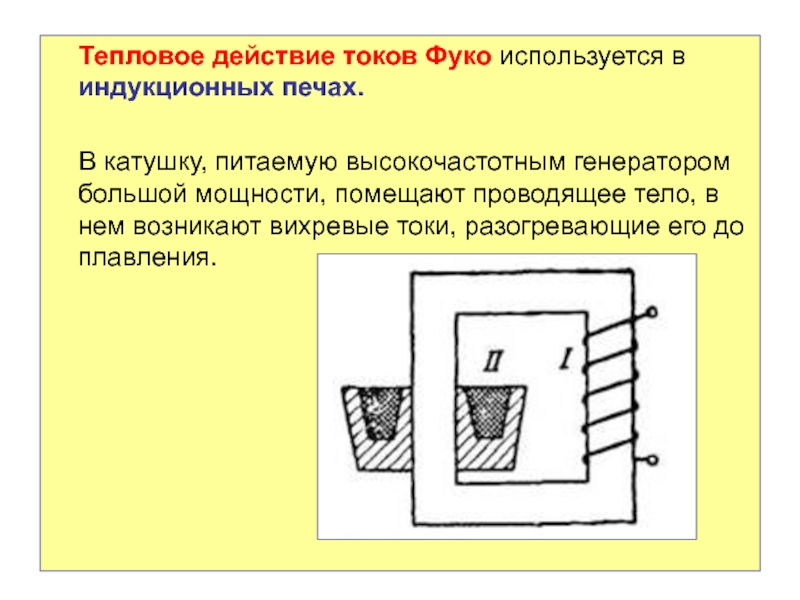
Слайд 63Тепловое действие токов Фуко используется в индукционных печах.
В катушку, питаемую
высокочастотным генератором большой мощности, помещают проводящее тело, в нем возникают
вихревые токи, разогревающие его до плавления.
Слайд 64Метод закалки металлов за счёт токов Фуко получил название скин-эффект
(skin – кожа, кожура).
В мощном переменном поле поверхностные слои
металла разогреваются очень быстро, а остальная масса металла остаётся холодной.
Затем производится быстрое охлаждение.
Закалённая деталь имеет твёрдую поверхность, но не становится хрупкой.
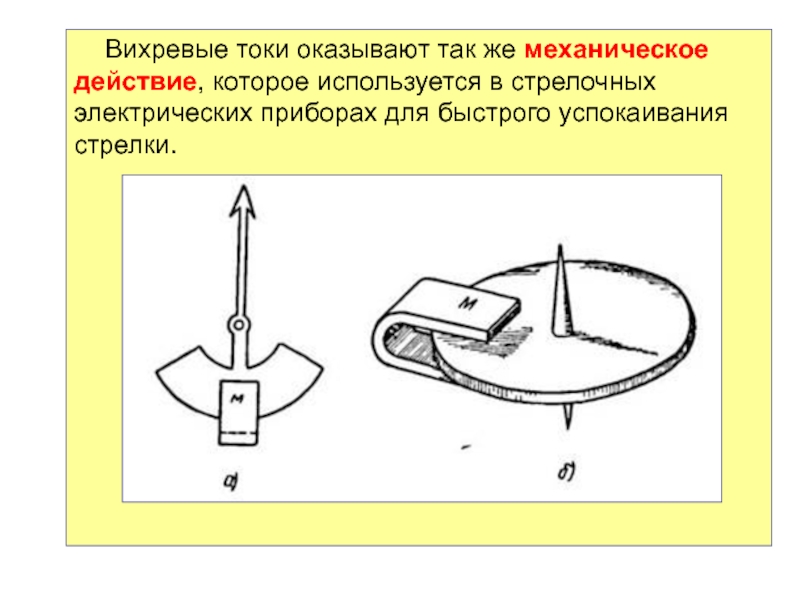
Слайд 65Вихревые токи оказывают так же механическое действие, которое используется в
стрелочных электрических приборах для быстрого успокаивания стрелки.
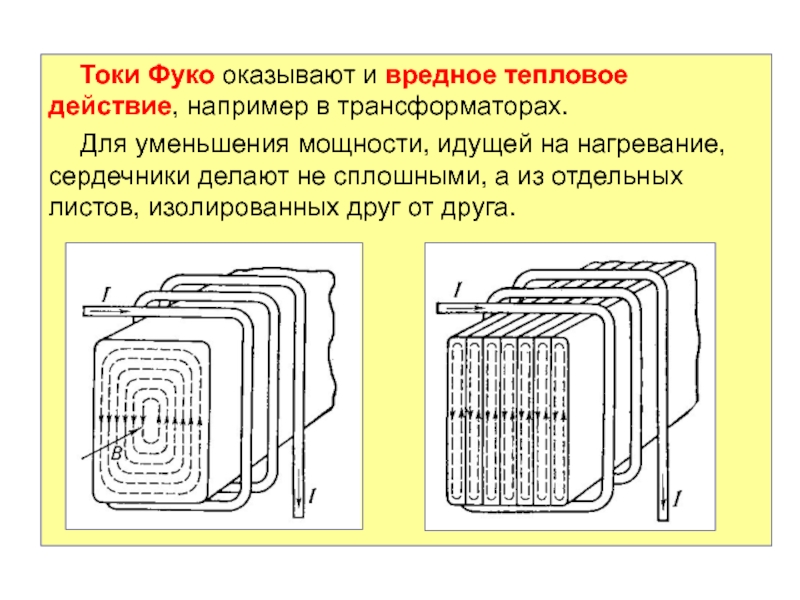
Слайд 66Токи Фуко оказывают и вредное тепловое действие, например в трансформаторах.
Для уменьшения мощности, идущей на нагревание, сердечники делают не сплошными,
а из отдельных листов, изолированных друг от друга.
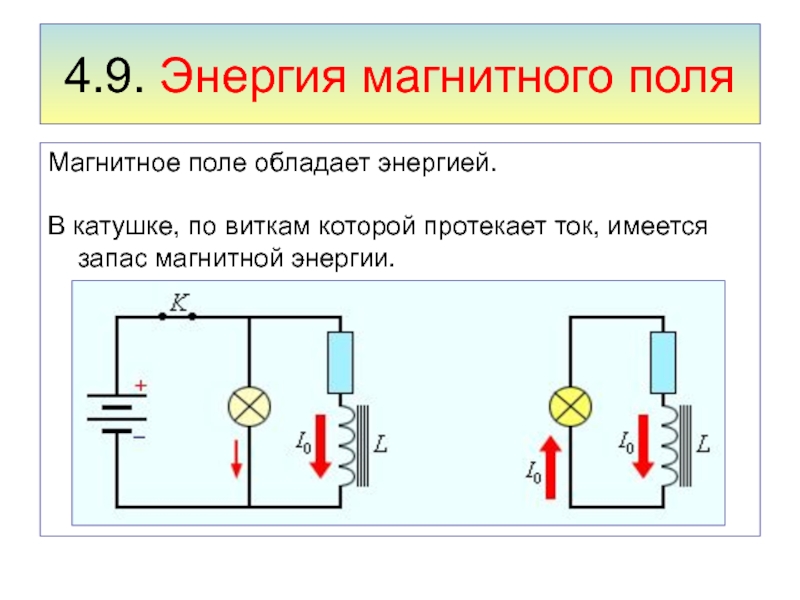
Слайд 67Магнитное поле обладает энергией.
В катушке, по виткам которой протекает
ток, имеется запас магнитной энергии.
4.9. Энергия магнитного поля
Слайд 68Если включить электрическую лампу параллельно катушке с большой индуктивностью в
электрическую цепь постоянного тока, то при размыкании ключа наблюдается кратковременная
вспышка лампы.
Ток в цепи возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
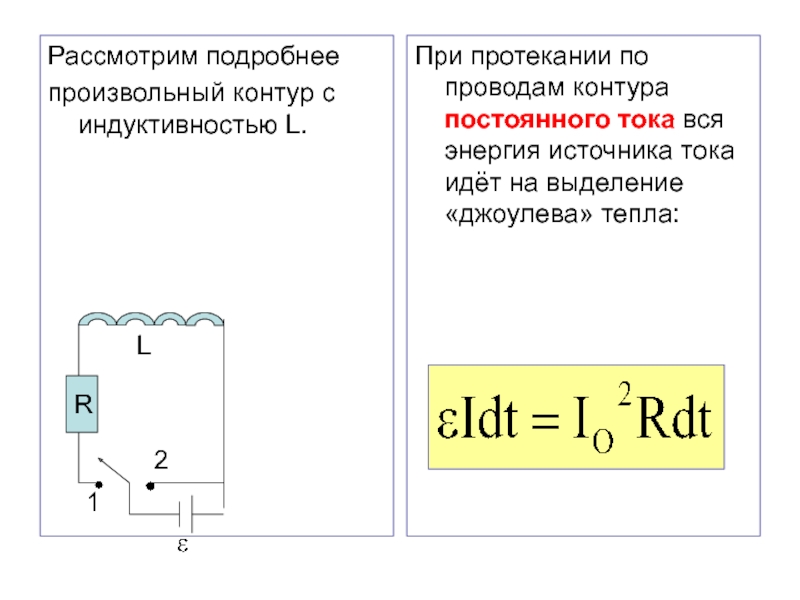
Слайд 69Рассмотрим подробнее
произвольный контур с индуктивностью L.
При протекании по проводам
контура постоянного тока вся энергия источника тока идёт на выделение
«джоулева» тепла:
R
1
2
L
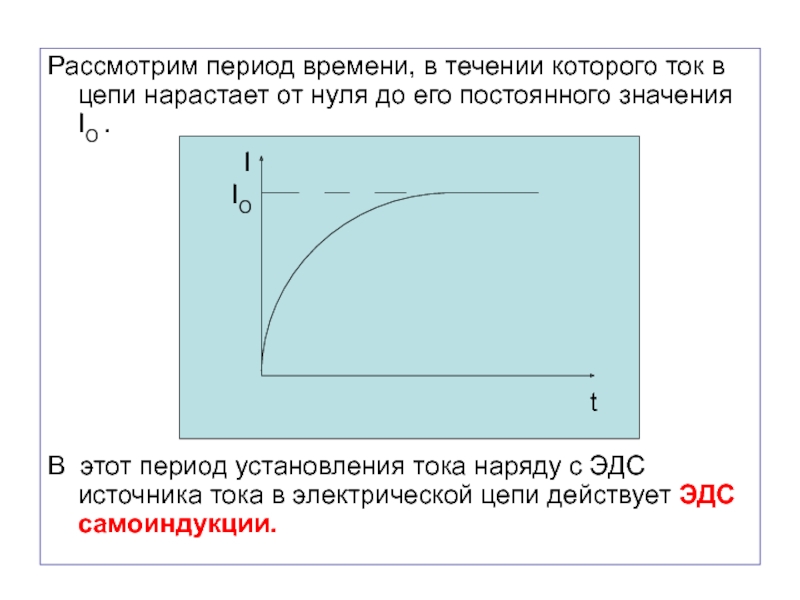
Слайд 70Рассмотрим период времени, в течении которого ток в цепи нарастает
от нуля до его постоянного значения IO .
В этот период
установления тока наряду с ЭДС источника тока в электрической цепи действует ЭДС самоиндукции.
I
IO
t
Слайд 71В момент замыкания цепи, когда сила тока I меньше
IO , «джоулева» тепла выделяется меньше, но энергия источника остаётся
постоянной.
Для этого периода времени запишем закон Ома:
Выразим величину
Слайд 72Умножим обе части последнего равенства на величину Idt.
Это уравнение выражает
закон сохранения энергии в любой момент времени в период установления
тока.
Второе слагаемое представляет собой мгновенное значение энергии магнитного поля:
Полная энергия магнитного поля за весь период установления тока:
Слайд 73Таким образом, окончательно запишем формулу энергии магнитного поля в виде:
Преобразуем
эту формулу так, чтобы энергия поля определялась через характеристики поля:
магнитную индукцию В и напряжённость Н.
Для этого запишем формулу индуктивности соленоида
и энергию представим через объёмную плотность энергии w и объём соленоида V:
Слайд 74Тогда получим для объёмной плотности энергии выражение:
.
Учтём далее, что ток в соленоиде создаёт магнитную индукцию .
Окончательно
,
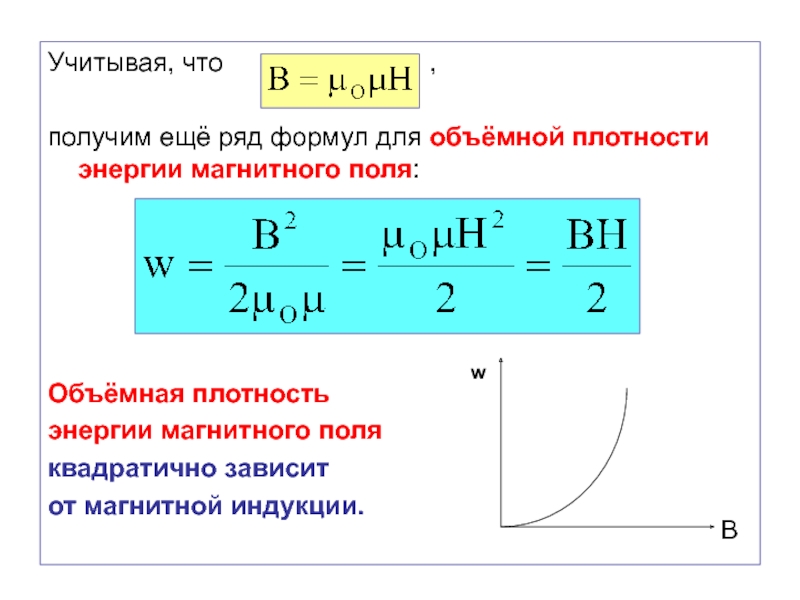
получим ещё ряд формул
для объёмной плотности энергии магнитного поля:
Объёмная плотность
энергии магнитного поля
квадратично зависит
от магнитной индукции.
w
B









![Мультимедийные лекции по физике ЭДС индукции измеряется в вольтах: [εi] = 1В.ЭДС индукции может возникать ЭДС индукции измеряется в вольтах: [εi] = 1В.ЭДС индукции может возникать в двух случаях:в постоянном магнитном поле](/img/thumbs/dc5b73037e48f63785d2f35ffee484e9-800x.jpg)