Слайд 1НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Автор презентации:
доцент кафедры «Инженерная графика»
Тамара Владимировна Нестерова
Слайд 2ВВЕДЕНИЕ
Начертательная геометрия (НГ) – это дисциплина, которая
поможет Вам увидеть
окружающий мир другими глазами – глазами инженера
подготовит к изучению машиностроительного
черчения, созданию чертежа
позволит сделать первый шаг в мир творчества, созидания, изобретений и открытий
Слайд 6ОСНОВОПОЛОЖНИКИ НГ
Создатель этих вечных живописных полотен – Леонардо да Винчи
Секрет
Мастера раскрывается в его умении смотреть на окружающие предметы глазами
Великого Геометра
Слайд 7ОСНОВОПОЛОЖНИКИ НГ
Леонардо да Винчи
Слайд 8ИСТОРИЧЕСКАЯ СПРАВКА
Леонардо да Винчи, родился 15 апреля 1452 по юлианскому
календарю в городке Винчи - один из наиболее известных художников
мира; также один из самых талантливых людей в истории - учёный-исследователь, инженер, изобретатель, музыкант, архитектор, литератор, театральный художник-постановщик и режиссер, дизайнер одежды - добившийся во всех областях своей деятельности блестящих результатов, часто намного опережая своё время
Слайд 9ИЗОБРЕТЕНИЯ ДА ВИНЧИ
Летательный аппарат
Слайд 10ИЗОБРЕТЕНИЯ ДА ВИНЧИ
Осадный арбалет
Слайд 11ОСНОВОПОЛОЖНИКИ НГ
Гаспа́р Монж, граф де Пелю́з. Родился во Франции в
1746 году в местечке Бон, — французский математик, геометр, государственный
деятель, морской министр
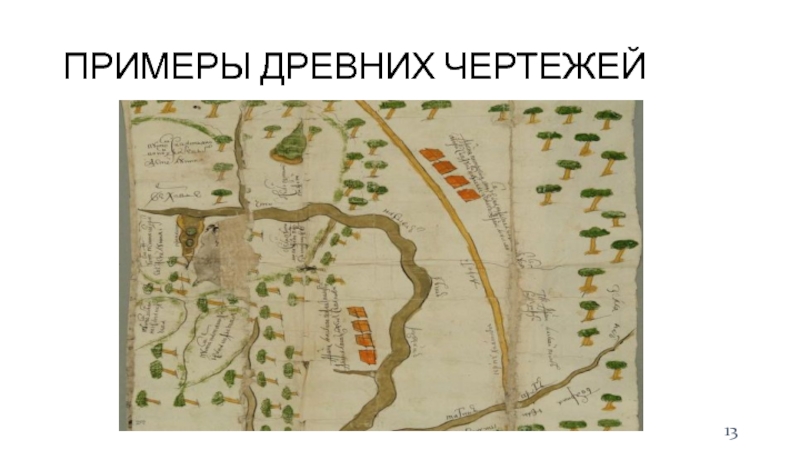
Слайд 12ИСТОКИ РАЗВИТИЯ ЧЕРТЕЖА
Современные методы технической (и в том числе компьютерной)
графики имеют свою многовековую историю. Общение людей друг с другом
научило человека не только словесной речи, но и письменности.
Прежде чем появились буквы, из которых можно было составить написанное слово, человек выражал свою мысль рисунком
Древнейшие памятники истории сохранили изображения зверей, оружия, домашней утвари. История письменности приводит много примеров «картинного письма», в котором образы, предметы изображались рисунком. Позднее человеку понадобилось умение нарисовать не только такой предмет, который он видел, но и такой, который он хотел сделать
Когда стали возводиться большие сооружения — жилища, храмы, крепости, — возникли первые чертежи — планы. Они вычерчивались на земле в том месте, где должно было воздвигаться сооружение
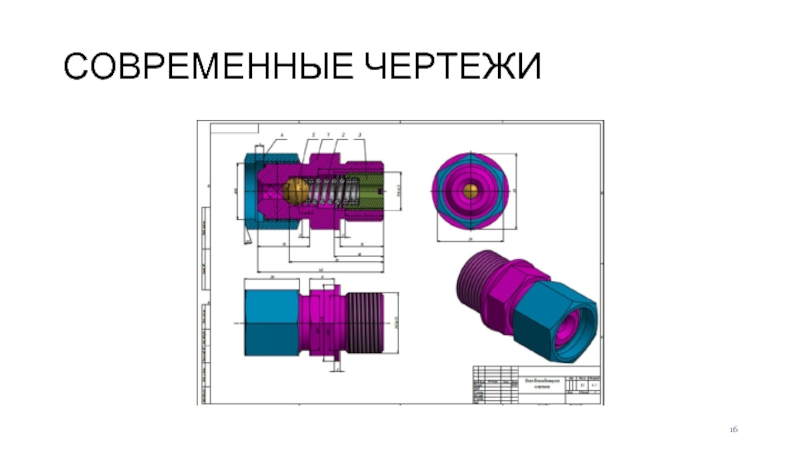
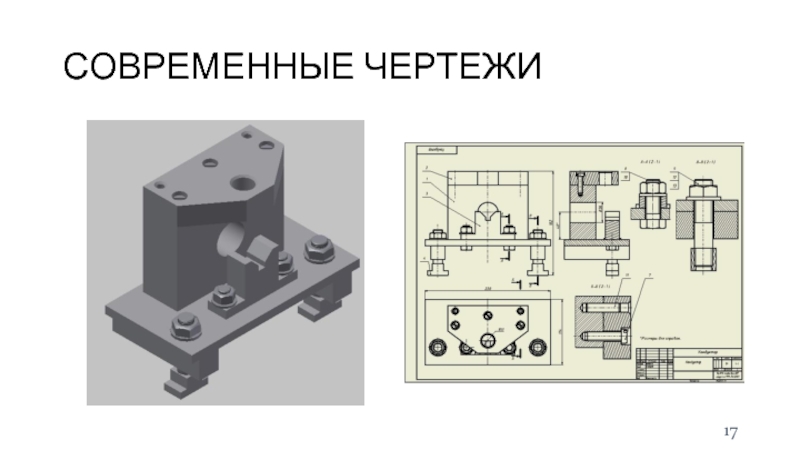
Слайд 15СОВРЕМЕННЫЕ ЧЕРТЕЖИ
Построение в 3D
Слайд 18ГРАФИК ИЗУЧЕНИЯ НГ
8 лекций в течение первого полусеместра (8 недель).
Цель лекции – получение навыка графического решения задачи по рассматриваемой
теме
16 практических занятий (1 семестр). Цель практических занятий – контроль знаний по темам дисциплины и помощь в освоении алгоритмов решения графических задач
Слайд 19ИНСТРУМЕНТЫ И МАТЕРИАЛЫ
На лекциях и практических занятиях для решения графических
задач нужны чертежные инструменты:
Треугольники (углы 45°, 30°)
Циркуль
Ластик
1 тетрадь
в клетку для лекционных и практических занятий
5 стандартных форматов А3 для выполнения РГР
Слайд 21ЦЕЛЬ КУРСА НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ
Развитие пространственного представления и воображения, необходимых в
техническом творчестве
Для создания представления о пространственном объекте по его
проекциям необходима некоторая работа воображения, тем большая, чем сложнее форма предмета
Научиться не только строить изображения предметов, но и мысленно воспроизводить в пространстве сами предметы по их изображениям
Слайд 22ЛИТЕРАТУРА
Конакова И.П., Нестерова Т.В. Базовый курс начертательной геометрии: учеб. Пособие
для студентов вузов. Екатеринбург: Уральский федеральный университет (УрФУ), 2019. http://elar.urfu.ru/bitstream/10995/66714/1/978-5-7996-2535-1_2019.pdf
Начертательная
геометрия и инженерная графика (открытое образование) / Н.Х. Понетаева, Т.В. Нестерова, Т.И. Кириллова, А.В., Щербаков А.В. https://openedu.ru/course/urfu/GEOM/
Гордон, В. О. Курс начертательной геометрии: учеб. пособие для студентов вузов / В. О. Гордон, М. А. Семенцов-Огиевский ; под ред. В. О. Гордона. Изд. 27-е, стер. М.: Высшая школа, 2000.
Фролов, С. А. Начертательная геометрия: учеб. для студентов вузов, обучающихся по направлению подгот. дипломир. специалистов в обл. техники и технологии / С. А. Фролов. - 3-е изд., перераб. и доп. Москва: ИНФРА-М, 2011.
Слайд 23СТАНДАРТЫ
1. ГОСТ 2.104-2006 Единая система конструкторской документации. Основные надписи. http://docs.cntd.ru/document/1200001992
2. ГОСТ 2.301-68
Единая система конструкторской документации. Форматы.
https://standartgost.ru/g/%D0%93%D0%9E%D0%A1%D0%A2_2.301-68
3. ГОСТ 2.302-68 Единая система конструкторской документации.
Масштабы.
https://standartgost.ru/g/%D0%93%D0%9E%D0%A1%D0%A2_2.302-68
4. ГОСТ 2.303-68 Единая система конструкторской документации. Линии.
https://standartgost.ru/g/%D0%93%D0%9E%D0%A1%D0%A2_2.303-68
5. ГОСТ 2.304-81 Единая система конструкторской документации. Шрифты чертежные.
https://standartgost.ru/g/%D0%93%D0%9E%D0%A1%D0%A2_2.304-81
Слайд 24ЗАДАЧИ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ
Метрические – задачи на определение длин линий, размеров
углов, площадей, объемов
Позиционные – задачи на установление взаимного положения
и принадлежности рассматриваемых геометрических объектов
Слайд 25ГЕОМЕТРИЧЕСКИЕ ОБЪЕКТЫ
Точка
Прямая
Плоскость
Поверхность
Слайд 26ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
Точки в пространстве – прописными буквами латинского алфавита А,
В, С, …, а также цифрами
Линии в пространстве – по
точкам, определяющим линию, и строчными буквами латинского алфавита а, b, c …
Углы – строчными буквами греческого алфавита – φ (фи), ψ (пси), ω (омега), σ (сигма)
Плоскости – α (альфа), β (бета), γ (гамма), δ (дельта)
Слайд 27ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
Плоскости проекций – строчной буквой греческого алфавита П
Горизонтальная плоскость
П1
Фронтальная плоскость П2
Профильная плоскость П3
Любая дополнительная плоскость П4, П5, …
Пn
Слайд 28ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
Оси проекций – строчными буквами x, y, z
При введении
дополнительных плоскостей -
П₁/ П₄, П₂/ П₄, П₄/ П₅,
…
Проекции точек:
На плоскость α – Аα
На горизонтальную плоскость П₁ – А₁
На фронтальную плоскость П₂ – А₂
На профильную плоскость П₃ – А₃
На дополнительную плоскость П₄ – А₄
Слайд 29ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
Проекции линий –
по проекциям точек, определяющих
линию: A1B1’ A2B2’ A3B3
строчными буквами:
На горизонтальную плоскость
П₁ – m₁, n₁…
На фронтальную плоскость П₂ – m₂, n₂, …
На профильную плоскость П₃ – m₃, n₃, …
Слайд 30СИМВОЛЫ, ОБОЗНАЧАЮШИЕ ОТНОШЕНИЯ МЕЖДУ ГЕОМЕТРИЧЕСКИМИ ФИГУРАМИ
= Равенство
Параллельны
Подобны
Перпендикулярны
Конгруэнтны
Отображается
Пересекаются
∊ Принадлежит
Скрещиваются
Слайд 31ВОПРОС 1
Дано: отрезок АВ.
Обозначение горизонтальной проекции АВ - ...
Слайд 32МЕТОДЫ ПРОЕЦИРОВАНИЯ
Проецирование – замена реально существующего объекта его изображением на
плоскости, выполненным по определенным правилам с помощью проецирующего луча
Методы проецирования:
Центральное
Параллельное
Ортогональное
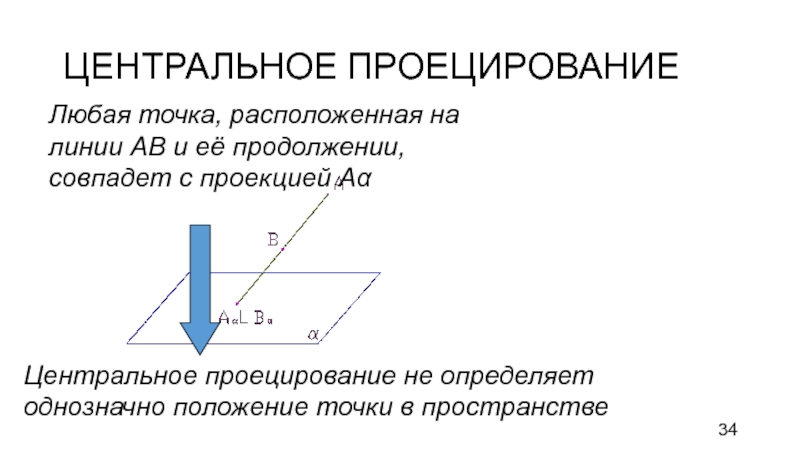
Слайд 33ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ
Проецирование предмета из данного центра называют центральным или коническим
проецированием. Чтобы спроецировать точку В на плоскость α из данного
центра А, надо провести прямую линию (проецирующий луч) из точки А через точку В до пересечения с плоскостью проекций α
Слайд 34ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ
Любая точка, расположенная на линии АВ и её продолжении,
совпадет с проекцией Аα
Центральное проецирование не определяет однозначно положение точки
в пространстве
Слайд 35ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ
Проецирование предмета из бесконечно удаленного центра называют параллельным или
цилиндрическим
Чтобы спроецировать точку А на плоскость α, надо провести
через эту точку параллельно направлению проецирования S прямую линию (проецирующий луч) до пересечения с плоскостью проекций α
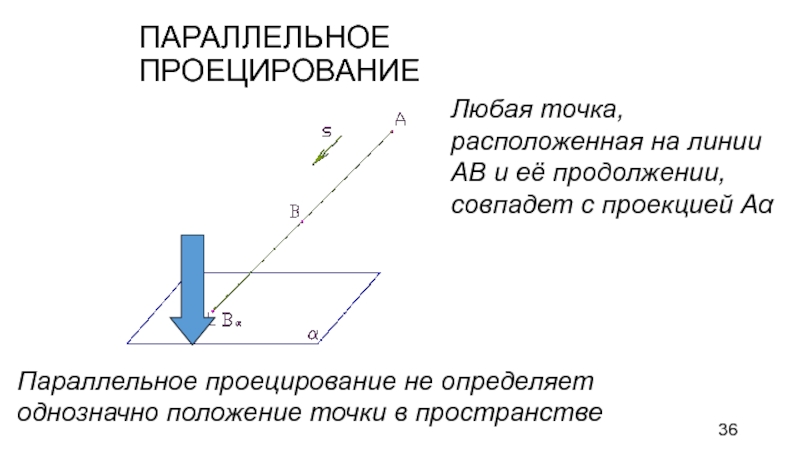
Слайд 36ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ
Любая точка, расположенная на линии АВ и её продолжении,
совпадет с проекцией Аα
Параллельное проецирование не определяет однозначно положение точки
в пространстве
Слайд 37ЦЕНТРАЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ. ВЫВОДЫ
Одна центральная проекция как и одна
параллельная проекция недостаточна для однозначного представления предмета:
по такому изображению
нельзя определить форму и размеры предмета и его положение в пространстве
Слайд 38ОРТОГОНАЛЬНОЕ (ПРЯМОУГОЛЬНОЕ) ПРОЕЦИРОВАНИЕ
Ортогональное проецирование – единственный способ построения машиностроительных
чертежей
Ортогональное проецирование – прямоугольное, параллельное проецирование на 3 взаимно перпендикулярные
плоскости
Прямоугольные проекции:
Наиболее распространены в конструкторской практике
Позволяют получить изображения, простые с точки зрения графических построений
Обеспечивают точное соотношение размеров изображений предметов на плоскости
Слайд 39ВОПРОС 2
Почему центральное проецирование не может использоваться для построения чертежа?
Слайд 40ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ
При ортогональном проецировании предметы располагают относительно плоскостей проекций
таким образом, чтобы их основные измерения были параллельны плоскостям проекций
При
этом предмет находится между наблюдателем и плоскостью проекций
Слайд 42ПОЛОЖЕНИЕ ТОЧКИ В ПРОСТРАНСТВЕ
Определение положения точек в пространстве производится по
их прямоугольным проекциям на двух и более плоскостях проекций
Слово «прямоугольный»
часто заменяют словом «ортогональный», образованным из слов древнегреческого языка, обозначающих «прямой» и «угол»
Слайд 43ДЕКАРТОВА СИСТЕМА КООРДИНАТНЫХ ОСЕЙ
Все пространственные объекты ориентируют относительно пространственной декартовой
системы координатных осей – системы трех взаимно перпендикулярных координатных плоскостей
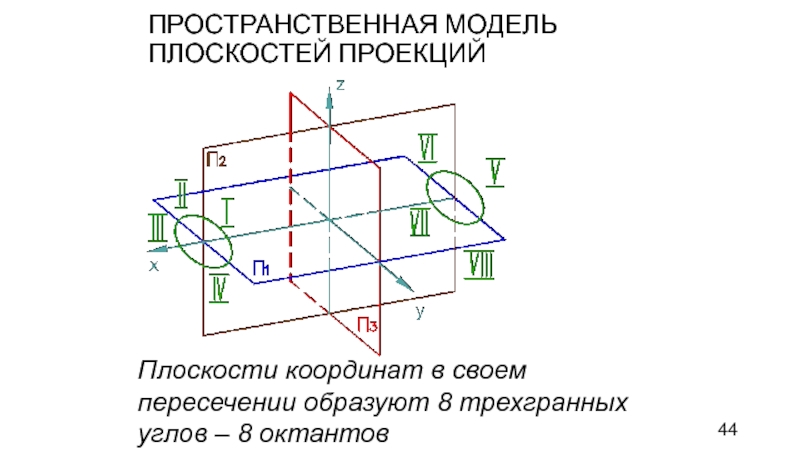
Слайд 44ПРОСТРАНСТВЕННАЯ МОДЕЛЬ ПЛОСКОСТЕЙ ПРОЕКЦИЙ
Плоскости координат в своем пересечении образуют 8
трехгранных углов – 8 октантов
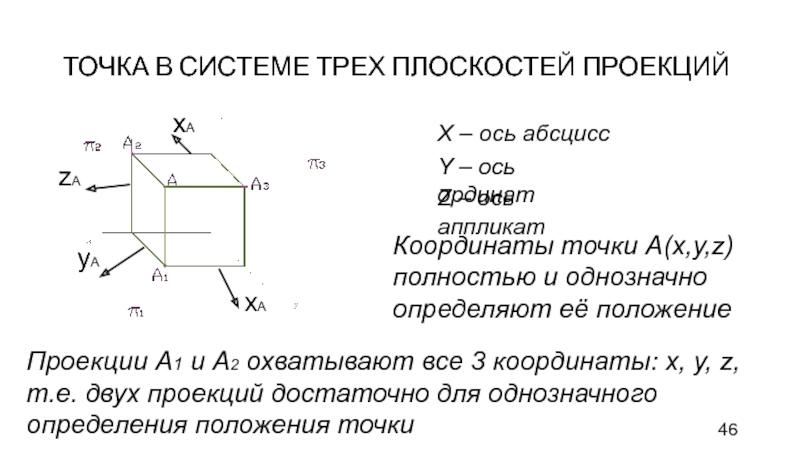
Слайд 46ТОЧКА В СИСТЕМЕ ТРЕХ ПЛОСКОСТЕЙ ПРОЕКЦИЙ
X – ось абсцисс
Y
– ось ординат
Z – ось аппликат
Координаты точки А(x,y,z) полностью и
однозначно определяют её положение
xA
yA
xA
zA
Проекции А1 и А2 охватывают все 3 координаты: x, y, z, т.е. двух проекций достаточно для однозначного определения положения точки
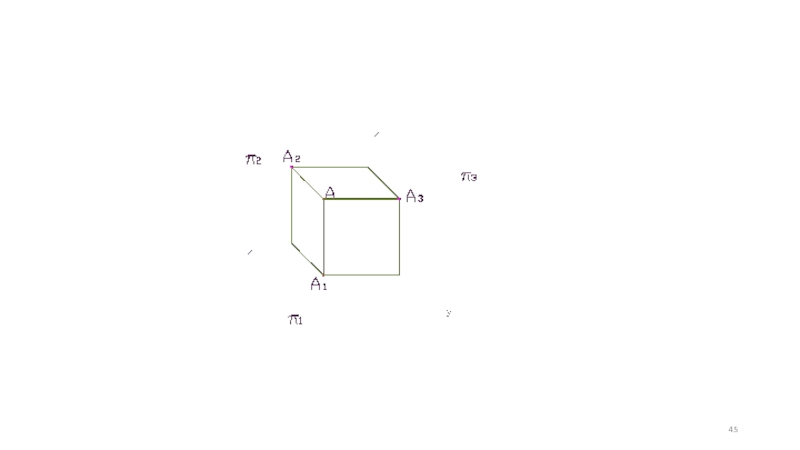
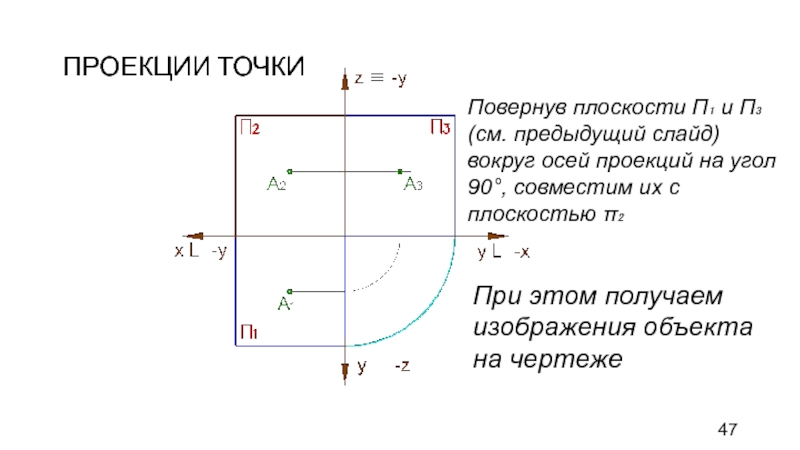
Слайд 47ПРОЕКЦИИ ТОЧКИ
Повернув плоскости П₁ и П₃ (см. предыдущий слайд) вокруг
осей проекций на угол 90°, совместим их с плоскостью π₂
При
этом получаем изображения объекта на чертеже
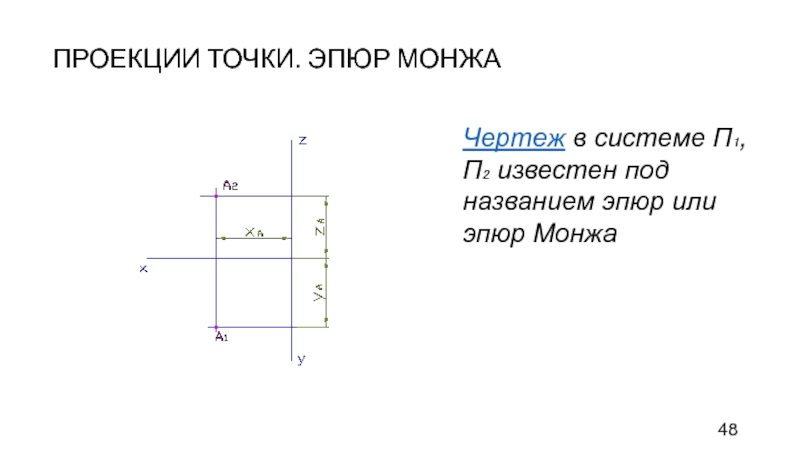
Слайд 48ПРОЕКЦИИ ТОЧКИ. ЭПЮР МОНЖА
Чертеж в системе П₁, П₂ известен под
названием эпюр или эпюр Монжа
Слайд 49ЧЕРТЕЖ
В дальнейшем эпюр Монжа, а также проекционные чертежи, в основе
которых лежит метод Монжа, будем называть одним словом - чертеж
- и понимать это слово только в указанном смысле. В других случаях применения слова «чертеж» оно будет сопровождаться соответствующим определением (перспективный чертеж, аксонометрический чертеж и т.п.) [3]
Слайд 50ВОПРОС 3
Вид проецирования, который используется при построении чертежа
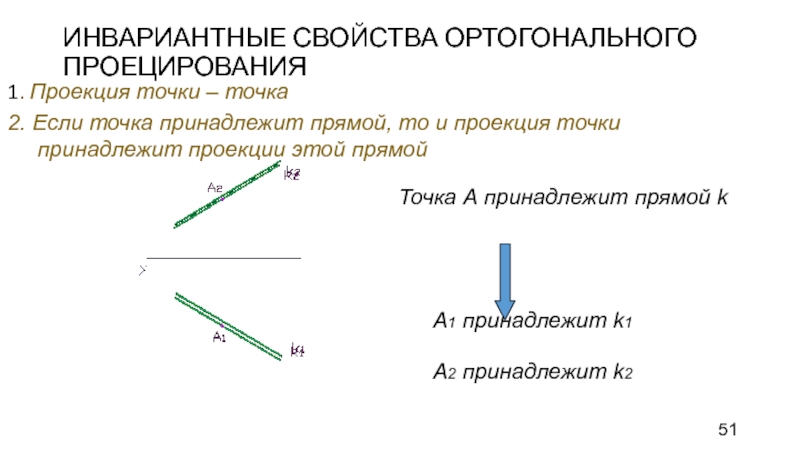
Слайд 51ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
1. Проекция точки – точка
2. Если точка
принадлежит прямой, то и проекция точки принадлежит проекции этой прямой
А1 принадлежит k1
А2 принадлежит k2
Точка А принадлежит прямой k
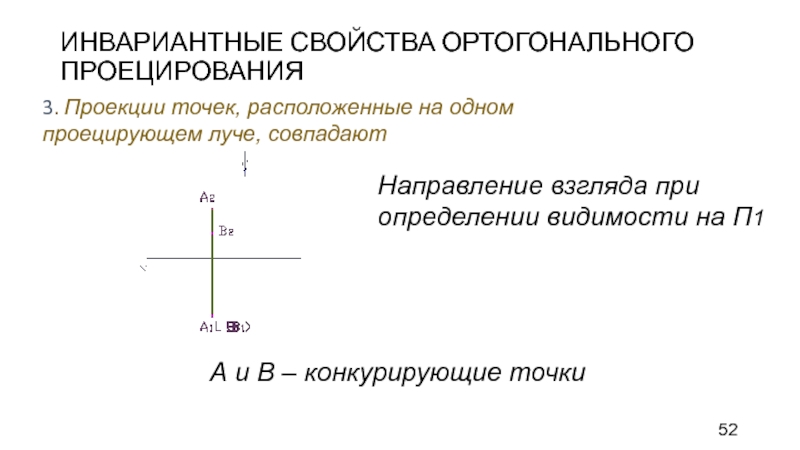
Слайд 52ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
3. Проекции точек, расположенные на одном проецирующем
луче, совпадают
Направление взгляда при определении видимости на П1
А и В
– конкурирующие точки
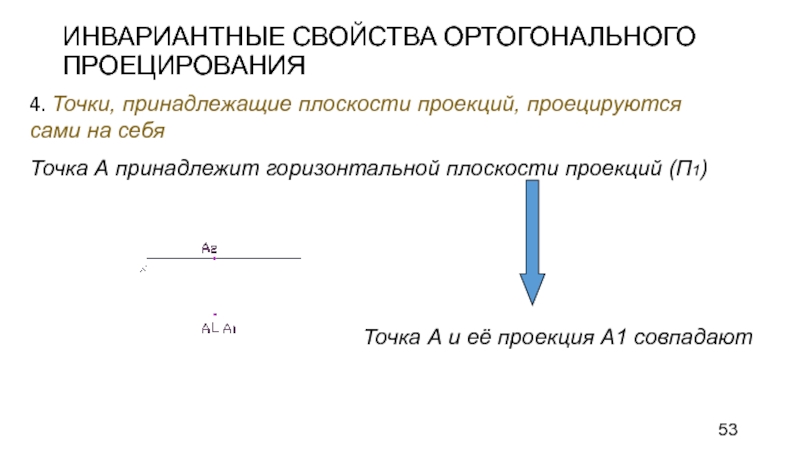
Слайд 53ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
4. Точки, принадлежащие плоскости проекций, проецируются сами
на себя
Точка А принадлежит горизонтальной плоскости проекций (П1)
Точка А и
её проекция А1 совпадают
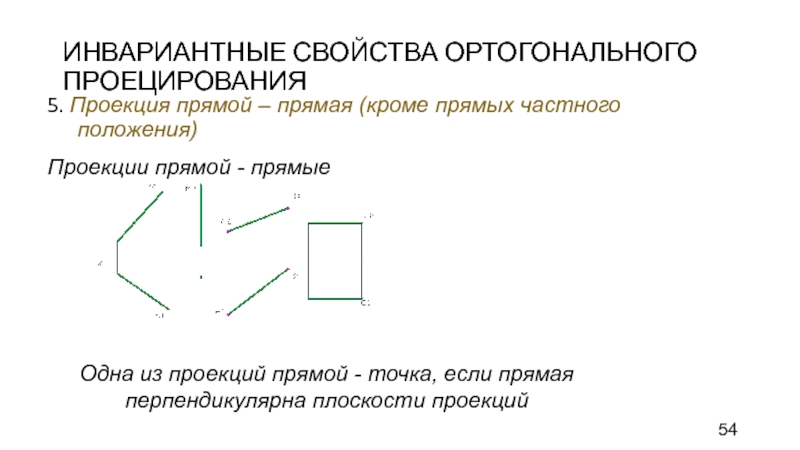
Слайд 54ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
5. Проекция прямой – прямая (кроме прямых
частного положения)
Проекции прямой - прямые
Одна из проекций прямой - точка,
если прямая перпендикулярна плоскости проекций
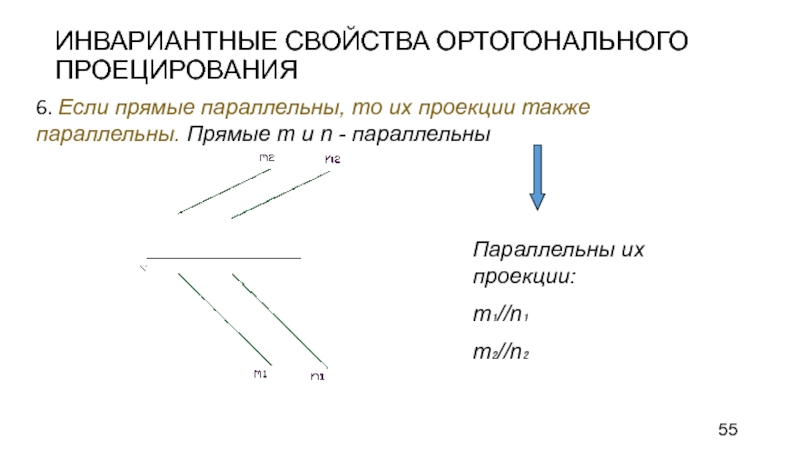
Слайд 55ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
6. Если прямые параллельны, то их проекции
также параллельны. Прямые m и n - параллельны
Параллельны их проекции:
m₁//n₁
m₂//n₂
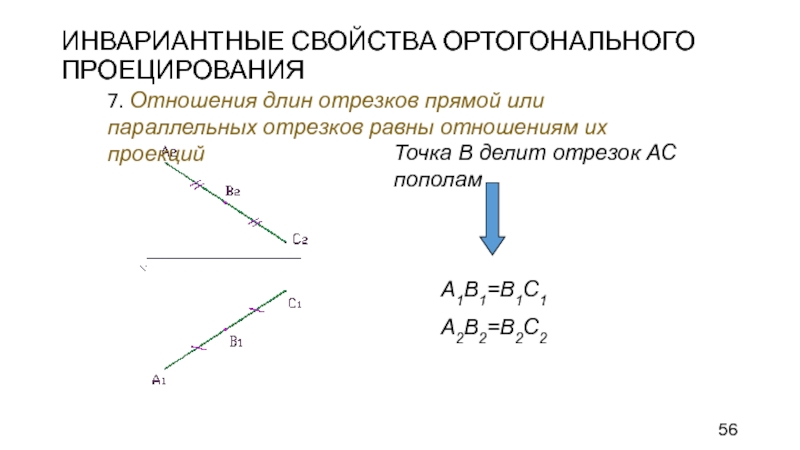
Слайд 56ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
7. Отношения длин отрезков прямой или параллельных
отрезков равны отношениям их проекций
А1В1=В1С1
А2В2=В2С2
Точка В делит отрезок АС пополам
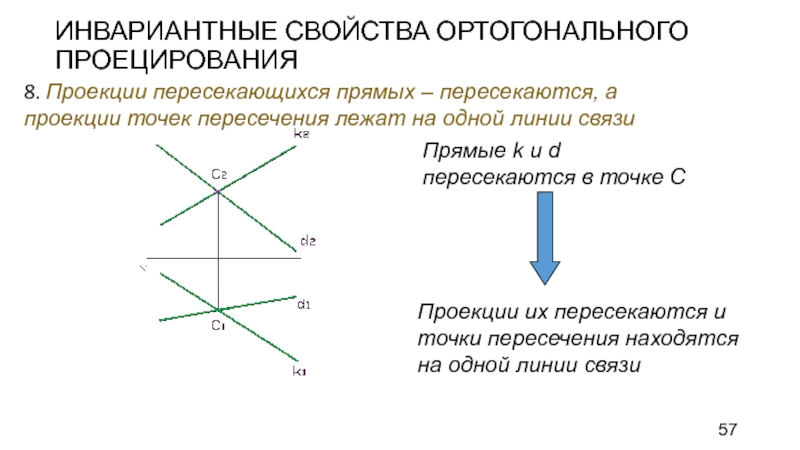
Слайд 57ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
8. Проекции пересекающихся прямых – пересекаются, а
проекции точек пересечения лежат на одной линии связи
Проекции их пересекаются
и точки пересечения находятся на одной линии связи
Прямые k и d пересекаются в точке С
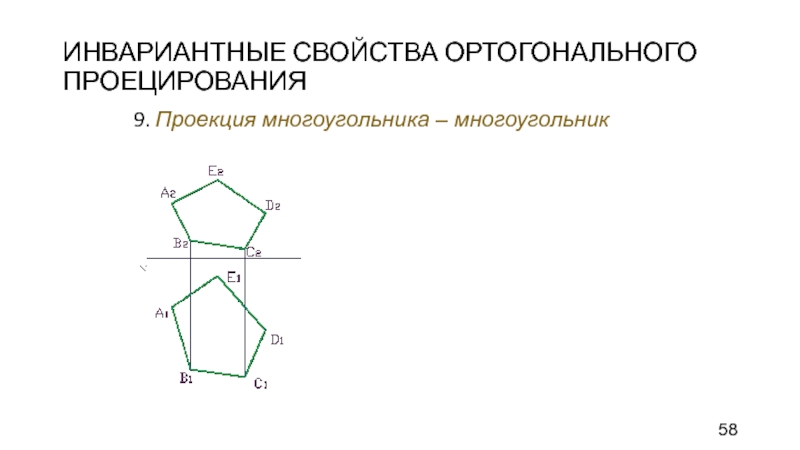
Слайд 58ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
9. Проекция многоугольника – многоугольник
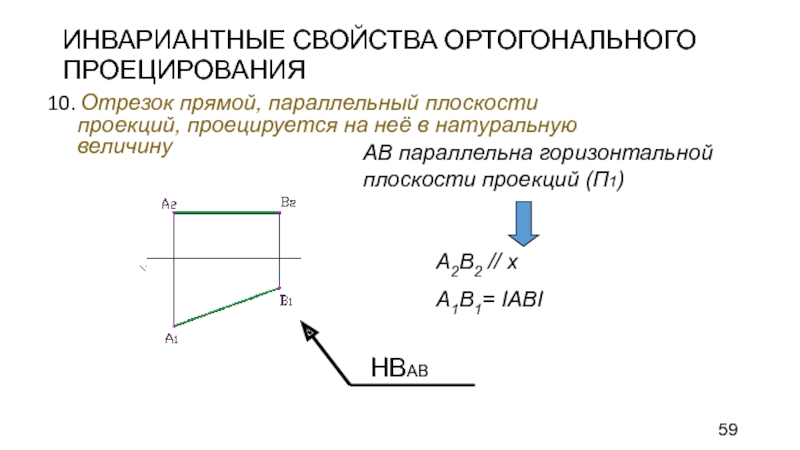
Слайд 59ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
10. Отрезок прямой, параллельный плоскости проекций, проецируется
на неё в натуральную величину
A2B2 // x
A1B1= IАВI
НВАВ
АВ параллельна горизонтальной
плоскости проекций (П1)
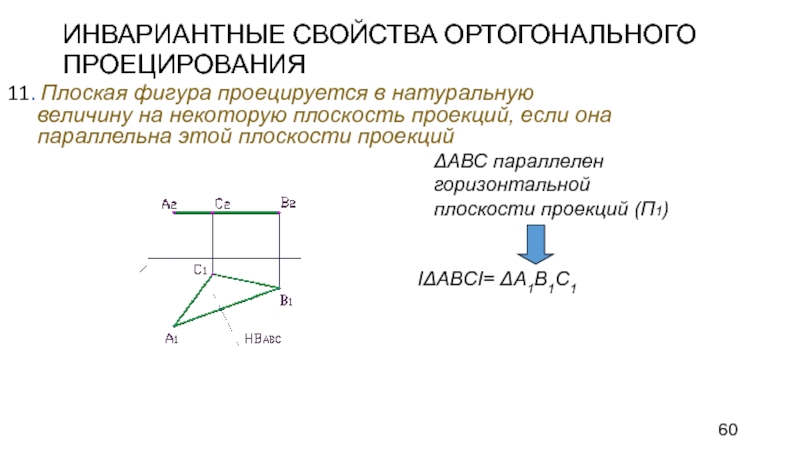
Слайд 60ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
11. Плоская фигура проецируется в натуральную величину
на некоторую плоскость проекций, если она параллельна этой плоскости проекций
IΔАВСI=
ΔА1В1С1
ΔАВС параллелен горизонтальной плоскости проекций (П1)
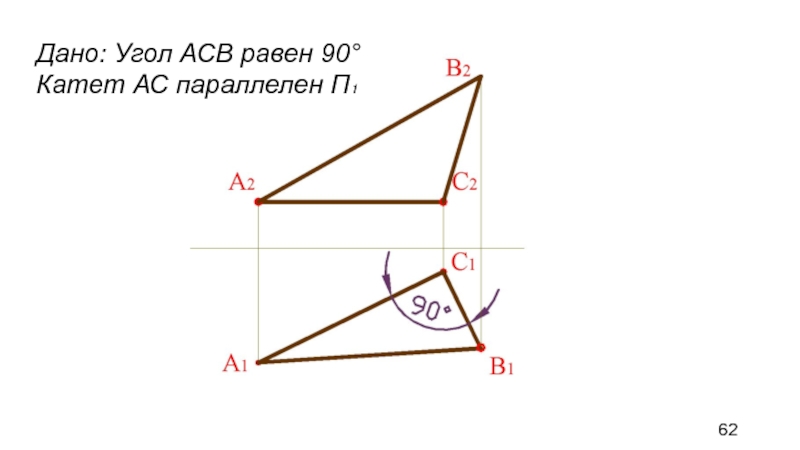
Слайд 61ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
12. Прямой угол, у которого хотя бы
один луч параллелен плоскости проекций, проецируется на неё в натуральную
величину
Слайд 62
Дано: Угол АСВ равен 90° Катет АС параллелен П₁
Слайд 63ВОПРОСЫ 4_5
4.Привести пример чертежа точки, принадлежащей П2
5.Условие, при котором прямой
угол проецируется на плоскость проекций в натуральную величину
Слайд 64ВЫВОДЫ
Ортогональное проецирование – прямоугольное, параллельное проецирование на три взаимно перпендикулярные
плоскости – единственный способ построения машиностроительных чертежей
Слайд 65ВЫВОДЫ
Положение точки определяется её ортогональными проекциями на две плоскости
По двум
проекциям всегда можно построить третью