Слайд 1Обучение без учителя
С/к «Распознавание образов»
Слайд 2Простой алгоритм выявления кластеров
Обучение без учителя
Слайд 3Простой алгоритм выявления кластеров
Пусть задано множество N образов {x1,x2,…,xN}.
Пусть центр
первого кластера z1 совпадает с любым из заданных образов и
определена произвольная неотрицательная пороговая величина T;
Будем считать, что z1 =x1.
Вычислим расстояние D21 между образом x2 и центром кластера z1 по формуле евклидова расстояния D = ||x-zi|| (1)
Если это расстояние больше пороговой величины T, то учреждается новый центр кластера z2=x2.
Слайд 4В противном случае образ x2 включается в кластер, центром которого
является z1.
Если условие D21 > T выполнено, то z2 является
центром нового кластера.
Далее вычисляются расстояния D31 и D32 до центров кластеров z1 и z2.
Если оба расстояния оказываются больше порогового значения T , то учреждается новый центр кластера z3=x3.
В противном случае x3 зачисляется в тот кластер, чей центр ему ближе.
Слайд 5Аналогично вычисляются расстояния от каждого нового образа xi до каждого
известного центра кластера zi и сравниваются с пороговой величиной T,
если все эти расстояния превосходят значения порога T, то учреждается центр кластера.
В противном случае образ зачисляется в кластер с самым близким к нему центром.
Результаты описанной процедуры определяются:
Выбором первого центра кластера;
Порядком обхода образов;
Значением пороговой величины T;
Геометрическими характеристиками данных.
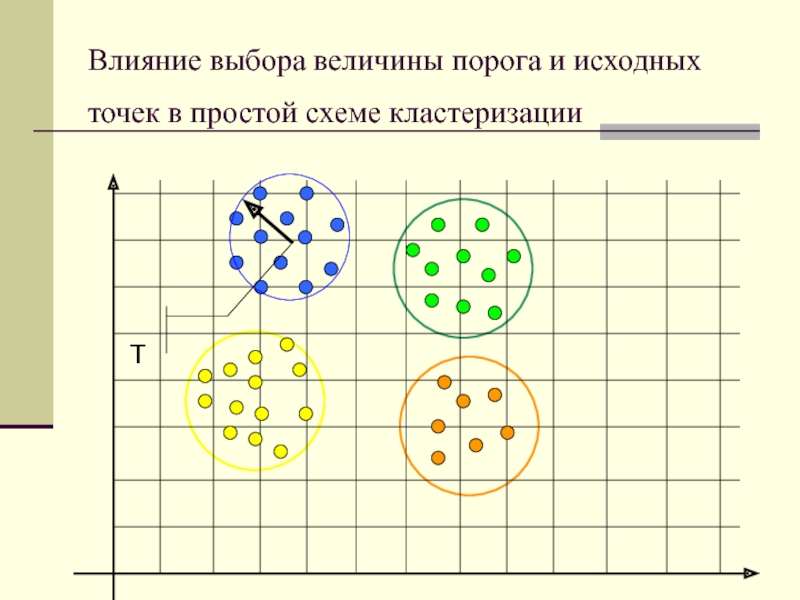
Слайд 6Т
Влияние выбора величины порога и исходных точек в простой схеме
кластеризации
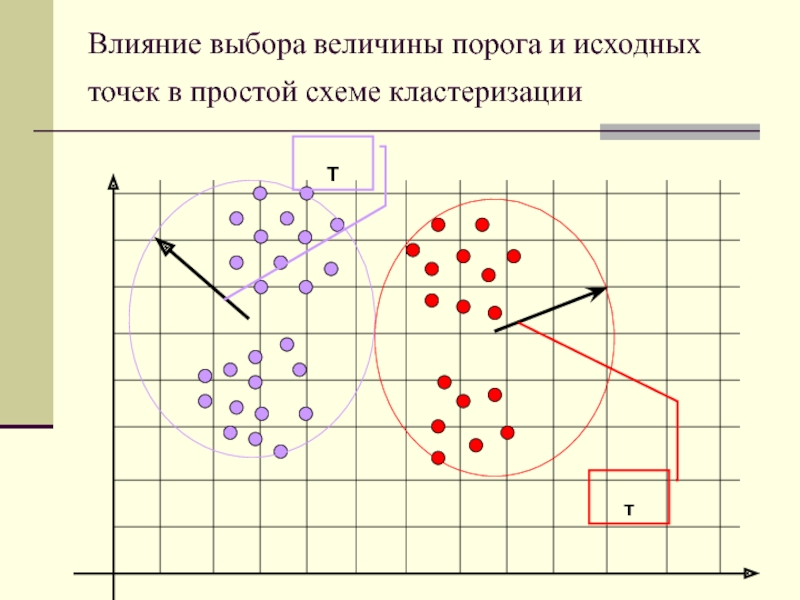
Слайд 7т
Т
Влияние выбора величины порога и исходных точек в простой схеме
кластеризации
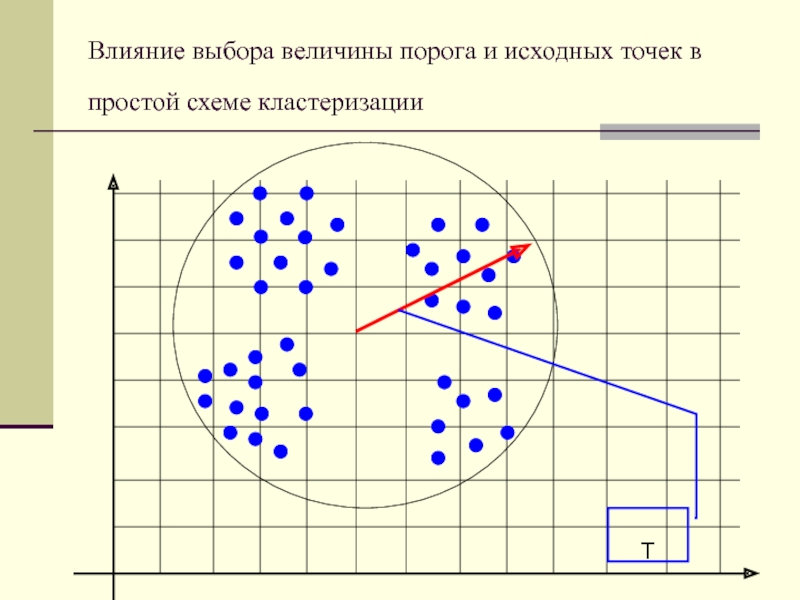
Слайд 8Т
Влияние выбора величины порога и исходных точек в простой схеме
кластеризации
Слайд 9Алгоритм обладает рядом очевидных недостатков, тем не менее он позволяет
быстро и просто получить приблизительные оценки основных характеристик заданного набора
данных.
Алгоритм привлекателен с вычислительной точки зрения, поскольку для выявления центра кластеров, соответствующих заданному порогу Т, ему требуется только однократный просмотр выборки.
Слайд 10Для того, чтобы процедура выполняла эффективную кластеризацию, необходимо выполнять большое
количество экспериментов, варьируя значения порогов и центров кластеров.
Важными характеристиками
эффективности проведённого эксперимента являются:
Расстояния разделяющие центры кластеров;
Количества образов вошедших в различные кластеры;
Ближайшая и наиболее удалённая от центра точки кластера;
Различие размеров отдельных кластеров.
Слайд 11Информацию, полученную после каждого цикла обработки данных , можно использовать
для коррекции:
Значения порога Т;
Новой исходной точки кластеризации.
Можно рассчитывать на
получение с помощью подобной процедуры полезных результатов, когда в данных имеются характерные «гнёзда», которые достаточно хорошо разделяются при соответствующем выборе значения порога.
Слайд 12Алгоритм максимина
Обучение без учителя
Слайд 13Алгоритм максиминного расстояния представляет собой ещё одну эвристическую процедуру, которая
использует евклидово расстояние.
Алгоритм аналогичен предыдущему, однако в первую очередь
он выявляет наиболее удалённые кластеры.
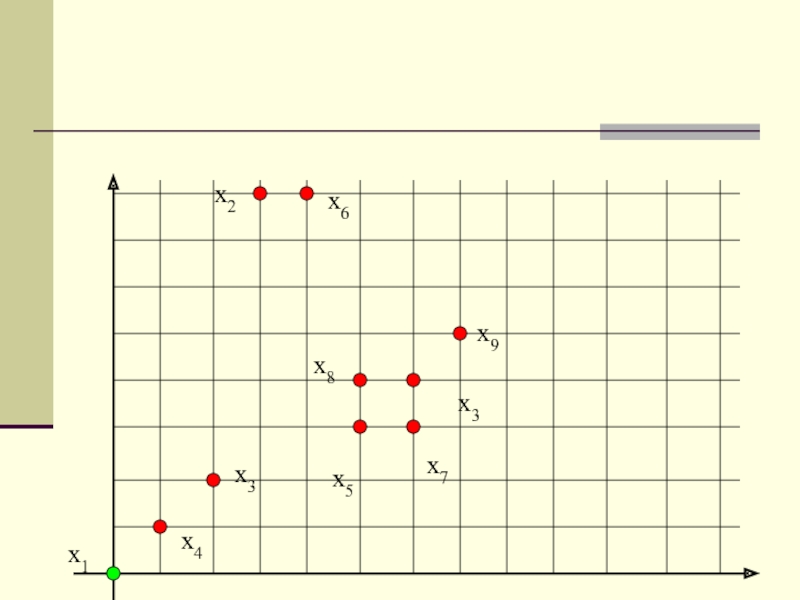
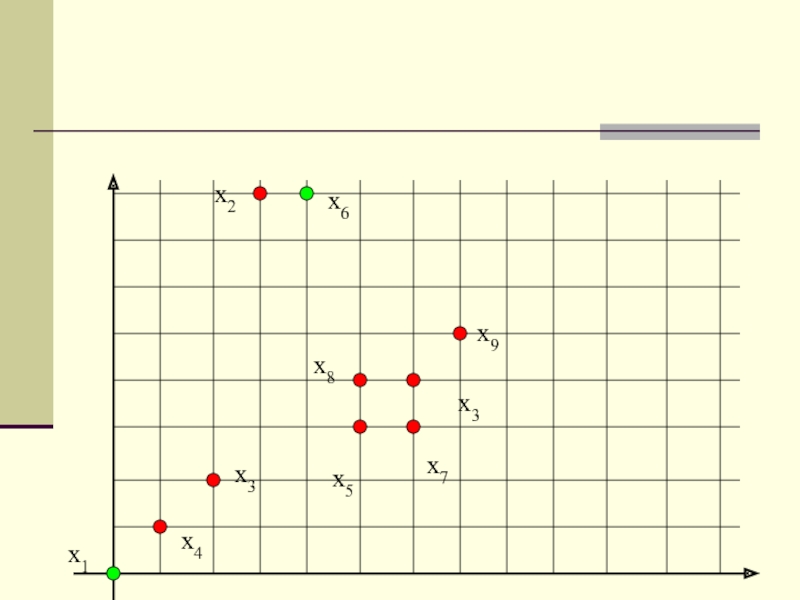
Рассмотрим алгоритм максиминного расстояния на примере:
Дана выборка из 10 двумерных образов рис.1.
Даны таблицы, в которых содержатся выборочные образы и центры кластеров, полученных в результате выполнения алгоритма (рис.2.).
Слайд 15Шаг 1. Выбор произвольным образом центра кластера. Пусть это будет
x1. См. табл.1.
Шаг 2. Вычисляем расстояния d1i(z1,xi). Отыскиваем образ, отстоящий
от образа x1 на наибольшее расстояние, а именно, находим max(d1i(z1,xi)). В данном случае это будет x6. Образ x6 назначается центром кластера z2.
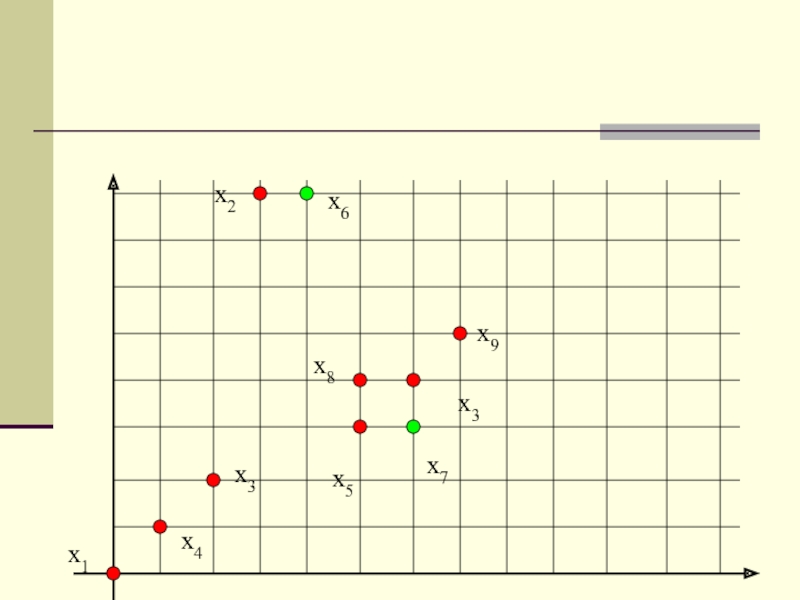
Шаг 3. Вычисляем расстояния между центрами кластеров z1 и z2 и всеми образами. В каждой паре этих расстояний вычисляем минимальное:
Слайд 17 gr=Minr(d(xr,z1), d(xr,z2)), r=1..(n-2);
Шаг 4. Находим максимальное расстояние из этих
минимальных:
L = Max(g1, g2,…, gn-2)
Если L > ½
d(z1,z2), то соответствующий образ назначается центром кластера z3;
В противном случае выполнение алгоритма прекращается. В приведённом примере центом кластера является образ x7.
Слайд 19Шаг 5. На следующем шаге вычисляются расстояния между тремя выделенными
кластерами и всеми остальными образами. В каждой группе из трёх
расстояний выбирается минимальное:
gr=Minr(d(xr,z1), d(xr,z2), d(xr,z3)), r=1..(n-3);
Шаг 6. На следующем шаге вычисляются максимальное из этих расстояний:
L = Max(g1, g2,…, gn-3)
Слайд 20Если L составляет большую часть «типичных» предыдущих максимальных состояний, то
соответствующий образ назначается центром кластера z4;
В противном случае выполнение
алгоритм прекращается.
Хорошей мерой оценки предыдущих максимальных расстояний является их среднее значение.
В конкретном примере, который мы рассматриваем, максимальным расстоянием оказалось расстояние между образами x1 и x3. Это расстояние не удовлетворяет принятому условию.
На данном шаге работа алгоритма прекращается.
Слайд 21В общем случае работа алгоритма прекращается, когда на определённом шаге
алгоритма максимальное расстояние не соответствует условию выделения нового кластера.
В
предыдущем примере было выделено три кластера x1, x6 и x7.
Классифицируемые образы относят к кластеру, центр которого для него ближайший.
Таким образом, в нашем примере были выделены три кластера:
{x1, x3, x4} {x2, x6} {x5 x7 x8 , x8, x9}
Слайд 23Алгоритм К внутригрупповых средних
Обучение без учителя
Слайд 24Шаг 1. Выбираются К исходных центров кластеров z1(1), z2(1),…, zК(1).
Этот выбор выполняется произвольно, обычно в качестве исходных центров используют
первые К результатов выборки из заданного множества образов.
Шаг 2. На к шаге итерации заданное множество образов {x} распределяется по к кластерам по следующему правилу:
x Sj(k), если ||x-zj(k)|| < ||x-zi(k)||,
для всех i=1,2,…, K, ij, где Sj(k) – множество образов, входящих в кластер с центром zj(k).
Слайд 25Если ||x-zj(k)|| = ||x-zi(k)||, то решение принимается произвольным образом.
Шаг 3.
На основе результатов шага 2 образуются центры новых кластеров zj(k+1),
j = 1,2,…,k); Центры образуются исходя из условия, что сумма квадратов расстояния между всеми образами и новым центром должна быть минимальна. Другими словами, новые центры кластеров выбираются таким образом, чтобы минимизировать показатель качества:
Jj = ||x-zj(k+1)||2 , x Sj(k), j = 1,2,…,k
Слайд 26Центр zj(k+1) является по сути дела выборочным средним, определенным по
множеству Sj(k). Следовательно, новые центры кластеров определяются по формуле:
zj(k+1)
= 1/Nj x, x Sj(k), j = 1,2,…,k , где Nj – число выборочных образов, входящих в множество Sj(k).
Шаг 4. Равенство zj(k+1) = zj(k) является при j = 1,2,…,k является условием сходимости алгоритма. При достижении этого условия алгоритм завершается. В противном случае алгоритм повторяется от шага 2.
Слайд 27Качество работы алгоритмов, основанных на вычислении К внутригрупповых средних, зависит
от:
Числа выбираемых центров кластеров;
От выбора исходных центров кластеров;
От последовательности осмотра
образов;
От геометрической особенности данных.
Приемлемых результатов можно ожидать, если данные представляют собой характерные «гроздья», отстоящие друг от друга на значительное расстояние.
Слайд 28Практическое применение этого метода потребует ряда экспериментов, связанных с:
Выбором различных
значений К;
Выбором исходного расположения центров кластеров.
Пример:
Шаг 1. Задаётся К=2 и
выбирается z1(1)= x1=(0,0)’, z2(1)= x2=(1,0)’.
Слайд 29x1
x19
x20
x2
x8
x11
x3
x4
x5
x9
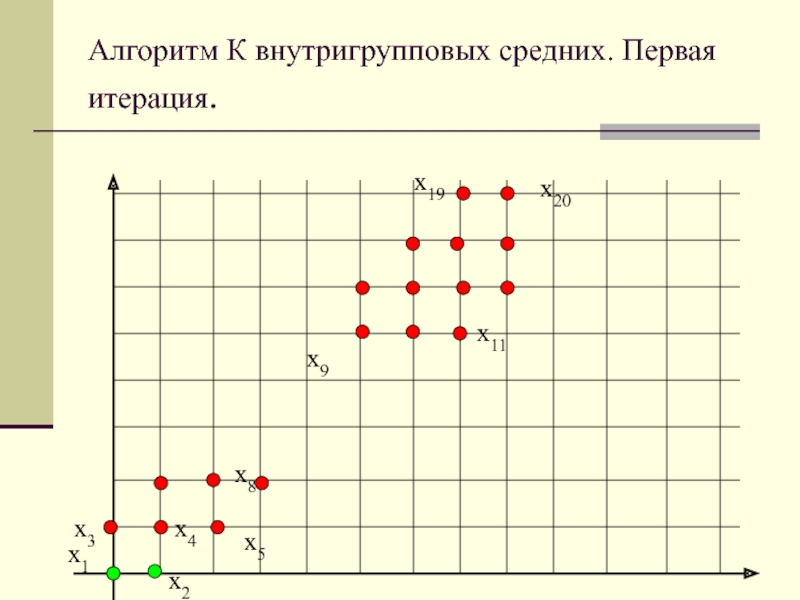
Алгоритм К внутригрупповых средних. Первая итерация.
Слайд 30Шаг 2. Поскольку ||x1-z1(1)|| < ||x1-zi(1)|| и ||x3-z1(1)|| < ||x1-zi(1)||,
i = 2, то S1(1) = {x1,x3}. Аналогичным образом устанавливаем,
что остальные образы расположены ближе к образу z2(1) и S2(1) = {x2,x4, x2,x5,…,x20}.
Шаг 3. Коррекция назначения центров кластеров:
Z1(2) = 1/N1 x, x S1(1) = ½ (x1+x3) = (0,0; 0,5)
Z2(2) = 1/N2 x, x S2(1) = 1/18 (x2+x4+…+x20) = (5,67; 5,33)
Слайд 31x1
x19
x20
x2
x8
x11
x3
x4
x5
x9
Алгоритм К внутригрупповых средних. Коррекция центров.
Слайд 32Шаг 4.Т.к. Z1(2) Z1(1), то возврат к шагу 2.
Шаг
2. Поскольку ||xl-z1(2)|| < ||xl-z2(2)||, l= 1,2,…,8 и ||xl-z2(2)||
||x1-z1(2)||, l = 9,10,…,20, то S1(2) = {x1,…,x8}. Аналогичным образом устанавливаем, что S2(2) = {x9,x10,…,x20}.
Шаг 3. Коррекция назначения центров кластеров:
Z1(3) = 1/N1 x, x S1(2) = 1/8 (x1+x2 +…+x8) = (1,25; 1,13)
Z2(3) = 1/N2 x, x S2(2) = 1/12 (x9+x10+…+x20) = (7,67; 7,33)
Слайд 33x1
x19
x20
x2
x8
x11
x3
x4
x5
x9
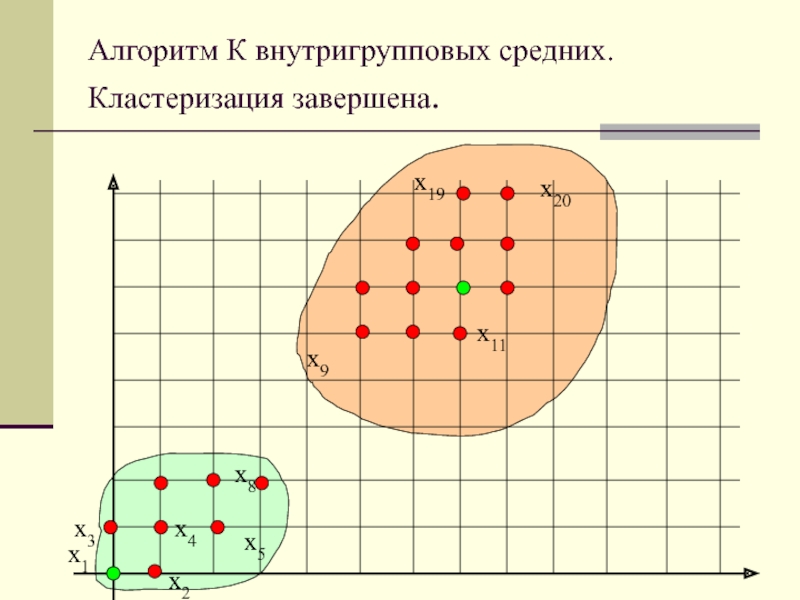
Алгоритм К внутригрупповых средних. Кластеризация завершена.
Слайд 34Шаг 4.Т.к. Z1(3) Z1(2), то возврат к шагу 2.
Шаг
2. Получаем те же самые результаты, что и на предыдущей
итерации: Z1(4) = Z1(3), Z2(4)= Z2(3).
Шаг 3. Коррекция назначения центров кластеров – получаем те же самые результаты.
Шаг 4.Т.к. Zj(4) Zj(3), j=1,2, алгоритм сошелся, получаем следующие центры кластеров:
Z1 = (1,25; 1,13)
Z2= (7,67; 7,33)