Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Описанная и вписанная окружности около треугольника
Содержание
- 1. Описанная и вписанная окружности около треугольника
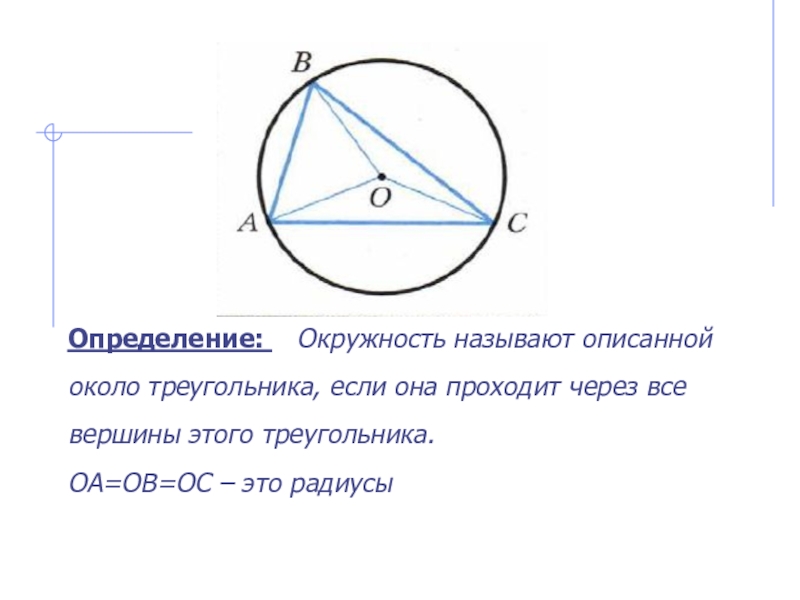
- 2. Определение: Окружность называют описанной около треугольника, если она проходит через все вершины этого треугольника.ОА=ОВ=ОС – это радиусы
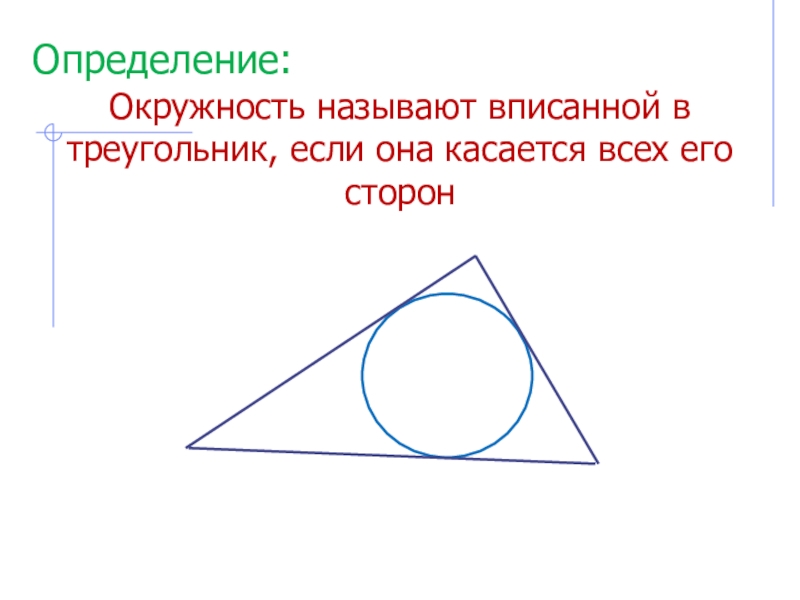
- 3. Окружность называют вписанной в треугольник, если она касается всех его сторонОпределение:
- 4. Теорема: Около любого треугольника можно описать окружность.
- 5. Практическая работа. Построить произвольный треугольник АВС. Провести
- 6. Около любого треугольника можно описать окружностьЗаметим, около
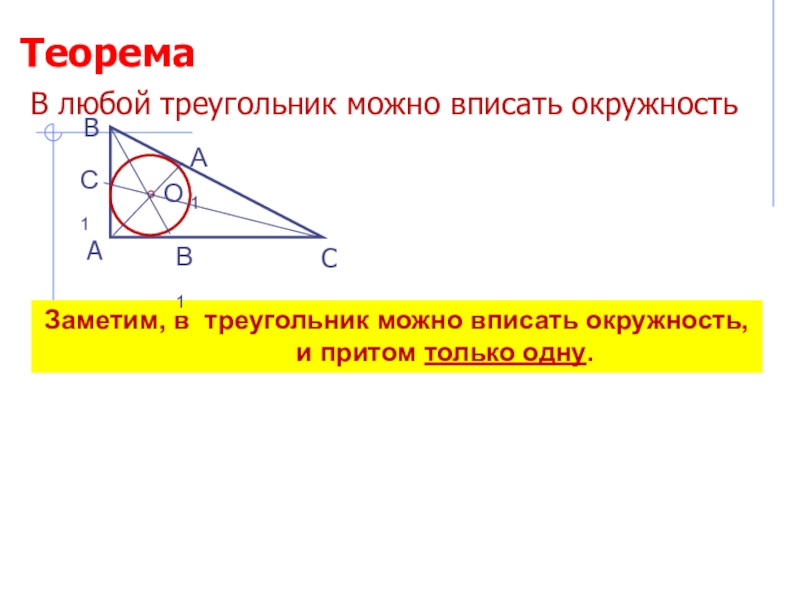
- 7. Заметим, в треугольник можно вписать окружность,
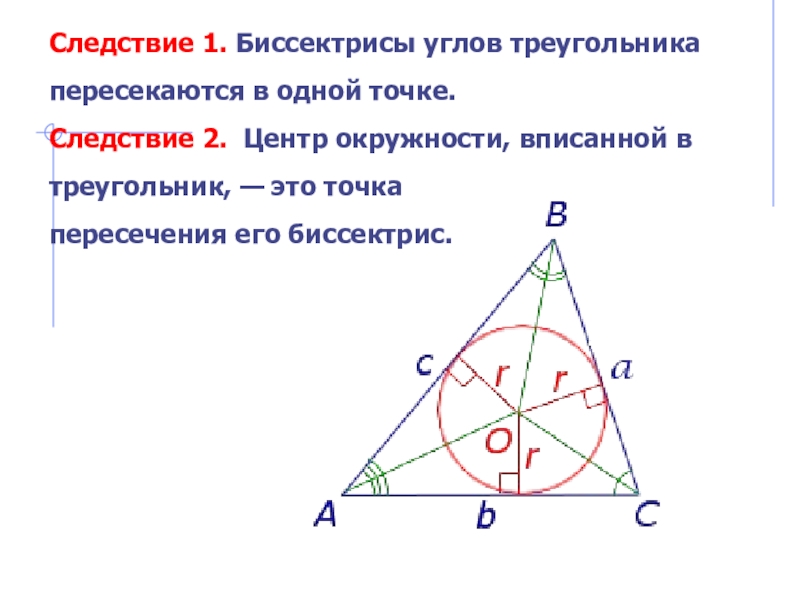
- 8. Следствие 1. Биссектрисы углов треугольника пересекаются в
- 9. 1) Какая окружность называется описанной около треугольника?2)
- 10. Скачать презентанцию
Определение: Окружность называют описанной около треугольника, если она проходит через все вершины этого треугольника.ОА=ОВ=ОС – это радиусы
Слайды и текст этой презентации
Слайд 2Определение: Окружность называют описанной около треугольника, если она проходит через все
вершины этого треугольника.
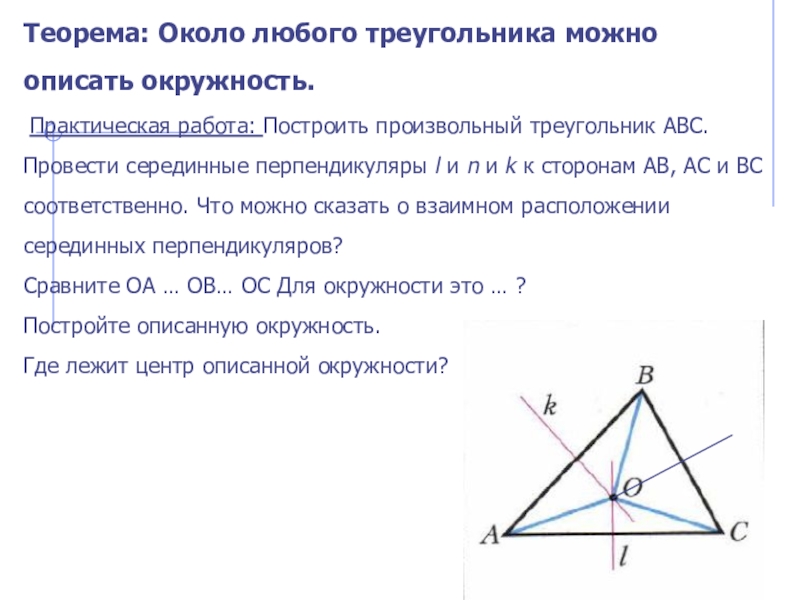
Слайд 4Теорема: Около любого треугольника можно описать окружность.
Практическая работа: Построить
произвольный треугольник АВС. Провести серединные перпендикуляры l и n и
k к сторонам АВ, АС и ВС соответственно. Что можно сказать о взаимном расположении серединных перпендикуляров?Сравните ОА … ОВ… ОС Для окружности это … ?
Постройте описанную окружность.
Где лежит центр описанной окружности?
Слайд 5Практическая работа. Построить произвольный треугольник АВС. Провести биссектрисы углов А,
В, С. Обозначить точку их пересечения буквой О.
Т. к.
точка О принадлежит биссектрисе угла А, то она … от сторон АВ и АС.Т.к. точка О принадлежит биссектрисе угла В, то она … от сторон ВА и ВС.
Т.к. точка О принадлежит биссектрисе угла С, то она … от сторон АС и ВС.
Следовательно, точка О равноудалена от всех сторон треугольника. Точка – это … окружности.
Расстояние от т. О до любой стороны треугольника – это … окружности
Теорема: В любой треугольник можно вписать окружность.
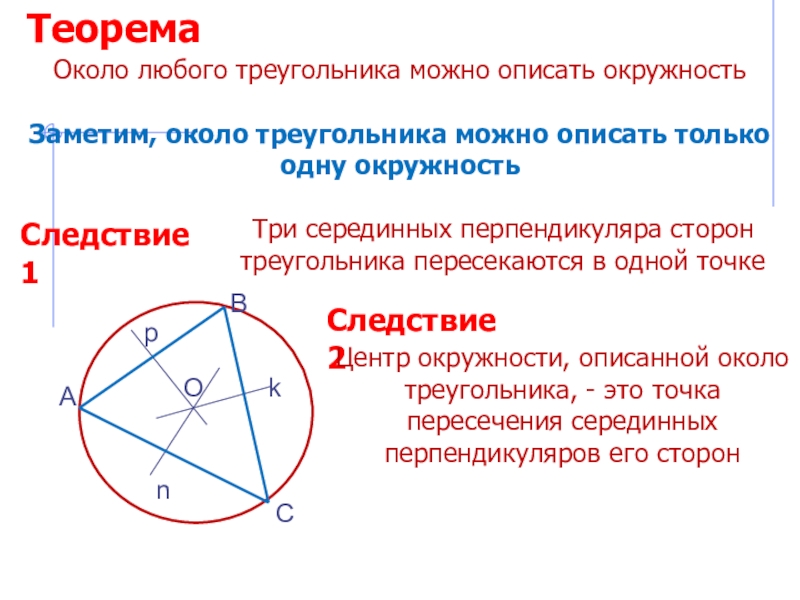
Слайд 6Около любого треугольника можно описать окружность
Заметим, около треугольника можно описать
только одну окружность
Теорема
Три серединных перпендикуляра сторон треугольника пересекаются в
одной точкеСледствие 1
Следствие 2
Центр окружности, описанной около треугольника, - это точка пересечения серединных перпендикуляров его сторон
Слайд 7Заметим, в треугольник можно вписать окружность,
и притом только одну.
О
С1
А1
В1
В любой треугольник можно
вписать окружностьТеорема
Слайд 8Следствие 1. Биссектрисы углов треугольника пересекаются в одной точке.
Следствие 2.
Центр окружности, вписанной в треугольник, — это точка
пересечения его биссектрис.
Слайд 91) Какая окружность называется описанной около треугольника?
2) Какой треугольник называют
вписанным в окружность?
3) Около какого треугольника можно описать окружность?
4) Какая
точка является центром окружности, описанной около треугольника?5) Какую окружность называют вписанной в треугольник?
6) Какой треугольник называют описанным около окружности?
7) В какой треугольник можно вписать окружность?
8) Какая точка является центром окружности, вписанной в треугольник?