Определение непрерывности функции в точке

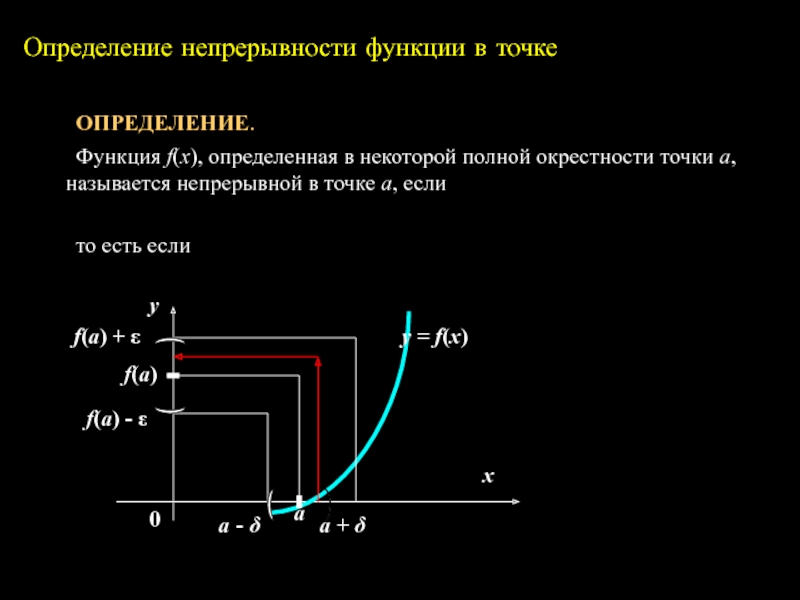
функций, непрерывных в точке
Теоремы о функциях, непрерывных на отрезке
Об

ограниченности непрерывной на отрезке функции
О достижимости точных граней функцией, непрерывной на отрезке

полной окрестности точки а, называется непрерывной в точке а, если

то

есть если

a

f(a)

a - δ

a + δ

f(a) + ε

f(a) - ε

x

y = f(x)

0

y

х = а + Δх. И непрерывность функции в точке

а означает, что приращение функции
f(а + Δх) – f(а) → 0 при Δх → 0.








ПРИМЕР.
Покажем, что функция f(x) = х2 непрерывна в любой точке а своей области определения.
Найдем приращение функции
f(а + Δх) – f(а) = (а + Δх)2 – а2 = 2аΔх + (Δх)2 → 0 при Δх → 0.
Следовательно, функция непрерывна в точке а.

a

a + Δx

x

f(a)

f(a + Δx)

0

y = f(x)

y

в точке а слева, если


ОПРЕДЕЛЕНИЕ.
Функция f(x), определенная в

правой полуокрестности точки а, называется непрерывной в точке а справа, если


ТЕОРЕМА.
Функция f(x), определенная в некоторой полной окрестности точки а, непрерывна в точке а тогда и только тогда, когда она непрерывна в этой точке слева и справа.

а. Точка а называется точкой разрыва функции в следующих случаях:
Функция

не определена в этой точке;
Функция определена в точке а, но

не существует

существует

Различают следующие три типа точек разрыва:

но функция не определена в этой точке или

то а называют точкой устранимого разрыва.
ПРИМЕРЫ.
1)

2) f(x) = (signx)2;

- 0) ≠ f (a + 0),
то это точка разрыва

первого рода.
Разность f (a +0) – f (a – 0) называется скачком функции в точке а.
ПРИМЕР.

бы один из односторонних пределов, то это точка разрыва второго

рода.

ПРИМЕР.

то существует такая окрестность этой точки, в которой функция ограничена.

Если

функция непрерывна в точке а и отлична от нуля, то существует такая окрестность этой точки, в которой функция сохраняет знак числа f (a).

Если функции f(x) и g(x) непрерывны в точке а, то их сумма, произведение и частное (если g(а) ≠ 0) непрерывны в этой точке.

4. Если функция z = f(y) непрерывна в точке yo , а функция y = ϕ(x) непрерывна в точке хо, причем yo= ϕ(xо), то в некоторой окрестности точки хо определена сложная функция f(ϕ(x)), непрерывная в точке хо.

свойств пределов функции.
Докажем свойство 4.
Возьмем произвольное число ε

> 0.
В силу непрерывности функции z = f(y) в точке yo найдется число


В силу непрерывности функции y = ϕ(x) в точке хо для найденного числа ρ найдется число


Итак,


Это значит, что, в силу определения непрерывности, функция f(ϕ(x)), определенная в окрестности точки хо, непрерывна в точке хо.

непрерывной на отрезке [a, b], если она непрерывна в каждой

внутренней точке отрезка, непрерывна в точке а справа, в точке b слева.

Множество функций, непрерывных на [a,b], обозначается как C[a,b].

Об ограниченности непрерывной на отрезке функции

ТЕОРЕМА (первая теорема Вейерштрасса)

Если f(x)∈C[a,b], то она ограничена на этом отрезке.

для любого числа n∈Ν найдется xn∈[a, b], такое что f(xn)

> n. Т.е. найдется такая последовательность значений аргумента {xn}, что соответствующая ей последовательность значений функции {f(xn)} будет бесконечно большой. Эта последовательность значений аргумента ограничена, значит, по теореме Больцано-Вейерштрасса, из нее можно выделить сходящуюся подпоследовательность, причем

В силу непрерывности функции

Но

как подпоследовательность бесконечно большой последовательности.
Полученное противоречие доказывает теорему.

отрезка. Например, функция f(x)=1/х непрерывна на (0, 1], но не

ограничена на этом интервале.
2) Теорема не верна для функции, разрывной на отрезке, например

1

1

x

y

0

теорема Вейерштрасса)
Если f(x)∈C[a, b], то она достигает на этом отрезке

своих точной нижней и верхней граней.

Доказательство.
Так как функция непрерывна на отрезке, то множество ее значений ограничено и, следовательно, имеет точную верхнюю и нижнюю грани. Пусть


Требуется доказать, что на отрезке найдутся точки, значения функции в которых равны m и М. Предположим, что f(x)< M во всех точках отрезка. Введем вспомогательную функцию

.

на этом отрезке, то есть существует С > 0, такое

что


откуда


То есть число М не является наименьшей из верхних граней, что противоречит определению точной верхней грани.
Следовательно, найдется такая точка х1∈[a,b], что f(x1)=М.


Аналогично доказывается для нижней грани.

Например, функция f(x)= х непрерывна на (0, 1), но не

достигает на этом интервале своих точных граней.
2) Теорема не верна для функции, разрывной на отрезке, например

x

y

1

1

0

0.5