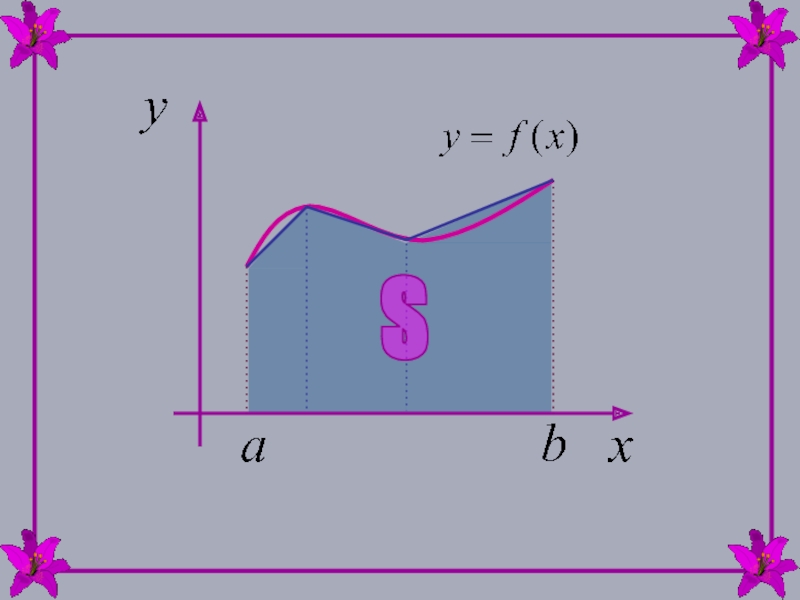
Требуется найти площадь криволинейной трапеции, ограниченной кривой y=f(x), прямыми x=a,
x=b и осью абсцисс y=0.Рассмотрим ломаную, расположенную достаточно близко к кривой.

![ОПРЕДЕЛЕННЫЙ
ИНТЕГРАЛ 1. ПОНЯТИЕ ОПРЕДЕЛЕННОГОИНТЕГРАЛАПусть на отрезке [a,b] задана неотрицательная функция y=f(x). Требуется 1. ПОНЯТИЕ ОПРЕДЕЛЕННОГОИНТЕГРАЛАПусть на отрезке [a,b] задана неотрицательная функция y=f(x). Требуется найти площадь криволинейной трапеции, ограниченной кривой](/img/thumbs/54e361770a7070606da75067d03794e7-800x.jpg)


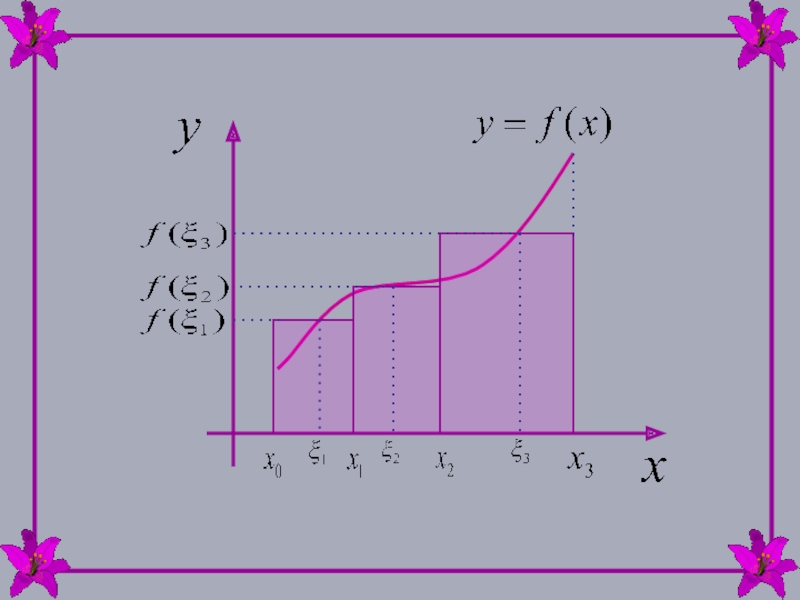
![ОПРЕДЕЛЕННЫЙ
ИНТЕГРАЛ Сумму вида называют интегральной суммой для функции y=f(x) на отрезке [a,b] . Сумму вида называют интегральной суммой для функции y=f(x) на отрезке [a,b] .](/img/thumbs/7d17b31165d68a65c1f4c31e51e5d90a-800x.jpg)


![ОПРЕДЕЛЕННЫЙ
ИНТЕГРАЛ Если существует конечный предел интегральной суммы при не зависящий от способа Если существует конечный предел интегральной суммы при не зависящий от способа разбиения отрезка [a,b] и выбора точек](/img/thumbs/969e12c9579868afedcea1b9b66cf038-800x.jpg)
![ОПРЕДЕЛЕННЫЙ
ИНТЕГРАЛ Функция y=f(x) называется интегрируемой на отрезке [a,b].Числа a и b называются нижним и верхним пределом, соответственно. Функция y=f(x) называется интегрируемой на отрезке [a,b].Числа a и b называются нижним и верхним пределом, соответственно.](/img/thumbs/de96f6775f2e98266a0c781582b84574-800x.jpg)


![ОПРЕДЕЛЕННЫЙ
ИНТЕГРАЛ Необходимое условие существованияопределенного интеграла2. СВОЙСТВА ОПРЕДЕЛЕННОГОИНТЕГРАЛАИнтегрируемая на отрезке [a,b] функция y=f(x) ограничена на этом отрезке. Необходимое условие существованияопределенного интеграла2. СВОЙСТВА ОПРЕДЕЛЕННОГОИНТЕГРАЛАИнтегрируемая на отрезке [a,b] функция y=f(x) ограничена на этом отрезке.](/img/tmb/3/279959/b644973eb703834174a3c7b14ce6674a-800x.jpg)
![ОПРЕДЕЛЕННЫЙ
ИНТЕГРАЛ Достаточное условие существованияопределенного интегралаЕсли на отрезке [a,b] функция y=f(x) непрерывна, то Достаточное условие существованияопределенного интегралаЕсли на отрезке [a,b] функция y=f(x) непрерывна, то она интегрируема на этом отрезке.](/img/tmb/3/279959/f5031e934d96a28c4df834f17a567cc7-800x.jpg)

![ОПРЕДЕЛЕННЫЙ
ИНТЕГРАЛ Доказательство:Пусть фиксировано разбиение отрезка [a,b] и выбор точек Рассмотрим интегральную сумму:Переходим Доказательство:Пусть фиксировано разбиение отрезка [a,b] и выбор точек Рассмотрим интегральную сумму:Переходим к пределу в левой и правой](/img/thumbs/be846dc1d8a001d5db2698071632cb07-800x.jpg)




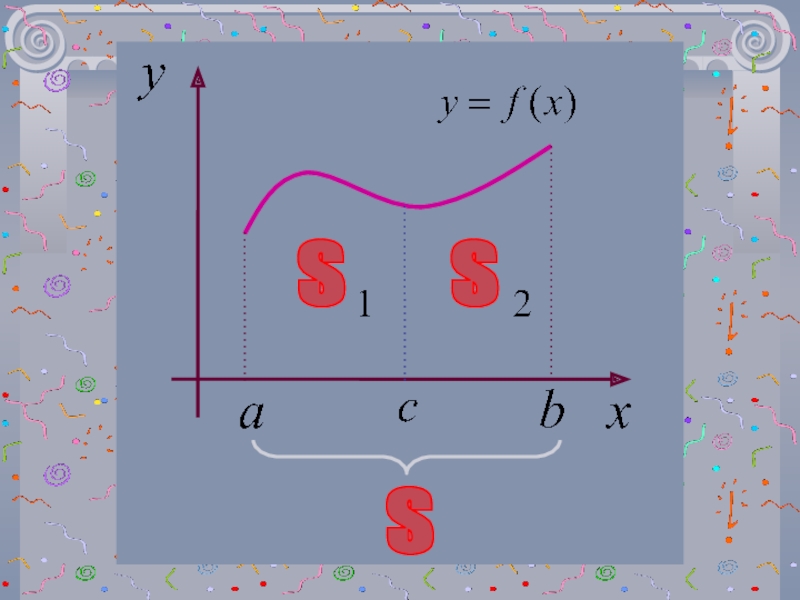
![ОПРЕДЕЛЕННЫЙ
ИНТЕГРАЛ 4Если на [a,b], где a 4Если на [a,b], где a](/img/tmb/3/279959/2acb502ccd250bccf246797e6600a37a-800x.jpg)
![ОПРЕДЕЛЕННЫЙ
ИНТЕГРАЛ Доказательство:Пусть фиксировано разбиение отрезка [a,b] и выбор точек то для интегральных Доказательство:Пусть фиксировано разбиение отрезка [a,b] и выбор точек то для интегральных сумм:ЕслиПереходим к пределу в левой и](/img/thumbs/a7e6b38acf3ddf828dddf87221f09bff-800x.jpg)
![ОПРЕДЕЛЕННЫЙ
ИНТЕГРАЛ Следствие.Пусть на [a,b], где a Следствие.Пусть на [a,b], где a](/img/thumbs/b9c8d5e8a795c199cb2b4b563a1057a5-800x.jpg)

![ОПРЕДЕЛЕННЫЙ
ИНТЕГРАЛ 5Если на [a,b], где a 5Если на [a,b], где a](/img/tmb/3/279959/deb8d7ae6f729a96905aeee96eeff6b5-800x.jpg)


![ОПРЕДЕЛЕННЫЙ
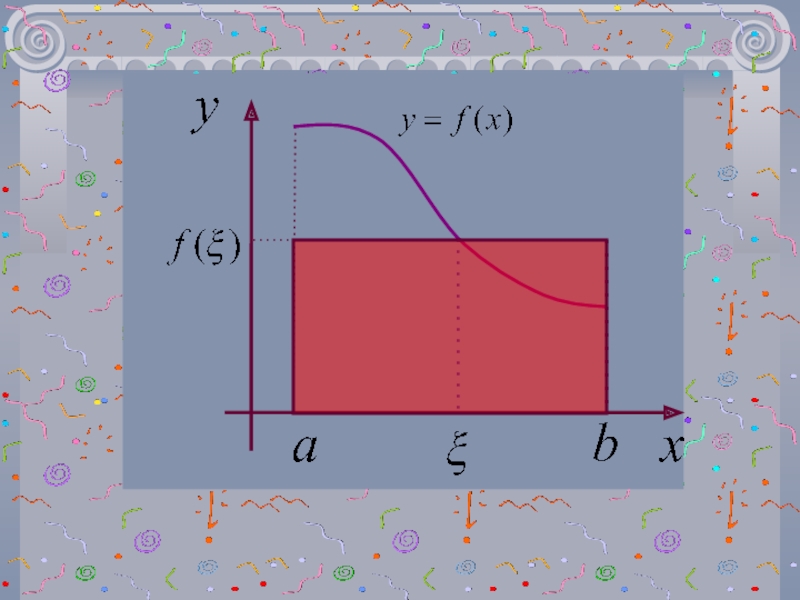
ИНТЕГРАЛ ПустьТогда теорема о среднем утверждает, что найдется такая точкачто площадь под ПустьТогда теорема о среднем утверждает, что найдется такая точкачто площадь под кривой y=f(x) на [a,b] равна площади](/img/thumbs/2a66d74737bc1f51fb48933e80943cb2-800x.jpg)

![ОПРЕДЕЛЕННЫЙ
ИНТЕГРАЛ 6Если на [a,b] функция y=f(x) неотрицательна, то площадь под этой кривой 6Если на [a,b] функция y=f(x) неотрицательна, то площадь под этой кривой численно равна определенному интегралуГеометрический смыслопределенного интеграла](/img/thumbs/97f5fe8aa12f684f3478971ee4f11962-800x.jpg)