Определители

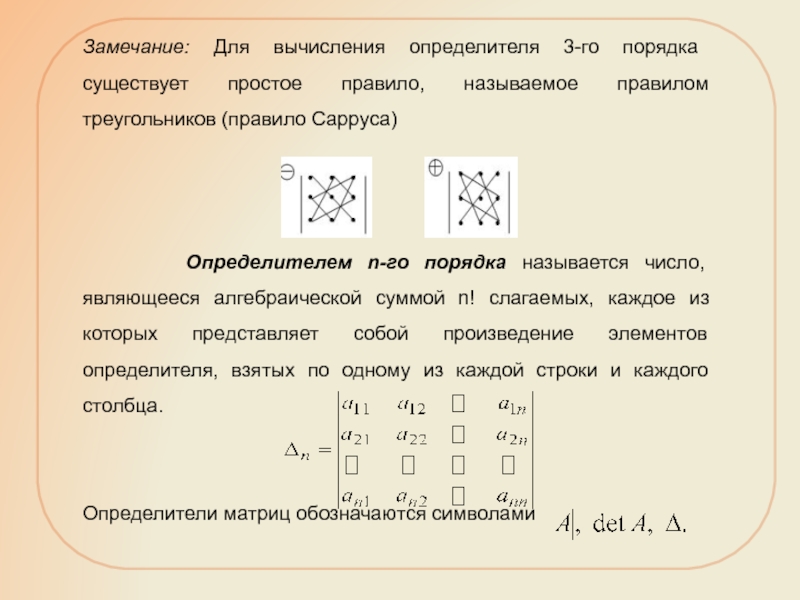
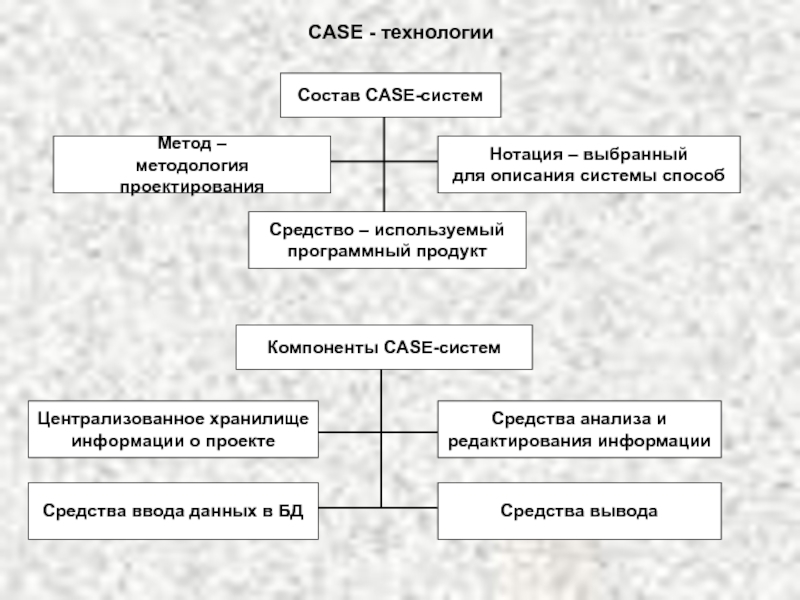
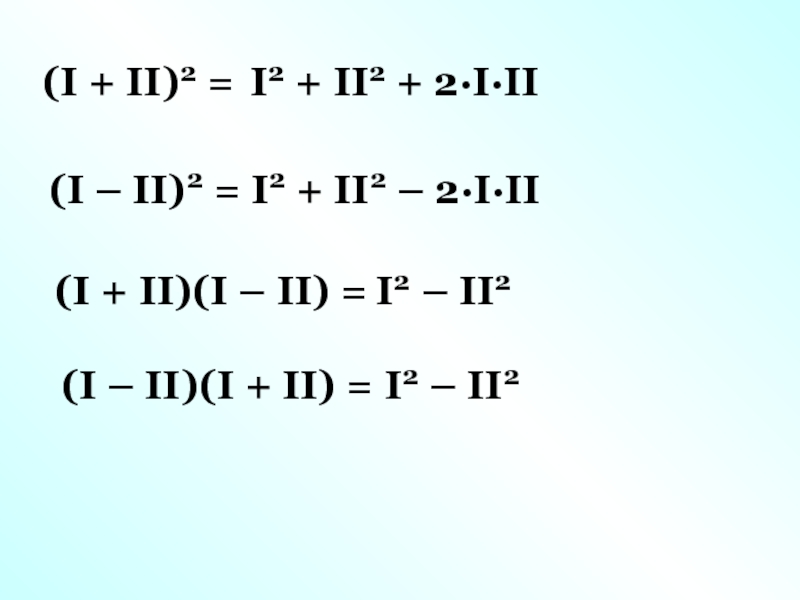уравнений с двумя неизвестными.


Определителем второго порядка

называется число, обозначаемое символом А и определяемое равенством:


Определителем третьего порядка называется число:





Числа называются элементами определителя, горизонтальные ряды элементов – строками, вертикальные – столбцами (i – номер строки, k – номер столбца).

правилом треугольников (правило Сарруса)



Определителем n-го порядка

называется число, являющееся алгебраической суммой n! слагаемых, каждое из которых представляет собой произведение элементов определителя, взятых по одному из каждой строки и каждого столбца.


Определители матриц обозначаются символами

.

на примере определителей третьего порядка.
1 Определитель не изменится при замене

всех его строк соответствующими столбцами.



2 При перестановке 2-х столбцов (строк) определитель меняет свой знак.


3 Определитель с 2-мя одинаковыми столбцами (строками) равен нулю.
4 Множитель, общий для элементов некоторого столбца (строки), можно вынести за знак определителя.

:

равен нулю.


6 Определитель с двумя пропорциональными столбцами (строками) равен нулю.



7

Если все элементы некоторого столбца (строки) представлены в виде суммы 2-х чисел, то весь определитель может быть представлен в виде суммы 2-х определителей.




8 Определитель не изменяется, если к элементам некоторой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.

Минором элемента определителя называется определитель, полученный

из данного вычеркиванием i-ой строки и k-го столбца.
Алгебраическим дополнением элемента называется его минор взятый со знаком : .
Теорема 1 (теорема Лапласа). Определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.


Теорема 2. Сумма произведений элементов какой-либо строки (столбца) на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю.

Замечание. Рассмотренные в этой лекции свойства справедливы и для определителей более высокого порядка, в частности теорема Лапласа позволяет вычислять определители любого порядка.

минором и алгебраическим дополнением?
Каковы способы вычисления определителей?
2. Вычислить определитель :




3.

Вычислить определитель:





4. Составить определитель третьего порядка, равный нулю.
5. Решите уравнение