возможных.
Задача оптимизации
Выбор оптимального решения производится с помощью некоторой зависимой от
параметров x1, x2, …, xn функции y=f(x1, x2, …, xn), которая называется целевой функцией.Задачи оптимизации делятся на:
а) безусловные, когда необходимо найти max/min целевой функции
б) условные, при постановке которых задаются некоторые условия (ограничения) в виде уравнений и неравенств.





![Оптимизация Интегрирование Постановка задачи. 1. Пусть функция f(x) непрерывна и дифференцируема на отрезке Постановка задачи. 1. Пусть функция f(x) непрерывна и дифференцируема на отрезке [a,b];Метод золотого сечения2. Функция f(x) имеет](/img/thumbs/678896187e41b1a6df8f0c88f46e8862-800x.jpg)
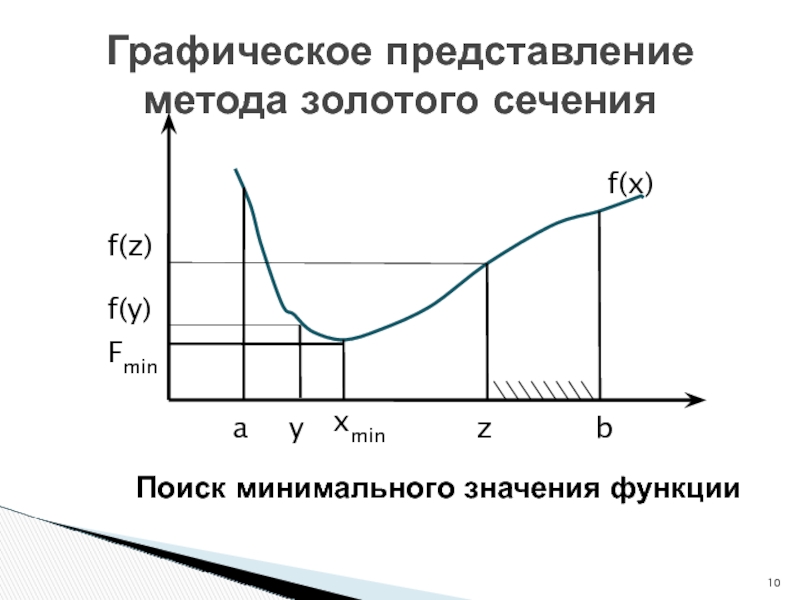
![Оптимизация Интегрирование 1. Разобьем интервал [a,b] на неравные части, используя золотое сечение. Найдем 1. Разобьем интервал [a,b] на неравные части, используя золотое сечение. Найдем точки y и z по формулам:Алгоритм](/img/thumbs/da22b97abca56e44e5ad222729b58f57-800x.jpg)



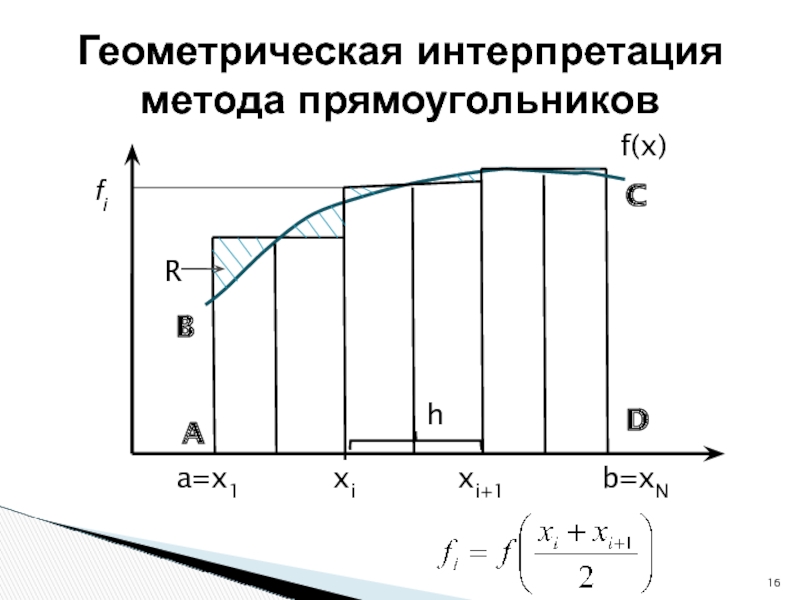
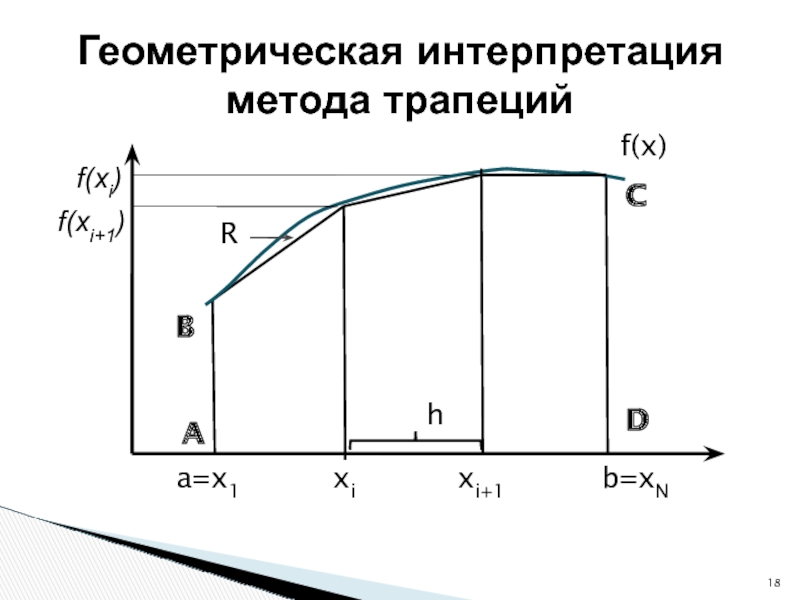
![Оптимизация Интегрирование Задача: Найти площадь криволинейной трапеции ABCD, ограниченной подынтегральной функцией f(x) и Задача: Найти площадь криволинейной трапеции ABCD, ограниченной подынтегральной функцией f(x) и пределами интегрирования [a,b].Численное интегрированиеРешение: Разбиваем интервал](/img/thumbs/d3b2775b9af5886a917bab2c5f146cae-800x.jpg)


![Оптимизация Интегрирование 1. Разобьем интервал [a,b] на N равных частей. Метод центральных прямоугольников2. 1. Разобьем интервал [a,b] на N равных частей. Метод центральных прямоугольников2. Найдем h – длину каждого i-того](/img/thumbs/9629f8ef56a652a337a32d83fffa787a-800x.jpg)