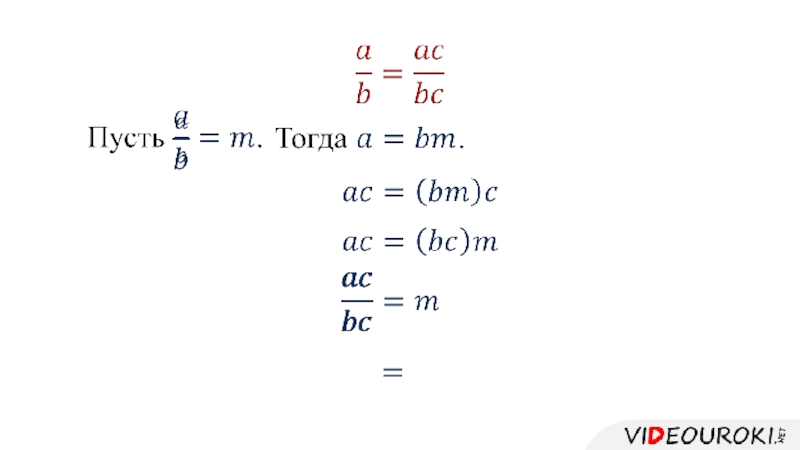Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основное свойство дроби. Сокращение дробей
Содержание
- 1. Основное свойство дроби. Сокращение дробей
- 2. ПланРабота с презентацией.Работа с учебником п.2, стр.10 -12. Задания из учебника переписать в тетрадь.Практическая часть: №40,41,42
- 3. Основное свойство дробиЕсли числитель и знаменатель дроби
- 4. Слайд 4
- 5. Основное свойство рациональной дроби:Если числитель и знаменатель
- 6. Тождеством называется равенство, верное при всех допустимых
- 7. Основное свойство рациональной дроби позволяет сокращать дроби и приводить дробь к новому знаменателю.Решение:а)б)в)
- 8. Решение:Дополнительный множительа)б)в)
- 9. Если числитель и знаменатель рациональной дроби умножить
- 10. Скачать презентанцию
ПланРабота с презентацией.Работа с учебником п.2, стр.10 -12. Задания из учебника переписать в тетрадь.Практическая часть: №40,41,42
Слайды и текст этой презентации
Слайд 2План
Работа с презентацией.
Работа с учебником п.2, стр.10 -12. Задания из
учебника переписать в тетрадь.
Слайд 3Основное свойство дроби
Если числитель и знаменатель дроби умножить или
разделить
на одно и то же число, отличное от нуля, то
значение дроби не изменится.
Деление числителя и знаменателя на одно и то же
число называется сокращением дроби.
Слайд 5Основное свойство рациональной дроби:
Если числитель и знаменатель рациональной дроби
умножить
на один и тот же ненулевой многочлен, то
получится равная
ей дробь.Если числитель и знаменатель рациональной дроби
разделить на один и тот же ненулевой многочлен, то
получится равная ей дробь.
тождество
Слайд 6Тождеством называется равенство, верное при всех
допустимых значениях входящих в
него переменных.
Два выражения, принимающие равные значения при
всех допустимых значениях
переменных, называются тождественно равными.
Замену одного такого выражения другим называют
тождественным преобразованием выражения.
тождество
Слайд 7Основное свойство рациональной дроби позволяет
сокращать дроби и приводить дробь
к новому знаменателю.
Решение:
а)
б)
в)
Слайд 9Если числитель и знаменатель рациональной дроби умножить
на один и
тот же ненулевой многочлен, то получится равная
ей дробь.
Если числитель
и знаменатель рациональной дроби разделить на один и тот же ненулевой многочлен, то получится равная
ей дробь.
Основное свойство рациональной дроби позволяет сокращать
дроби и приводить дробь к новому знаменателю.
Повторим главное:
