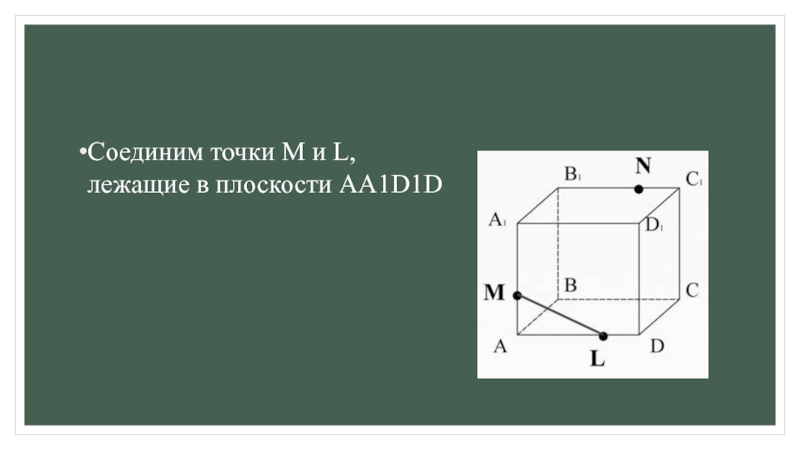
одной плоскости;
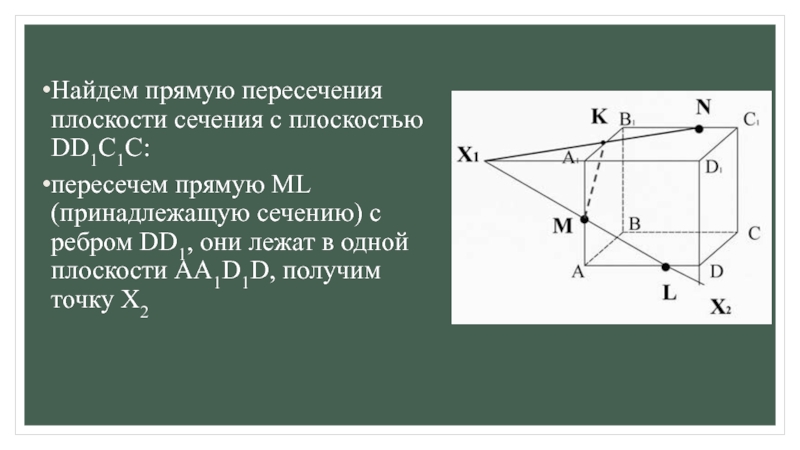
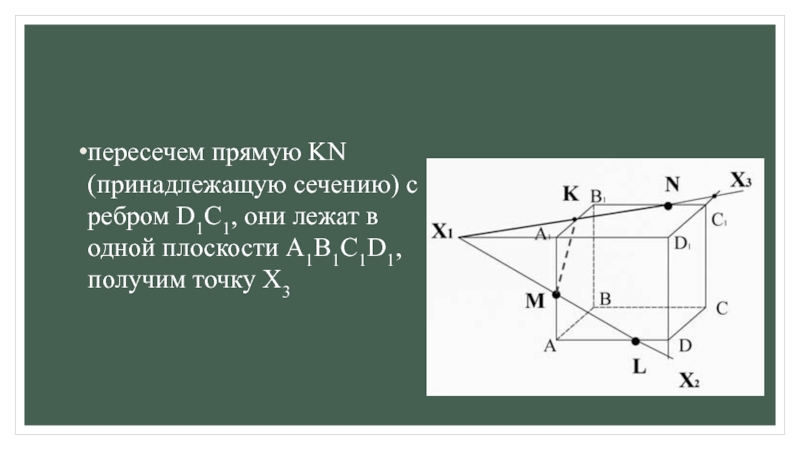
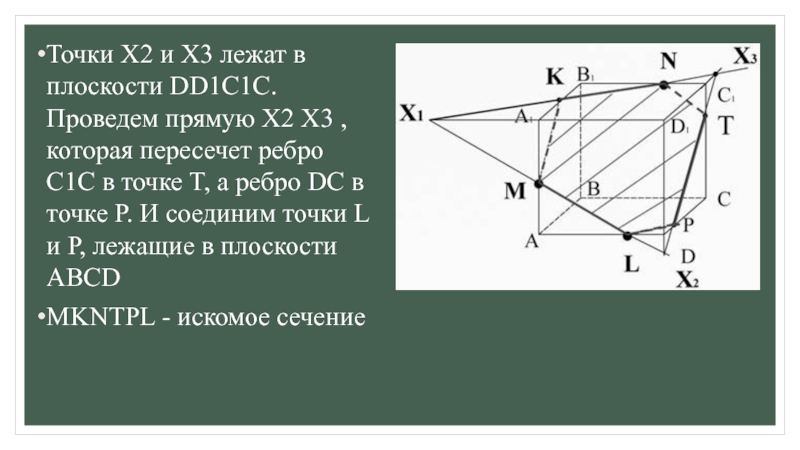
2) ищем прямые пересечения плоскости сечения с гранями многогранника,
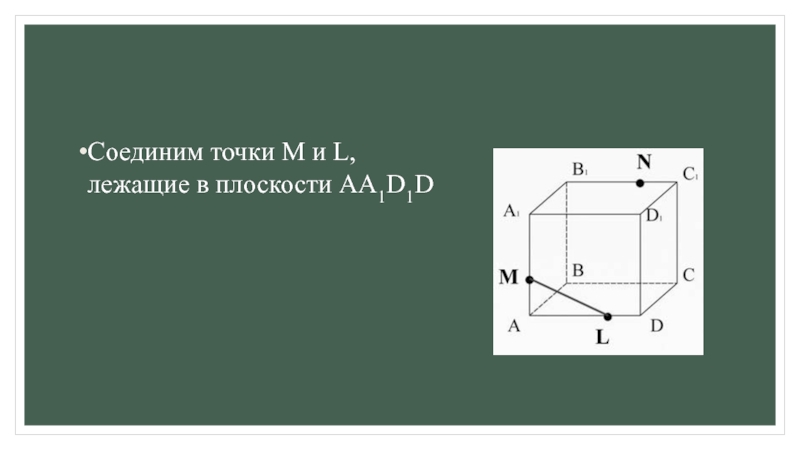
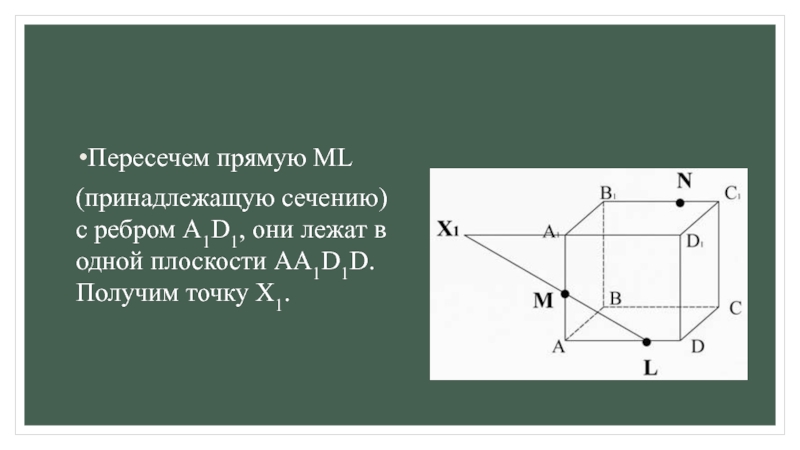
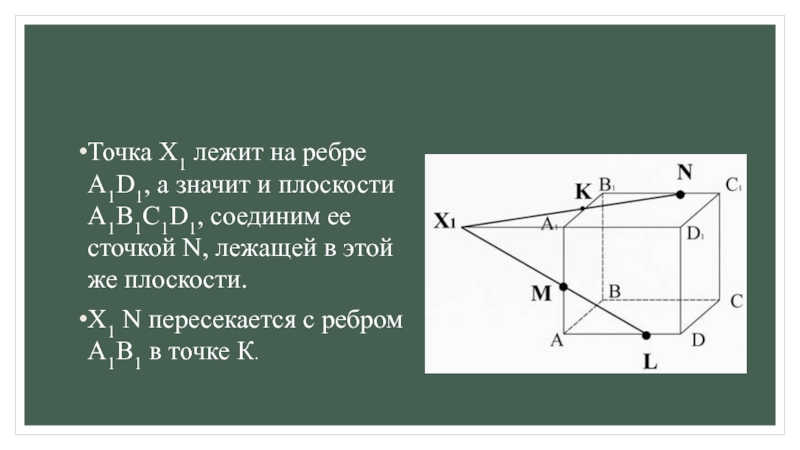
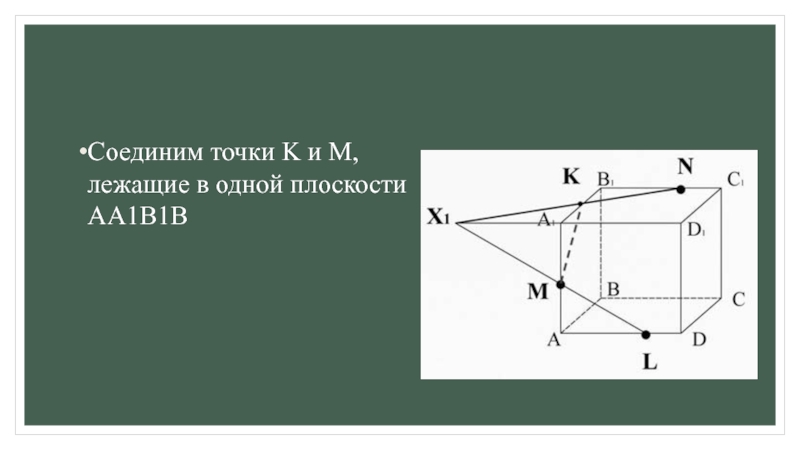
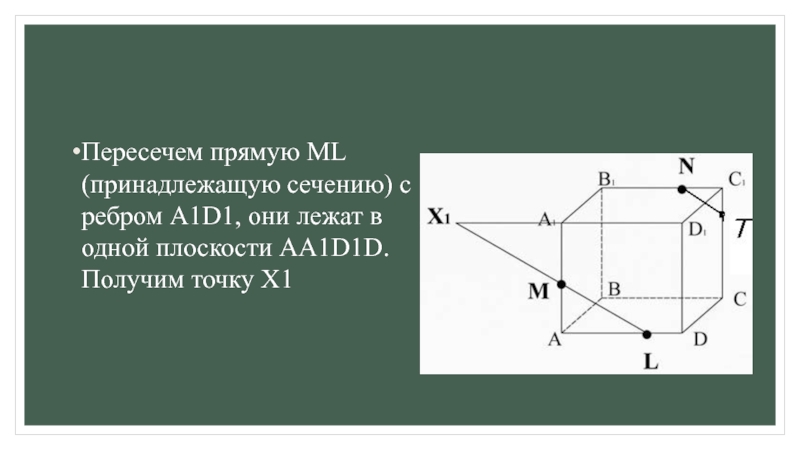
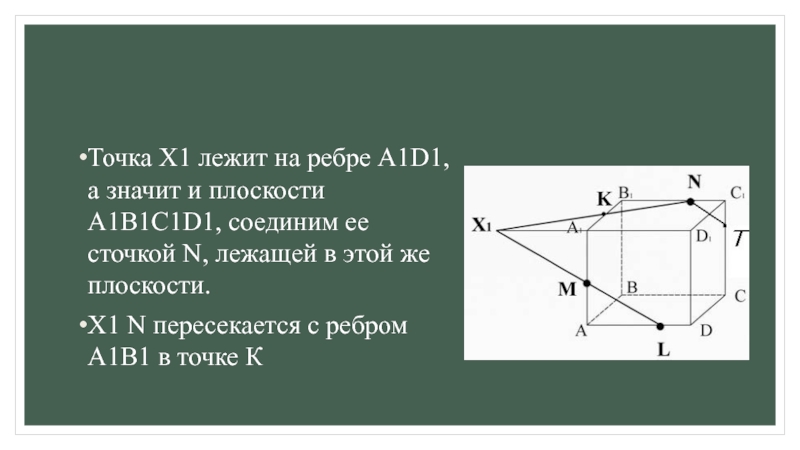
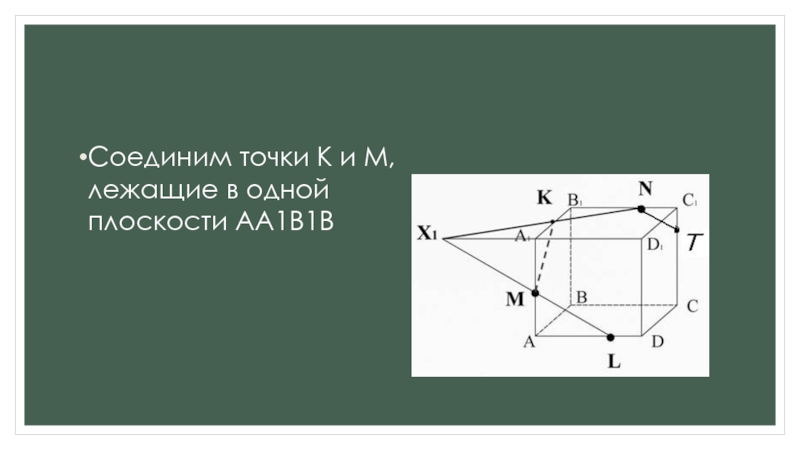
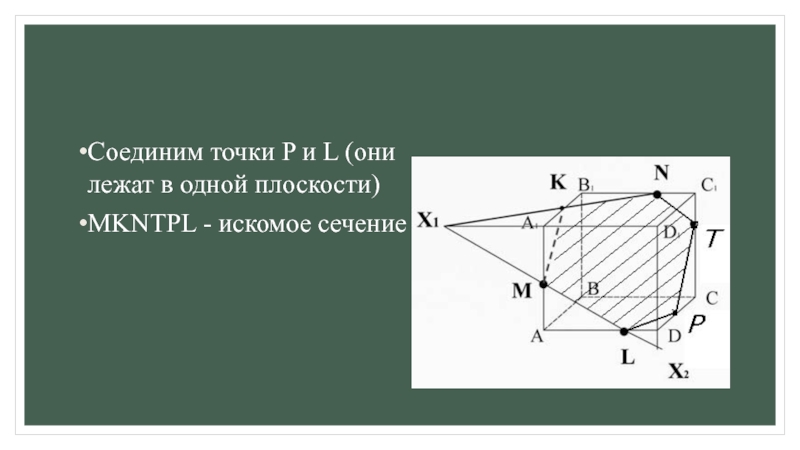
для этогоа) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);
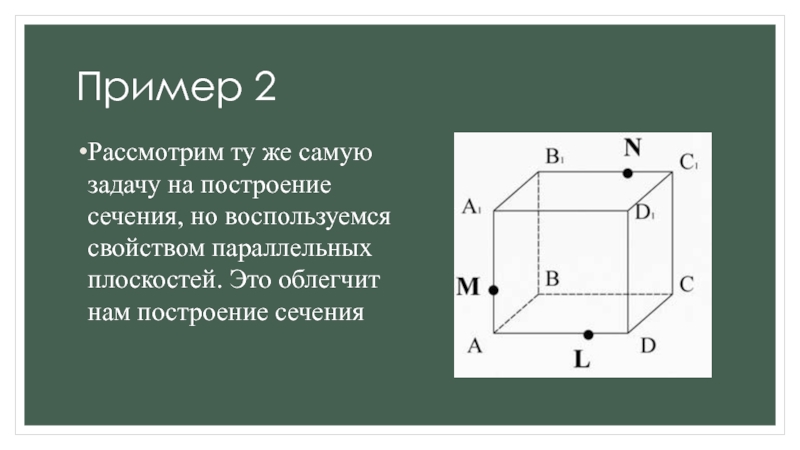
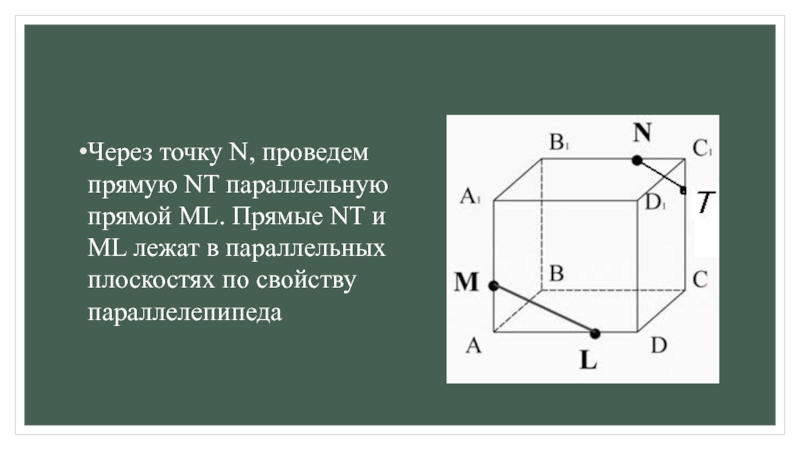
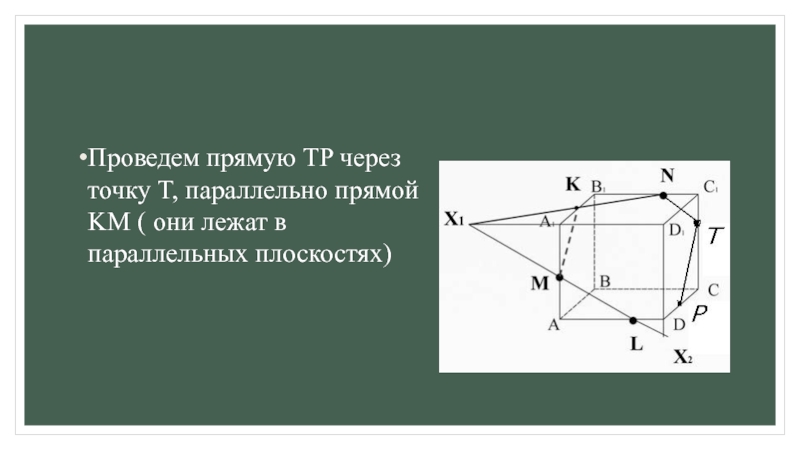
б) параллельные грани плоскость сечения пересекает по параллельным прямым.