Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основные теоремы теории вероятностей
Содержание
- 1. Основные теоремы теории вероятностей
- 2. Размещения Теорема: число размещений из n
- 3. 1) Студенты изучают 6 различных дисциплин. Если
- 4. Перестановки Перестановкой из n элементов называется любое
- 5. Записать все возможные перестановки для чисел 3,5,73,5,7
- 6. Сочетания Сочетанием из n элементов по m
- 7. 1) Имеется 10 белых и 5 черных
- 8. Правило умноженияЕсли требуется выполнить одно за другим
- 9. Правило сложения Если два действия взаимно исключают
- 10. Основные понятияСобытия А и В называются несовместными,
- 11. Пусть А и В - события, связанные
- 12. Слайд 12
- 13. Слайд 13
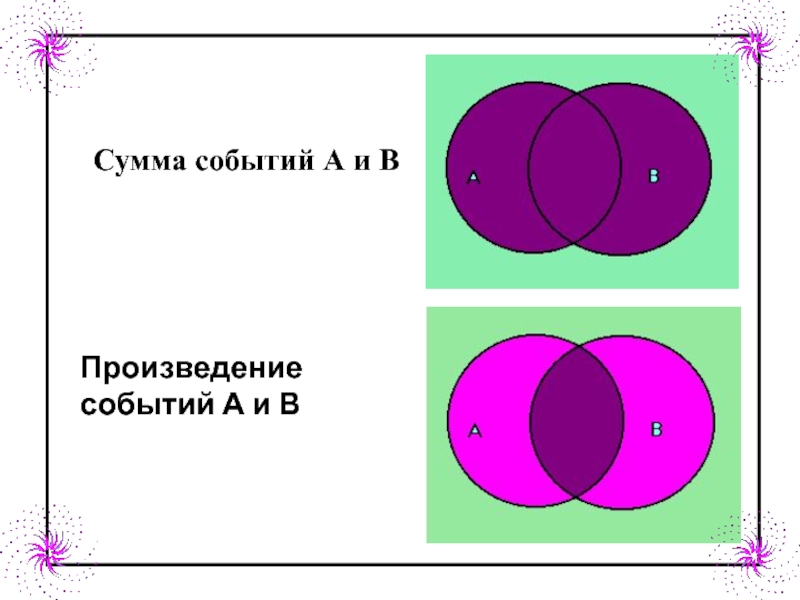
- 14. Сумма событий А и ВПроизведение событий А и В
- 15. Событие А - попадание при первом выстреле,
- 16. Пусть событие А1 - попадание в цель
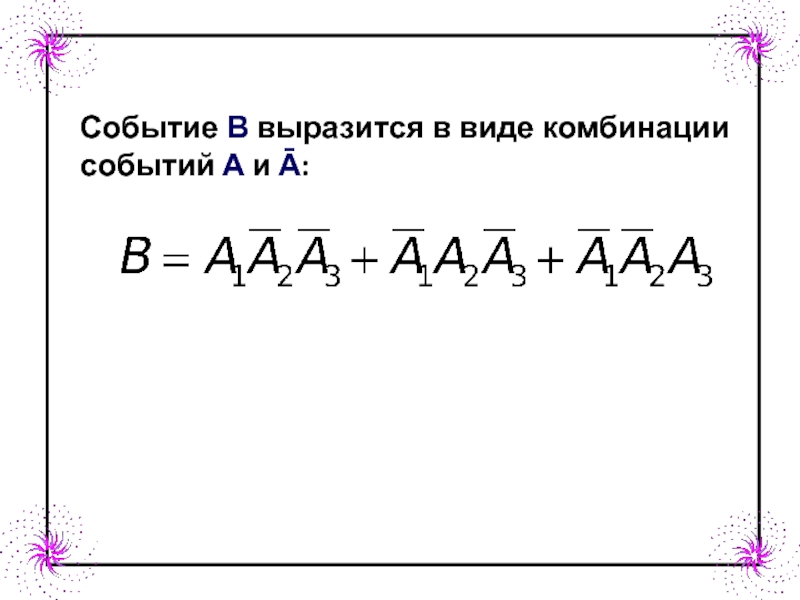
- 17. Событие В выразится в виде комбинации событий А и Ā:
- 18. ТЕОРЕМА О СЛОЖЕНИИ ВЕРОЯТНОСТЕЙВероятность суммы двух несовместных событий А и В равна сумме вероятностей этих событийР(А+В)=Р(А)+Р(В)
- 19. Пусть все возможные исходы опыта сводятся к
- 20. Так как события А и В несовместны,
- 21. Следовательно, событию А+В будет благоприятно m+k случаев.
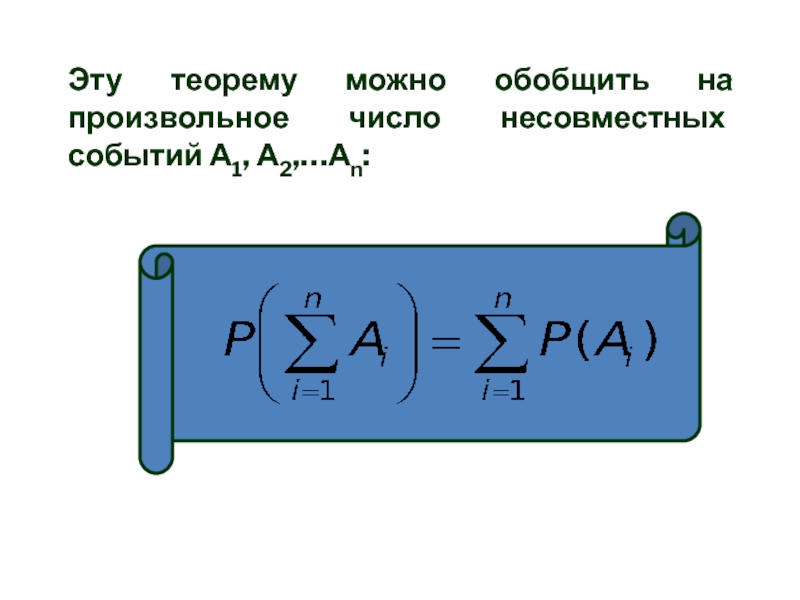
- 22. Эту теорему можно обобщить на произвольное число несовместных событий А1, А2,…Аn:
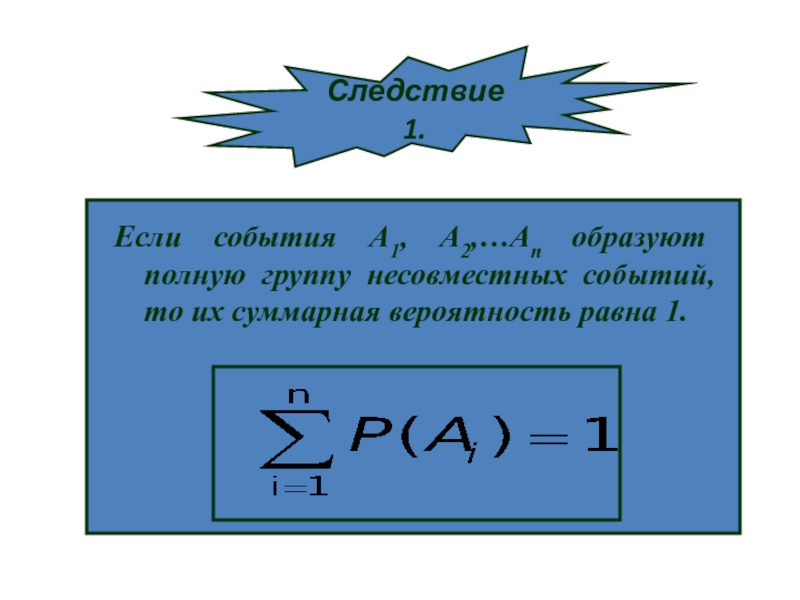
- 23. Если события А1, А2,…Аn образуют полную группу несовместных событий, то их суммарная вероятность равна 1.Следствие 1.
- 24. Так как события А1, А2,…Аn образуют полную
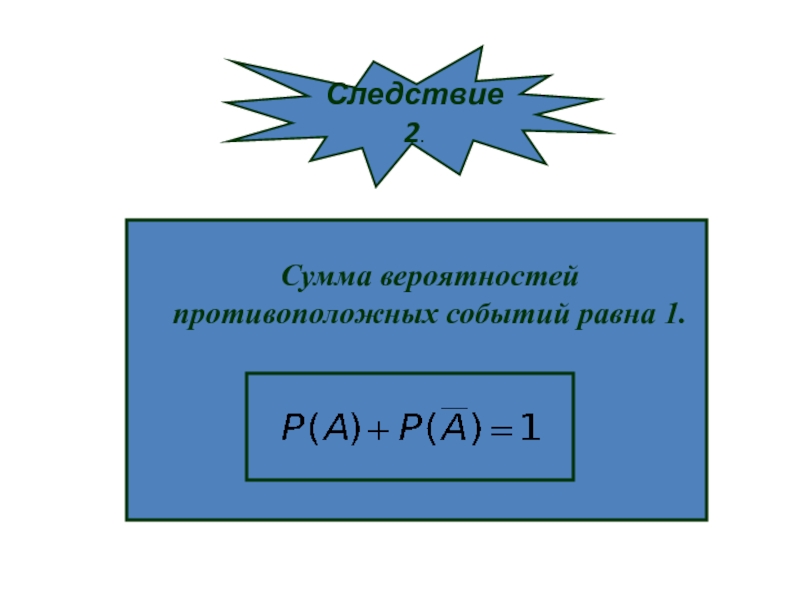
- 25. Сумма вероятностей противоположных событий равна 1.Следствие 2.
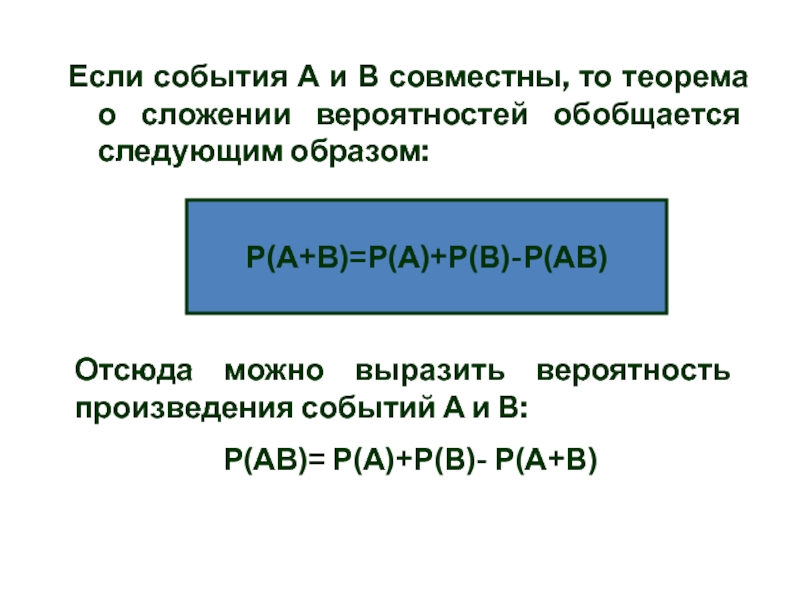
- 26. Если события А и В совместны, то
- 27. Пример 1.
- 28. События А и В будут совместными. Поэтому
- 29. Р(А)=0.4, Р(В)=0.2, Р(АВ)=0.1Следовательно,
- 30. Пример 2.Молодой человек рассматривает три возможности уклониться
- 31. Решение.Пусть событие А заключается в том, что
- 32. Так как Р(А)=0.5Р(В)=0.2Р(С)=0.01тоР(А+В+С)=0.5+0.2+0.01=0.7
- 33. Теорема умножения вероятностей. Условная вероятность Условной вероятностью
- 34. Теорема умножения вероятностей. Условная вероятностьВероятность совместного наступления
- 35. Формула полной вероятности является следствием теорем о
- 36. По теореме об умножении вероятностейОтсюда вытекает формула
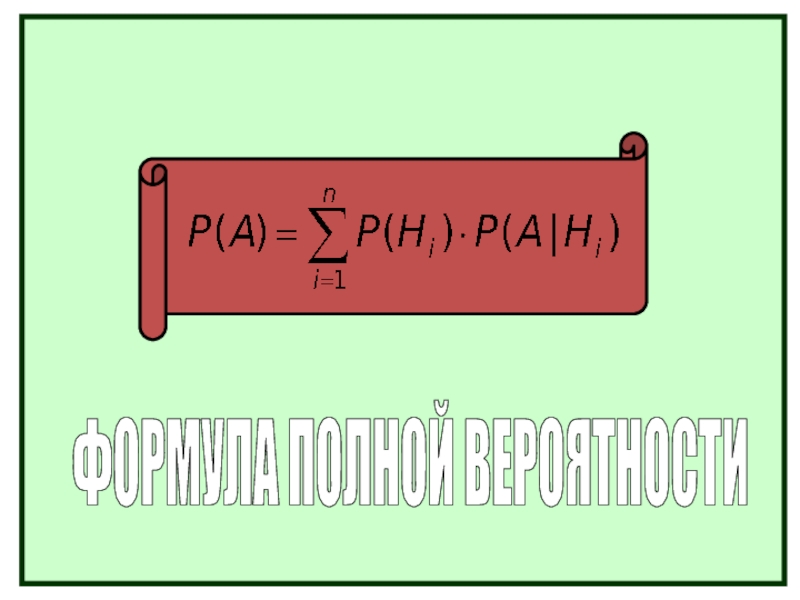
- 37. Формула полной вероятности. Вероятность события А,
- 38. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ
- 39. Студент, выйдя из дома за 30 минут
- 40. Н1- студент поехал автобусом;Н2- студент поехал троллейбусом;Н3-
- 41. Так как гипотезы образуют полную группу событий,
- 42. Слайд 42
- 43. Формула полной вероятности. Рассмотрим события В1,
- 44. ТЕОРЕМА ГИПОТЕЗ (ФОРМУЛА БАЙЕСА)Пусть имеется полная группа
- 45. Определим условные вероятности каждой из гипотез Р(Нi/А).По теореме об умножении вероятностей:ОтсюдаПо формуле полной вероятности
- 46. ФОРМУЛА БАЙЕСА
- 47. Формула БайесаРассмотрим событие А которое может наступить
- 48. Перед экзаменом студент с равной вероятностью может
- 49. Н1- достал шпаргалку из ботинка;Н2- достал шпаргалку
- 50. Т.е. требуется определить условную вероятность первой гипотезы,
- 51. ТогдаУсловные вероятности события А для каждой из гипотез даны по условию задачи:Р(А|Н1)=0.4; Р(А|Н2)=0.6; Р(А|Н3)=0.55
- 52. ПРИМЕР 2.Статистика запросов кредитов в банке: 10
- 53. Гипотезами в этой задаче будут:Н1- кредит взял
- 54. Условные вероятности события А для каждой из
- 55. Формула Бернулли Вероятность того что в n
- 56. Если производится n независимых опытов, в каждом
- 57. Известно, если монета упадет орлом, студент идет
- 58. Решение:Тогда вероятность противоположного события составит q=3/4.
- 59. Чтобы найти вероятность того, что при 5
- 60. Тогда вероятность искомого события составит
- 61. Асимптотические формулы Если число испытаний велико, то
- 62. Асимптотические формулы. Распределение ПуассонаЕсли вероятность события в
- 63. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Размещения
Теорема: число размещений из n по m
равно
упорядоченное подмножество из m элементов множества, состоящего из n различных элементовСлайд 31) Студенты изучают 6 различных дисциплин. Если ежедневно в расписание
включается по три дисциплины, то сколькими различными способами могут быть
распределены уроки в день?2)Сколько можно записать четырехзначных чисел , используя без повторения все десять цифр?
Слайд 4Перестановки
Перестановкой из n элементов называется любое упорядоченное множество, в
которое входят по одному разу все n различных элементов данного
множестваТеорема: Число перестановок n различных элементов равно n!
Слайд 5Записать все возможные перестановки для чисел 3,5,7
3,5,7 ; 3,7,5 ;
5,3,7 ; 5,7,3 ; 7,3,5 ; 7,5,3
2) Сколькими способами можно
расставить десять различных книг на полке, чтобы определенные четыре книги стояли рядом?Слайд 6Сочетания
Сочетанием из n элементов по m называется любое подмножество
из m элементов, которые принадлежат множеству, состоящему из n различных
элементовТеорема: Число сочетаний из n по m равно
Следствие: Число сочетаний из n элементов по n-m равно числу сочетаний из n элементов по m
Слайд 71) Имеется 10 белых и 5 черных шаров. Сколькими способами
можно выбрать 7 шаров , что бы среди них были
3 черных ?Решение: среди выбранных шаров 4 белых и 3 черных.
Способов выбора былых шаров
Способов выбора черных шаров
По правилу умножения искомое число способов равно
2) Сколькими способами можно группу из 12 человек разбить на две подгруппы, в одной из которых должно быть не более 5 , а во второй-
не более 9 человек ?
Выбор первой подгруппы однозначно определяет вторую, по правилу сложения искомое число способов равно:
Подгруппа из 3 человек
Подгруппа из 4 человек
Подгруппа из 5 человек
Слайд 8Правило умножения
Если требуется выполнить одно за другим какие то K
действий при чем 1 действие можно выполнить а1 способами, 2
действие – а2 способами, и так до K-го действия , которое можно выполнить ак способами, то все K действий вместе могут быть выполнены а1 · а2 · а3 …ак способами.4 мальчика 4 девочки садятся на 8 расположенных подряд стульев, причем мальчики садятся на места с четными номерами, а девочки – на места с нечетными номерами. Сколькими способами это можно сделать ?
Первый мальчик может сесть на любое из четырех четных мест, второй - на любое из оставшихся трех мест, третий – на любое оставшихся двух мест. Последнему мальчику предоставляется всего одна возможность. Согласно правилу умножения, мальчики могут занять четыре места 4·3·2·1=24 способами. Столько же возможностей имеют и девочки. Таким образом, согласно правилу умножения, мальчики и девочки могут занять все стулья 24 · 24=576 способами.
Слайд 9Правило сложения
Если два действия взаимно исключают друг друга, при
чем одно из них можно выполнить m способами, а другое
– n способами, то выполнить одно любое из этих действий можно m+n способами.Это правило легко распространить на любое конечное число действий
Слайд 10Основные понятия
События А и В называются несовместными, если в результате
данного испытания появление одного из них исключает появление другого (
испытание: стрельба по мишени ; А-выбивание четного числа очков; В- не четного).События А и В называются совместным, если в результате данного испытания появление одного из них не исключает появление другого( А- в аудиторию вошел учитель; В- вошел студент).
Если группа событий такова, что в результате испытания обязательно должно произойти хотя бы одно из них и любые два из них несовместны, то эта группа событий называется полной группой событий.
События называются равновозможными , если по условию испытания нет оснований считать какое-либо из них более возможным, чем любое другое ( А-орел; В-решка).
Слайд 11Пусть А и В - события, связанные с каким-либо опытом.
ОПЕРАЦИИ
НАД СОБЫТИЯМИ
Пример: выпадение герба при бросании монеты - событие, противоположное
выпадению решки.Событие называется противоположным
событию А, если оно происходит только
тогда, когда не происходит событие А.
Ā - событие, противоположное событию А.
Слайд 15Событие А - попадание при первом выстреле, событие В -
попадание при втором выстреле.
Событие А+В - хотя бы одно попадание.
Событие
АВ - попадание при обоих выстрелах.Пример.
Слайд 16Пусть событие
А1 - попадание в цель при первом выстреле;
Ā1
- промах при первом выстреле;
А2 - попадание в цель при
втором выстреле;Ā2 - промах при втором выстреле;
А3 - попадание в цель при третьем выстреле;
Ā3 - промах при третьем выстреле;
Рассмотрим событие В - в результате трех выстрелов состоялось одно попадание в цель.
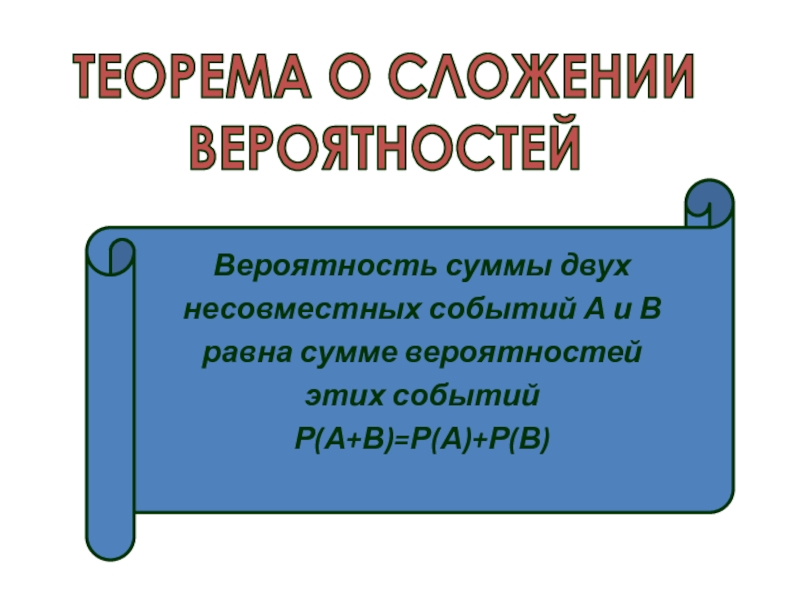
Слайд 18ТЕОРЕМА О СЛОЖЕНИИ
ВЕРОЯТНОСТЕЙ
Вероятность суммы двух
несовместных событий А и В
равна сумме вероятностей
этих событий
Р(А+В)=Р(А)+Р(В)
Слайд 19Пусть все возможные исходы опыта сводятся к n случаям, из
которых m случаев благоприятны событию А, а k - случаев
благоприятны событию В.Тогда вероятности событий А и В будут равны соответственно:
Доказательство:
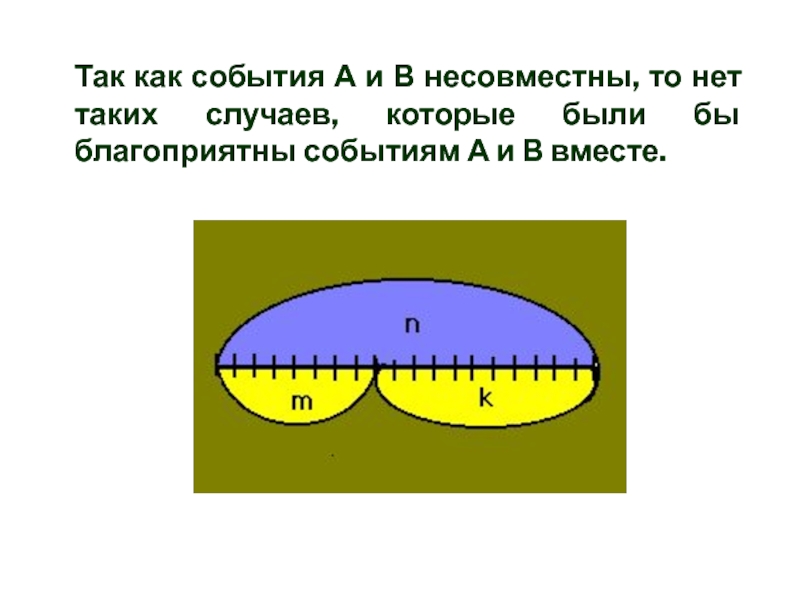
Слайд 20Так как события А и В несовместны, то нет таких
случаев, которые были бы благоприятны событиям А и В вместе.
Слайд 23
Если события А1, А2,…Аn образуют полную группу несовместных событий, то
их суммарная вероятность равна 1.
Следствие 1.
Слайд 24Так как события А1, А2,…Аn образуют полную группу, то появление
в опыте хотя бы одного из них будет достоверным событием.
Поэтому Р(А1+А2+…+Аn)=1. Так как эти события несовместны, то к ним применима теорема о сложении вероятностей:Доказательство:
Слайд 26Если события А и В совместны, то теорема о сложении
вероятностей обобщается следующим образом:
Р(А+В)=Р(А)+Р(В)-Р(АВ)
Отсюда можно выразить вероятность произведения событий А
и В:Р(АВ)= Р(А)+Р(В)- Р(А+В)
Слайд 28События А и В будут совместными. Поэтому по теореме о
сложении вероятностей вероятность того, что наугад выбранный сотрудник будет партийным
определится по формулеПусть событие А заключается в том, что случайно выбранный сотрудник принадлежит к партии любителей пива, а событие В - что сотрудник принадлежит к партии зеленых.
Решение.
Слайд 30Пример 2.
Молодой человек рассматривает три
возможности уклониться от службы в
армии.
Во-первых, он может поступить учиться в ВУЗ,
во-вторых, он
может быть освобожден от армии по состоянию здоровья, и в третьих,
он может жениться и к моменту призыва
обзавестись двумя детьми. Вероятности этих
событий для него равны, соответственно, 0.5,
0.2 и 0.01. Считая эти события несовместными,
найти вероятность того, что молодой
человек не попадет в ряды призывников
Слайд 31Решение.
Пусть событие А заключается в том, что молодой человек поступит
в ВУЗ, событие В - что он получит освобождение по
состоянию здоровья и событие С - что он женится и обзаведется двумя детьми.Т.к. эти события несовместны, то применяем теорему о сложении вероятностей в виде:
Р(А+В+С)=Р(А)+Р(В)+Р(С)
Слайд 33Теорема умножения вероятностей. Условная вероятность
Условной вероятностью
называется вероятность события В, вычисленная в предположении, что
событие А уже наступило.Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Два события называются независимыми, если появление любого из них не изменяет вероятность появления другого:
Вероятность совместного появления двух независимых событий равна произведению их вероятностей:
Слайд 34Теорема умножения вероятностей. Условная вероятность
Вероятность совместного наступления конечного числа событий
равна произведению вероятности одного из них на условные вероятности всех
остальных, причем условная вероятность каждого последующего события вычисляется в предположении, что все предыдущие уже наступили:Р(А1А2А3…Аn)=Р(А1)РА1(А2)РА1А2(А3)…РА1А2А3 …Аn-1(Аn);
РА1А2А3…Аn-1(Аn) – вероятность появления события Аn , вычисленная в предположении, что события А1А2А3…Аn-1 произошли
Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:
Вероятность появления хотя бы одного из событий А1А2А3…Аn , независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
Слайд 35
Формула полной вероятности является следствием теорем о сложении и умножении
вероятностей.
Пусть требуется определить вероятность события А, которое может произойти
только вместе с одним из событий Н1,Н2…Нn образующих полную группу несовместных событий. ФОРМУЛА ПОЛНОЙ
ВЕРОЯТНОСТИ
Эти события называются гипотезами.
Слайд 36По теореме об умножении вероятностей
Отсюда вытекает формула полной вероятности:
Так как
гипотезы Н1,Н2…Нn несовместны, то и комбинации Н1А, Н2А … НnА
тоже несовместны. Тогда по теореме о сложении вероятностейТак как гипотезы образуют полную группу, то событие А может появиться только в комбинации с одной из этих гипотез. Поэтому,
Слайд 37Формула полной вероятности.
Вероятность события А, которое может наступить только
при условии появления одного из событий H1, H2, H3,…,Hn ,
образующих полную группу попарно несовместных событий, равна сумме произведений вероятностей каждого из событий H1, H2, H3,…,Hn на соответствующую условную вероятность события А :Формула полной вероятности
Слайд 39
Студент, выйдя из дома за 30 минут до
начала занятий,
может приехать
в институт автобусом, троллейбусом или
трамваем. Все эти
варианты равновозможны.Вероятность приехать на занятия вовремя
для этих видов транспорта соответственно
равна 0.99, 0.98 и 0.9. Какова вероятность,
что студент приедет на учебу вовремя?
ПРИМЕР.
Слайд 40
Н1- студент поехал автобусом;
Н2- студент поехал троллейбусом;
Н3- студент поехал трамваем.
Чтобы
использовать формулу полной вероятности, необходимо знать вероятности каждой из гипотез
и условные вероятности события А для каждой из гипотез.Пусть событие А заключается в том, что студент не опоздает на занятия. Оно может произойти только вместе с одной из гипотез:
Решение:
Слайд 41
Так как гипотезы образуют полную группу событий, то суммарная вероятность
всех гипотез равна 1.
По условию задачи все гипотезы равновероятны,
следовательно Р(Н1)=Р(Н2)=Р(Н3)=1/3.
Условные вероятности события А для каждой из гипотез даны по условию задачи:
Р(А|Н1)=0.99; Р(А|Н2)=0.98; Р(А|Н3)=0.9
Следовательно, по формуле полной вероятности,
Слайд 43Формула полной вероятности.
Рассмотрим события В1, В2, В3,…,Вn которые образуют
полную группу событий и при наступлении каждого из них Вi
событие А может наступать с некоторой условной вероятностьюТогда вероятность наступления события А равна сумме произведений вероятностей каждого из событий на соответствующую условную вероятность события А
Сколько бы не было вероятностей:
Слайд 44ТЕОРЕМА ГИПОТЕЗ
(ФОРМУЛА БАЙЕСА)
Пусть имеется полная группа несовместных гипотез Н1,Н2…Нn .
Вероятности этих гипотез до опыта считаются известными: Р(Н1),Р(Н2)…Р(Нn).
Производится опыт,
в результате которого происходит событие А. Как следует изменить вероятности гипотез в связи с появлением события А?
Слайд 45Определим условные вероятности каждой из гипотез Р(Нi/А).
По теореме об умножении
вероятностей:
Отсюда
По формуле полной вероятности
Слайд 47Формула Байеса
Рассмотрим событие А которое может наступить при условии появления
одного из несовместных событий, В1, В2, В3,…,Вn , которые образуют
полную группу событий. Если событие А уже произошло то вероятность событий может быть переоценена по формуле Байеса, формуле вероятности гипотез:Слайд 48Перед экзаменом студент с равной
вероятностью может спрятать шпаргалку
в
одно из трех мест: в ботинок, в карман и
в
рукав. Вероятность вытащить на экзамене шпаргалку незаметно для преподавателя
в первом случае составляет 0.4, во втором
– 0.6, в третьем – 0.55. Студент, придя
на экзамен, благополучно достал шпаргалку
и списал ответ. Какова вероятность,
что он достал шпаргалку из ботинка?
ПРИМЕР 1.
Слайд 49Н1- достал шпаргалку из ботинка;
Н2- достал шпаргалку из кармана;
Н3- достал
шпаргалку из рукава.
Событие А в этой задаче заключается в том,
что студент благополучно достал шпаргалку. Это событие произошло в результате опыта.Оно могло осуществиться только вместе с одной из гипотез:
Решение:
Слайд 50Т.е. требуется определить условную вероятность первой гипотезы, при условии, что
событие А имело место.
Для этого используем формулу Байеса.
По условию
задачи все гипотезы равновероятны, следовательно Р(Н1)=Р(Н2)=Р(Н3)=1/3.
В данной задаче требуется определить вероятность того, что студент достал шпаргалку из ботинка, если известно, что он незаметно списал.
Слайд 51Тогда
Условные вероятности события А для каждой из гипотез даны по
условию задачи:
Р(А|Н1)=0.4; Р(А|Н2)=0.6; Р(А|Н3)=0.55
Слайд 52ПРИМЕР 2.
Статистика запросов кредитов в банке:
10 % - государственные
органы,
30 % - банки, 60 % - физические лица.
Вероятности не возврата кредита для них соответственно равны 0.01, 0.05, 0.2.
Найти вероятность события А – не возврата
очередного кредита и
вероятность события В - что кредит не
возвратил некоторый банк, если известно,
что событие А произошло.
Слайд 53Гипотезами в этой задаче будут:
Н1- кредит взял государственный орган;
Н2- кредит
взял банк;
Н3- кредит взяло физическое лицо.
Вероятность события А найдем по
формуле полной вероятности. Решение:
Найдем вероятности гипотез:
Р(Н1)=0.1; Р(Н2)=0.3; Р(Н3)=0.6
Слайд 54Условные вероятности события А для каждой из гипотез даны в
задаче:
Р(А|Н1)=0.01; Р(А|Н2)=0.05; Р(А|Н3)=0.2.
Тогда:
Вероятность события В - это условная вероятность
гипотезы Н2 : Р(Н2/А). Находим ее по формуле Бейеса:
Слайд 55Формула Бернулли
Вероятность того что в n независимых испытаниях в каждом
из которых вероятность появления события равна Р , Р(0
событие наступит К раз безразлично в какой последовательности, вычисляется по формуле Бернуллиq=1-p ; q- вероятность противоположного события
или
Слайд 56
Если производится n независимых опытов, в
каждом из которых событие
А появляется с
вероятностью Р, то вероятность того, что
событие А
произойдет m раз выражается какФормула Бернулли
Слайд 57
Известно, если монета упадет орлом, студент
идет пить пиво, если
монета упадет решкой
– студент идет на свидание с девушкой,
если монета встанет на ребро, он пойдет
в библиотеку, а если повиснет в воздухе –
студент отправится на лекции. Если бы
все эти исходы опыта были равновозможными,
то какова была бы вероятность, что при пяти
бросаниях монеты 1) трижды выпала
необходимость идти на лекцию и
2) хотя бы один раз выпала такая необходимость?
ПРИМЕР.
Слайд 58
Решение:
Тогда вероятность противоположного события
составит q=3/4.
По формуле Бернулли находим вероятность
того, что при 5 бросаниях монеты трижды случится это событие:
1)
В данной задаче проводится серия из 5 независимых опытов, причем вероятность того, что монета повиснет в воздухе в каждом опыте составляет р= 1/4. Слайд 59
Чтобы найти вероятность того, что при 5 бросаниях хотя бы
один раз монета повиснет в воздухе, перейдем к вероятности противоположного
события - монета ни разу не повиснет в воздухе: Р0,5 .Тогда искомая вероятность будет: Р=1- Р0,5
Вероятность Р0,5 опять найдем по формуле Бернулли:
Слайд 61Асимптотические формулы
Если число испытаний велико, то использование формулы Бернулли будет
нецелесообразным в силу необходимости выполнения громоздких вычислений. Теорема Муавра-Лапласа, дающая
асимптотическую формулу , позволяет вычислить вероятность приближенно.Теорема: Если вероятность наступления события А в каждом из n независимых испытаниях равна p и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность Рn(m) того, что в n испытаниях событие А наступит m раз, приближенно равна значению функции