лекции:
Поиск в глубину в ориентированных графах (напомнить!)
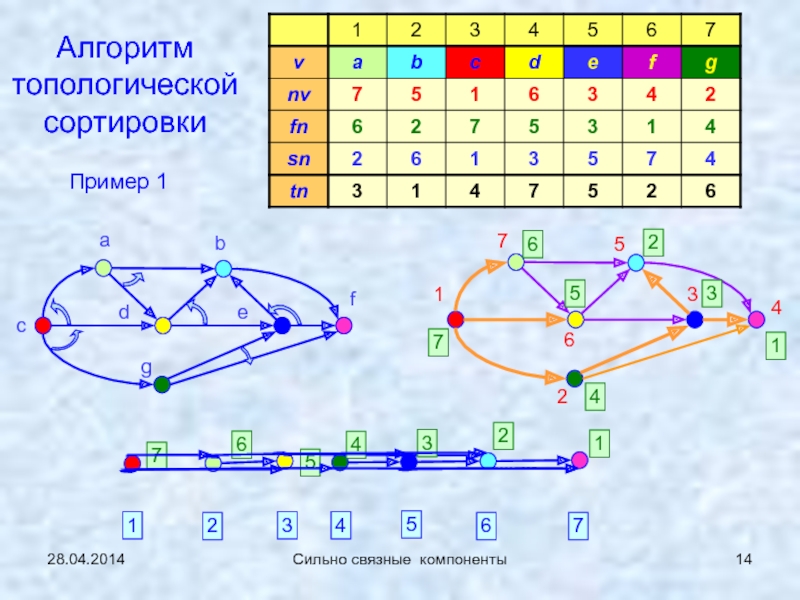
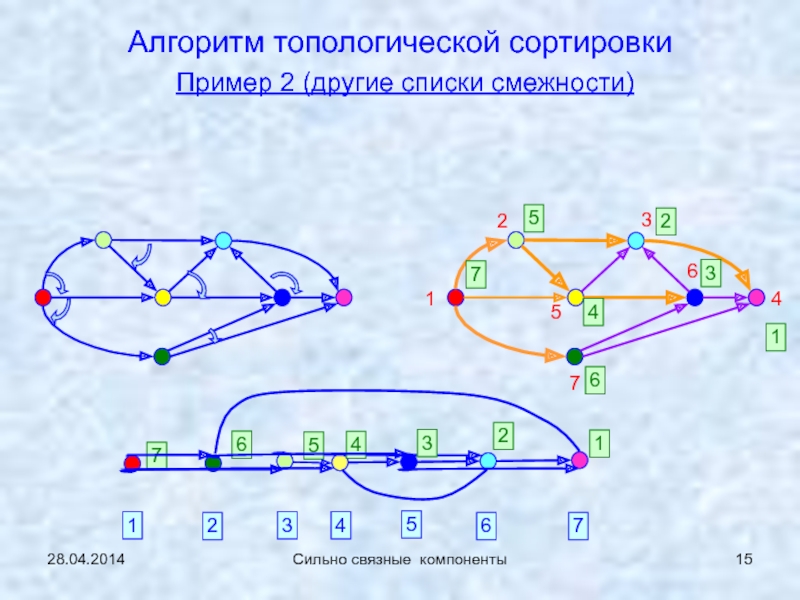
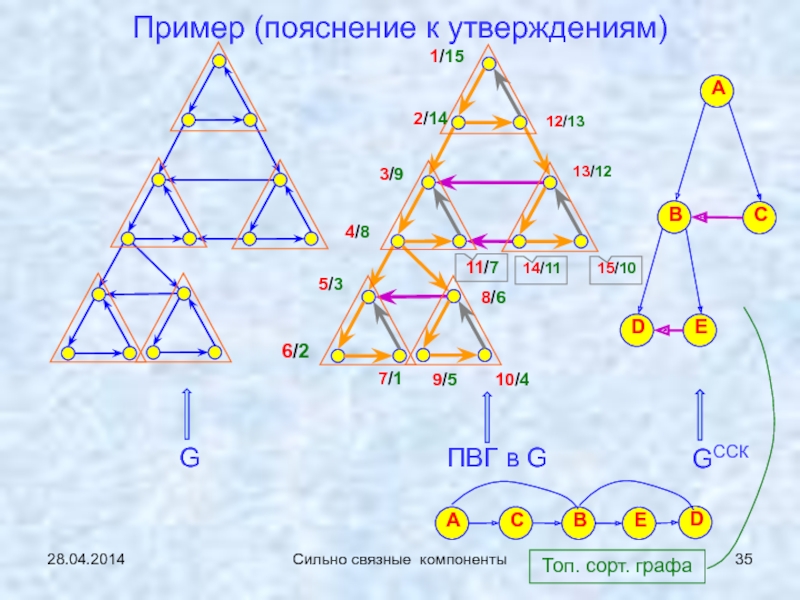
Топологическая сортировка
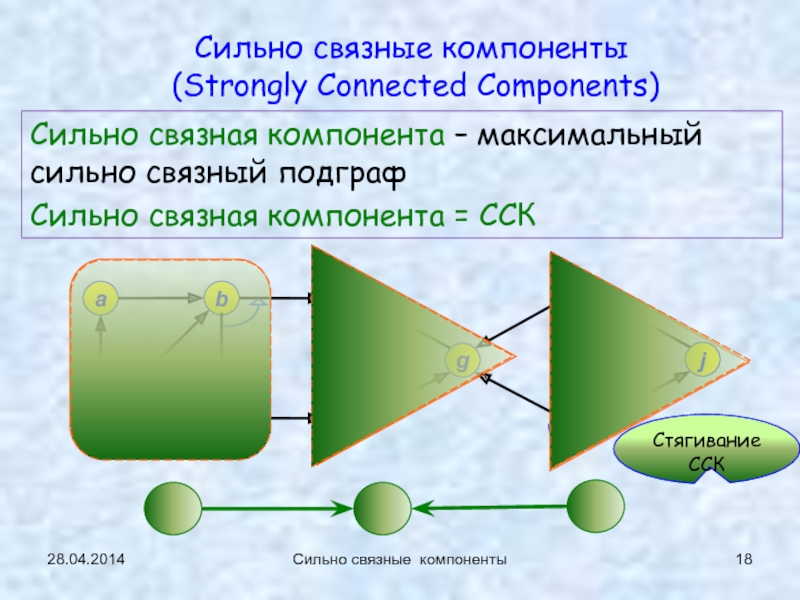
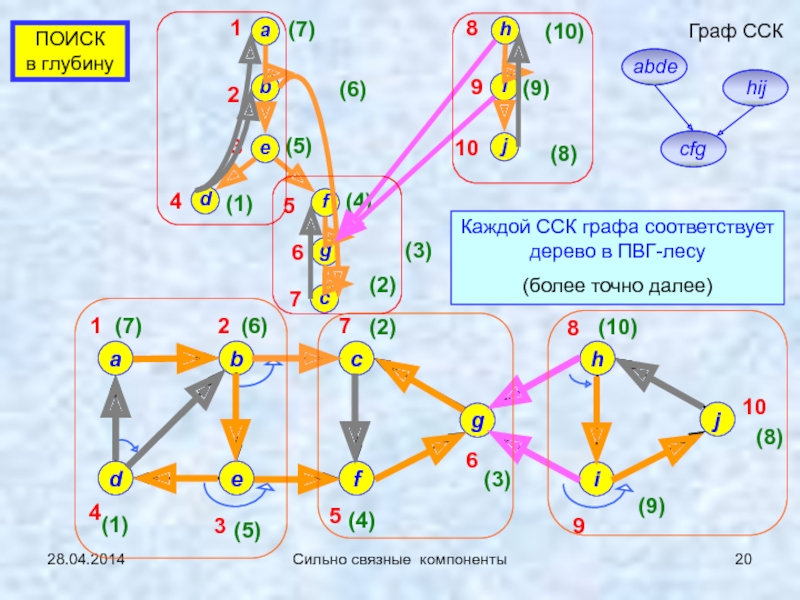
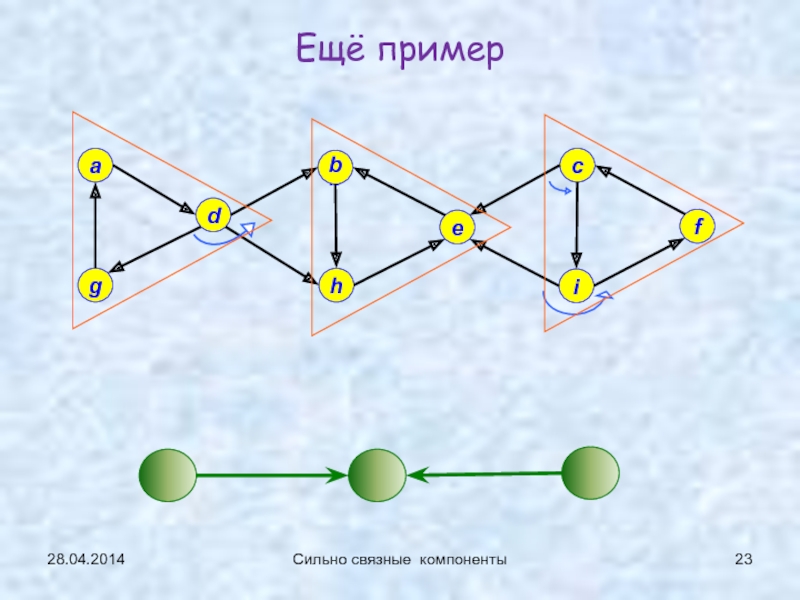
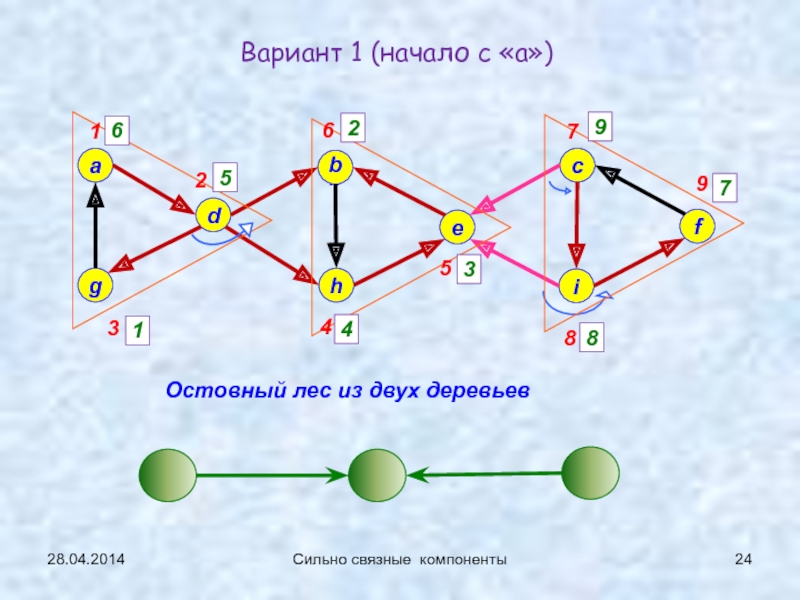
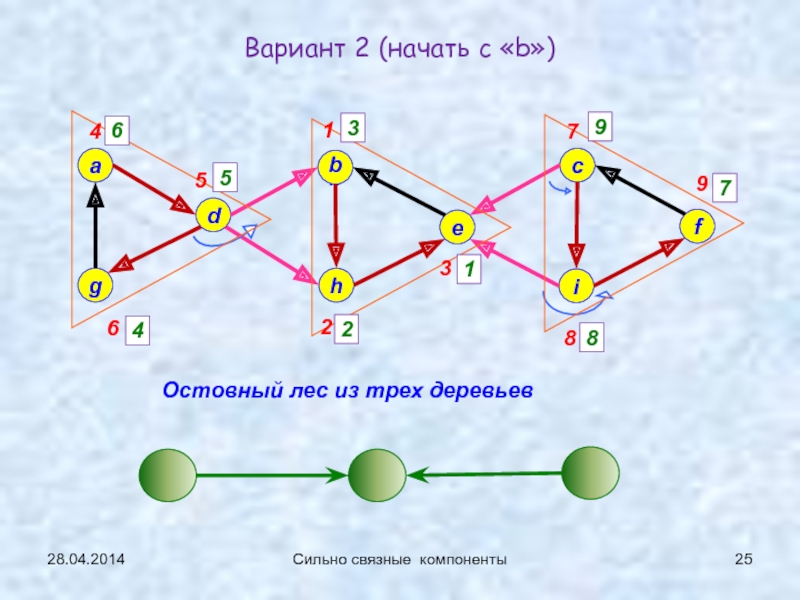
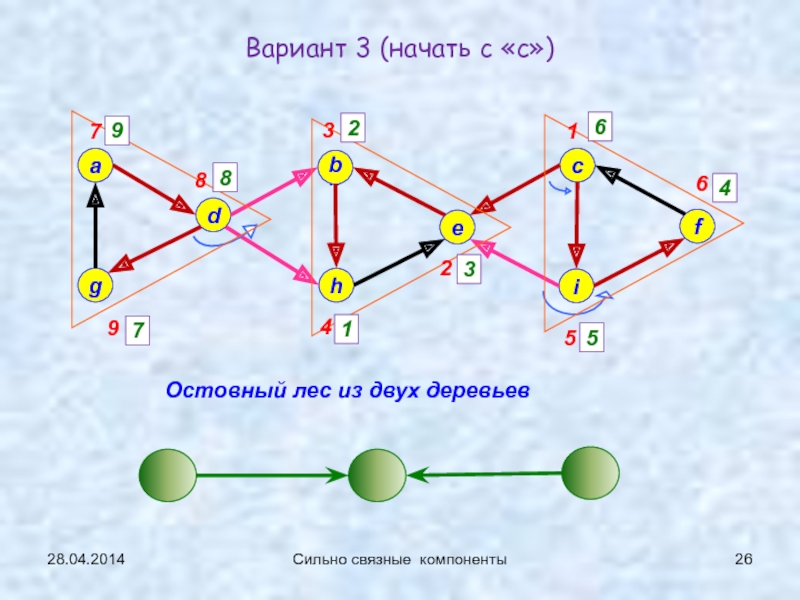
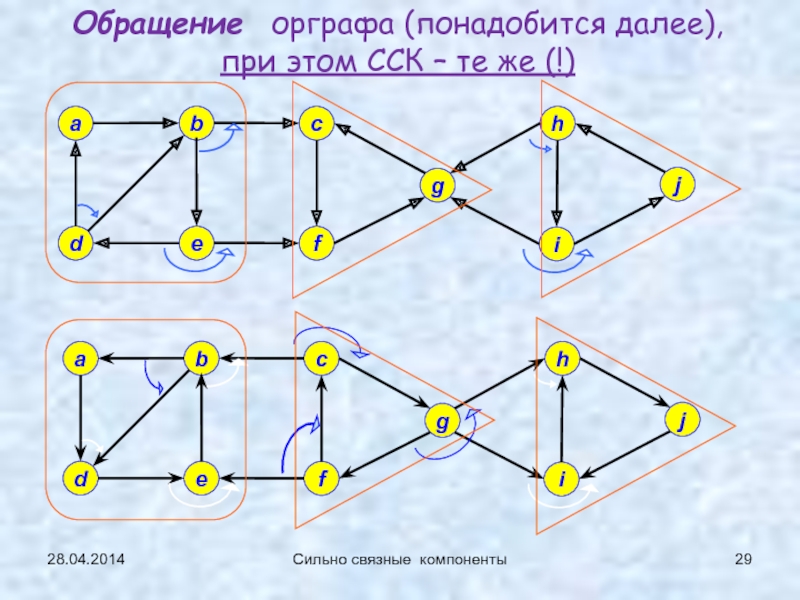
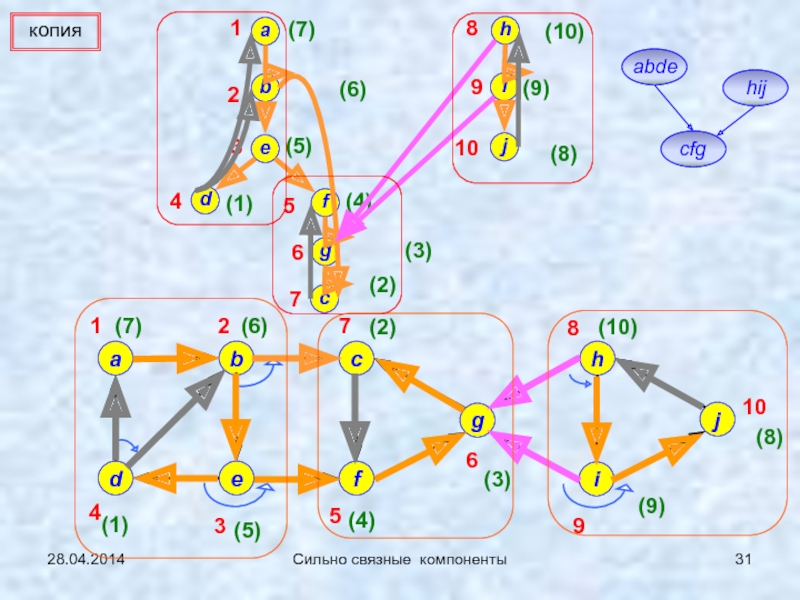
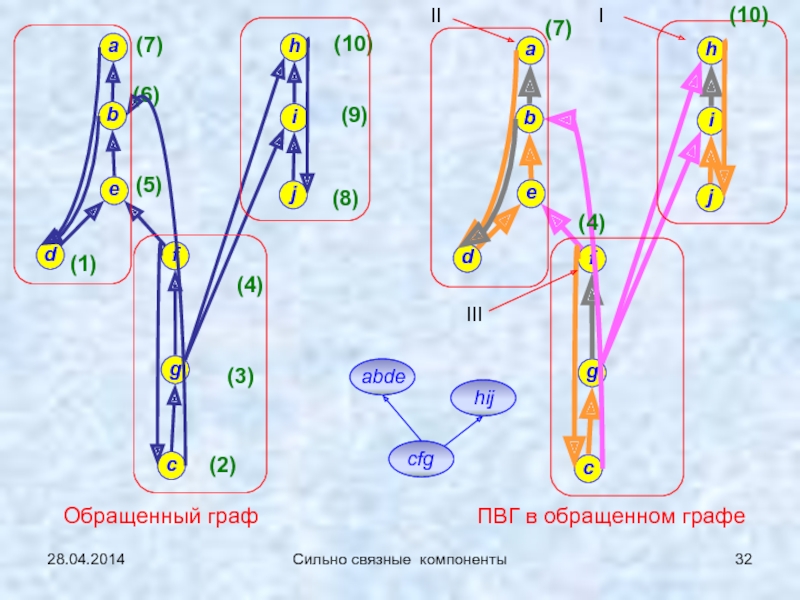
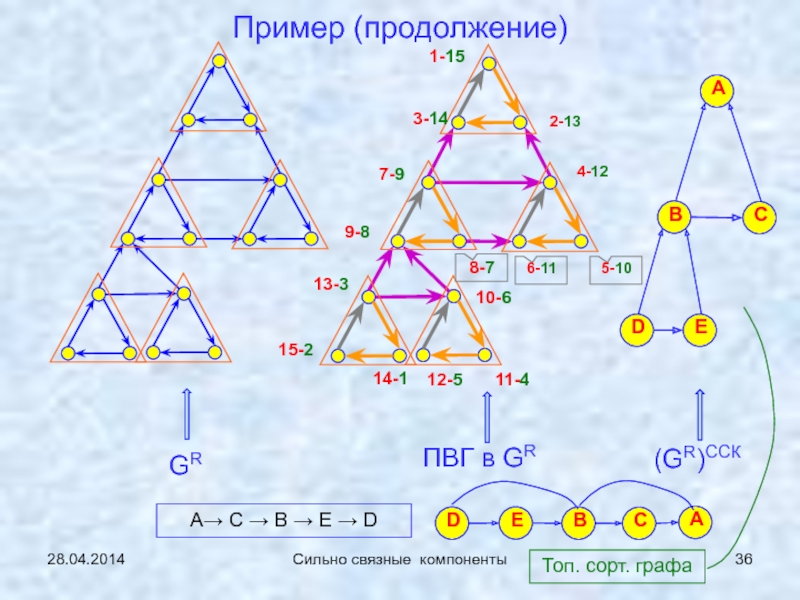
Сильно связные
компоненты (сл.17…)1-2: 21.04.2014
3: 28.04.14


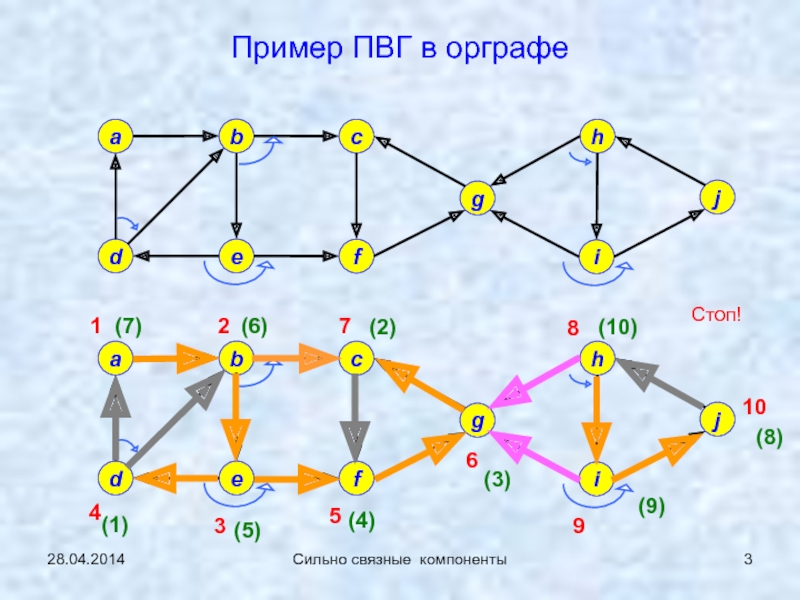
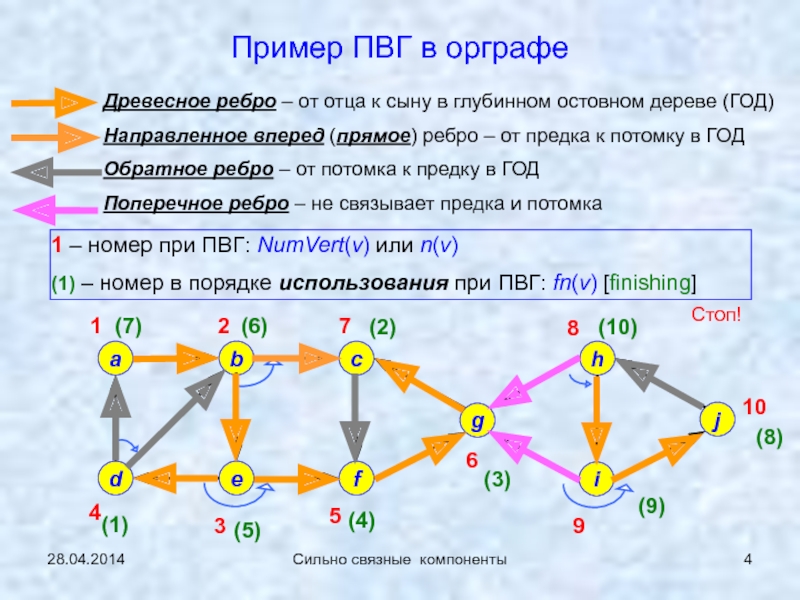
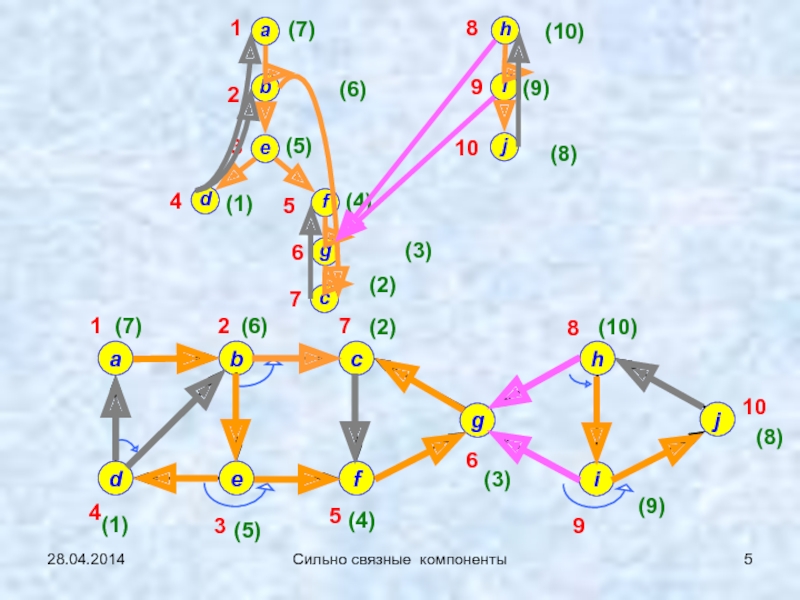
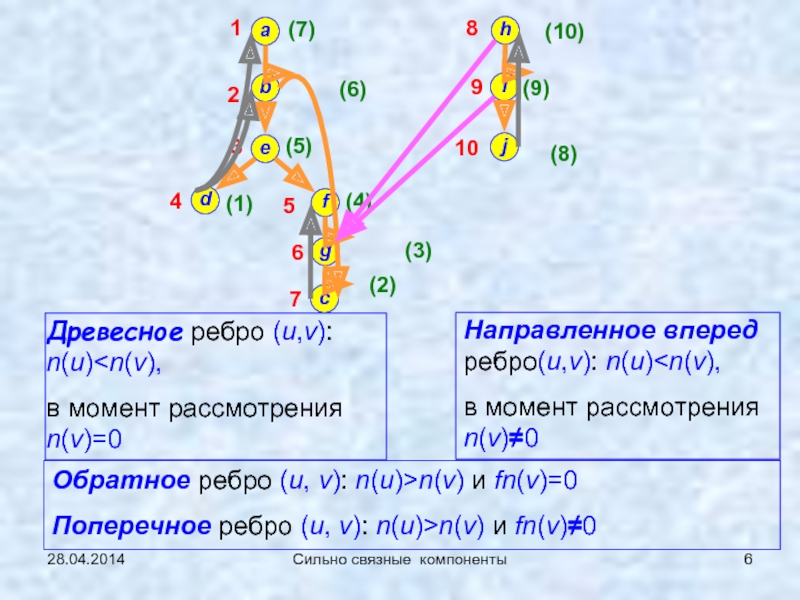

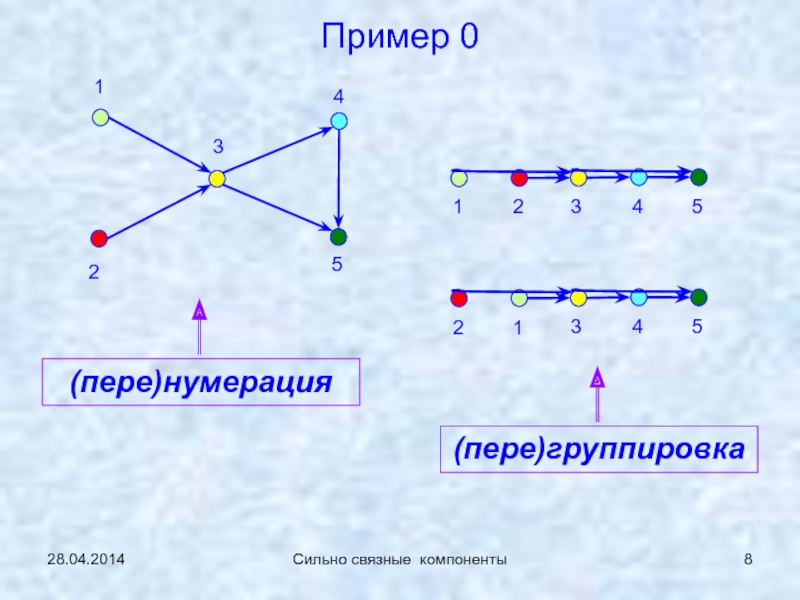
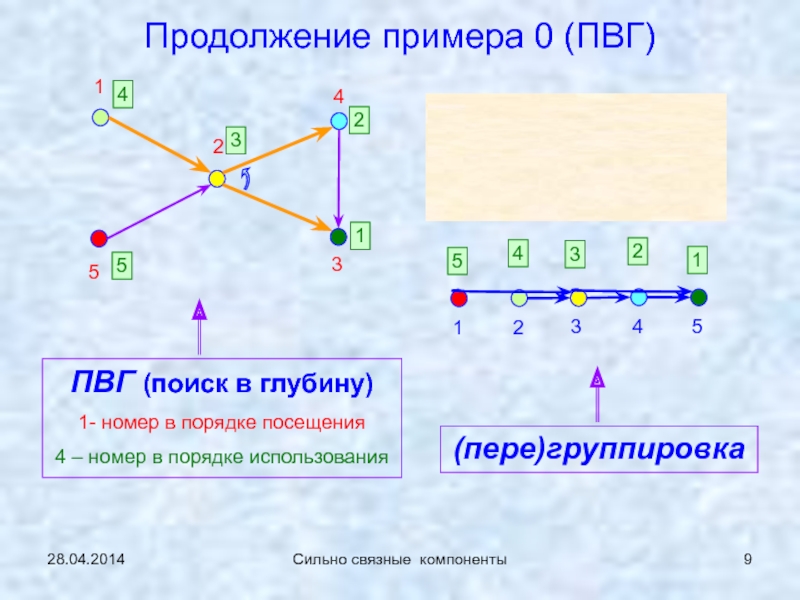
![Особенности поиска в глубину (ПВГ) в ориентированных графах 28.04.2014Сильно связные компонентыПродолжение примера 0 (ПВГ)v [*] – имена вершин в 28.04.2014Сильно связные компонентыПродолжение примера 0 (ПВГ)v [*] – имена вершин в исходной нумерации; nv [*] - номера](/img/thumbs/defdfc6f2df3e4cb1aff9d1f2deeebe8-800x.jpg)
![Особенности поиска в глубину (ПВГ) в ориентированных графах 28.04.2014Сильно связные компонентыПродолжение примера 0 (ПВГ)1) Получение sn [*] из fn 28.04.2014Сильно связные компонентыПродолжение примера 0 (ПВГ)1) Получение sn [*] из fn [*]: for i := 1..n do](/img/tmb/2/153235/e67bf5f43419e562887fff1870b8db94-800x.jpg)
![Особенности поиска в глубину (ПВГ) в ориентированных графах 28.04.2014Сильно связные компонентыПерестановкиtn [sn [ i ]] := i , где 28.04.2014Сильно связные компонентыПерестановкиtn [sn [ i ]] := i , где i – из исходной нумерации, sn](/img/tmb/2/153235/a58eb7363ccefa02bd6dd47e6f6d5c7c-800x.jpg)
![Особенности поиска в глубину (ПВГ) в ориентированных графах 28.04.2014Сильно связные компонентыВыполнить ПВГ в орграфе G, заполнив массив fn[*].Пронумеровать вершины 28.04.2014Сильно связные компонентыВыполнить ПВГ в орграфе G, заполнив массив fn[*].Пронумеровать вершины номерами (n - fn[v] + 1),](/img/thumbs/d52d24f8a6b5caa56a6c569c1a096315-800x.jpg)