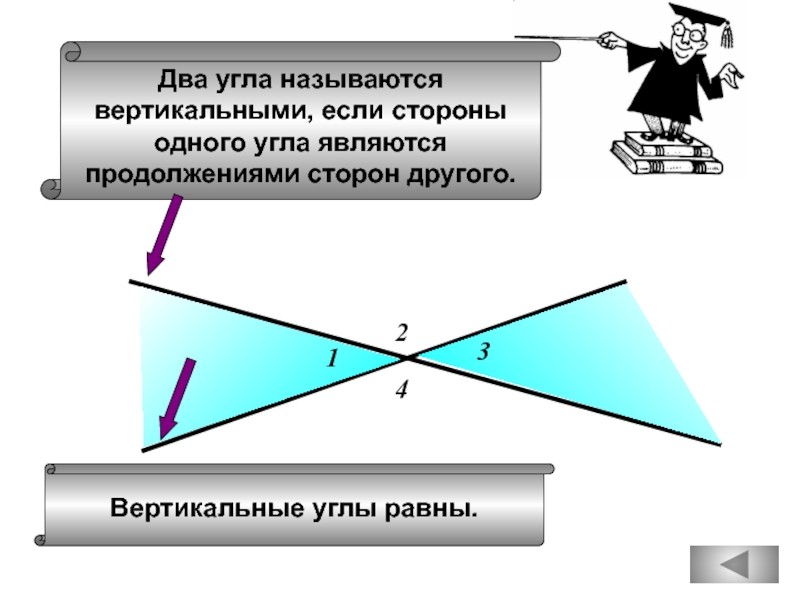
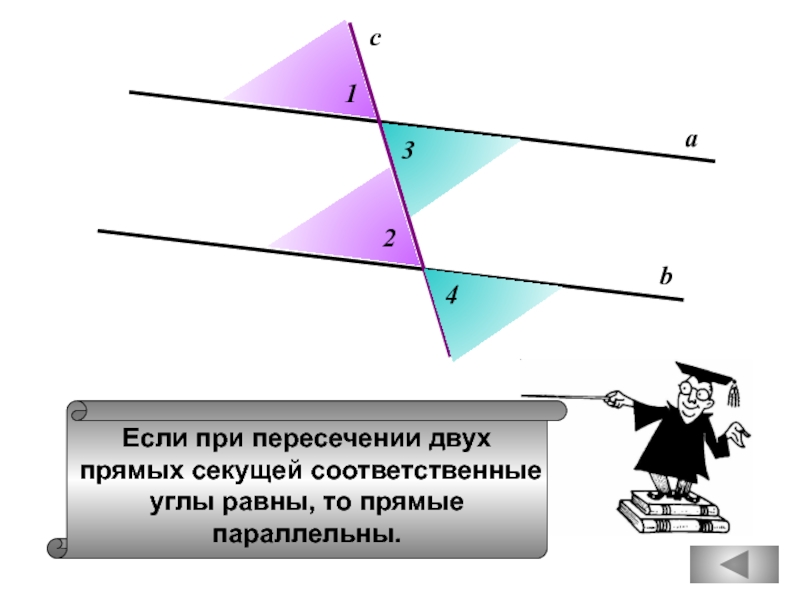
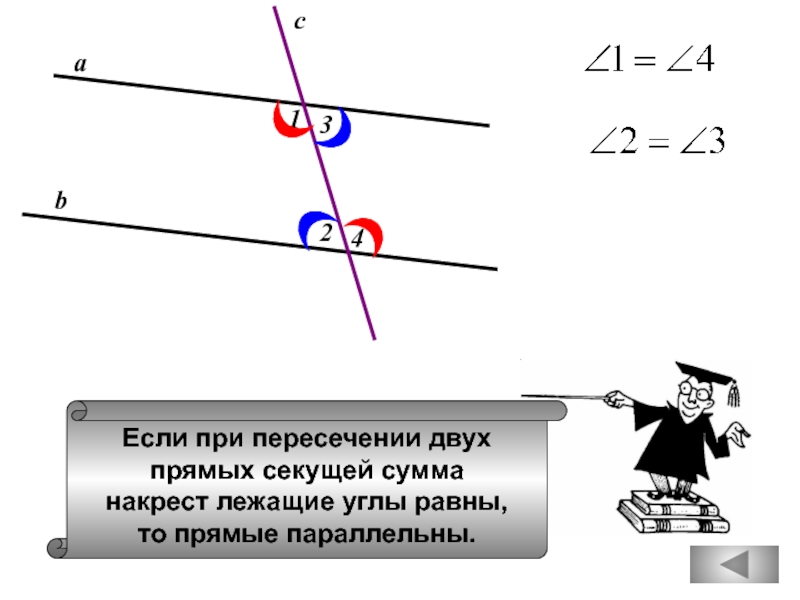
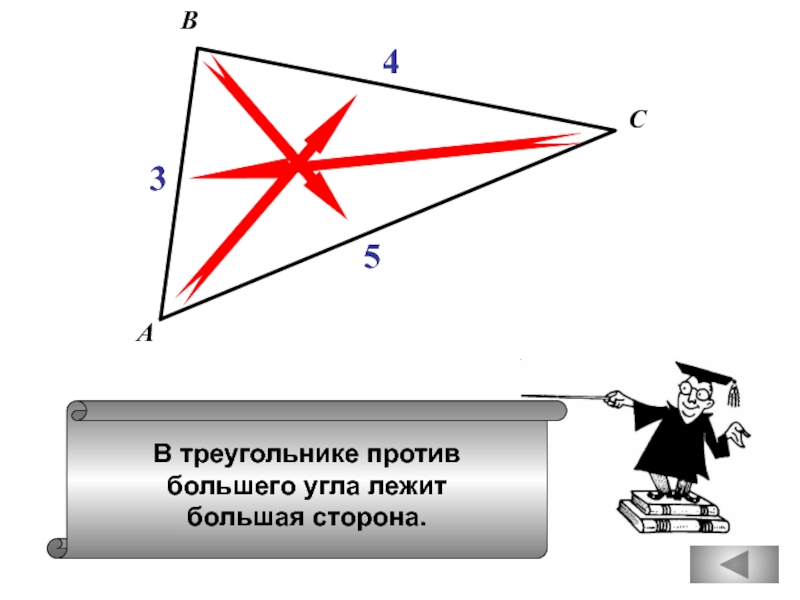
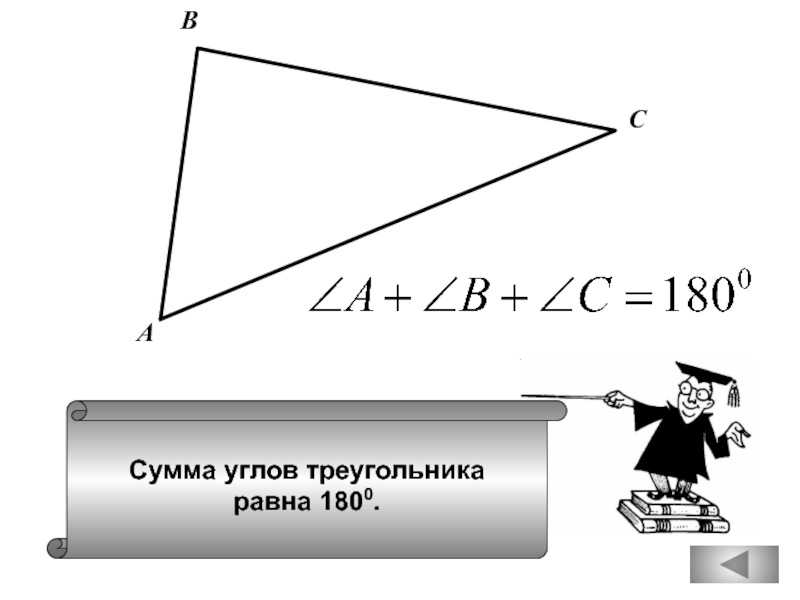
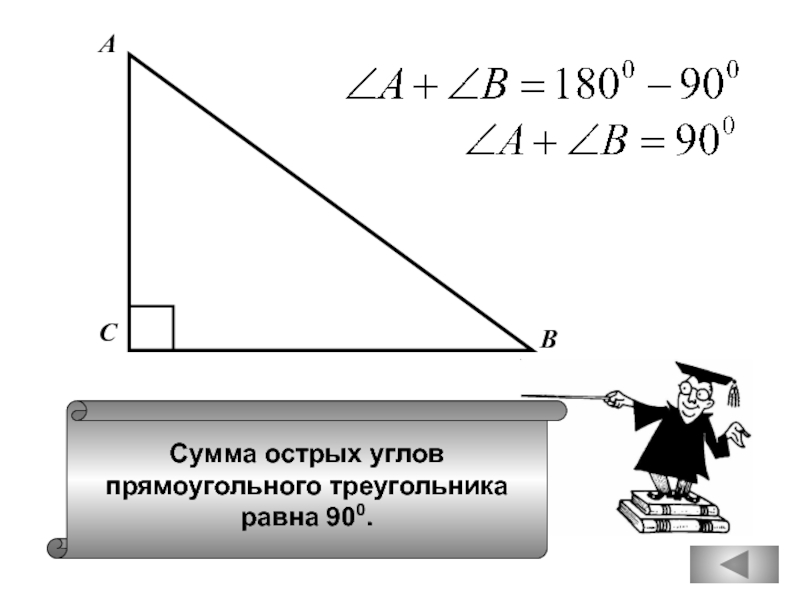
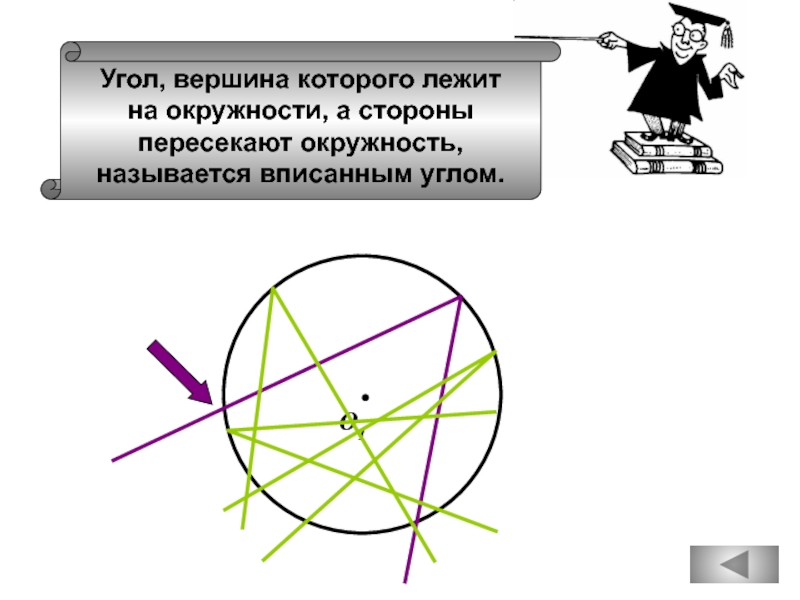
вертикальный с ним угол равен 450.
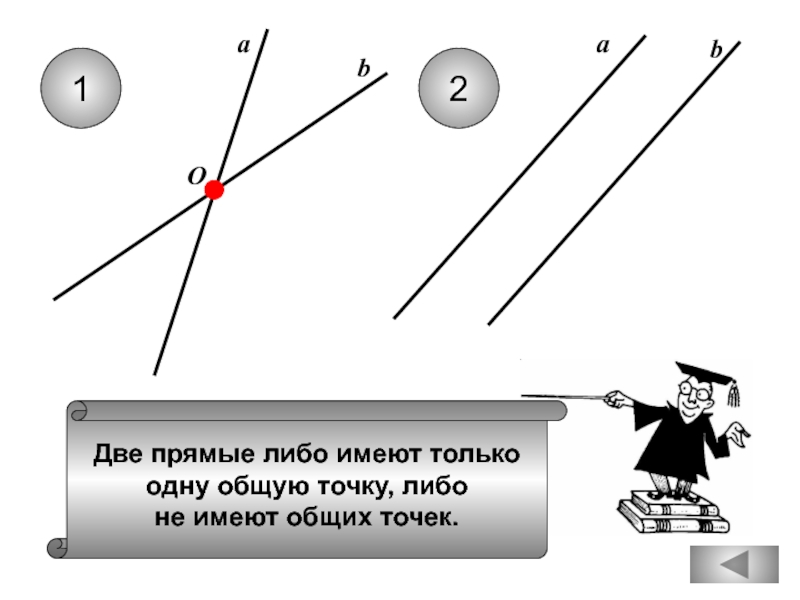
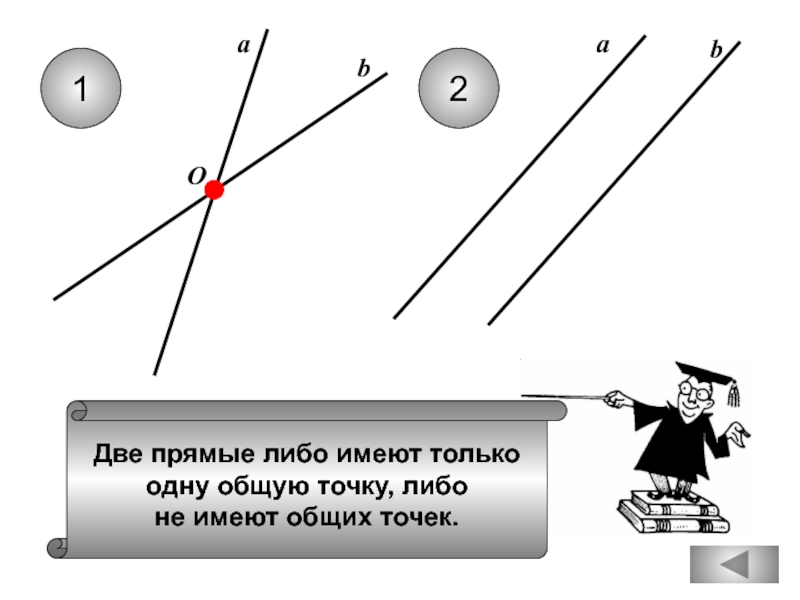
Любые две прямые имеют
ровно одну общую точку.
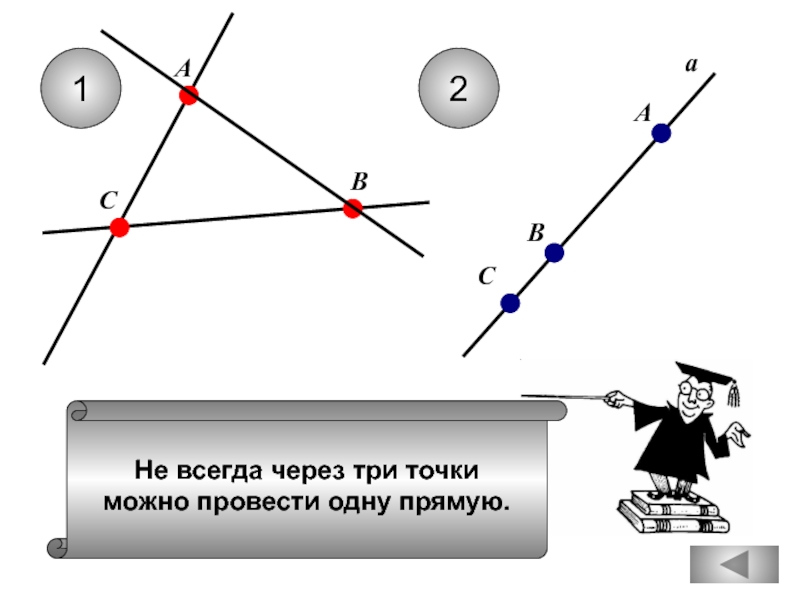
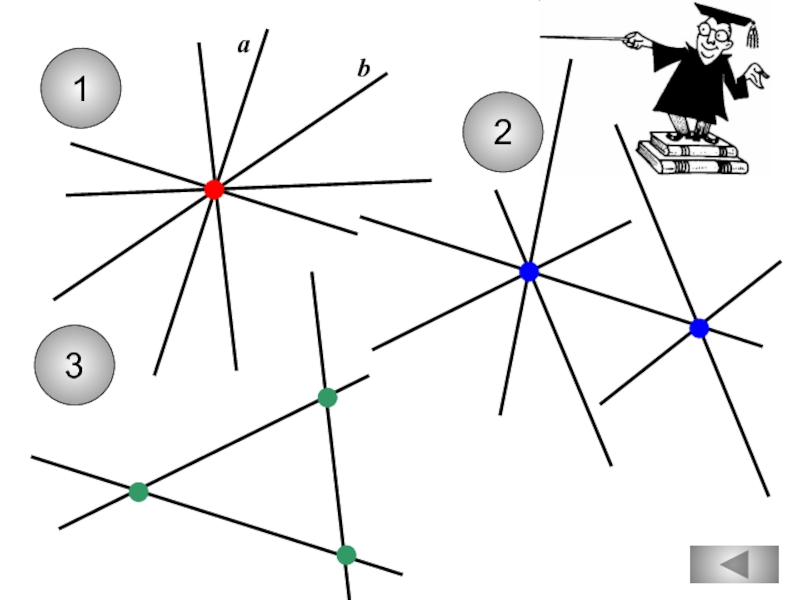
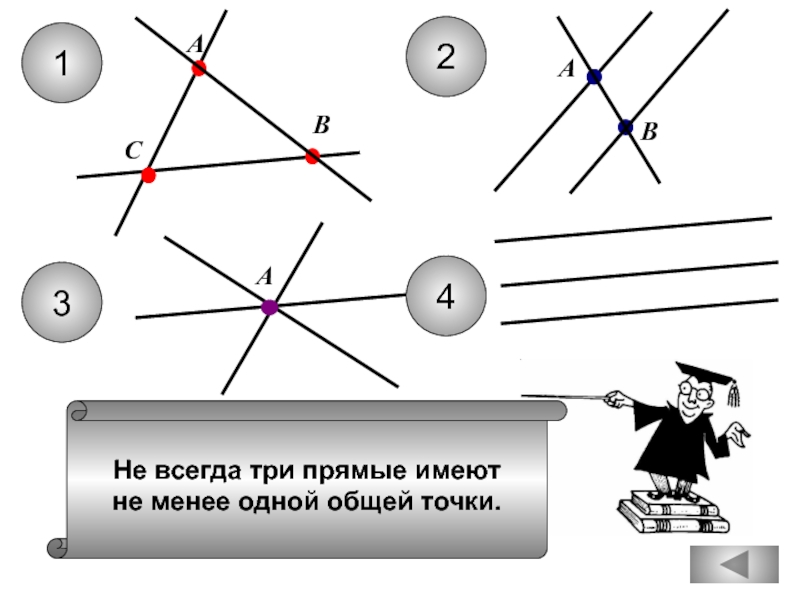
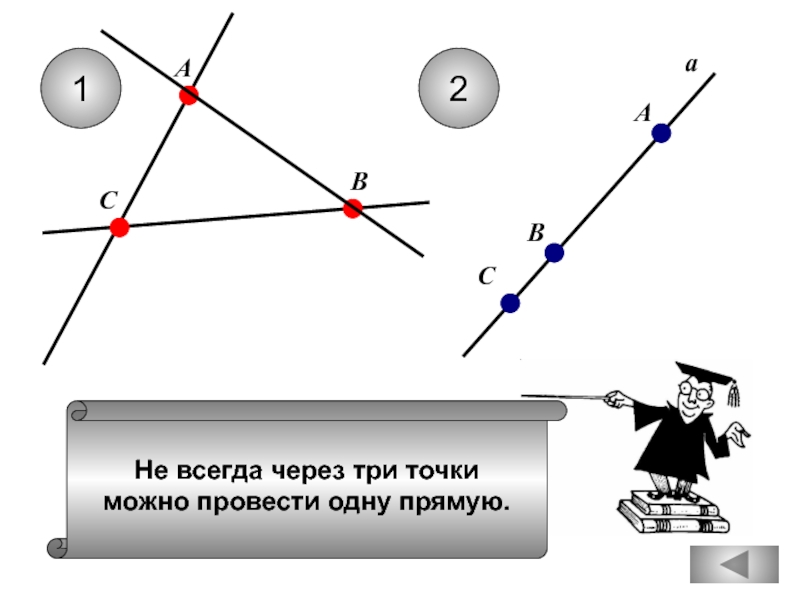
Через любые три точки проходит ровно
одна прямая.
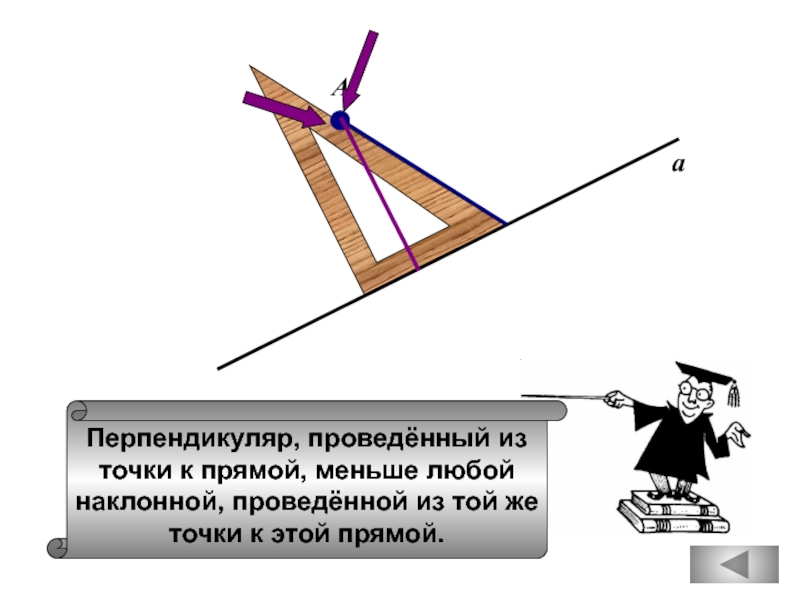
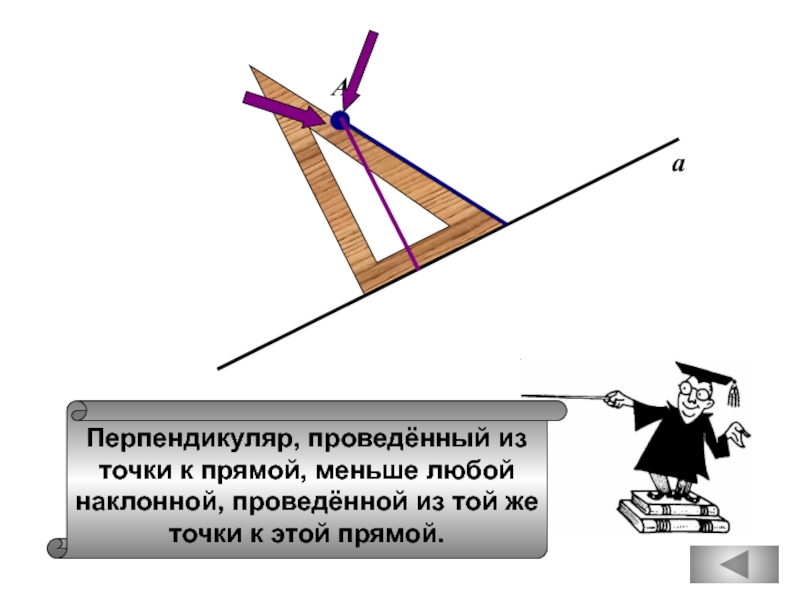
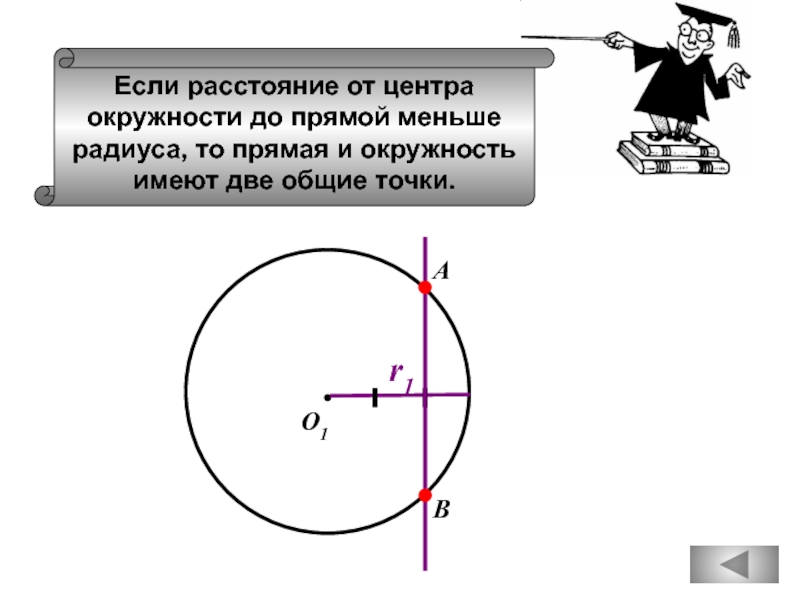
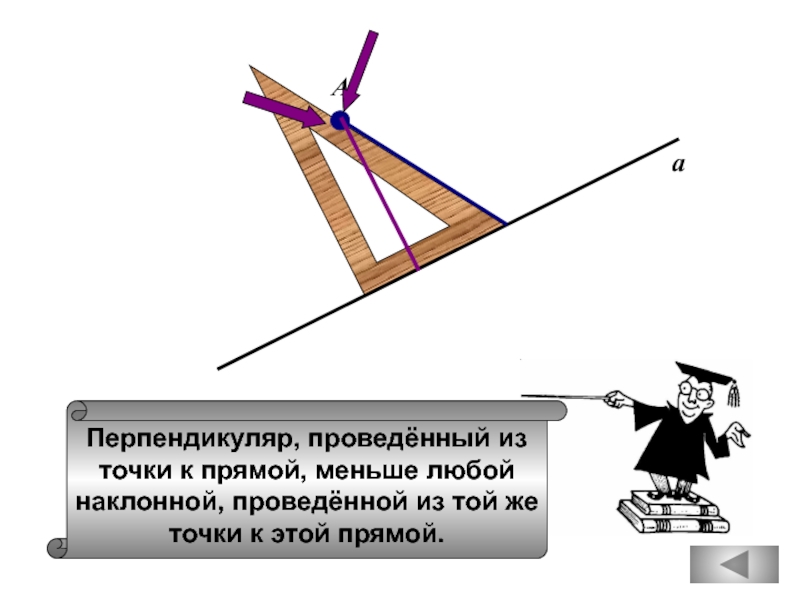
Если расстояние от точки до прямой меньше 1,
то и длина любой наклонной, проведенной
из данной точки к прямой, меньше 1.
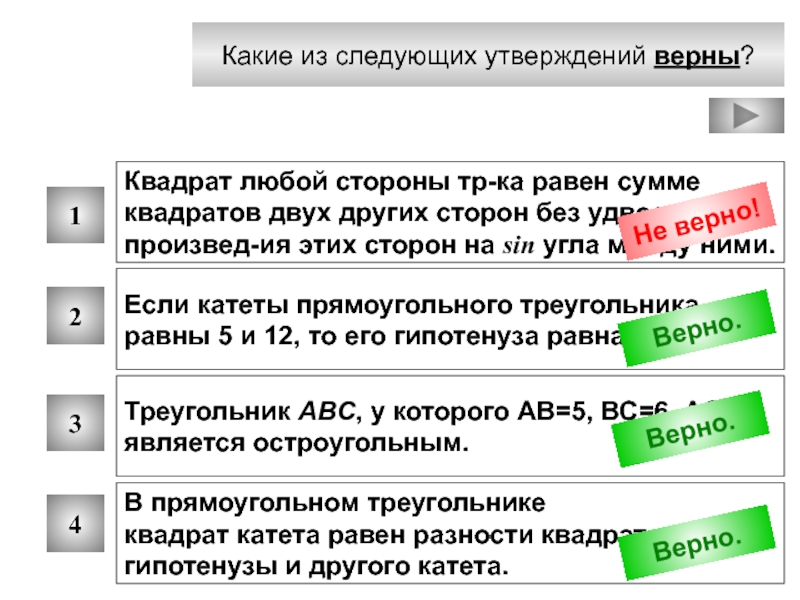
Верно.
Не верно!
Не верно!
Не верно!