Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ. ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ
Содержание
- 1. ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ. ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ
- 2. Задачи изучаемые начертательной геометрией можно разделить на позиционные, метрические и конструктивные
- 3. Позиционные задачи - задачи на относительное
- 4. Метрические задачи - задачи на определение расстояний и натуральных величин геометрических объектов.
- 5. Конструктивные задачи – задачи на построение геометрических фигур, отвечающих заданным условиям.
- 6. ПАРАЛЛЕЛЬНЫЕ ПРЯМАЯ И ПЛОСКОСТЬПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ
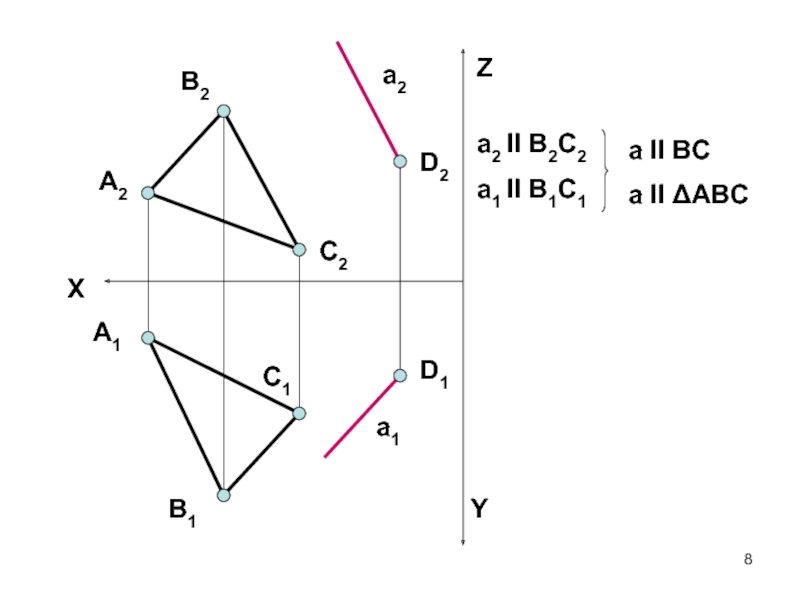
- 7. ПРЯМАЯ ПАРАЛЛЕЛЬНА ПЛОСКОСТИ, ЕСЛИ ОНА ПАРАЛЛЕЛЬНА ЛЮБОЙ ПРЯМОЙ ПРИНАДЛЕЖАЩЕЙ ЭТОЙ ПЛОСКОСТИПАРАЛЛЕЛЬНЫЕ ПРЯМАЯ И ПЛОСКОСТЬ
- 8. XYZA2B2A1C2C1B1a1a2D2D1a2 II B2C2a1 II B1C1a II BCa II ΔABC
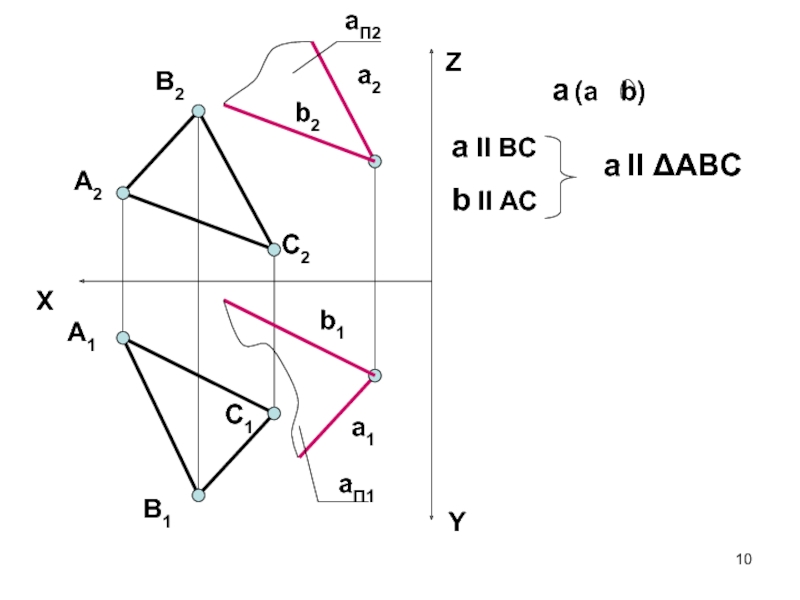
- 9. ПЛОСКОСТИ ПАРАЛЛЕЛЬНЫ, ЕСЛИ ДВЕ ПЕРЕСЕКАЮЩИЕСЯ ПРЯМЫЕ
- 10. XYZA2B2A1C2C1B1a1a2b1b2a II BCb II ACaП2aП1a (a b) a II ΔABC
- 11. ПРЯМАЯ ПЕРПЕНДИКУЛЯРНАЯ ПЛОСКОСТИ, ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТИПРЯМАЯ ПЕРПЕНДИКУЛЯРНА
- 12. 1. Горизонталь и фронталь ΔАВС – две
- 13. ДВЕ ПЛОСКОСТИ ПЕРПЕНДИКУЛЯРНЫ, ЕСЛИ ОДНА ПЛОСКОСТЬ ПРОХОДИТ ЧЕРЕЗ ПЕРПЕНДИКУЛЯР К ДРУГОЙПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТИ
- 14. Зададим плоскость перпендикулярную ΔАВС двумя пересекающимися прямыми.Одна
- 15. ПЕРЕСЕКАЮЩИЕСЯ ПРЯМАЯ И ПЛОСКОСТЬ ПЕРЕСЕКАЮЩИЕСЯ ПЛОСКОСТИ
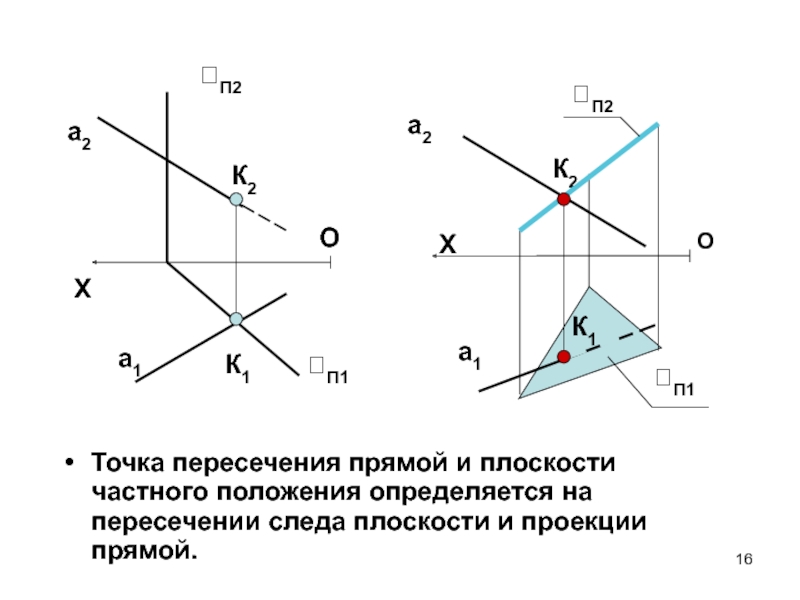
- 16. Точка пересечения прямой и плоскости частного положения определяется на пересечении следа плоскости и проекции прямой.XOa1а2П1П2К1К2XOa1а2П1П2К1К2
- 17. 1. ПЛОСКОСТИ ПЕРЕСЕКАЮТСЯ, ЕСЛИ У НИХ ЕСТЬ
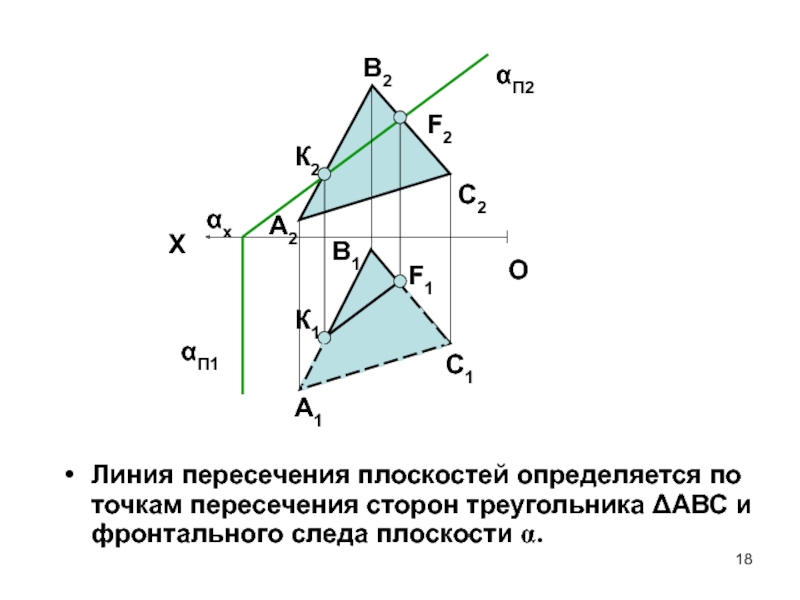
- 18. Линия пересечения плоскостей определяется по точкам пересечения сторон треугольника ΔАВС и фронтального следа плоскости α.XOК2F2F1К1A2B2C2B1A1C1αП1αП2αx
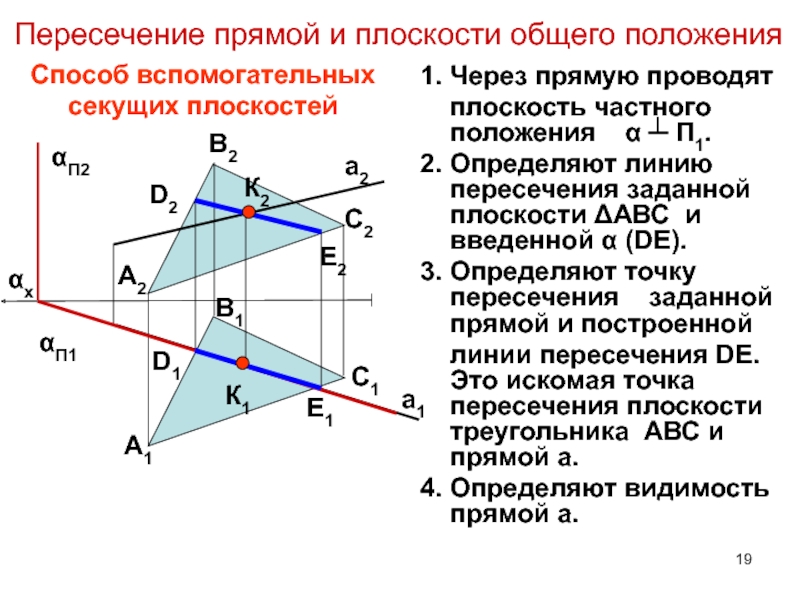
- 19. Пересечение прямой и плоскости общего положения1. Через
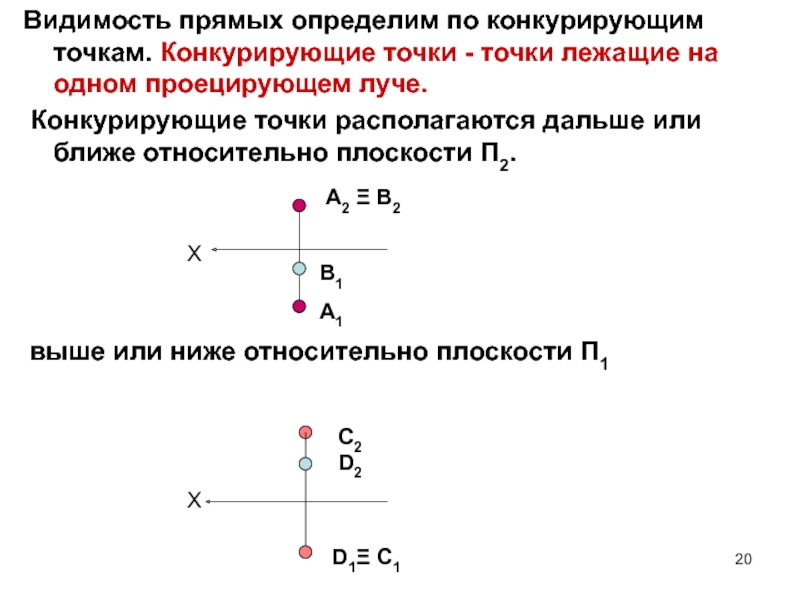
- 20. Видимость прямых определим по конкурирующим точкам. Конкурирующие
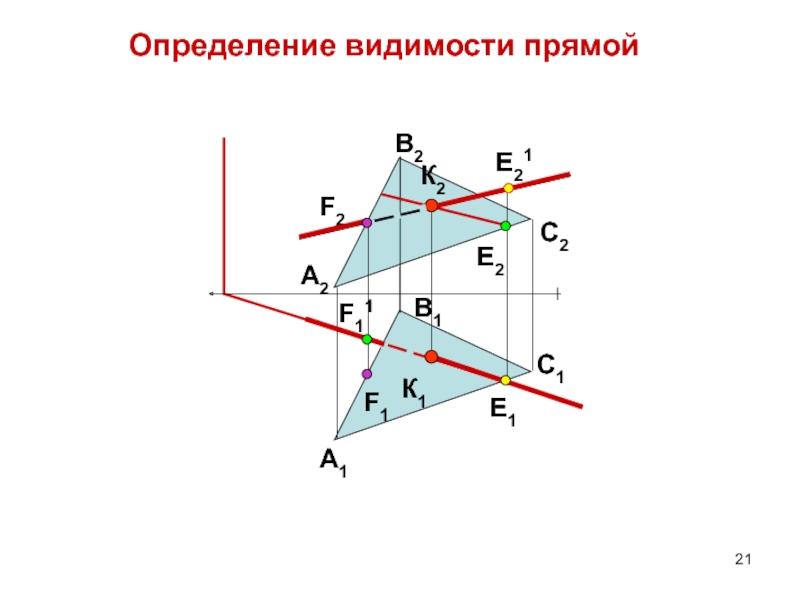
- 21. Определение видимости прямойЕ2F11E1F2Е21F1C1A2С2B2A1B1К1К2
- 22. Внешний контур всегда виден.Если внутри контура пересекаются
- 23. ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ ОБЩЕГО ПОЛОЖЕНИЯК1A2В2С2A1В1С1D2F2E2D1F1E1αп212221121bп23242x4131L1К2L1Построить линию пересечения треугольников
- 24. ОПРЕДЕЛЕНИЕ ВИДИМОСТИ СТОРОН ТРЕУГОЛЬНИКАК1A2В2С2A1В1С1D2F2E2D1F1E1αп212221121bп23242x4131L1К2L1 Видимость определяем по
- 25. Слайд 25
- 26. Слайд 26
- 27. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3 Позиционные задачи - задачи на относительное положение
геометрических объектов
Круг позиционных задач:
относительное положение
точек относительное положение прямых линий
относительное положение прямой и
плоскости
относительное положение плоскостей
относительное положение плоскости
и поверхности
относительное положение поверхностей
Слайд 4 Метрические задачи - задачи на определение расстояний и натуральных
величин геометрических объектов.
Слайд 5 Конструктивные задачи – задачи на построение геометрических фигур,
отвечающих заданным условиям.
Слайд 7 ПРЯМАЯ ПАРАЛЛЕЛЬНА ПЛОСКОСТИ, ЕСЛИ ОНА ПАРАЛЛЕЛЬНА ЛЮБОЙ ПРЯМОЙ
ПРИНАДЛЕЖАЩЕЙ ЭТОЙ ПЛОСКОСТИ
ПАРАЛЛЕЛЬНЫЕ ПРЯМАЯ И ПЛОСКОСТЬ
Слайд 9 ПЛОСКОСТИ ПАРАЛЛЕЛЬНЫ, ЕСЛИ ДВЕ ПЕРЕСЕКАЮЩИЕСЯ ПРЯМЫЕ ОДНОЙ ПЛОСКОСТИ, ПАРАЛЛЕЛЬНЫ ДВУМ
ПЕРЕСЕКАЮЩИМСЯ ПРЯМЫМ ДРУГОЙ ПЛОСКОСТИ
ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ
Слайд 11ПРЯМАЯ ПЕРПЕНДИКУЛЯРНАЯ ПЛОСКОСТИ,
ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТИ
ПРЯМАЯ ПЕРПЕНДИКУЛЯРНА ПЛОСКОСТИ, ЕСЛИ ОНА ПЕРПЕНДИКУЛЯРНА
ДВУМ ПЕРЕСЕКАЮЩИМСЯ ПРЯМЫМ ПРИНАДЛЕЖАЩИМ ЭТОЙ ПЛОСКОСТИ
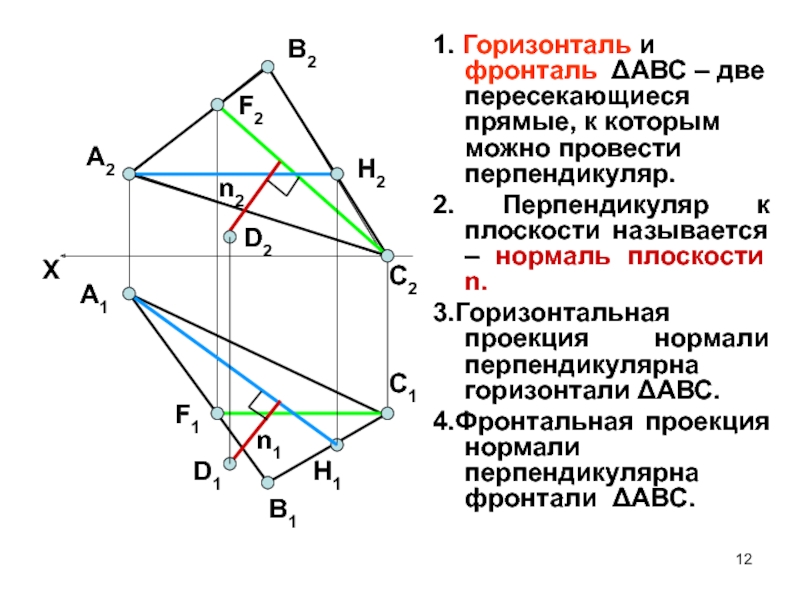
Слайд 121. Горизонталь и фронталь ΔАВС – две пересекающиеся прямые, к
которым можно провести перпендикуляр.
2. Перпендикуляр к плоскости называется – нормаль
плоскости n.3.Горизонтальная проекция нормали перпендикулярна горизонтали ΔАВС.
4.Фронтальная проекция нормали перпендикулярна фронтали ΔАВС.
А2
F2
В2
А1
F1
X
H2
H1
С1
С2
n2
n1
В1
D2
D1
Слайд 13ДВЕ ПЛОСКОСТИ ПЕРПЕНДИКУЛЯРНЫ, ЕСЛИ ОДНА ПЛОСКОСТЬ ПРОХОДИТ ЧЕРЕЗ ПЕРПЕНДИКУЛЯР К
ДРУГОЙ
ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТИ
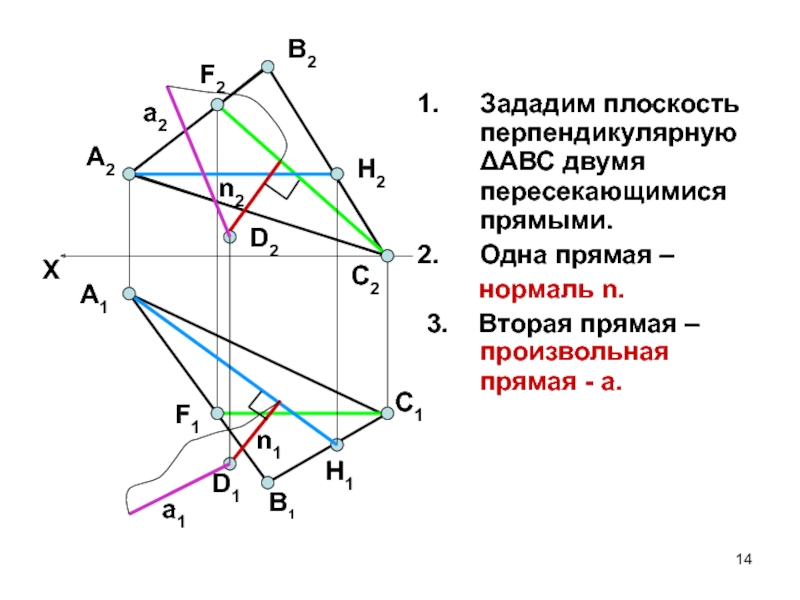
Слайд 14Зададим плоскость перпендикулярную ΔАВС двумя пересекающимися прямыми.
Одна прямая –
нормаль n.
3. Вторая прямая – произвольная
прямая - а.А2
F2
В2
А1
F1
X
H2
H1
С1
С2
n2
n1
В1
D2
D1
a1
a2
Слайд 15ПЕРЕСЕКАЮЩИЕСЯ ПРЯМАЯ И ПЛОСКОСТЬ
ПЕРЕСЕКАЮЩИЕСЯ ПЛОСКОСТИ
ПРЯМАЯ И ПЛОСКОСТЬ ПЕРЕСЕКАЮТСЯ,
ЕСЛИ У НИХ ЕСТЬ ОДНА ОБЩАЯ ТОЧКА
Слайд 16Точка пересечения прямой и плоскости частного положения определяется на пересечении
следа плоскости и проекции прямой.
X
O
a1
а2
П1
П2
К1
К2
X
O
a1
а2
П1
П2
К1
К2
Слайд 171. ПЛОСКОСТИ ПЕРЕСЕКАЮТСЯ, ЕСЛИ У НИХ ЕСТЬ ДВЕ ОБЩИЕ ТОЧКИ
2.
ДВЕ ПЛОСКОСТИ ПЕРЕСЕКАЮТСЯ ПО ПРЯМОЙ ЛИНИИ, КОТОРАЯ ПРОХОДИТ ЧЕРЕЗ ДВЕ
ОБЩИЕ ТОЧКИ ПЛОСКОСТЕЙСлайд 18Линия пересечения плоскостей определяется по точкам пересечения сторон треугольника ΔАВС
и фронтального следа плоскости α.
X
O
К2
F2
F1
К1
A2
B2
C2
B1
A1
C1
αП1
αП2
αx
Слайд 19Пересечение прямой и плоскости общего положения
1. Через прямую проводят
плоскость частного положения α ┴ П1.
2. Определяют линию пересечения
заданной плоскости ΔАВС и введенной α (DE).3. Определяют точку пересечения заданной прямой и построенной
линии пересечения DE. Это искомая точка пересечения плоскости треугольника АВС и прямой а.
4. Определяют видимость прямой а.
αП1
C1
Е2
A2
С2
B2
A1
B1
D1
E1
a1
a2
D2
αП2
Способ вспомогательных секущих плоскостей
К2
К1
αx
Слайд 20Видимость прямых определим по конкурирующим точкам. Конкурирующие точки - точки
лежащие на одном проецирующем луче.
Конкурирующие точки располагаются дальше или
ближе относительно плоскости П2.выше или ниже относительно плоскости П1
А1
С2
D2
D1Ξ C1
X
В1
А2 Ξ В2
X
Слайд 22Внешний контур всегда виден.
Если внутри контура пересекаются две прямые, то
одна из них видима, вторая- невидима. Видимость прямых определяют по
конкурирующим точкам или визуально.Если внутри контура пересекаются три прямые, то они имеют одинаковую видимость.
Правило определения видимости
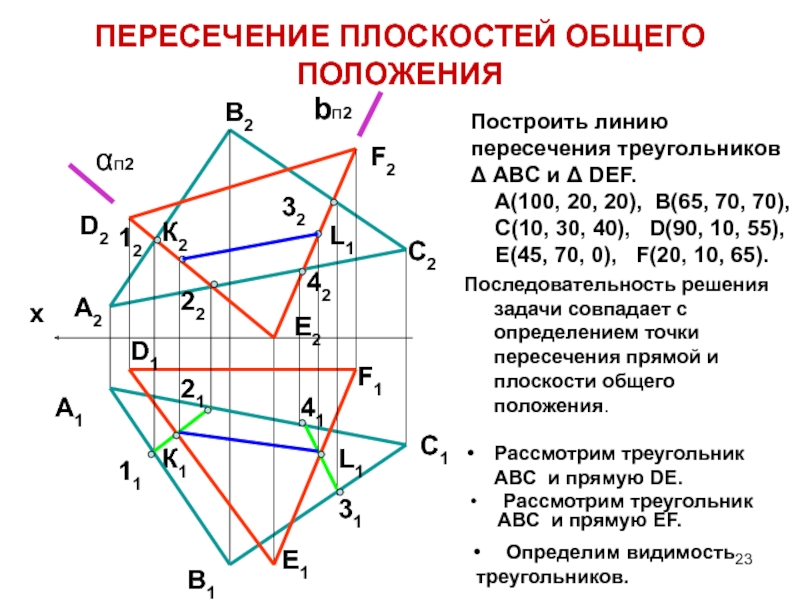
Слайд 23ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ ОБЩЕГО ПОЛОЖЕНИЯ
К1
A2
В2
С2
A1
В1
С1
D2
F2
E2
D1
F1
E1
αп2
12
22
11
21
bп2
32
42
x
41
31
L1
К2
L1
Построить линию пересечения треугольников Δ
ABC и Δ DEF.
A(100, 20, 20), B(65, 70,
70),C(10, 30, 40), D(90, 10, 55),
E(45, 70, 0), F(20, 10, 65).
Последовательность решения задачи совпадает с определением точки пересечения прямой и плоскости общего положения.
Рассмотрим треугольник АВС и прямую DE.
Рассмотрим треугольник АВС и прямую EF.
Определим видимость
треугольников.
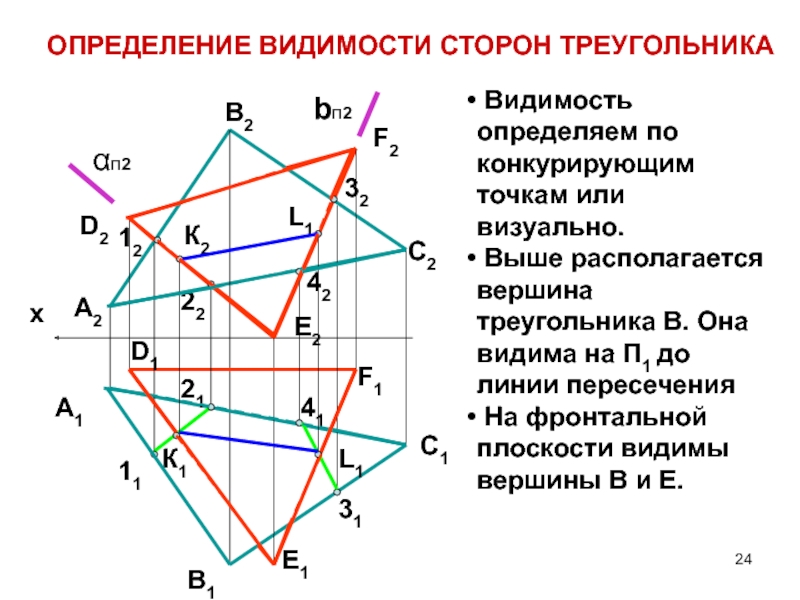
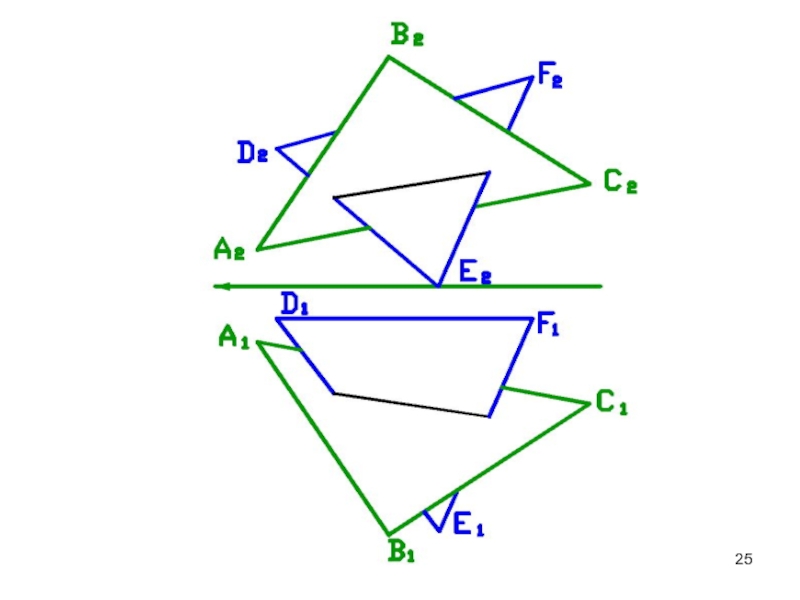
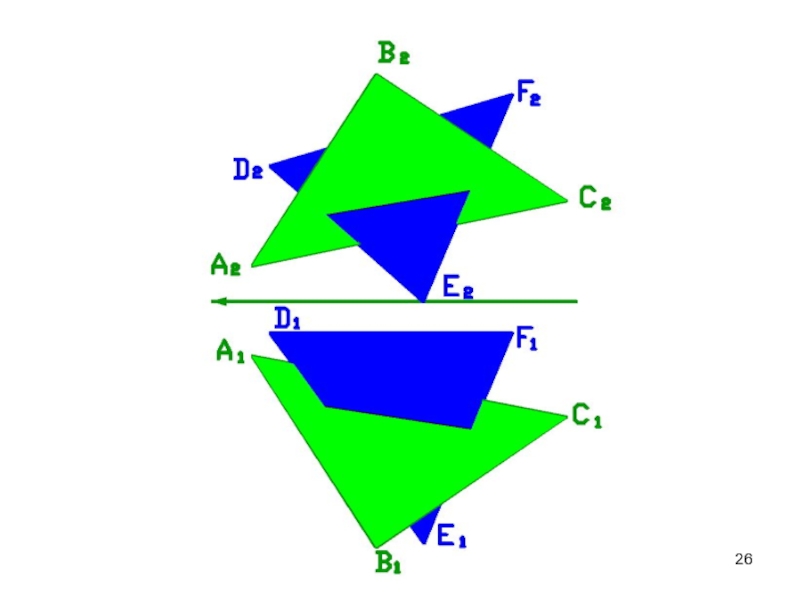
Слайд 24ОПРЕДЕЛЕНИЕ ВИДИМОСТИ СТОРОН ТРЕУГОЛЬНИКА
К1
A2
В2
С2
A1
В1
С1
D2
F2
E2
D1
F1
E1
αп2
12
22
11
21
bп2
32
42
x
41
31
L1
К2
L1
Видимость определяем по конкурирующим точкам или
визуально.
Выше располагается вершина треугольника В. Она видима на П1
до линии пересеченияНа фронтальной плоскости видимы вершины В и Е.