Перемещения деформируемых систем. Лекция 3

от силовых воздействий:

Intj
По формуле Симпсона:


Фj



Si
SF
CS



Sbj, i
Sej, i
Scj, i
Sbj, F
Sej,

F

Scj, F

CS, bj

CS, cj

CS, ej

lj

bj

ej

cj

lj /2

lj /2

В матричной форме:

=

Sj, F

BS, j

Sj, i – вектор усилий в расчётных сечениях
b, c, e j-го участка в i-ом единичном
состоянии системы ( от Fi = 1 )

Sj, F – вектор усилий в расчётных сечениях b, c, e
j-го участка в действительном ( грузовом )
состоянии системы – от заданной нагрузки

BS, j – матрица упругой податливости j-го участка
при деформации, соответствующей усилию S

от силовых воздействий:

Intj


Фj



Si
SF
CS



Sbj, i
Sej, i
Scj, i
Sbj, F
Sej, F
Scj, F
CS,

bj

CS, cj

CS, ej

bj

ej

cj

lj /2

lj /2

В матричной форме:

Sj, F

BS, j

Sj, i – вектор усилий в расчётных сечениях
b, c, e j-го участка в i-ом единичном
состоянии системы ( от Fi = 1 )

Sj, F – вектор усилий в расчётных сечениях b, c, e
j-го участка в действительном ( грузовом )
состоянии системы – от заданной нагрузки

BS, j – матрица упругой податливости j-го участка
при деформации, соответствующей усилию S

от силовых воздействий:

Intj


Фj



Si
SF
CS



Sbj, i
Sej, i
Scj, i
Sbj, F
Sej, F
Scj, F
CS,

bj

CS, cj

CS, ej

bj

ej

cj

lj /2

lj /2

Sj, i – вектор усилий в расчётных сечениях
b, c, e j-го участка в i-ом единичном
состоянии системы ( от Fi = 1 )

Sj, F – вектор усилий в расчётных сечениях b, c, e
j-го участка в действительном ( грузовом )
состоянии системы – от заданной нагрузки

BS, j – матрица упругой податливости j-го участка
при деформации, соответствующей усилию S

0

0

Si – вектор усилий S в расчётных сечениях
всех участков системы в i-ом единичном
состоянии ( от Fi = 1 )

SF – вектор усилий S в расчётных сечениях
всех участков системы в действительном
( грузовом ) состоянии – от заданной нагрузки

BS – матрица упругой податливости системы
при деформации, соответствующей усилию S

от силовых воздействий:

Intj


Фj



Si
SF
CS



Sbj, i
Sej, i
Scj, i
Sbj, F
Sej, F
Scj, F
CS,

bj

CS, cj

CS, ej

bj

ej

cj

lj /2

lj /2

0

0

Si – вектор усилий S в расчётных сечениях
всех участков системы в i-ом единичном
состоянии ( от Fi = 1 )

SF – вектор усилий S в расчётных сечениях
всех участков системы в действительном
( грузовом ) состоянии – от заданной нагрузки

BS – матрица упругой податливости системы
при деформации, соответствующей усилию S

от силовых воздействий:

Intj


Фj



Si
SF
CS



Sbj, i
Sej, i
Scj, i
Sbj, F
Sej, F
Scj, F
CS,

bj

CS, cj

CS, ej

bj

ej

cj

lj /2

lj /2

0

0

Si – вектор усилий S в расчётных сечениях
всех участков системы в i-ом единичном
состоянии ( от Fi = 1 )

SF – вектор усилий S в расчётных сечениях
всех участков системы в действительном
( грузовом ) состоянии – от заданной нагрузки

BS – матрица упругой податливости системы
при деформации, соответствующей усилию S

– вектор усилий в элементах системы
в i-ом единичном состоянии ( от Fi = 1 ) –
в расчётных сечениях

– вектор усилий в элементах системы
в действительном ( грузовом ) состоянии –
от заданной нагрузки – в расчётных сечениях

– матрица упругой податливости элементов
системы при всех видах деформаций

от силовых воздействий:

Intj


Фj



Si
SF
CS



Sbj, i
Sej, i
Scj, i
Sbj, F
Sej, F
Scj, F
CS,

bj

CS, cj

CS, ej

bj

ej

cj

lj /2

lj /2

0

0

– вектор усилий в элементах системы
в i-ом единичном состоянии ( от Fi = 1 ) –
в расчётных сечениях

– вектор усилий в элементах системы
в действительном ( грузовом ) состоянии –
от заданной нагрузки – в расчётных сечениях

– матрица упругой податливости элементов
системы при всех видах деформаций

Добавка за счёт
податливости
упругих связей

от силовых воздействий:

Intj



Si
SF
CS



Sbj, i
Sej, i
Scj, i
Sbj, F
Sej, F
Scj, F
CS,

bj

CS, cj

CS, ej

bj

ej

cj

lj /2

lj /2

0

0

– вектор усилий в элементах системы
в i-ом единичном состоянии ( от Fi = 1 ) –
в расчётных сечениях

– вектор усилий в элементах системы
в действительном ( грузовом ) состоянии –
от заданной нагрузки – в расчётных сечениях

– матрица упругой податливости элементов
системы при всех видах деформаций

Добавка за счёт
податливости
упругих связей

– вектор реакций
упругих связей в i-ом единичном состоянии ( от Fi = 1)

– вектор
реакций упругих связей в действительном
( грузовом ) состоянии – от заданной нагрузки

от силовых воздействий:

Intj



Si
SF
CS



Sbj, i
Sej, i
Scj, i
Sbj, F
Sej, F
Scj, F
CS,

bj

CS, cj

CS, ej

bj

ej

cj

lj /2

lj /2

– вектор усилий в элементах системы
в i-ом единичном состоянии ( от Fi = 1 ) –
в расчётных сечениях

– вектор усилий в элементах системы
в действительном ( грузовом ) состоянии –
от заданной нагрузки – в расчётных сечениях

– матрица упругой податливости элементов
системы при всех видах деформаций

Добавка за счёт
податливости
упругих связей

– вектор реакций
упругих связей в i-ом единичном состоянии ( от Fi = 1)

– вектор
реакций упругих связей в действительном
( грузовом ) состоянии – от заданной нагрузки

матрица податливости упругих связей

Перемещение от де-
формации элементов

от силовых воздействий:

– вектор усилий

в элементах системы
в i-ом единичном состоянии ( от Fi = 1 ) –
в расчётных сечениях

– вектор усилий в элементах системы
в действительном ( грузовом ) состоянии –
от заданной нагрузки – в расчётных сечениях

– матрица упругой податливости элементов
системы при всех видах деформаций

Добавка за счёт
податливости
упругих связей

– вектор реакций
упругих связей в i-ом единичном состоянии ( от Fi = 1)

– вектор
реакций упругих связей в действительном
( грузовом ) состоянии – от заданной нагрузки

матрица податливости упругих связей

Перемещение от де-
формации элементов

– вектор усилий в i-ом
единичном состоянии
( от Fi = 1 )

– вектор усилий
в действительном
( грузовом ) состоянии –
от заданной нагрузки

– матрица упругой
податливости системы

от силовых воздействий:
Особенности матрицы упругой податливости элементов системы

Для участка

постоянного сечения ( EIz,j = const, EAj = const, kτy,j /GAj = const ):

При изгибе

При сдвиге

При растяжении
(сжатии)

от силовых воздействий:
Частные случаи матриц усилий Sj, i ,

Sj, F и упругой податливости BS, j для участков постоянного сечения

а) обе функции ( эпюры ) Sj, i и Sj, F –
линейные

б) одна из функций ( эпюр ) Sj, i и Sj, F –
постоянная, другая – линейная

Sbj, i

Sej, i

Scj, i

lj

bj

ej

cj

lj /2

lj /2

Sbj, F

Sej, F

Si

SF

Si

SF

Scj, F

от силовых воздействий:
Правила назначения расчётных участков и расчётных сечений:

Границами

расчётных участков являются
1) места изменения жёсткости сечения СS ;
2) границы грузовых участков
в действительном ( F ) и единичном ( i ) состояниях

K

i

F

vK = ?

K

Fi = 1

1

3

7

6

2

4

5

b1

b2

b3

e1

e2

e3

b4

e4

c4

e6

b5

c5

e5

e7

b6

b7

Сечения
(1)…(16)

Назначение расчётных сечений
( для прямолинейных расчётных участков постоянной жёсткости ):
1) на незагруженном участке ( в действительном состоянии F ) – два концевых сечения ( bj и ej );
2) на участке, загруженном распределённой нагрузкой
( в действительном состоянии F ) – три сечения ( bj, cj и ej );
3) на участке с постоянными усилиями Si и SF – одно сечение cj ( посредине )

С учётом
только
изгиба

mM = 7

от силовых воздействий:
П р и м е р








2EI
EI
EA

4

м

4

3

3

cΔ

F = 20 кН

q = 10 кН/м

EA = 0,5 м –2EI;

cΔ = 0,2 м –3EI

1 1

Требуется: составить исходные матрицы
для определения угла поворота сечения 1-1

Решение: матричная формула
для вычисления перемещения:

F

i = 1

R1,F = 32,5 кН

M1= 1

N0,F = 25 кН

60

50

R1,1 = 1/8

N0,1 = – 5/12

MF
( кН*м )

0,5

M1
( м )

1

1

1

b1

e1

2

3

4

5

6

b2

e2

b3

e3

b4

e4

с3

с4

с5

Схема расчётных
участков и сечений

1

2

3

4

5

6

45

45

0,25

MF

NF

Rc,F

M1

N1

Rc,1

от силовых воздействий
( продолжение )
Определение нескольких перемещений от

нескольких вариантов нагрузок:

Fx

qconst

1

Варианты нагрузок

2

3

K

v2 = ?

v3 = ?

θK = ?

u1 = ?

qtemp

F

F

F

F1

F2

Ff

Fv

Перемеще-ние ΔiF по
вариантам
нагрузок

Перемещения
Δ1F ,…,ΔiF ,…,ΔnF
от f-го варианта
нагрузок

Матрица искомых
перемещений:

От F1= 1

От F2= 1

От Fi = 1

От Fn= 1

От 1-го
варианта
нагрузок

От f-го
варианта
нагрузок

От v-го
варианта
нагрузок

Матрица усилий в единичных
( фиктивных ) состояниях системы:

Матрица усилий
в грузовых
состояниях
системы:

От 2-го
варианта
нагрузок

Перемещения от тепловых воздействий ( от изменения температуры ):

Bt,S

– температурная податливость при деформации,
соответствующей усилию S

ΔtS – приращение температуры, вызывающее деформацию

Si

ΔtS

Bt,S

Sbj, i

Sej, i

Scj, i

ΔtS,bj

Bt,S, bj

lj

bj

ej

cj

lj /2

lj /2

ΔtS,cj

ΔtS,ej

Bt,S, cj

Bt,S, ej

По формуле Симпсона:

В матричной форме:

TS, j

Bt,S, j

Sj, i – вектор усилий в расчётных сечениях
b, c, e j-го участка в i-ом единичном
состоянии системы ( от Fi = 1 )

TS,j, – вектор приращений температур,
вызывающих свободную деформацию
в расчётных сечениях b, c, e j-го участка

Bt,S, j – матрица температурной податливости
j-го участка при деформации,
соответствующей усилию S

Перемещения от тепловых воздействий ( от изменения температуры ):

Bt,S

– температурная податливость при деформации,
соответствующей усилию S

ΔtS – приращение температуры, вызывающее деформацию

Si

ΔtS

Bt,S

Sbj, i

Sej, i

Scj, i

ΔtS,bj

Bt,S, bj

bj

ej

cj

lj /2

lj /2

ΔtS,cj

ΔtS,ej

Bt,S, cj

Bt,S, ej

По формуле Симпсона:

В матричной форме:

Bt,S, j – матрица температурной податливости
j-го участка при деформации,
соответствующей усилию S

Sj, i – вектор усилий в расчётных сечениях
b, c, e j-го участка в i-ом единичном
состоянии системы ( от Fi = 1 )

TS,j, – вектор приращений температур,
вызывающих свободную деформацию
в расчётных сечениях b, c, e j-го участка

Перемещения от тепловых воздействий ( от изменения температуры ):

Bt,S

– температурная податливость при деформации,
соответствующей усилию S

ΔtS – приращение температуры, вызывающее деформацию

Si

ΔtS

Bt,S

Sbj, i

Sej, i

Scj, i

ΔtS,bj

Bt,S, bj

bj

ej

cj

lj /2

lj /2

ΔtS,cj

ΔtS,ej

Bt,S, cj

Bt,S, ej

Вектор усилий в расчётных
сечениях b, c, e всех участков
системы в i-ом единичном
состоянии ( от Fi = 1 )

Вектор приращений температур,
вызывающих свободную деформацию
в расчётных сечениях b, c, e
всех участков

Матрица температурной податливости системы при деформации, соответствующей усилию S

Перемещения от тепловых воздействий ( от изменения температуры ):

Lt,i

– вектор единичных ( от Fi = 1 ) усилий, необходимых
для определения температурных перемещений

T – вектор приращений температур

Si

ΔtS

Bt,S

Sbj, i

Sej, i

Scj, i

ΔtS,bj

Bt,S, bj

bj

ej

cj

lj /2

lj /2

ΔtS,cj

ΔtS,ej

Bt,S, cj

Bt,S, ej

Вектор усилий в расчётных
сечениях b, c, e всех участков
системы в i-ом единичном
состоянии ( от Fi = 1 )

Вектор приращений температур,
вызывающих свободную деформацию
в расчётных сечениях b, c, e
всех участков

Матрица температурной податливости системы при деформации, соответствующей усилию S

Bt – матрица температурной податливости системы

Bt,S – температурная податливость при деформации,
соответствующей усилию S

ΔtS – приращение температуры, вызывающее деформацию

Перемещения от тепловых воздействий ( от изменения температуры ):

Lt,i

– вектор единичных ( от Fi = 1 ) усилий, необходимых
для определения температурных перемещений

T – вектор приращений температур

Si

ΔtS

Bt,S

Sbj, i

Sej, i

Scj, i

ΔtS,bj

Bt,S, bj

bj

ej

cj

lj /2

lj /2

ΔtS,cj

ΔtS,ej

Bt,S, cj

Bt,S, ej

Bt – матрица температурной податливости системы

Вектор Вектор
изгибающих моментов Mz продольных сил
в расчётных сечениях всех участков
в i–ом единичном cостоянии ( от Fi = 1 ).
My,i – аналогично Mz,i

Матрица температурной податливости системы при искривлениях элементов (участков) в плоскости x0y

Bt,nr, z – то же, в плоскости x0z (аналогично Bt,nr, y )

Матрица температурной податливости системы
при удлинениях / укорочениях элементов (участков)

Tnr,y , Tnr,z – векторы неравномерных
составляющих приращений температуры по
высоте и ширине расчётных сечений участков

T0 – вектор равномерных составляющих
приращений температуры

Частный случай – прямолинейный участок
постоянного сечения при постоянном
по длине участка температурном режиме

Перемещения от тепловых воздействий ( от изменения температуры ):

Lt,i

– вектор единичных ( от Fi = 1 ) усилий, необходимых
для определения температурных перемещений

T – вектор приращений температур

Si

ΔtS

Bt,S

Sbj, i

Sej, i

Scj, i

ΔtS,bj

Bt,S, bj

bj

ej

cj

lj /2

lj /2

ΔtS,cj

ΔtS,ej

Bt,S, cj

Bt,S, ej

Bt – матрица температурной податливости системы

Частный случай – прямолинейный участок
постоянного сечения при постоянном
по длине участка температурном режиме

Mz, j, i = [ Mz, cj, i ]

My, j, i = [ My, cj, i ]

Nj, i = [ Ncj, i ]

Δtnr,y, j = [ Δtnr,y, cj ]

Δtnr,z, j = [ Δtnr,z, cj ]

Δt0, j = [ Δt0, cj ]

2

0

z

h1

h2

Δt1

Δt2

h

3

4

b3

b4

b

Δt0

Δt3

Δt4

y

1

Перемещения от тепловых воздействий ( от изменения температуры ):

Признаки границ расчётных участков:
1) границы грузовых участков;
2) места изменения температурного режима;
3) точки изменения высоты сечения элементов;
4) места изменения материала ( коэффициента α ).

4 м

2

2

А

3

text = –24oC

tint = + 20oC

П р и м е р

Определить вертикальное
перемещение точки A

h1

h2

; h2 = 0,3 м

h1 = 0,5 м

α = 12*10 – 6 ( oC )–1

Действительное состояние системы

tinit = + 10oC

Δtint = + 10oC;

Δtext = –34oC

Δt1 = + 10oC

Δt2 = –34oC

Δt2 = + 10oC

Δt1 = –34oC

Δt0 = –12oC

Δtnr = –44oC

Δt0 = –12oC

Δtnr = +44oC

А

F1 = 1

Вспомогательное
единичное состояние
системы

1

1

1/3

1/2

M1

N1

Δtnr = Δt1 – Δt2

Δt0 = ( Δt1+ Δt2)/2

Схема
расчётных
участков

1М

2М

3М

2N

1N

Перемещения от кинематических воздействий ( смещений связей ):

– вектор

реакций
смещаемых связей
в i–ом единичном
состоянии ( от Fi = 1 )

В матричной форме:

– вектор
компонентов
заданных
смещений
связей

r

П р и м е р

А

А’

B

B’

4 м

2

2

1

1 см

0,5 см

0,8 см

0,002

K

2

Определить вертикальное перемещение точки К

Δ(1) =

Δ(2) =

= Δ(3)

= Δ(4)

K

F1 = 1

R(1),1 = – 0,5

R(3),1 = – 0,5

R(2),1 = – 1

R(4),1 = – 2

Вспомогательное
единичное состояние

Действительное
состояние системы

от комбинированных воздействий:
0
0
Вектор характеристик
заданных воздействий
Матрица
общей
податливости
системы
Вектор единичных усилий
Вариант:
Матрица характеристик

заданных воздействий

0

0

Матрица усилий от единичных воздействий
( Fi = 1, i = 1,…, n ) по направлениям
искомых перемещений

Матрица характеристик заданных воздействий
по вариантам ( f = 1,…, v )

Несколько (n) перемещений
от нескольких (v) вариантов воздействий:

два различных состояния ЛДС
при механических воздействиях (силовых и/или кинематических)
1.

Теорема о взаимности возможных работ ( теорема Бетти )
E. Betti, 1872

Fi

Fk

Состояние

Состояние

i

k

Fi , Fk – обобщённые нагрузки i–го и k–го состояний ЛДС

Возможная работа внешних (внутренних) сил i -го состояния системы на
перемещениях (деформациях) k -го состояния равна возможной работе внешних
(внутренних) сил k -го состояния на перемещениях (деформациях) i-го состояния:

Д о к а з а т е л ь с т в о:

Wext, ik = Wext, ki

Wint, ik = Wint, ki

=

Wint, ik = –Wext, ik

Wint, ki = –Wext, ki

два различных состояния ЛДС
при механических воздействиях (силовых и/или кинематических)
2.

Теорема о взаимности единичных перемещений
( теорема Максвелла ) J.C. Maxwell, 1864

Fi = 1

Единичноесостояние

i

k

Перемещение δik по направлению силы*) i -го состояния от единичной силы*)
k -го состояния ( от Fk = 1 ) равно перемещению δki по направлению
cилы k -го состояния от единичной силы i -го состояния ( от Fi = 1 ):

Д о к а з а т е л ь с т в о:

δik = δki

Fi * δik = Fk * δki

Fk = 1

Единичноесостояние

a

b

a

b

δik

δki

По теореме Бетти: Wext, ik = Wext, ki

1 * δik = 1 * δki

*) в общем случае – обобщённой

два различных состояния ЛДС
при механических воздействиях (силовых и/или кинематических)
3.

Теорема о взаимности единичных реакций
( теорема Рэлея ) J.W. Rayleigh

Zi = 1

Единичноесостояние

i

k

Реакция rik i – й связи от единичного смещения k – й связи ( от Zk = 1 )
равна реакции rki k – й связи от единичного смещения i – й связи ( от Zi = 1 ):

Д о к а з а т е л ь с т в о:

rik = rki

rki * Zk = rik * Zi

Zk = 1

Единичноесостояние

rik

rki

По теореме Бетти: Wext, ik = Wext, ki

rki * 1 = rik* 1

i

k

i

k

два различных состояния ЛДС
при механических воздействиях (силовых и/или кинематических)
4.

Теорема о взаимности единичных реакций и перемещений
( теорема Гвоздева ) А.А. Гвоздев, 1927

Zi = 1

Единичноесостояние

i

Реакция i – й связи от единичной силы k – го состояния ( от Fk = 1 )
численно равна, но противоположна по знаку перемещению
по направлению этой силы, возникающему в i – ом состоянии
от единичного смещения i – й связи ( от Zi = 1 ):

Д о к а з а т е л ь с т в о:

По теореме Бетти: Wext, ik = Wext, ki

i

k

Fk = 1

Единичноесостояние

b

i

b

е в о п р о с ы
( в

скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 29» )
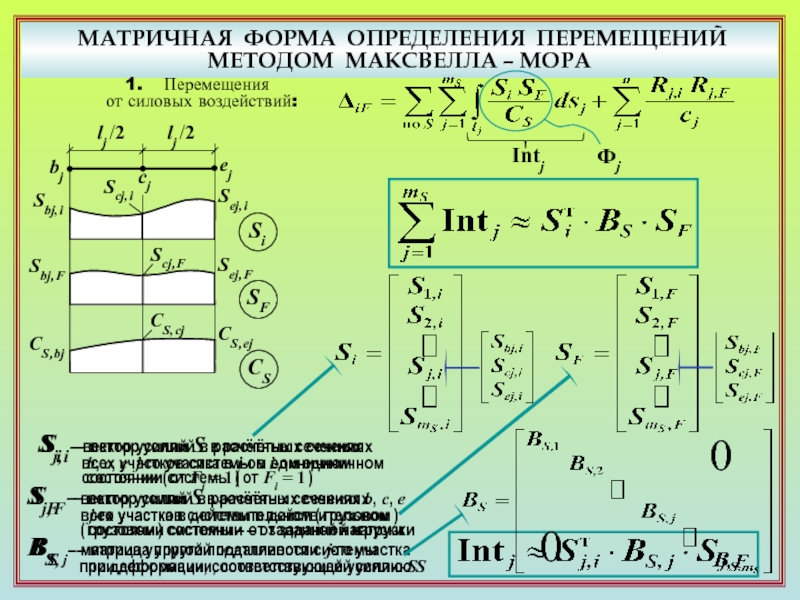
1. Какой приём вычисления интегралов в формуле Максвелла – Мора используется
для получения матричного выражения перемещения от силовых воздействий? ( 2 )
2. Записать матричную формулу для определения одного перемещения ΔiF от одного
варианта заданных нагрузок. ( 9 )
3. Как формируется вектор усилий в единичном или грузовом состоянии для расчётного
участка и системы в целом ( общий случай )? ( 2 – 6 )
4. Какой вид имеет матрица упругой податливости расчётного участка и всей системы
при определённом виде деформации ( общий случай )? ( 2 – 4 )
5. Как согласуются по размерам и последовательности расположения блоки векторов
единичных и грузовых усилий и матрицы упругой податливости, соответствующие
различным участкам и видам деформации? ( 4 – 6 )
6. Какие части векторов усилий и матрицы упругой податливости системы относятся
к учёту деформаций дискретных упругоподатливых связей? ( 7 – 9 )
7. Правила назначения расчётных участков и расчётных сечений для матричного
вычисления перемещений от силовых воздействий. ( 13 )
8. Частные случаи матриц усилий и упругой податливости для участков постоянного
сечения. ( 12 )
9. Какую структуру имеют матрицы единичных усилий и усилий от заданных нагрузок
при определении нескольких перемещений от нескольких вариантов загружений? ( 15 )
10. Зависит ли матрица упругой податливости системы от числа искомых перемещений
и вариантов нагрузок? ( 15 )
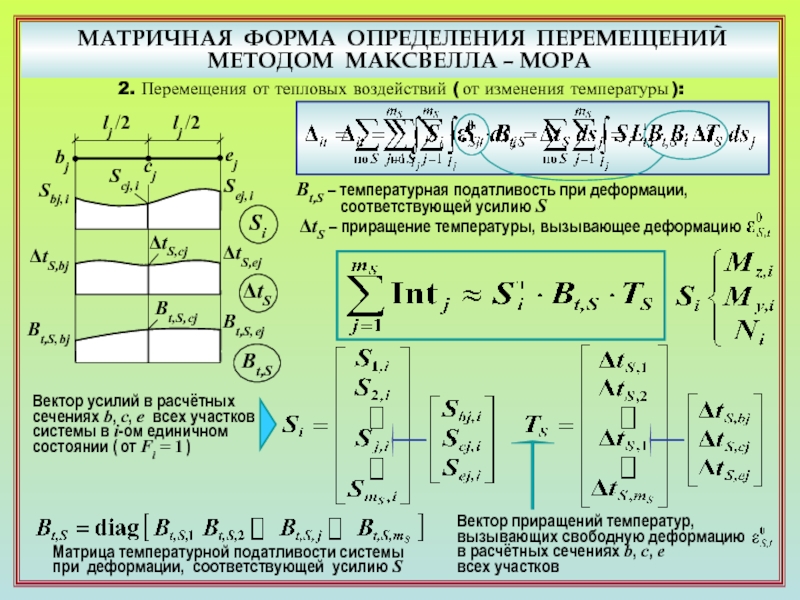
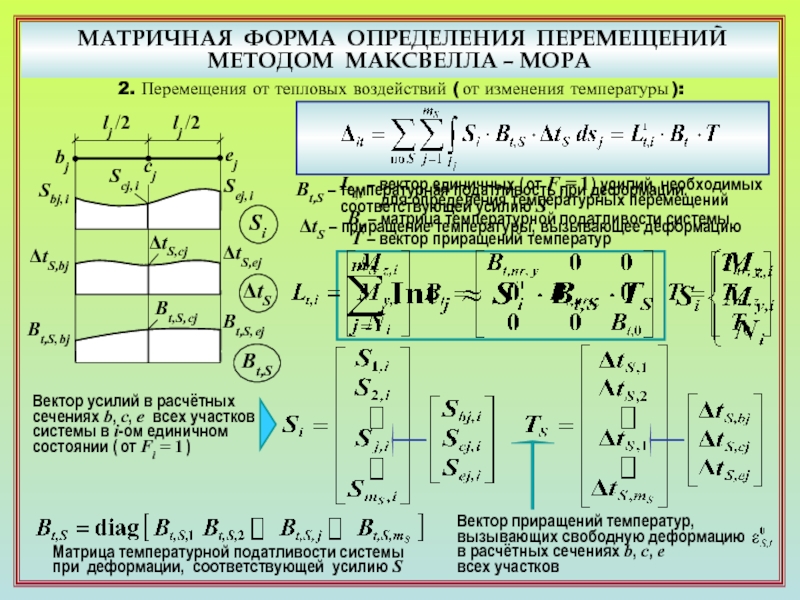
11. По какой матричной формуле определяется перемещение от изменения температуры?
( 19 ) ( 19 ) ( 22 )
_____________________________________________________
*) Только в режиме «Показ слайдов»

е в о п р о с ы
( в

скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 30» )
12. Какие силовые факторы входят в матрицу ( вектор ) единичных усилий
при определении температурных перемещений в пространственной системе?
В случае плоской системы? ( 20 )
13. Из каких частей состоит вектор приращений температур ( как учитываются неравномерная и равномерная температурные составляющие )? ( 20 )
14. Какова структура матрицы температурной податливости в случаях пространственной
и плоской систем? ( 20 )
15. Особенности матриц единичных усилий, приращений температур и температурной податливости для участков постоянного сечения с неизменным по длине температурным режимом. ( 21 )
16. Матричная формула для перемещения от кинематических воздействий. Структура векторов единичных реакций и компонентов заданных смещений связей. ( 23 )
17. Формула для определения перемещений от комбинированных воздействий, её варианты
для суммарного перемещения и отдельных составляющих от разных видов воздействий.
( 24 )
18. Общий вид матричной формулы для определения нескольких перемещений
от нескольких вариантов комбинированных воздействий. ( 24 )
19. Теоремы о линейно деформируемых системах – что является общим в их условиях? ( 25 )
20. Дать формулировку теоремы о взаимности возможных работ ( теоремы Бетти ). ( 25 )
21. Теоремы о взаимности параметров единичных состояний ЛДС
( теоремы Максвелла ( 26 )теоремы Максвелла ( 26 ) , Рэлея ( 27 )теоремы Максвелла ( 26 ) , Рэлея ( 27 ) и Гвоздева ( 28 ) ).
_____________________________________________________
*) Только в режиме «Показ слайдов»