Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Пересечение поверхности и плоскости. Сечение поверхностей 2-го порядка
Содержание
- 1. Пересечение поверхности и плоскости. Сечение поверхностей 2-го порядка
- 2. В результате сечения поверхности плоскостью
- 3. СЕЧЕНИЕ ГРАННЫХ ПОВЕРХНОСТЕЙСечение гранной поверхности – многоугольник,
- 4. СЕЧЕНИЯ ЦИЛИНДРА ВРАЩЕНИЯ1. abi – окружность2. b^ i – эллипс3. g ll i - прямоугольникL2i2i1L1aп2bп2gп111211222
- 5. Сечение цилиндра эллипс b^ i СЕЧЕНИЯ ЦИЛИНДРА ВРАЩЕНИЯbп211212111122112212122213233131131231411424141241451552152bп2
- 6. СЕЧЕНИЯ КОНУСА ВРАЩЕНИЯ ПЛОСКОСТЬЮ1. abi – окружность2.
- 7. 4. m – гипербола m ll I5.h – парабола h ll LL2L1i2i1SСЕЧЕНИЯ КОНУСА ВРАЩЕНИЯ ПЛОСКОСТЬЮmп1hп2
- 8. СЕЧЕНИЕ КОНУСА ВРАЩЕНИЯ эллипс2212321121αп2Rк31131Rк4141142123113121122232
- 9. 121142322221414113113112132142122112313414
- 10. Пересечение прямой линии с поверхностью конусаНахождение точек пересечения строится методом вспомогательных секущих плоскостейm2m112112221RRαп2
- 11. СЕЧЕНИЯ СФЕРЫ Сечение сферы плоскостью –
- 12. СЕЧЕНИЕ СФЕРЫ плоскостьюαп212112221323131142bп241141gп25251511
- 13. ВЗАМНОЕ ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ
- 14. Линия пересечения поверхностей - совокупность точек одновременно принадлежащих двум пересекающимся поверхностям
- 15. Характер линии пересечения зависит от вида поверхностейЛиния пересечения многогранников ломаная линия
- 16. Линия пересечения двух поверхностей второго порядка -
- 17. Алгоритм решения задач на построение линии пересечения
- 18. 2. Определить характерные (опорные) точки линии пересеченияточки
- 19. 3. Провести вспомогательную секущую плоскость частного положения
- 20. 6. Соединить линией, полученные точки
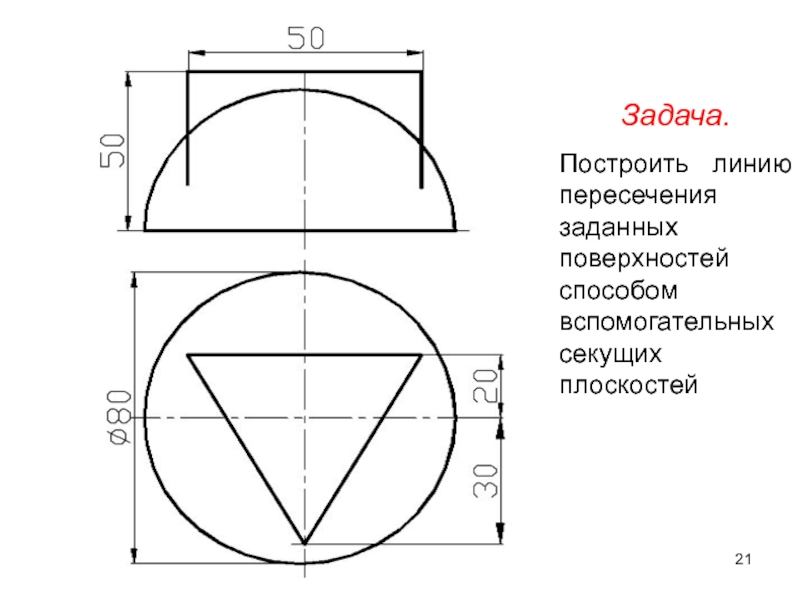
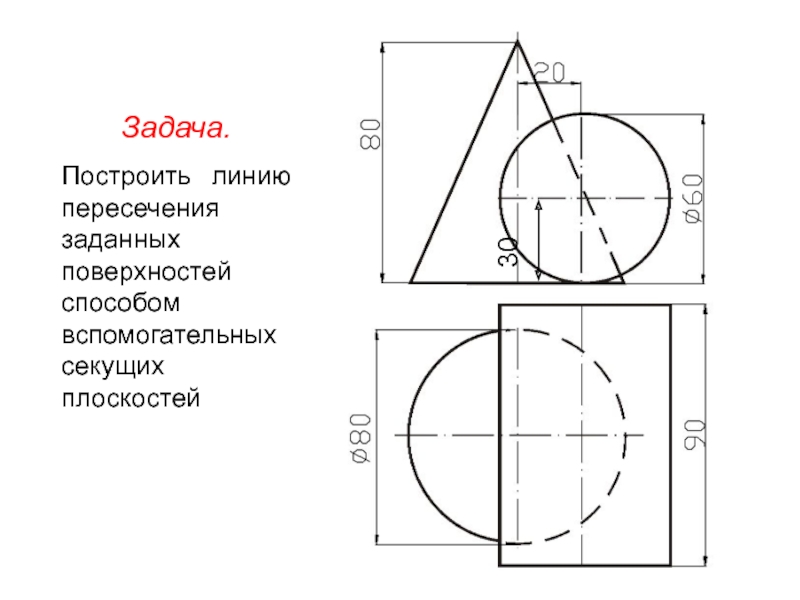
- 21. Задача. Построить линию пересечения заданных поверхностей способом вспомогательных секущих плоскостей
- 22. 1. Провести анализ данных поверхностейПересекаются призма и
- 23. п1Rc1122122142324131bп1Rc5152п16171627201022. Определить опорные точки.На фигуре треугольника
- 24. Слайд 24
- 25. Задача. Построить линию пересечения заданных поверхностей способом вспомогательных секущих плоскостей
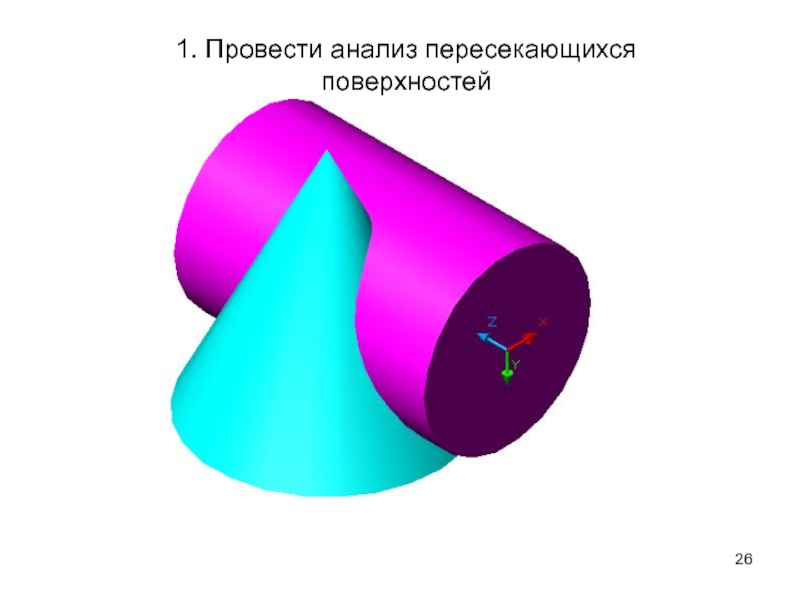
- 26. 1. Провести анализ пересекающихся поверхностей
- 27. Линия пересечения заданных поверхностей на фронтальной плоскости
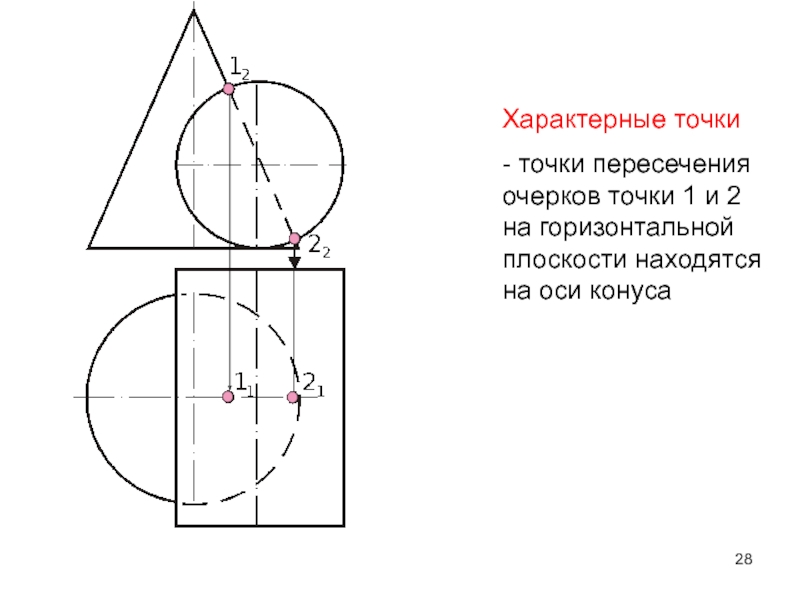
- 28. Характерные точки- точки пересечения очерков точки 1 и 2 на горизонтальной плоскости находятся на оси конуса
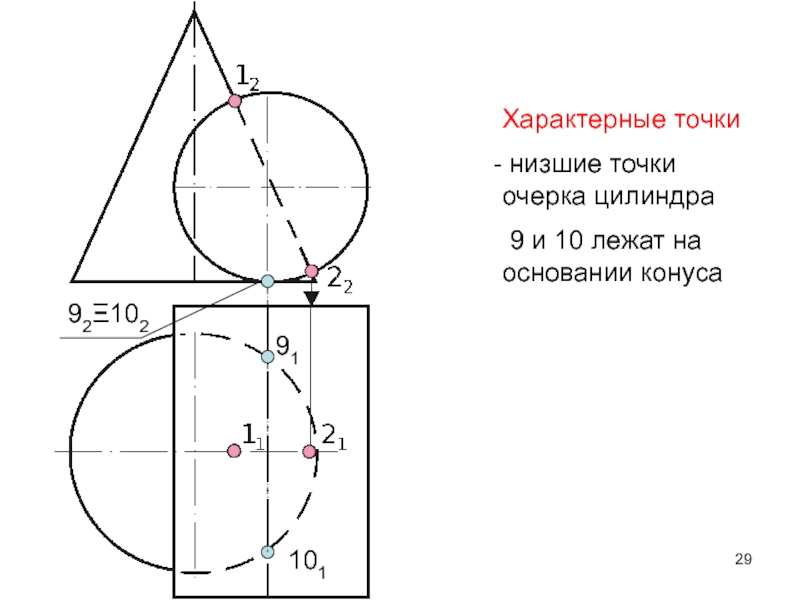
- 29. Характерные точки низшие точки очерка цилиндра 9 и 10 лежат на основании конуса92Ξ10291101
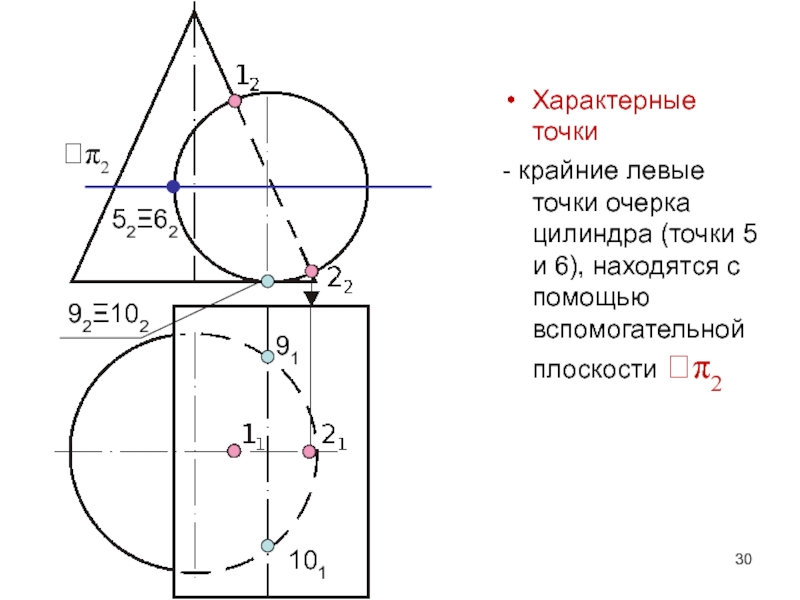
- 30. Характерные точки- крайние левые точки очерка цилиндра
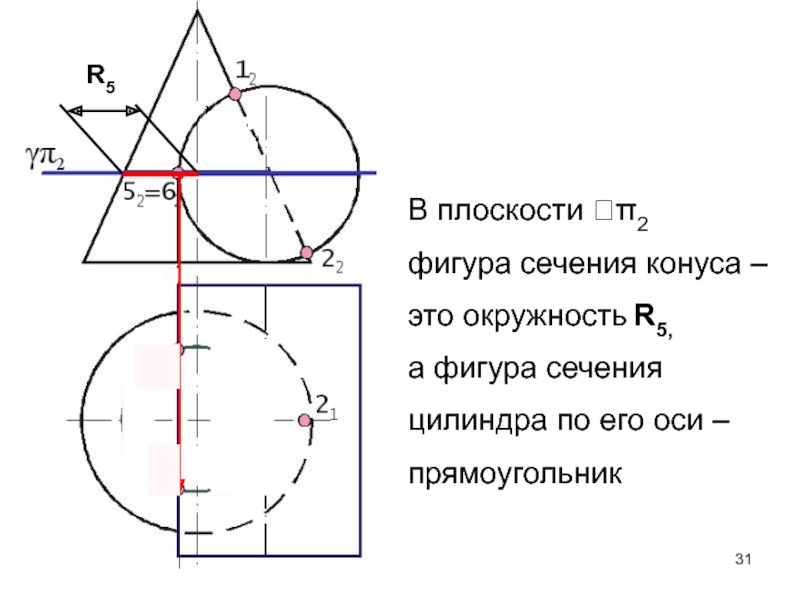
- 31. R5В плоскости π2 фигура сечения конуса –это
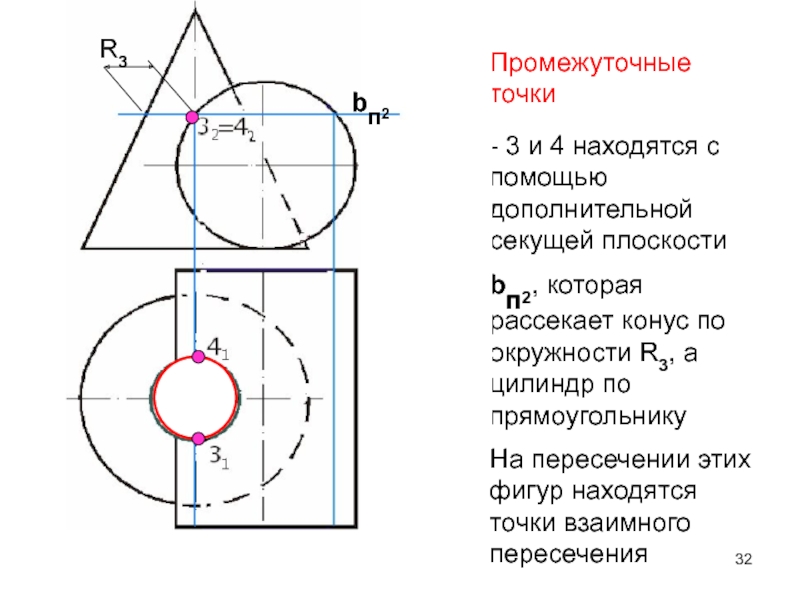
- 32. Промежуточные точки - 3 и 4 находятся
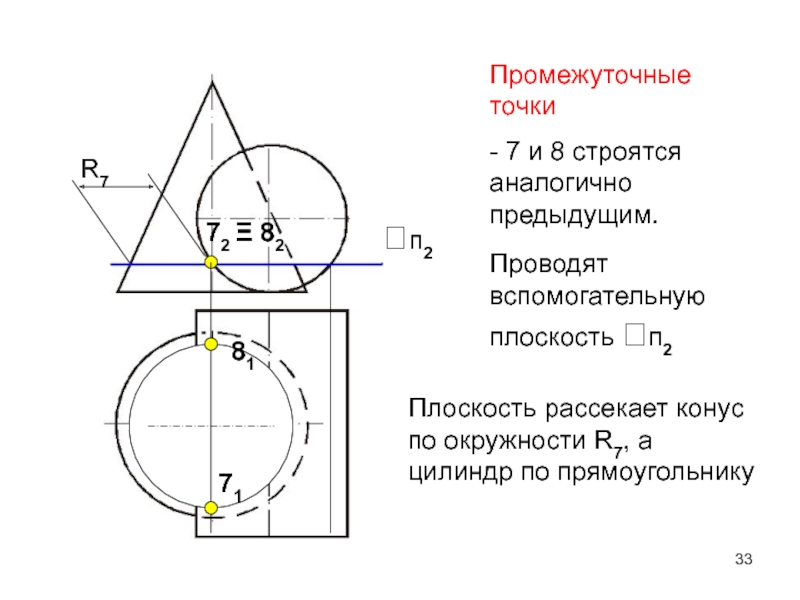
- 33. Промежуточные точки - 7 и 8 строятся
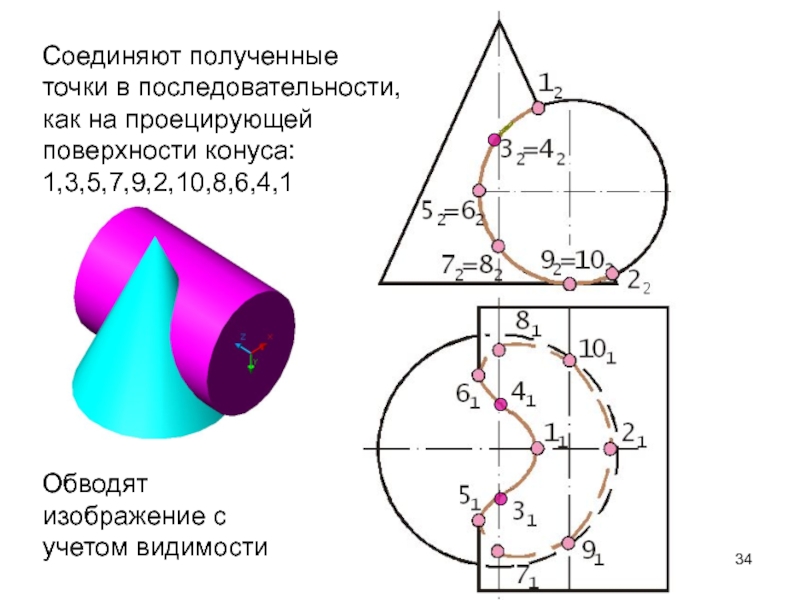
- 34. Соединяют полученные точки в последовательности, как на проецирующей поверхности конуса: 1,3,5,7,9,2,10,8,6,4,1Обводят изображение с учетом видимости
- 35. Скачать презентанцию
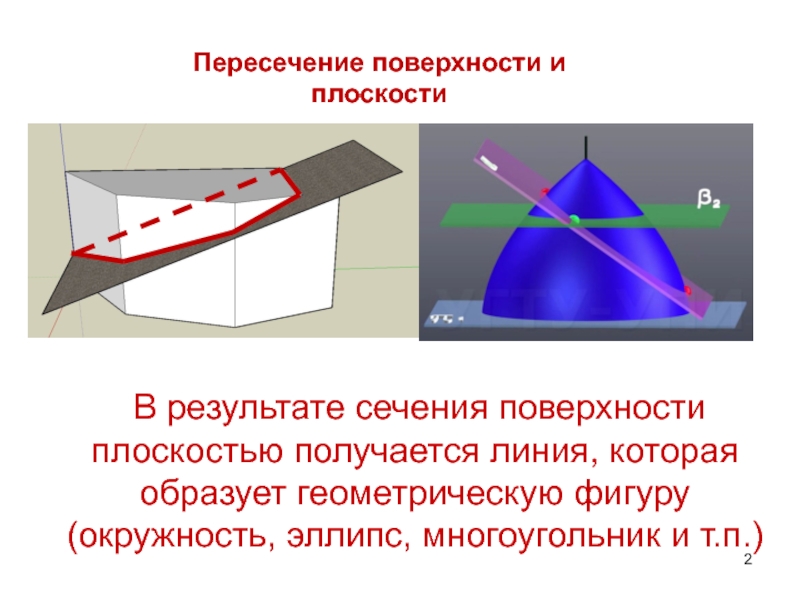
В результате сечения поверхности плоскостью получается линия, которая образует геометрическую фигуру (окружность, эллипс, многоугольник и т.п.)Пересечение поверхности и плоскости
Слайды и текст этой презентации
Слайд 1Пересечение поверхности и плоскости. Сечение поверхностей 2-го порядка
Построение линий
пересечения поверхностей
Слайд 2 В результате сечения поверхности плоскостью получается линия, которая
образует геометрическую фигуру (окружность, эллипс, многоугольник и т.п.)
Пересечение поверхности и
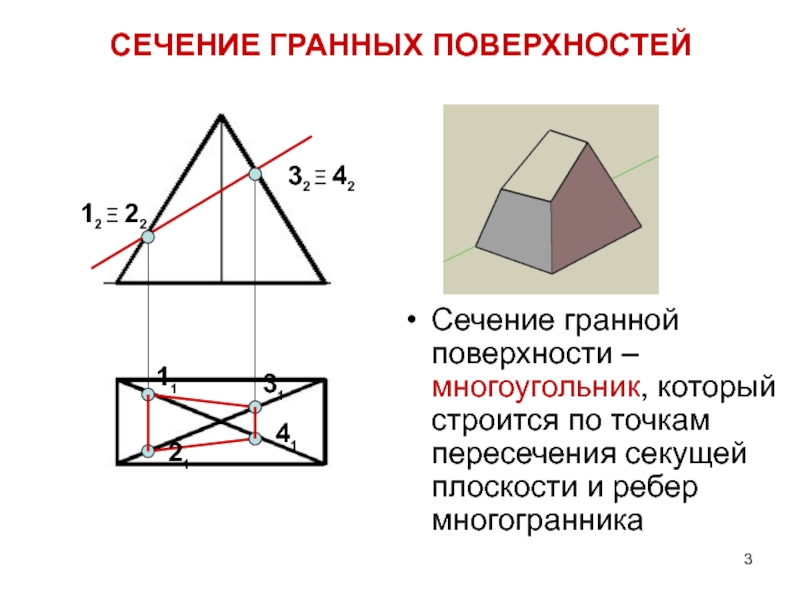
плоскости
Слайд 3СЕЧЕНИЕ ГРАННЫХ ПОВЕРХНОСТЕЙ
Сечение гранной поверхности – многоугольник, который строится по
точкам пересечения секущей плоскости и ребер многогранника
12 Ξ 22
32 Ξ
4211
21
41
31
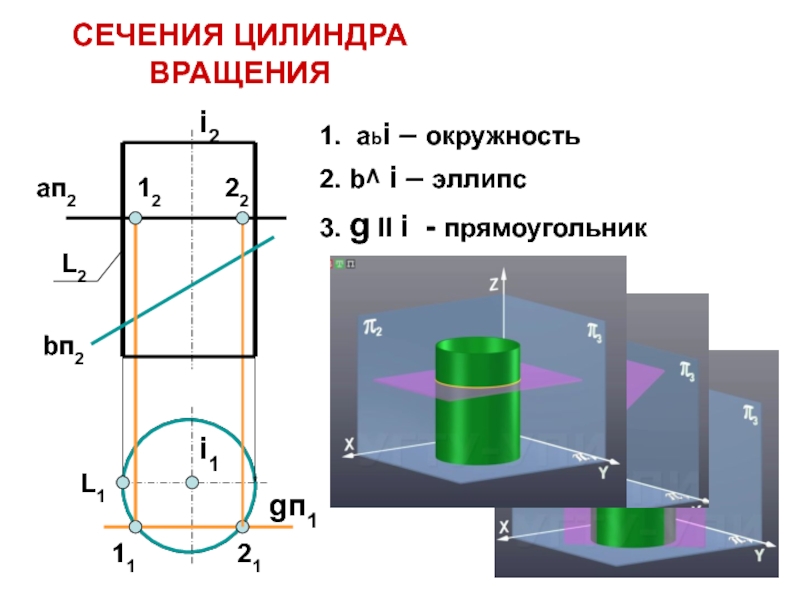
Слайд 4СЕЧЕНИЯ ЦИЛИНДРА ВРАЩЕНИЯ
1. abi – окружность
2. b^ i – эллипс
3.
g ll i - прямоугольник
L2
i2
i1
L1
aп2
bп2
gп1
11
21
12
22
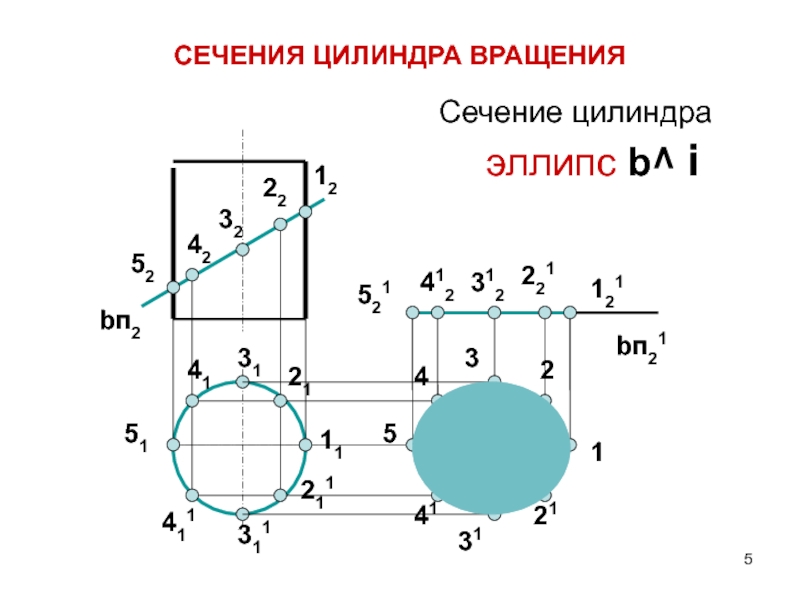
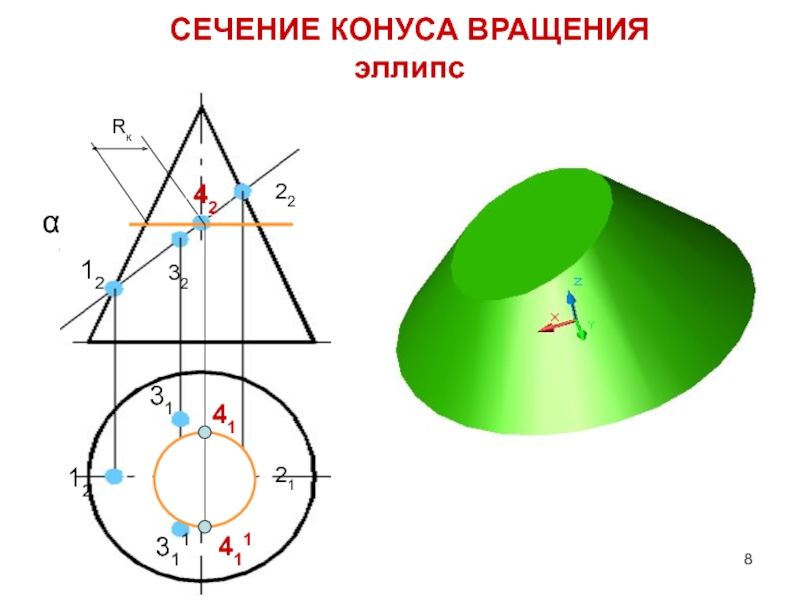
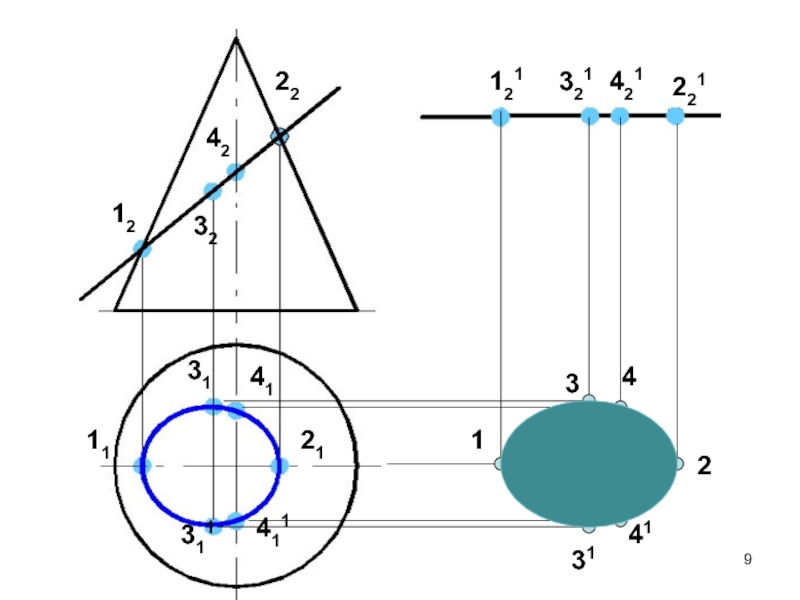
Слайд 5Сечение цилиндра
эллипс b^ i
СЕЧЕНИЯ ЦИЛИНДРА ВРАЩЕНИЯ
bп21
12
121
11
1
2
211
221
21
22
21
32
3
31
311
312
31
411
42
41
412
41
4
51
5
521
52
bп2
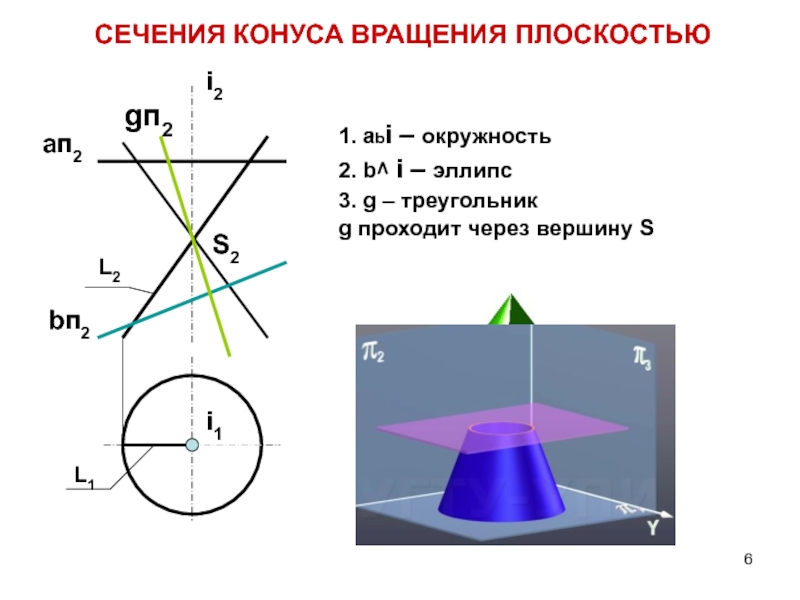
Слайд 6СЕЧЕНИЯ КОНУСА ВРАЩЕНИЯ ПЛОСКОСТЬЮ
1. abi – окружность
2. b^ i –
эллипс
3. g – треугольник
g проходит через вершину S
L2
L1
i2
i1
S2
aп2
bп2
gп2
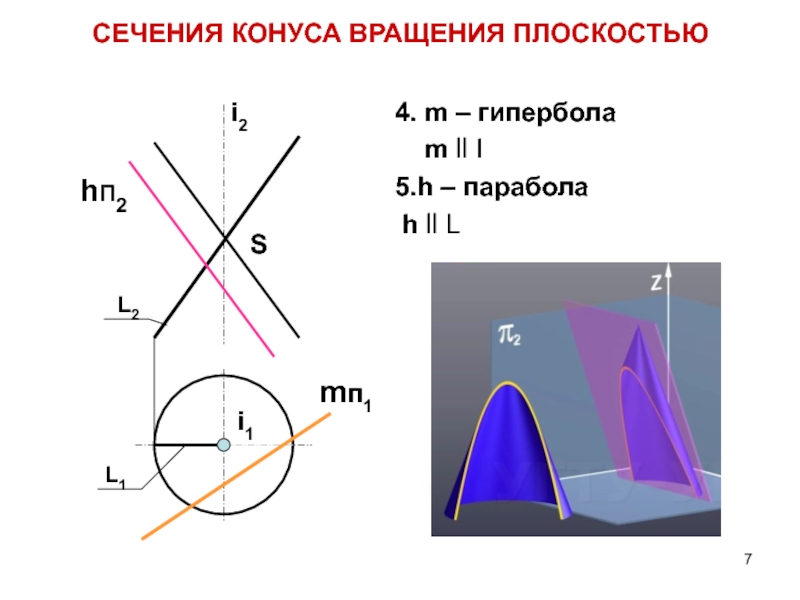
Слайд 74. m – гипербола
m ll I
5.h – парабола
h ll L
L2
L1
i2
i1
S
СЕЧЕНИЯ КОНУСА ВРАЩЕНИЯ ПЛОСКОСТЬЮ
mп1
hп2
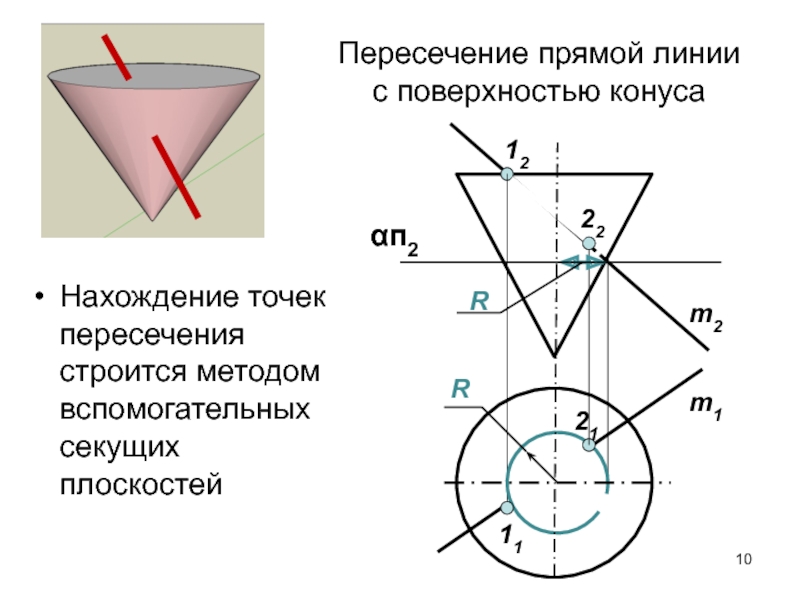
Слайд 10Пересечение прямой линии с поверхностью конуса
Нахождение точек пересечения строится методом
вспомогательных секущих плоскостей
m2
m1
12
11
22
21
R
R
αп2
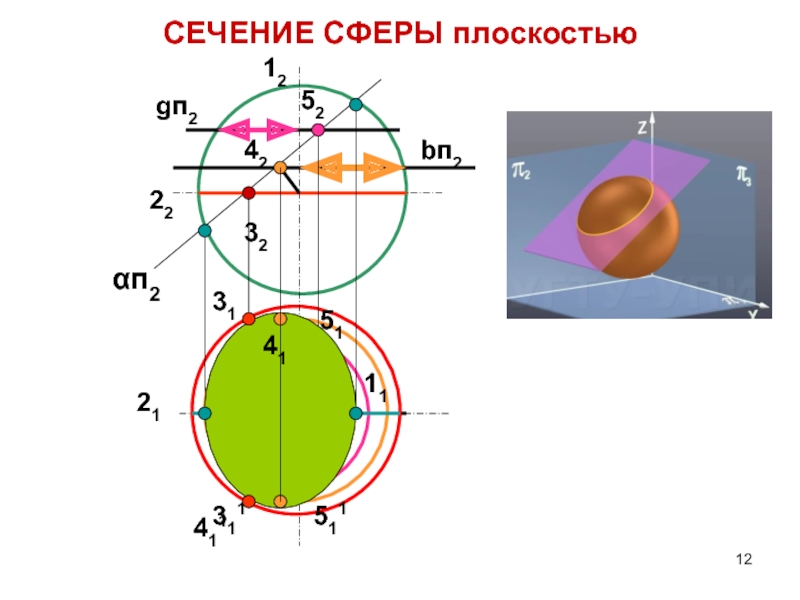
Слайд 11СЕЧЕНИЯ СФЕРЫ
Сечение сферы плоскостью – окружность, которая может
проецироваться как:
- прямая линия
- окружность- эллипс
Слайд 14Линия пересечения поверхностей -
совокупность точек одновременно принадлежащих
двум пересекающимся поверхностям
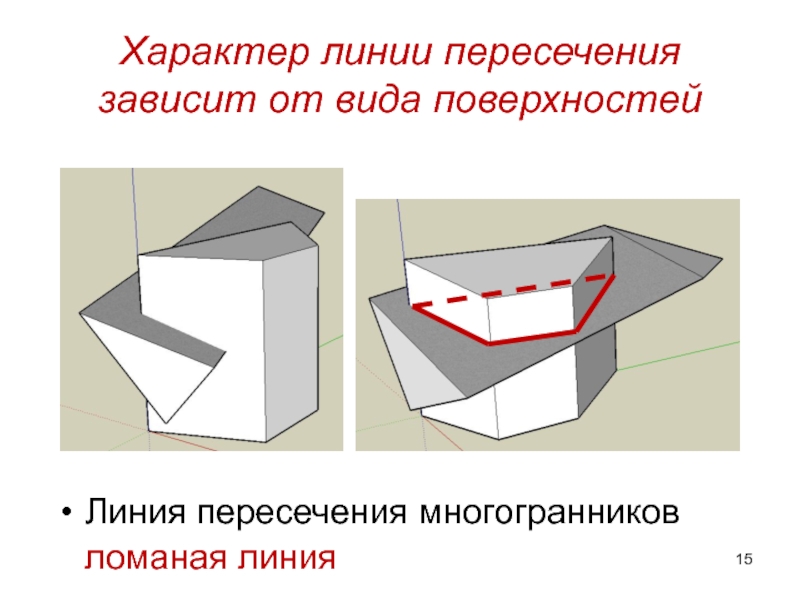
Слайд 15Характер линии пересечения зависит от вида поверхностей
Линия пересечения многогранников
ломаная линия
Слайд 16
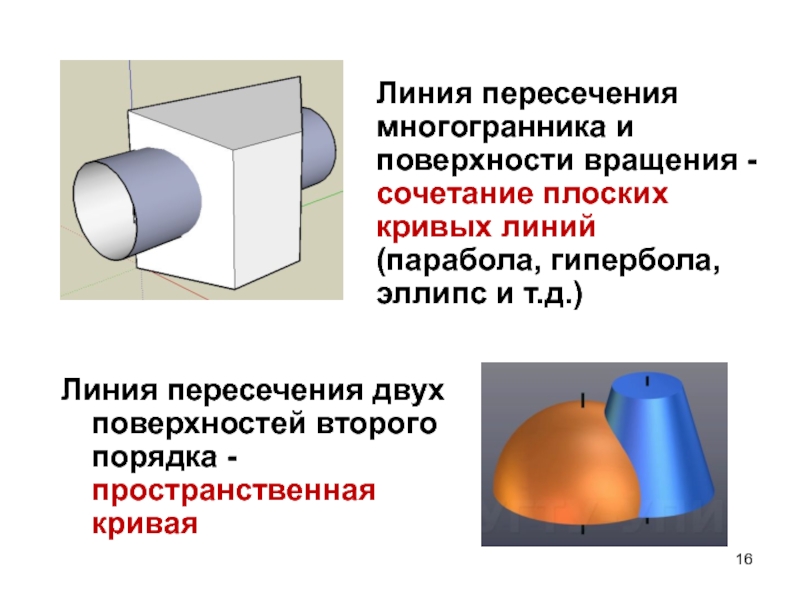
Линия пересечения двух поверхностей второго порядка - пространственная кривая
Линия пересечения
многогранника и поверхности вращения - сочетание плоских кривых линий (парабола,
гипербола, эллипс и т.д.)
Слайд 17Алгоритм решения задач на построение линии пересечения поверхностей
1. Провести анализ
заданных поверхностей
- Определить характер заданных поверхностей (цилиндр, призма, сфера,
пирамида и т.д.)Определить какая из них является проецирующей поверхностью
На плоскости проекций, к которой поверхность перпендикулярна, проекция линии пересечения совпадает с очерком проецирующей поверхности
Слайд 182. Определить характерные (опорные) точки линии пересечения
точки пересечения очерков поверхностей
высшие
и низшие, правые и левые точки поверхностей
наиболее удаленные и приближенные
к плоскостям проекций точкиточки принадлежащие очерковым линиям поверхностей
Слайд 193. Провести вспомогательную секущую плоскость частного положения между опорными точками.
В сечении поверхностей должны получаться простые геометрические
фигуры – окружности, треугольники, прямоугольники.4. Построить сечения заданных поверхностей вспомогательной секущей плоскостью. Определить точки пересечения построенных сечений.
5. Обозначить искомые точки линии пересечения поверхностей.
Повторение пунктов 3,4,5 – n раз
Слайд 20
6. Соединить линией, полученные точки пересечения. Сохранить
последовательность соединения точек, как на проецирующей поверхности
7. Определить видимость линии
пересечения и очерковых линий заданных поверхностей8. Обвести изображение данных поверхностей с учетом видимости изображения оставляя линии построения
Слайд 21Задача.
Построить линию пересечения заданных поверхностей способом вспомогательных секущих плоскостей
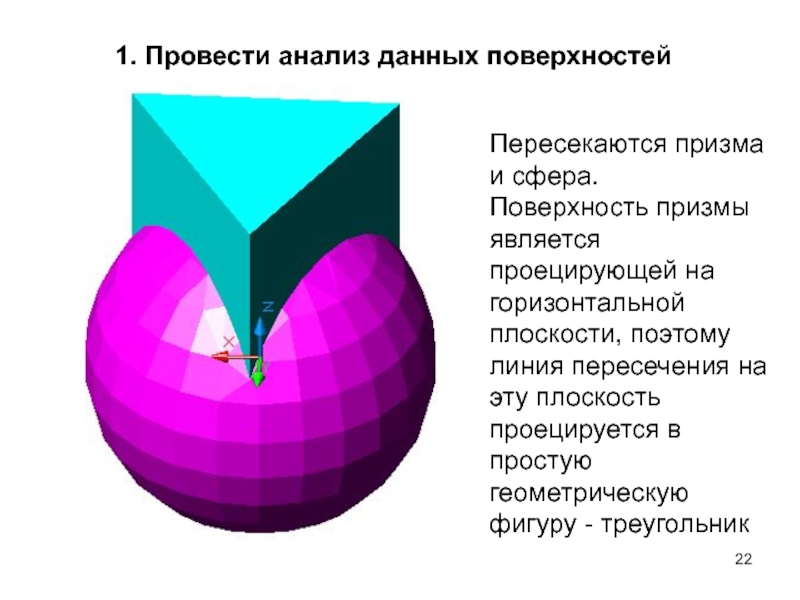
Слайд 221. Провести анализ данных поверхностей
Пересекаются призма и сфера.
Поверхность призмы является
проецирующей на горизонтальной плоскости, поэтому линия пересечения на эту плоскость
проецируется в простую геометрическую фигуру - треугольник
Слайд 23 п1
Rc
11
22
12
21
42
32
41
31
bп1
Rc
51
52
п1
61
71
62
72
01
02
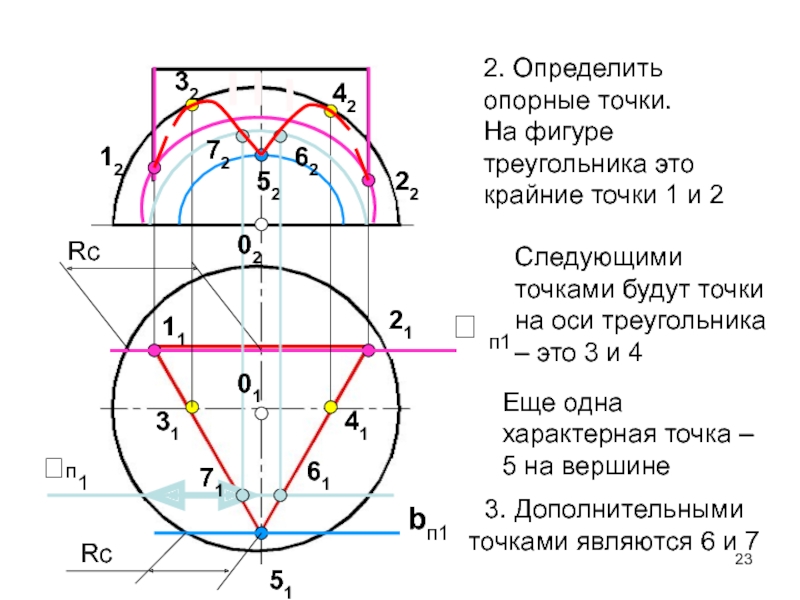
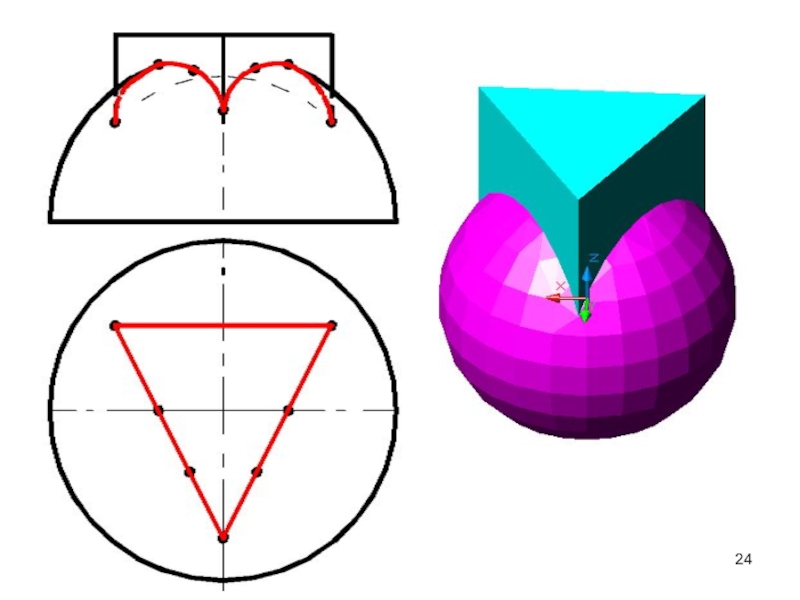
2. Определить опорные точки.
На фигуре треугольника это крайние точки
1 и 2
Следующими точками будут точки на оси треугольника –
это 3 и 4Еще одна характерная точка – 5 на вершине
3. Дополнительными точками являются 6 и 7
Слайд 25Задача.
Построить линию пересечения заданных поверхностей способом вспомогательных секущих плоскостей
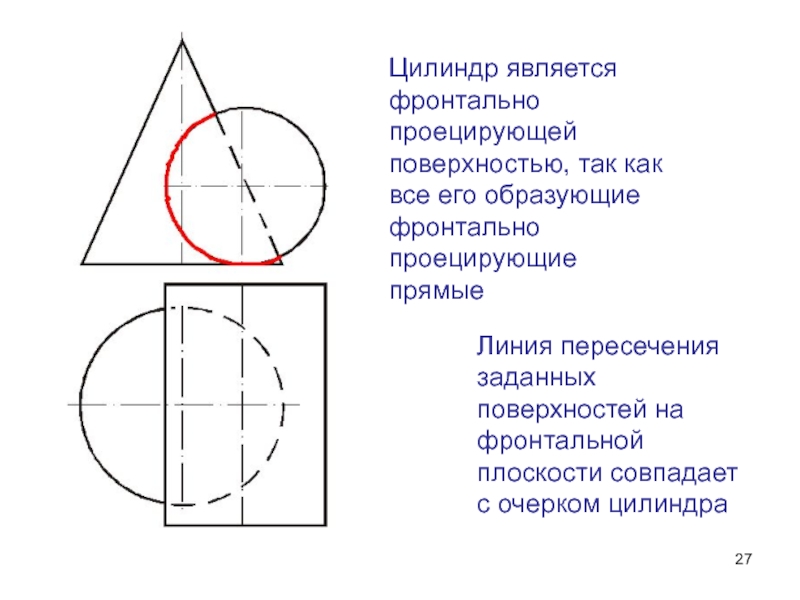
Слайд 27Линия пересечения заданных поверхностей на фронтальной плоскости совпадает с очерком
цилиндра
Цилиндр является фронтально проецирующей поверхностью, так как все его образующие
фронтально проецирующие прямые
Слайд 28Характерные точки
- точки пересечения очерков точки 1 и 2 на
горизонтальной плоскости находятся на оси конуса
Слайд 30Характерные точки
- крайние левые точки очерка цилиндра (точки 5 и
6), находятся с помощью вспомогательной плоскости π2
π2
52Ξ62
Слайд 31R5
В плоскости π2
фигура сечения конуса –
это окружность R5,
а
фигура сечения
цилиндра по его оси –
прямоугольник
Слайд 32Промежуточные точки
- 3 и 4 находятся с помощью дополнительной
секущей плоскости bп2, которая рассекает конус по окружности R3, а
цилиндр по прямоугольникуbп2
R3
На пересечении этих фигур находятся точки взаимного пересечения
Слайд 33Промежуточные точки
- 7 и 8 строятся аналогично предыдущим.
Проводят вспомогательную
плоскость п2
R7
81
71
72 Ξ 82
п2
Плоскость рассекает конус по окружности R7, а
цилиндр по прямоугольнику
Слайд 34Соединяют полученные точки в последовательности, как на проецирующей поверхности конуса:
1,3,5,7,9,2,10,8,6,4,1
Обводят изображение с учетом видимости
