Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Персептрони, дослідження в області нейронних мереж. Модель нейронної мережі зі
Содержание
- 1. Персептрони, дослідження в області нейронних мереж. Модель нейронної мережі зі
- 2. Основні визначенняГіпотеза компактності: образам відповідають компактні множини
- 3. Адаптація та навчанняАдаптація — це процес зміни
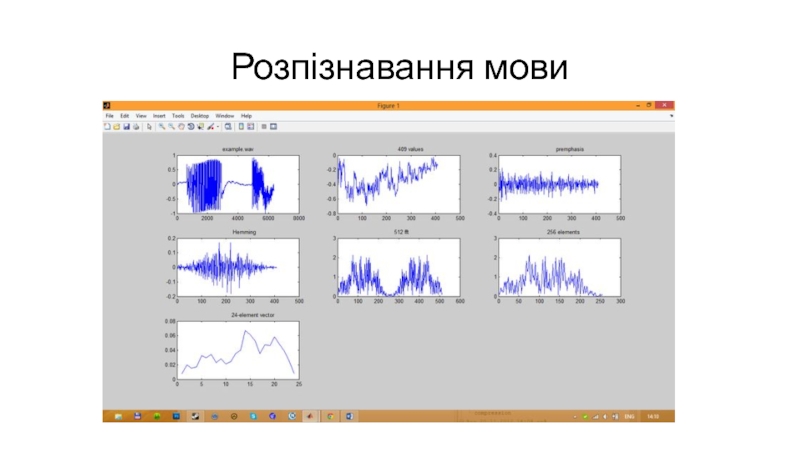
- 4. Розпізнавання мови
- 5. Розпізнавання обличчя
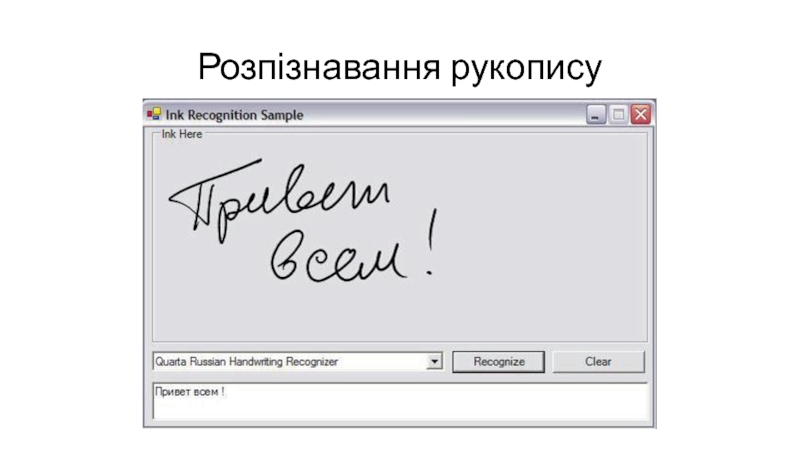
- 6. Розпізнавання рукопису
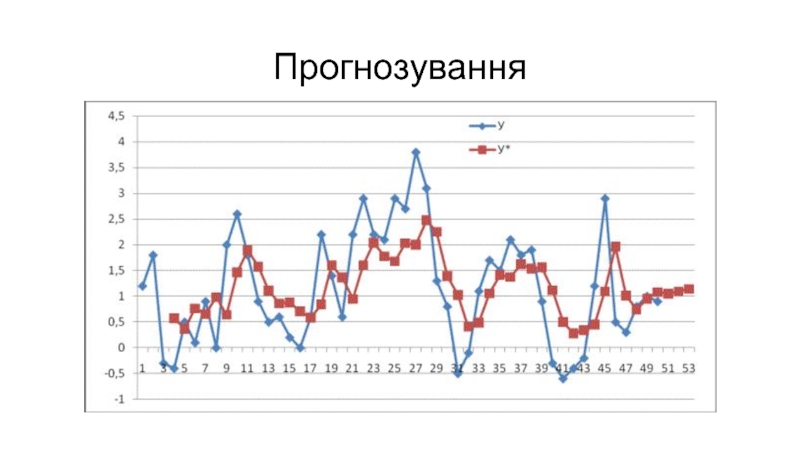
- 7. Прогнозування
- 8. Керування
- 9. Керування
- 10. Правила ХеббаПерше правило Хебба — Якщо сигнал перцептрона
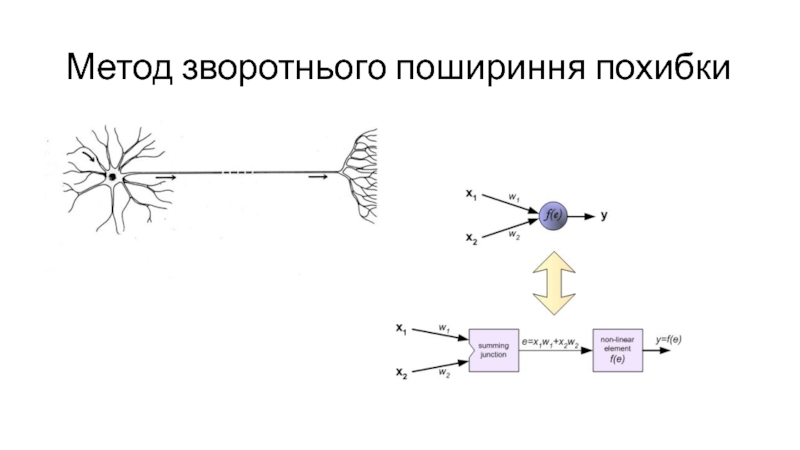
- 11. Метод зворотнього пошириння похибки
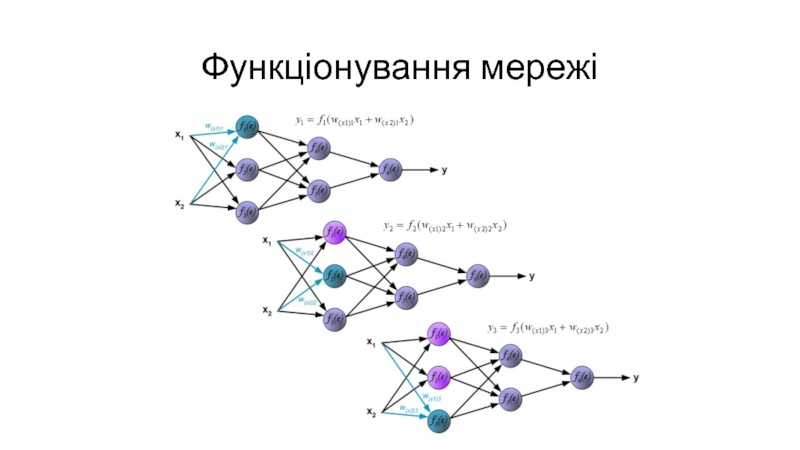
- 12. Функціонування мережі
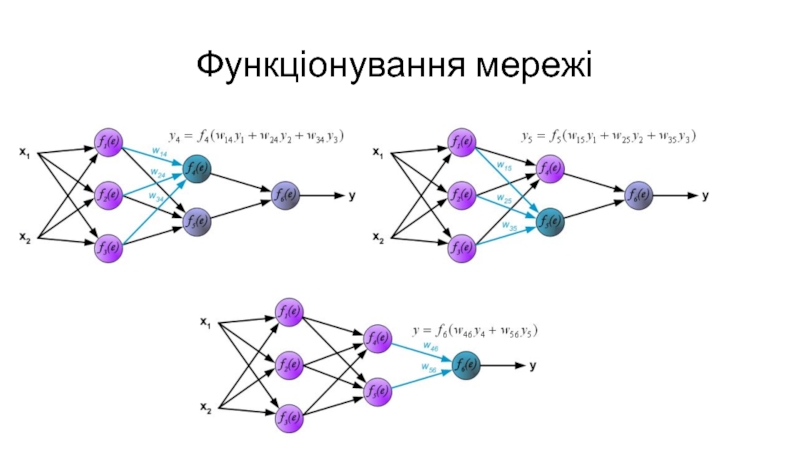
- 13. Функціонування мережі
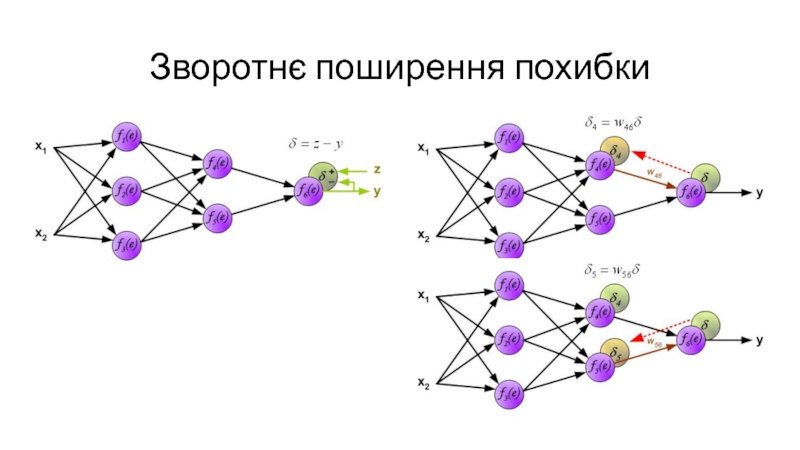
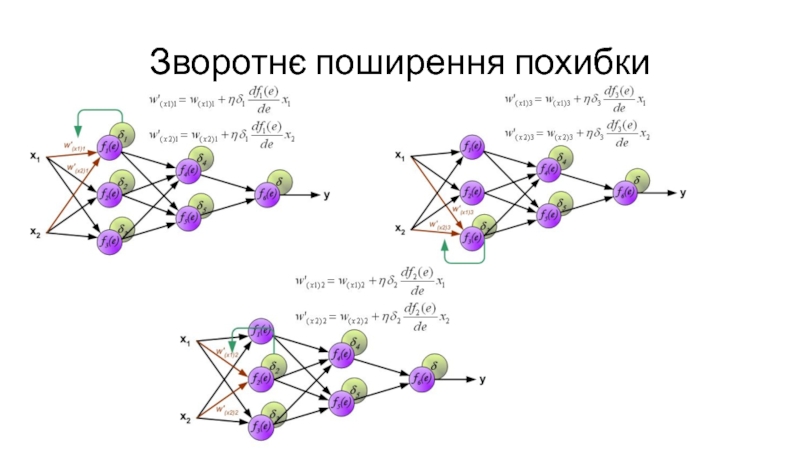
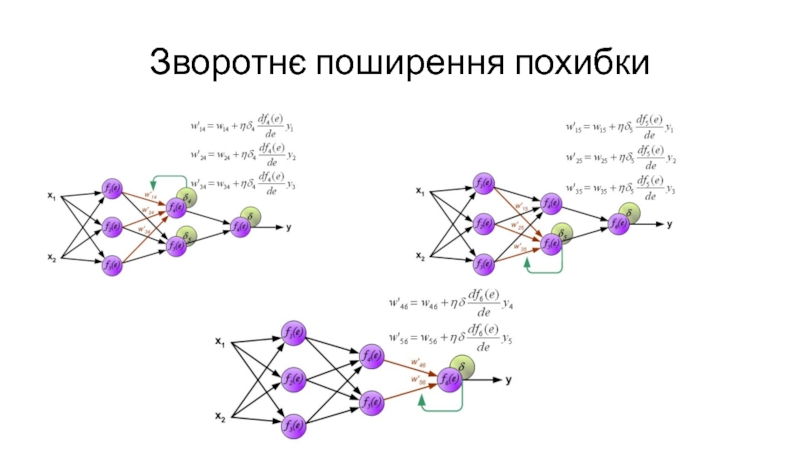
- 14. Зворотнє поширення похибки
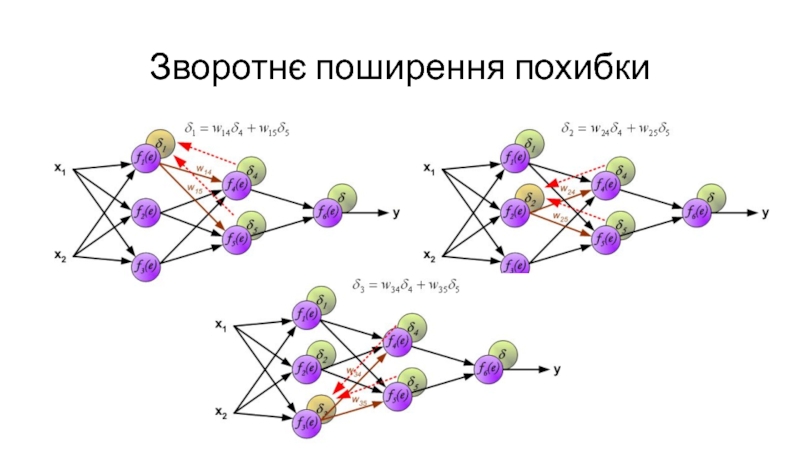
- 15. Зворотнє поширення похибки
- 16. Зворотнє поширення похибки
- 17. Зворотнє поширення похибки
- 18. Карти Кохонена (Self-Organizing Maps, SOM)Ідея мережі Кохонена належить фінскому вченому Тойво Кохонену (1982 рік)
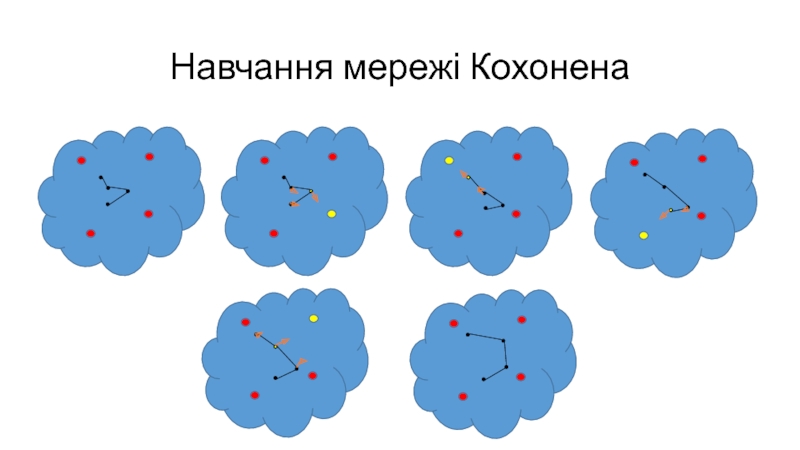
- 19. Навчання мережі Кохонена
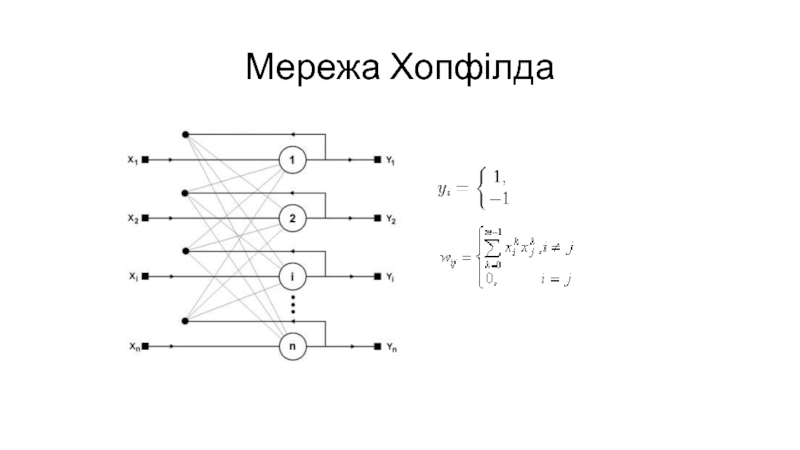
- 20. Мережа Хопфілда
- 21. Функціонування мережі ХопфілдаВстановити значення вхідного векторуРозрахувати
- 22. Мережа Хеммінга, i=0...n-1, k=0...m-1Tk = n / 2, k
- 23. Функціонування мережі ХеммінгаНа входи мережі надається незнайомий
- 24. РеалізаціяПрограмна з використанням матрицьПрограмна з використанням об’єктної моделіАпаратна на ПЛІС (FPGA)
- 25. Програмна з використанням матриць
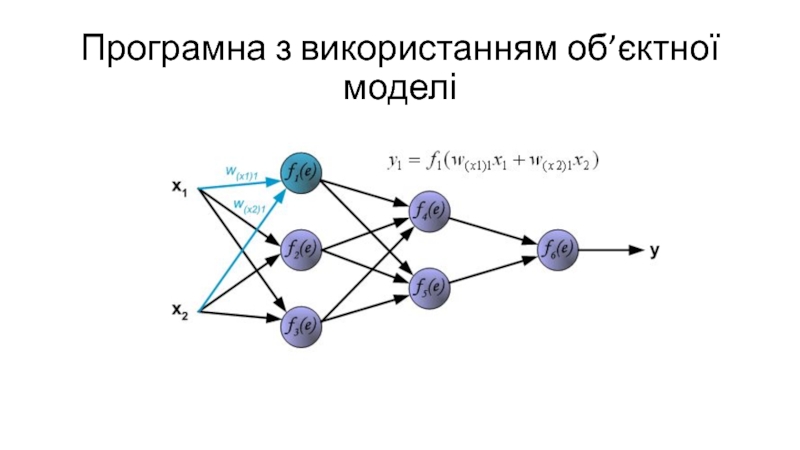
- 26. Програмна з використанням об’єктної моделі
- 27. Апаратна на ПЛІС (FPGA)
- 28. ЛітератураФ.Уоссермен, Нейрокомпьютерная техника, М.,Мир, 1992.Саймон Хайкин, Нейронные
- 29. Скачать презентанцию
Основні визначенняГіпотеза компактності: образам відповідають компактні множини у просторі ознакРозпізнавання образів — це віднессення данных до визначеного класу за допомогою признаків, що характеризують ці дані, з загальной маси даних
Слайды и текст этой презентации
Слайд 1Персептрони, дослідження в області нейронних мереж. Модель нейронної мережі зі
зворотним поширенням помилки.
Системи штучного інтелекту
Слайд 2Основні визначення
Гіпотеза компактності: образам відповідають компактні множини у просторі ознак
Розпізнавання
образів — це віднессення данных до визначеного класу за допомогою признаків,
що характеризують ці дані, з загальной маси данихСлайд 3Адаптація та навчання
Адаптація — це процес зміни параметрів та структури
системи, а можливо, й управляючих впливів на основі поточної інформації
з метою досягнення визначеного стану системи за умовами початковоъ невизначеносты та умовах функціонування, що змінюються.Навчання — це процес, завдяки якому система поступово набуває здатності відповідати потрібними реакціями на визначені сукупності звнішніх факторів.
Слайд 10Правила Хебба
Перше правило Хебба — Якщо сигнал перцептрона невірний та дорівнює
нулю, то необхідно збільшити вагові коефіцієнти тих входів, на які
було подано одиницю.Друге правило Хебба — Якщо сигнал перцептрона невірний та дорівнює одиниці, то необхідно зменьшити вагові коефіцієнти тих входів, на які було подано одиницю.
Правила застосовуються послідовно до всіх образів, що використовуються для навчання.
Слайд 18Карти Кохонена (Self-Organizing Maps, SOM)
Ідея мережі Кохонена належить фінскому вченому
Тойво Кохонену (1982 рік)
Слайд 21Функціонування мережі Хопфілда
Встановити значення вхідного вектору
Розрахувати
та
Чи змінились y, якщо так, то 2, інакше на виході маємо найбільш схожий образ
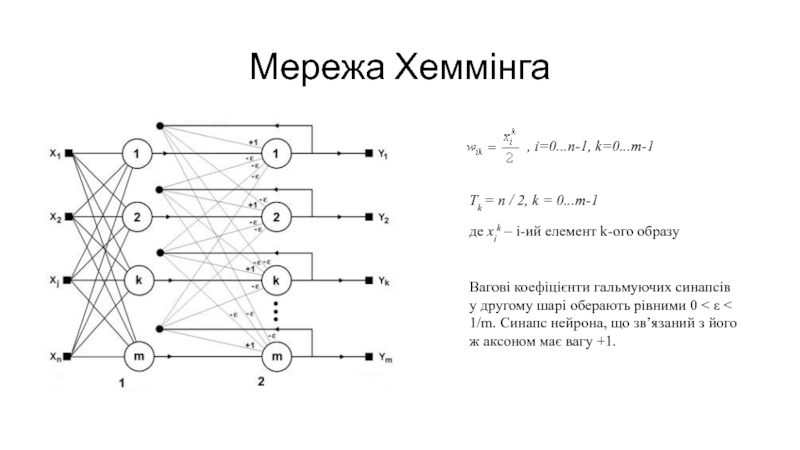
Слайд 22Мережа Хеммінга
, i=0...n-1, k=0...m-1
Tk = n / 2, k = 0...m-1
де xik – i-ий
елемент k-ого образу
Вагові коефіцієнти гальмуючих синапсів у другому шарі оберають
рівними 0 < e < 1/m. Синапс нейрона, що зв’язаний з його ж аксоном має вагу +1.Слайд 23Функціонування мережі Хеммінга
На входи мережі надається незнайомий вектор X = {xi:i=0...n-1}, виходячи
з якого розраховується стан нейронів першого шару (верхній індекс у
дужках вказує на номер шару):Після цього значеннями, що отримані ініціалізуються аксони другого шару: yj(2) = yj(1), j = 0...m-1
Обчислити нові стани нейронів другого шару:
та значення їх аксонів:
Функція активації f має вигляд порогу та F повинна бути достатньо великою, щоб будь які значення аргументу не призводили до насичення.
Перевірити, чи зменілись виходи нейронів другого слою за останню ітерацию. Якщо так – перейти до шагу 2. Інакше – завершення функціонування.
, j=0...m-1