Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ПИРАМИДА
Содержание
- 1. ПИРАМИДА
- 2. Термин “пирамида” заимствованиз греческого “пирамис” или “пирамидос”.
- 3. На окраине Каира - столицы современного Египта самая высокая - пирамида Хеопса
- 4. ОпределениеПирамида – многогранник, составленный из n -
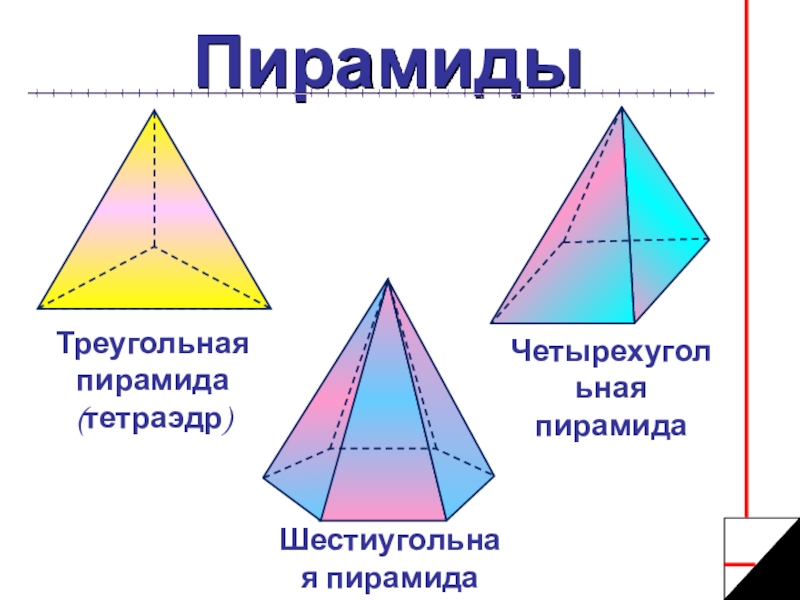
- 5. ПирамидыТреугольная пирамида (тетраэдр)Шестиугольная пирамидаЧетырехугольная пирамида
- 6. Пирамида называется правильной, если ее основание -
- 7. Апофема – высота боковой грани правильной пирамиды,
- 8. Принцип Кавальери —Если любая плоскость, параллельная данной, пересекает
- 9. Теорема: Объем пирамиды равен одной третьей произведения
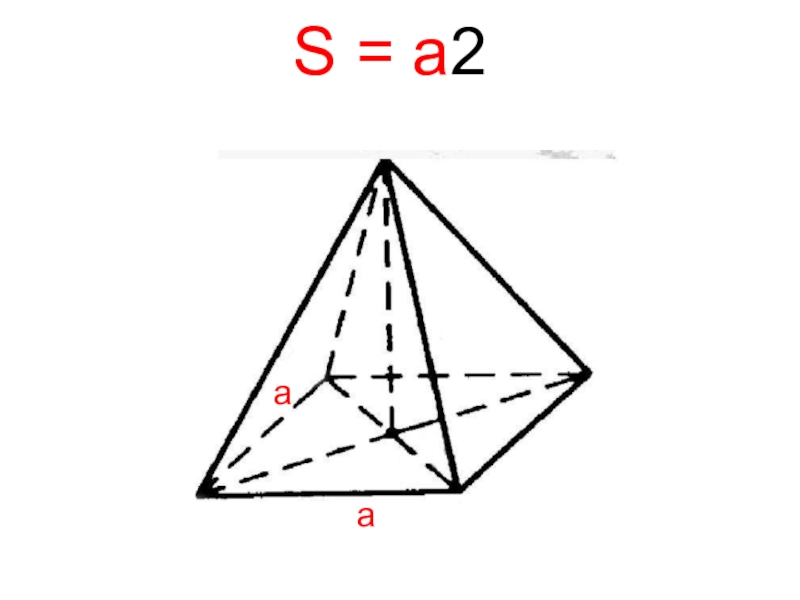
- 10. S = a2аа
- 11. Слайд 11
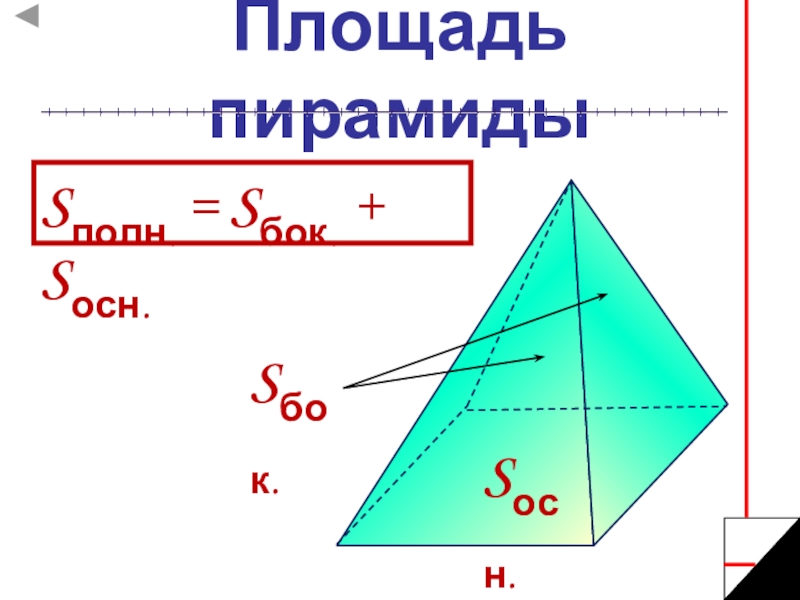
- 12. Площадь пирамидыSполн. = Sбок. + Sосн. Sбок.Sосн.
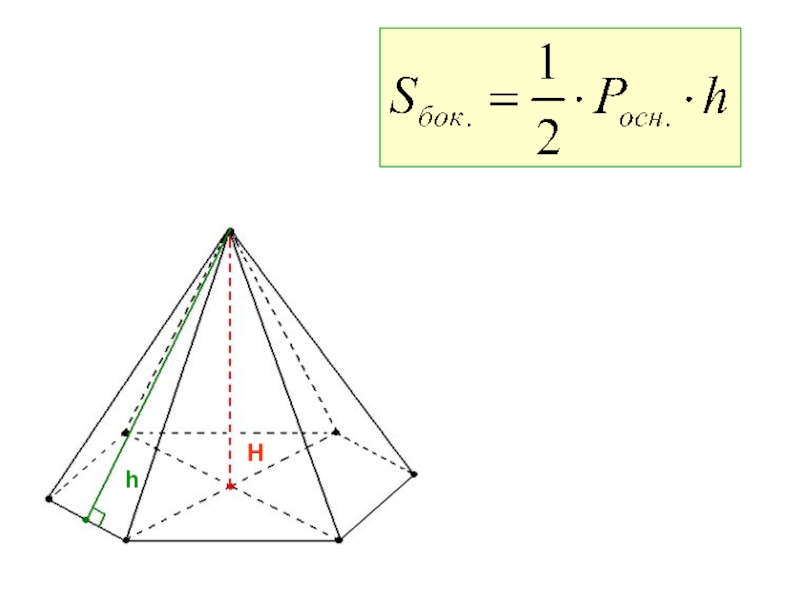
- 13. hH
- 14. Свойства пирамиды: У правильной пирамиды:
- 15. Слайд 15
- 16. Слайд 16
- 17. Скачать презентанцию
Термин “пирамида” заимствованиз греческого “пирамис” или “пирамидос”. Греки в свою очередь позаимствовали это слово, как полагают, из египетского языка. В папирусе Ахмеса встречается слово “пирамус” в смысле ребра правильной пирамиды. Другие
Слайды и текст этой презентации
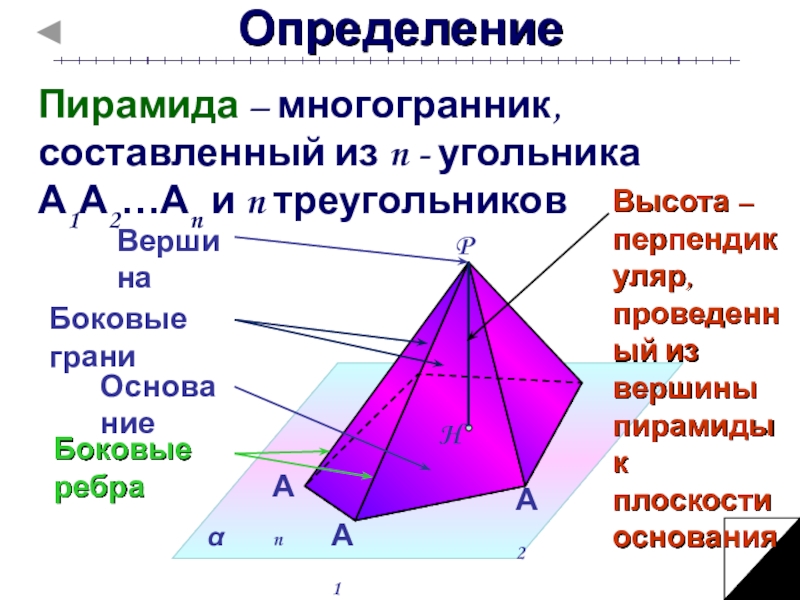
Слайд 4Определение
Пирамида – многогранник, составленный из n - угольника А1А2…Аn и
n треугольников
Высота – перпендикуляр, проведенный из вершины пирамиды к плоскости
основанияБоковые ребра
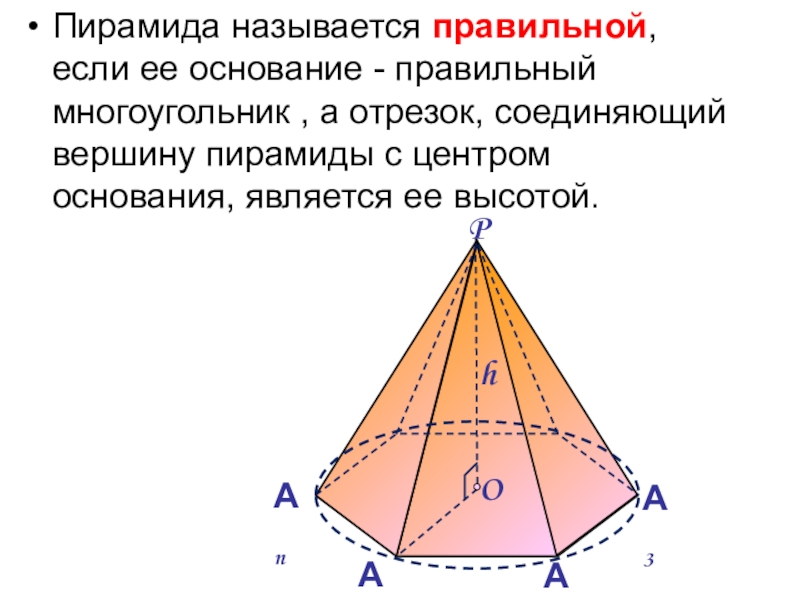
Слайд 6Пирамида называется правильной, если ее основание - правильный многоугольник ,
а отрезок, соединяющий вершину пирамиды с центром основания, является ее
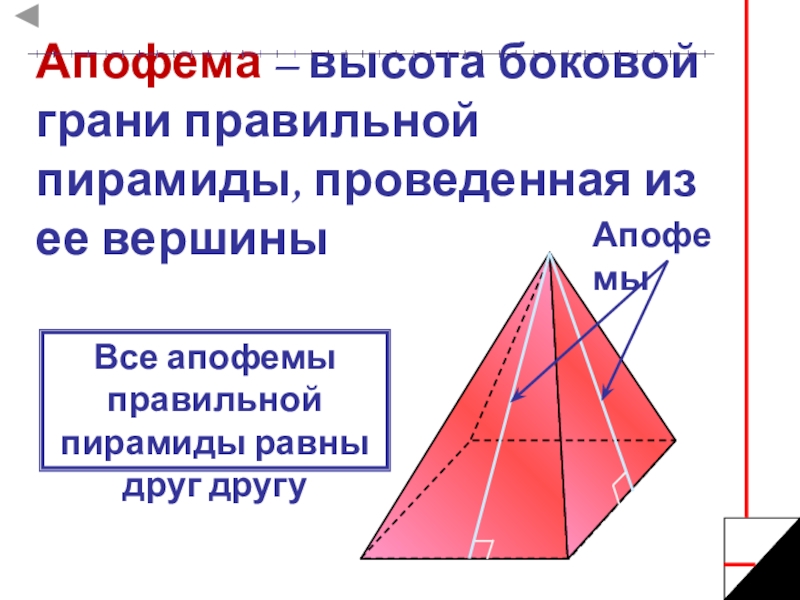
высотой.Слайд 7Апофема – высота боковой грани правильной пирамиды, проведенная из ее
вершины
Апофемы
Все апофемы правильной пирамиды равны друг другу
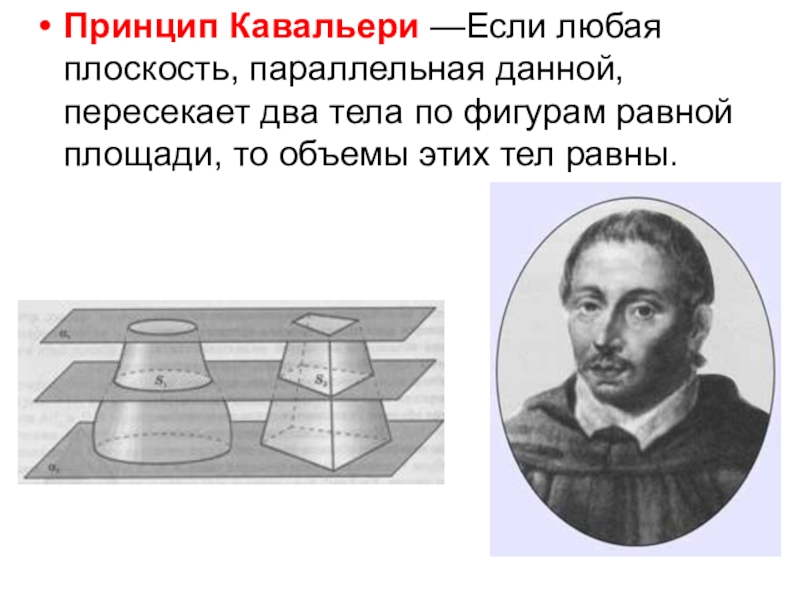
Слайд 8Принцип Кавальери —Если любая плоскость, параллельная данной, пересекает два тела по
фигурам равной площади, то объемы этих тел равны.
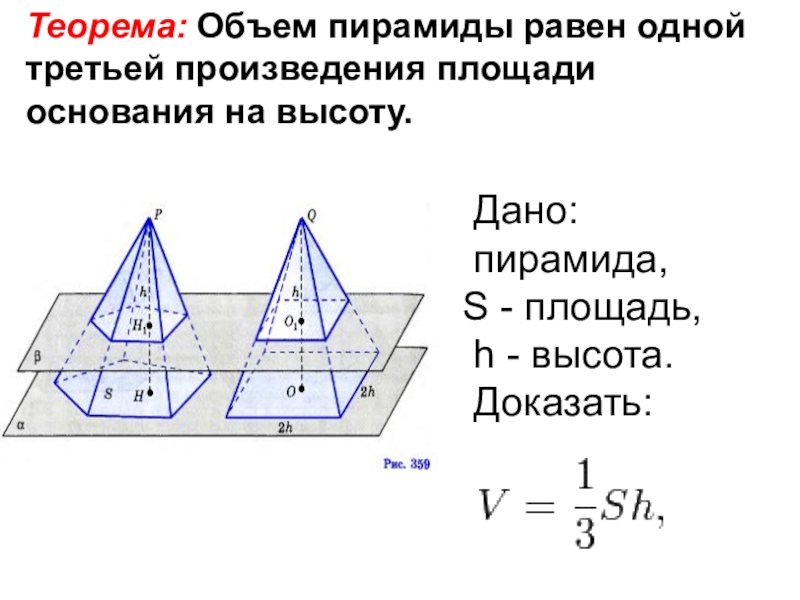
Слайд 9Теорема: Объем пирамиды равен одной третьей произведения площади основания на
высоту.
Дано:
пирамида,
S - площадь,
h - высота.
Доказать:
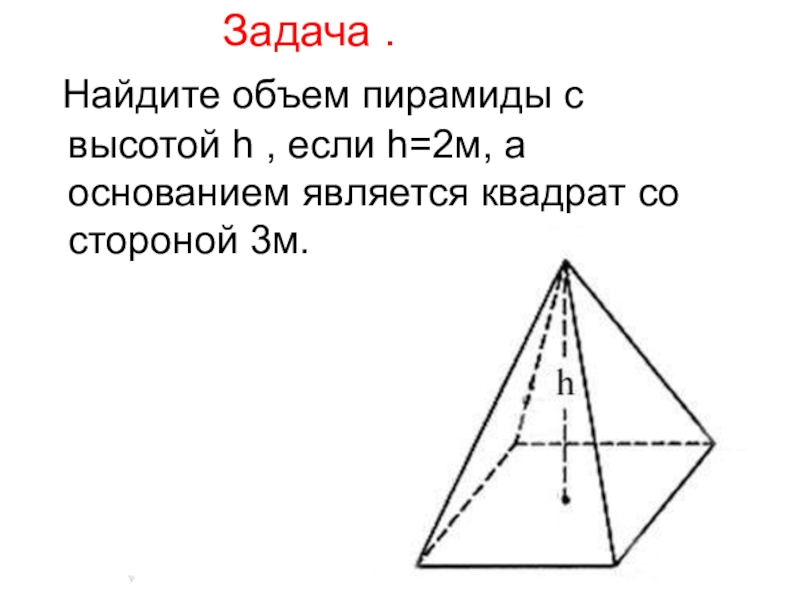
Слайд 11 Задача .
Найдите объем пирамиды с высотой h , если h=2м, а
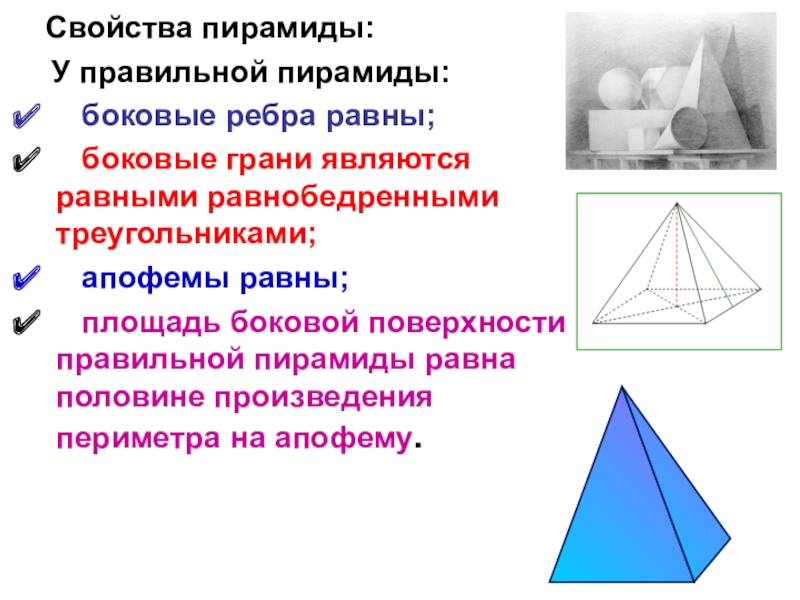
основанием является квадрат со стороной 3м.Слайд 14 Свойства пирамиды:
У правильной пирамиды:
боковые ребра
равны;
боковые грани являются равными равнобедренными треугольниками;
апофемы
равны;площадь боковой поверхности правильной пирамиды равна половине произведения периметра на апофему.