Плоские электромагнитные волны

и зарядов

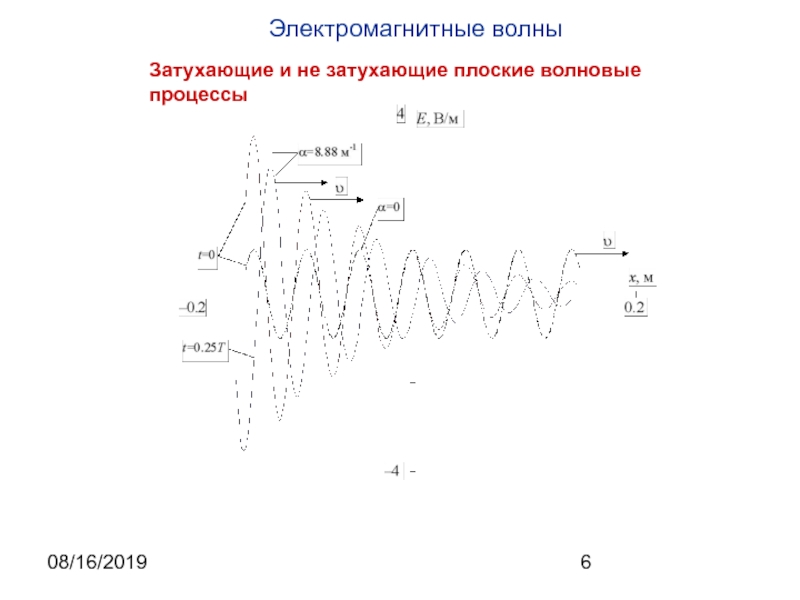
Из вида общего решения волнового уравнения, что плоская волна

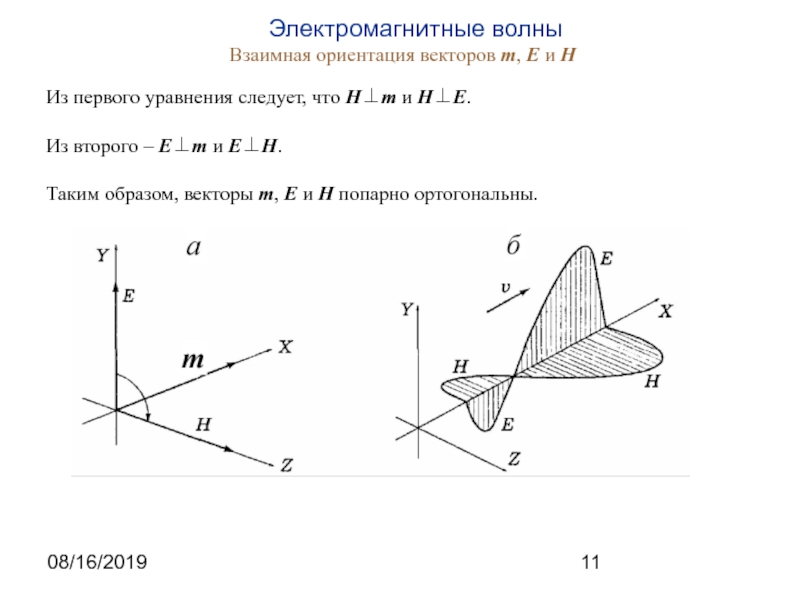
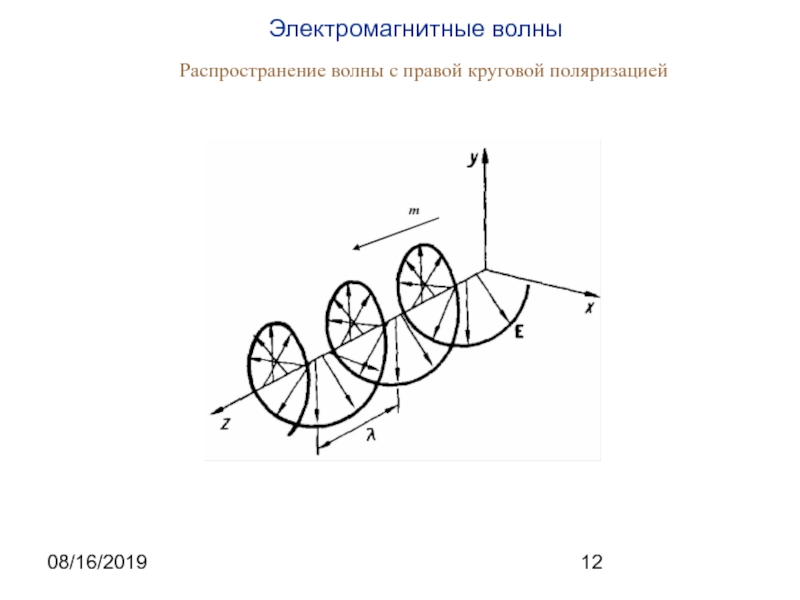
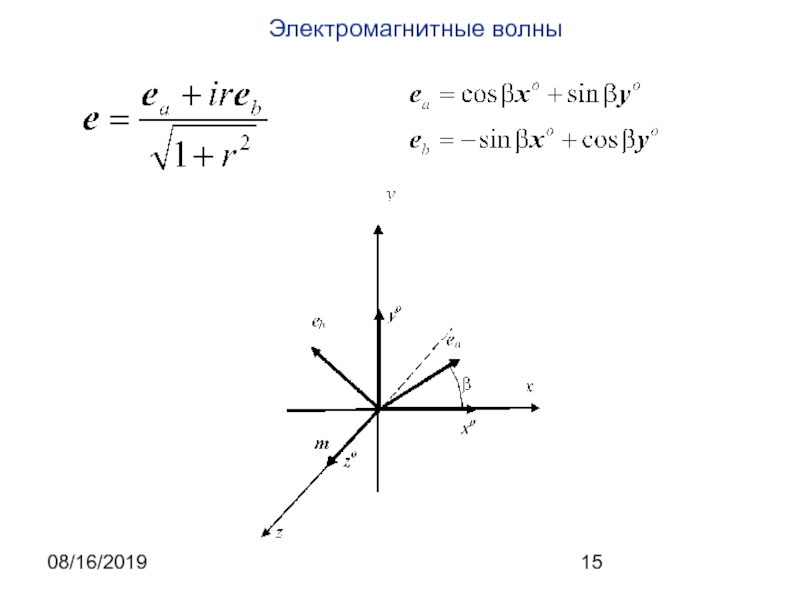
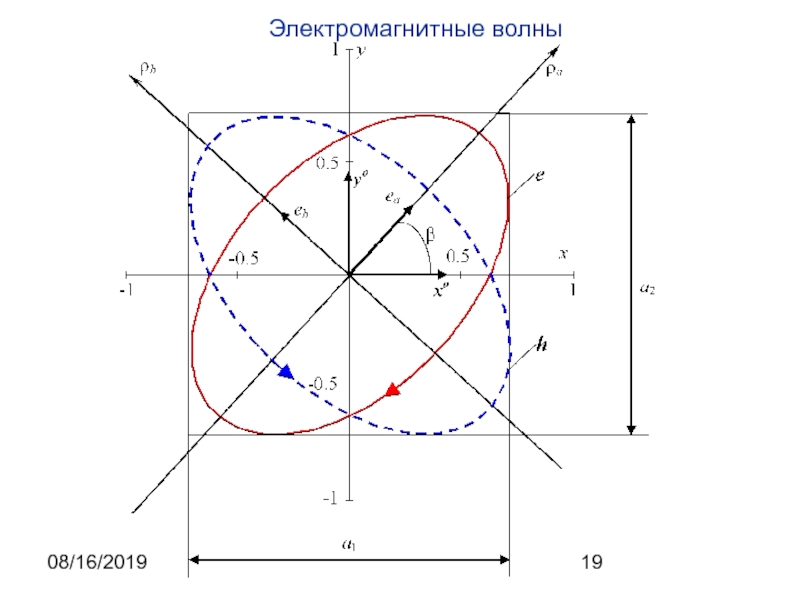
вида будет решением волнового уравнения волнового уравнения при σ=0. Следует отметить, что при записи плоской волны в этом виде конкретизируется только форма волнового фронта, а параметры волны, такие как частота ω и волновой вектор k остаются неизвестными. Они связаны с физическими параметрами среды распространения и могут быть определены при анализе математической модели волнового процесса. Примером такого определения является полученное выше соотношение, позволяющее вычислить величину волнового вектора и частоту через показатель преломления среды и волновое число в вакууме.
На практике обычно частота известна и требуется определить величину волнового вектора. В рассматриваемом случае направление волнового вектора в пространстве также считается заданным. Часто оно задается единичным вектором m (m⋅ m=m2=1). Тогда волновой вектор может быть представлен в форме , где скалярная величина k подлежит определению.

плоской волны при отличной от нуля проводимости σ≠0. Тогда подстановка

выражения для плоской волны в волновое уравнение преобразует его к виду

Для выполнения этого соотношения необходимо

Здесь введена величина тангенса угла диэлектрических потерь

m. Поскольку ориентация координатных осей ни чем не ограничена, то

можно считать, что волна распространяется вдоль положительного направления координатной оси Х. Тогда выражение для этой волны может быть преобразовано к виду

Пусть E+=E+yo=1(В/м)yo; f=1 мГц; μ=1; ε=10; σ=5⋅10-3 Ом-1⋅м-1.
Тогда ω=6.28⋅106 рад/с; n=3.162; tgδ=4.494⋅10-3; η=3.164; χ=0.106; α=8.88 м-1.

Распространение одной волны

Квадрат тангенса!!!!

В выражении, описывающем плоскую волны, распространяющуюся в положительном направлении оси

X они отрицательны. Для волны, распространяющейся в противоположном направлении, эти знаки будут положительными

следует, что H⊥m и H⊥E.

Из второго – E⊥m и

E⊥H.

Таким образом, векторы m, E и H попарно ортогональны.

в виде


Если

То фазы отнесем к комплексным амплитудам


Тогда
e⋅e*=1

и h⋅h*=1