Слайд 1ПЛОСКОПАРАЛЛЕЛЬНОЕ
ДВИЖЕНИЕ ТВЁРДОГО ТЕЛА
Кафедра теоретической механики и сопротивления материалов
Конспект лекции
Владивосток
2011
Составил В.
Г. Непейвода
ФЕДЕРАЛЬНОЕ АГЕНТСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
Морской государственный университет им. адм. Г. И. Невельского
Слайд 2Содержание
6. Определение ускорения точки плоской фигуры
1. Уравнения и характеристики плоскопараллельного
движения тела
2. Определение скорости точки плоской фигуры
3. Теорема о проекциях
скоростей двух точек плоской фигуры
4. Мгновенный центр скоростей
5. Определение положения мгновенного центра скоростей
Слайд 31. Уравнения и характеристики
плоскопараллельного движения тела
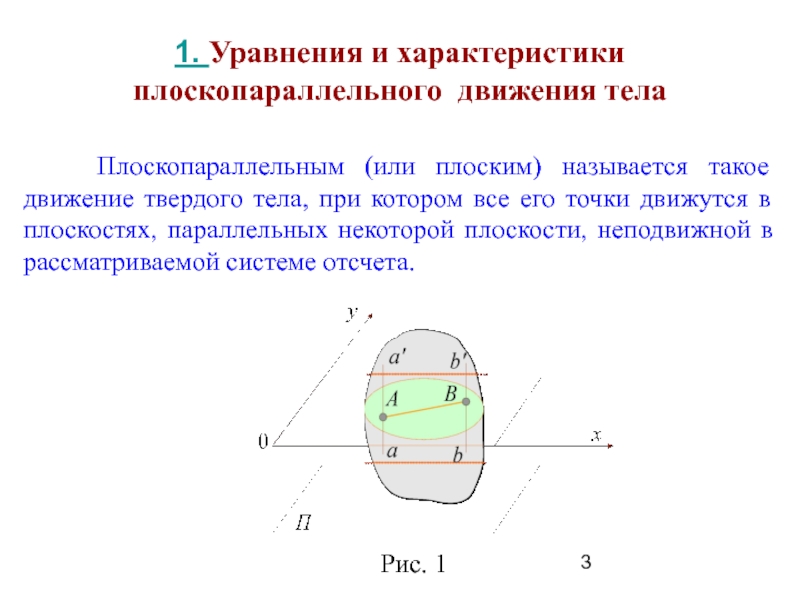
Плоскопараллельным
(или плоским) называется такое движение твердого тела, при котором все
его точки движутся в плоскостях, параллельных некоторой плоскости, неподвижной в рассматриваемой системе отсчета.
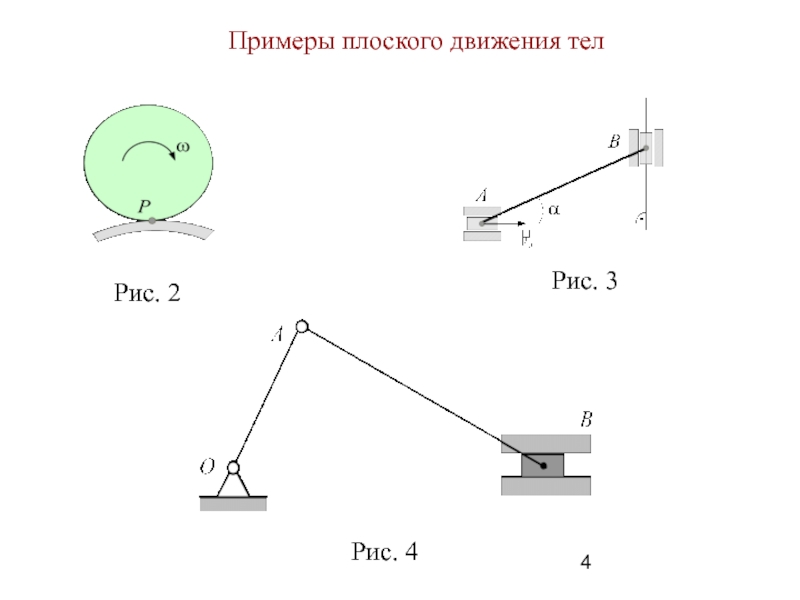
Слайд 4 Примеры плоского движения тел
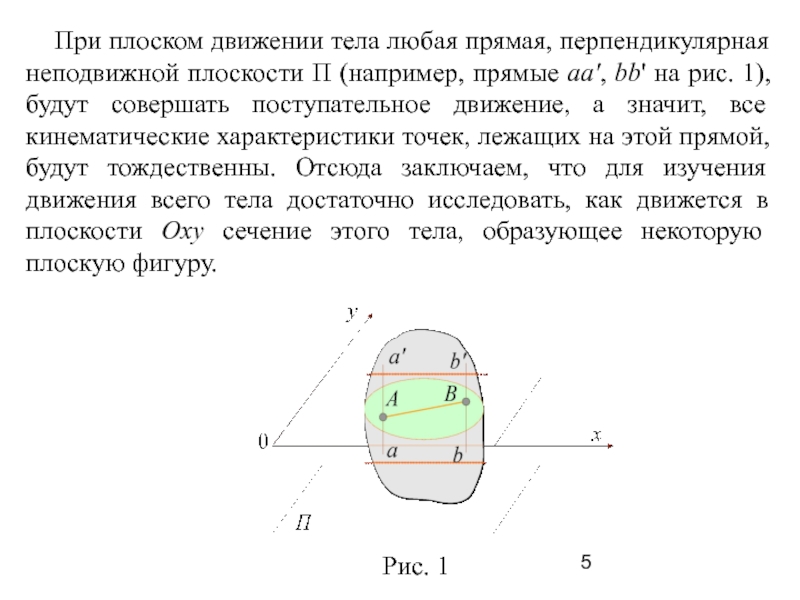
Слайд 5 При плоском движении тела любая прямая, перпендикулярная неподвижной
плоскости П (например, прямые аа', bb' на рис. 1), будут
совершать поступательное движение, а значит, все кинематические характеристики точек, лежащих на этой прямой, будут тождественны. Отсюда заключаем, что для изучения движения всего тела достаточно исследовать, как движется в плоскости Оху сечение этого тела, образующее некоторую плоскую фигуру.
Слайд 6 Положение плоской фигуры в плоскости Оху определяется положением
какого-либо проведенного на этой фигуре отрезка АВ (рис. 5). В
свою очередь, положение отрезка АВ определяется, например, координатами хA, уА точки А и величиной угла ϕ между отрезком АВ и осью х. Точку А, выбранную для определения положения плоской фигуры, называют полюсом.
Слайд 7 Таким образом, движение плоской фигуры в её плоскости,
а следовательно, и плоскопараллельного движения твердого тела относительно системы координат
Оху, определяется тремя уравнениями:
Слайд 8можно заключить, что движение плоской фигуры в ее плоскости представляет
собой совокупность двух движений: поступатель-ного движения, при котором все точки
движутся так же, как и полюс А, и вращательного движения вокруг этого полюса (при этом фигура вращается вокруг оси, проходящей через точку А перпендикулярно плоскости П).
Анализируя уравнения движения плоской фигуры,
Слайд 102. Определение скорости точки плоской фигуры
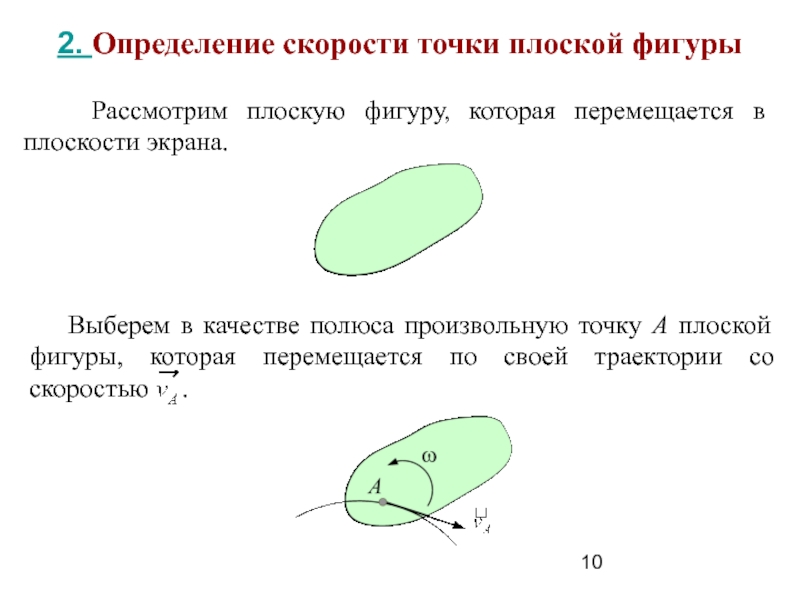
Рассмотрим плоскую
фигуру, которая перемещается в плоскости экрана.
Слайд 11 В предыдущем параграфе мы установили, что движение плоской
фигуры можно рассматривать как слагающееся из двух движений: поступательного движения
вместе с полюсом и вра-щательного движения вокруг полюса.
Определим скорость произвольной точки В.
Остановим вращательное движение плоской фигуры относительно полюса. В этом случае плоская фигура совершает поступательное движение и скорость точки В равна скорости точки А.
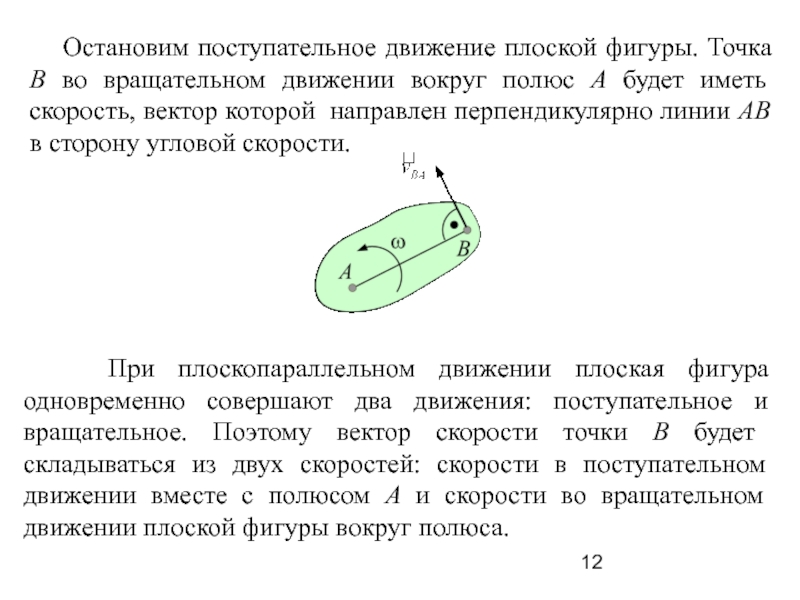
Слайд 12 Остановим поступательное движение плоской фигуры. Точка В во
вращательном движении вокруг полюс А будет иметь скорость, вектор которой
направлен перпендикулярно линии АВ в сторону угловой скорости.
При плоскопараллельном движении плоская фигура одновременно совершают два движения: поступательное и вращательное. Поэтому вектор скорости точки В будет складываться из двух скоростей: скорости в поступательном движении вместе с полюсом А и скорости во вращательном движении плоской фигуры вокруг полюса.
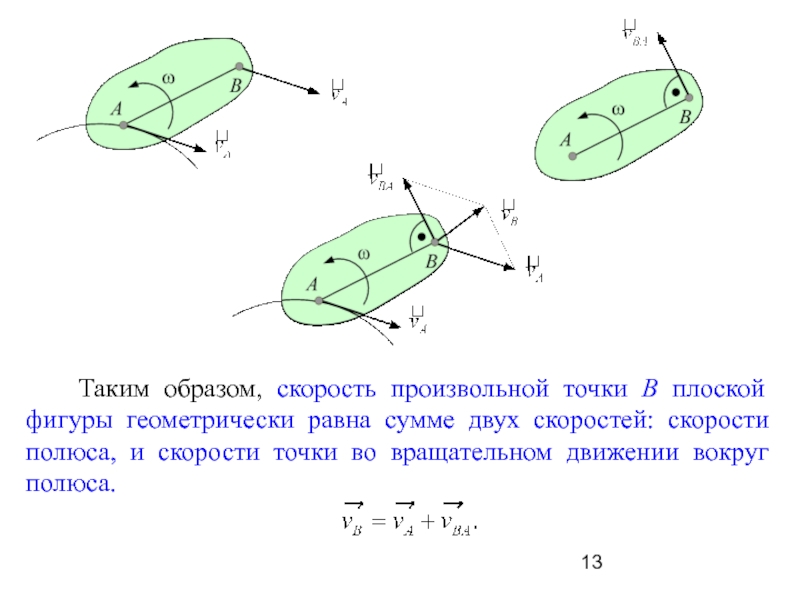
Слайд 13 Таким образом, скорость произвольной точки В плоской фигуры
геометрически равна сумме двух скоростей: скорости полюса, и скорости точки
во вращательном движении вокруг полюса.
Слайд 14 Приведенное векторное равенство получило название формулы Эйлера. В
соответствии с правилами векторной алгебры модуль скорости точки В равен:
Модуль скорости точки В можно определить, проецируя Формулу Эйлера на координатные оси:
Слайд 153. Теорема о проекциях скоростей двух точек плоской фигуры
Для двух произвольных точек плоской фигуры А и В справед-лива
формула Эйлера:
Рассмотрим движение плоской фигуры.
Слайд 16 Проведём через точки АВ ось x и спроецируем
на неё векторное выражение формулы Эйлера:
Слайд 17 Таким образом мы доказали теорему: проекции скоростей двух
произвольных точек плоской фигуры на ось, проведённую через эти точки,
равны.
Если углы, которые составляют векторы скоростей точек А и В с осью известны, то в соответствии с теоремой получим:
Слайд 184. Мгновенный центр скоростей
Из точки А построим перпендикуляр
к вектору скорости точки и отложим на нём отрезок АР,
равный:
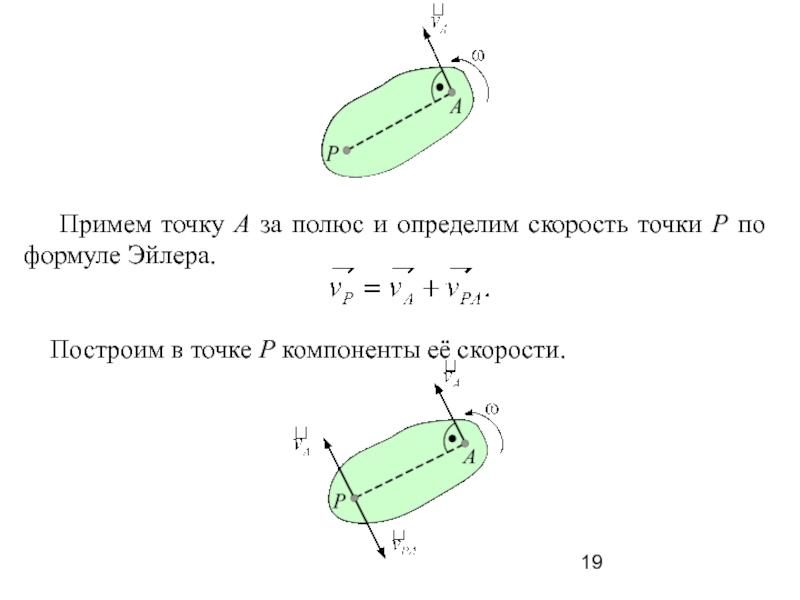
Слайд 19 Примем точку А за полюс и определим скорость
точки Р по формуле Эйлера.
Построим в точке Р
компоненты её скорости.
Слайд 20 Как видим, эти векторы имеют противоположное направ-ление.
Точка плоской фигуры, скорость которой в данный момент времени равна
нулю, называется мгновенным центром скоростей (МЦС).
Слайд 21 Мгновенный центр скоростей находится на перпендикуляре к вектору
скорости любой точки плоской фигуры и может быть расположен как
на самой фигуре так и за её пределами на её мысленном продолжении.
Слайд 225. Определение положения мгновенного
центра скоростей
Скорости точек равны:
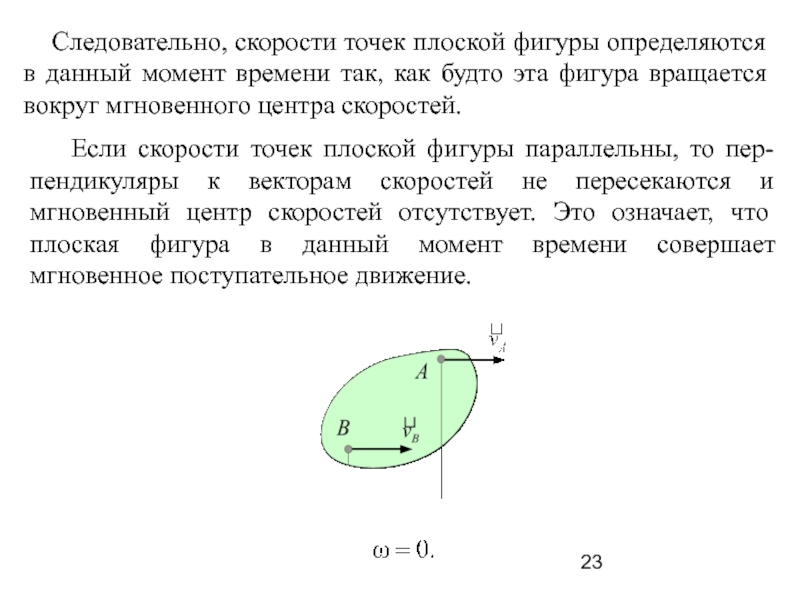
Слайд 23 Следовательно, скорости точек плоской фигуры определяются в данный
момент времени так, как будто эта фигура вращается вокруг мгновенного
центра скоростей.
Если скорости точек плоской фигуры параллельны, то пер-пендикуляры к векторам скоростей не пересекаются и мгновенный центр скоростей отсутствует. Это означает, что плоская фигура в данный момент времени совершает мгновенное поступательное движение.
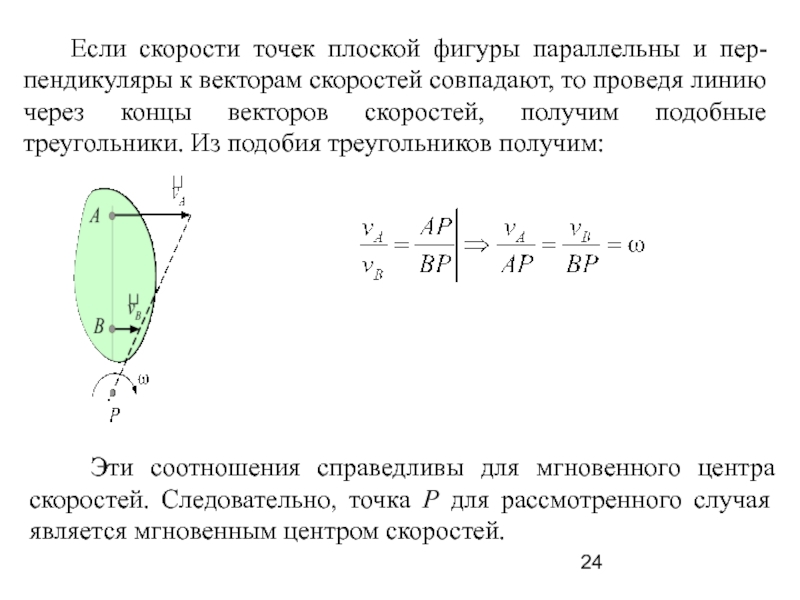
Слайд 24 Если скорости точек плоской фигуры параллельны и пер-пендикуляры
к векторам скоростей совпадают, то проведя линию через концы векторов
скоростей, получим подобные треугольники. Из подобия треугольников получим:
Эти соотношения справедливы для мгновенного центра скоростей. Следовательно, точка Р для рассмотренного случая является мгновенным центром скоростей.
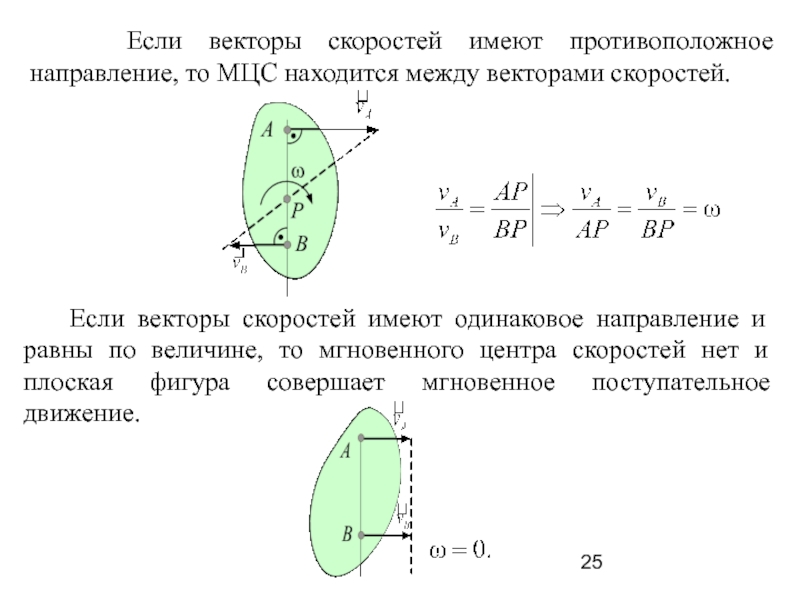
Слайд 25 Если векторы скоростей имеют противоположное направление, то МЦС
находится между векторами скоростей.
Если векторы скоростей имеют одинаковое
направление и равны по величине, то мгновенного центра скоростей нет и плоская фигура совершает мгновенное поступательное движение.
Слайд 266. Определение ускорения точки плоской фигуры
Рассмотрим плоскую фигуру.
Примем точку А за полюс и определим ускорение точки В.
При определении ускорения точки В так же будем исходить из того, что движение плоской фигуры состоит из двух движений: поступательного движения вместе с полюсом и вращательного вокруг полюса.
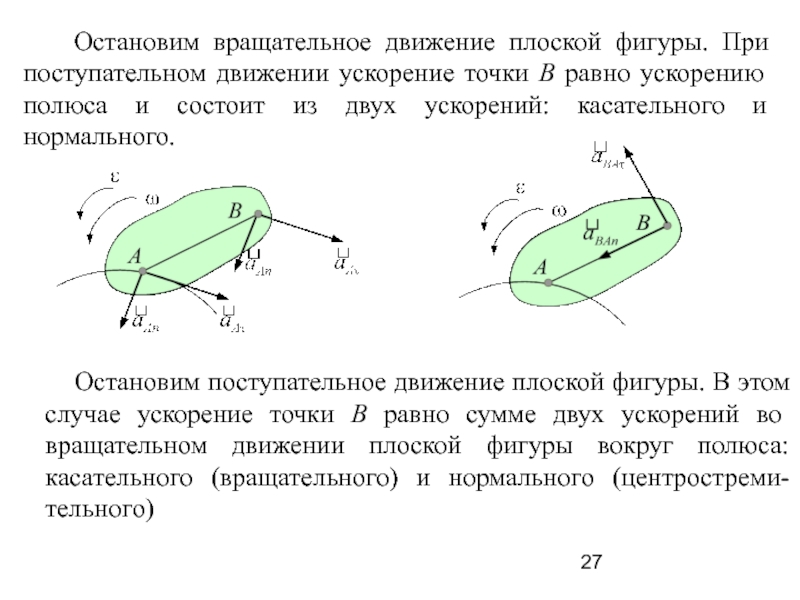
Слайд 27 Остановим вращательное движение плоской фигуры. При поступательном движении
ускорение точки В равно ускорению полюса и состоит из двух
ускорений: касательного и нормального.
Остановим поступательное движение плоской фигуры. В этом случае ускорение точки В равно сумме двух ускорений во вращательном движении плоской фигуры вокруг полюса: касательного (вращательного) и нормального (центростреми-тельного)
Слайд 28 Мы уже знаем, что при плоскопараллельном движении плоская
фигура одновременно совершают два движения: поступательное и вращательное. Поэтому вектор
ускорения точки В будет складываться из четырёх векторов: касательного и нормального ускорений точки в поступательном движении вместе с полюсом А и касательного и нормального ускорений точки во вращательном движении плоской фигуры вокруг полюса.
Слайд 29 Складывая векторы ускорений точки В в поступательном и
вращательном движениях плоской фигуры, получим:
Таким образом, ускорение произвольной
точки плоской фигуры равно сумме двух ускорений: ускорения полюса и ускорения точки во вращательном движении вокруг полюса.
Слайд 30 На практике при решении задач ускорение точки плоской
фигуры раскладывают на компоненты
а затем это векторное равенство проецируют
на координатные оси:
Если неизвестным является ускорение точки В, то находят модуль этого ускорения: