Пограничный слой

- ситуация очень малой вязкости, так что жидкость можно рассматривать

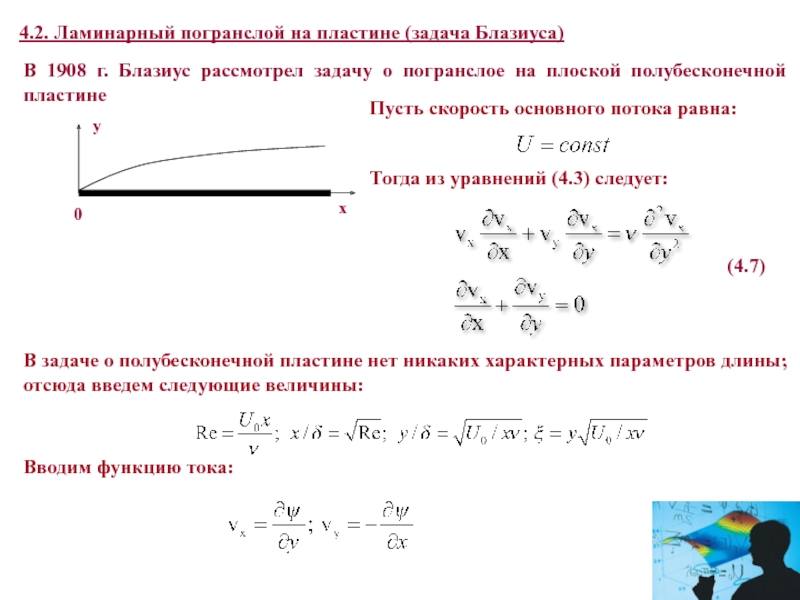
как идеальную. Однако, у идеальных жидкостей на твердых стенках - касательная компонента скорости отлична от нуля, а у вязких – равна нулю! Отсюда вывод: скорость до нуля вблизи твердых границ должна падать до нуля в очень тонком слое около тела. Такой слой носит название пограничного. Граница этого слоя не является, естественно, резкой и переход между погранслоем и внешним потоком жидкости непрерывен.
Рассмотрим систему уравнений, которыми описываются течения в тонком погранслое вблизи тела. Пусть имеет место двумерное обтекание жидкостью плоского участка поверхности тела (вдоль оси x). Тогда уравнения Навье-Стокса для стационарного течения имеют вид:

x

у

(4.1)

вязкости соизмеримы с силами инерции!

Прандтль
1875 — 1953гг.

- уравнения пограничного слоя Прандтля (1904г.)
Уравнения пограничного

слоя Прандтля (4.2) – незамкнуты: неизвестны компоненты скорости и давление; Прандтль предложил в первом приближении не учитывать обратного влияния погранслоя на внешний поток; поскольку толщина погранслоя мала, то распределение давления и скорости можно взять из внешнего (вне погранслоя) течения). Поскольку вне погранслоя течение потенциальное, то можно записать уравнение Бернулли:

(4.2)

x

у

Потенциальное течение

Окончательно получаем уравнения Прандтля в форме:

обтекании плоской стенки, но и в более сложных случаях геометрии

тел

Уравнения пограничного слоя Прандтля (1904г.)

Если ввести безразмерные переменные:

- скорость на бесконечности; тогда

(4.5)

Это означает, что решения этих уравнений не содержат числа Рейнольдса.

Таким образом, течение в пограничном слое при изменении числа Рейнольдса изменяется подобна сама себе: продольные расстояния и скорости остаются неизменными, а поперечные меняются обратно пропорционально корню из числа Рейнольдса!

Кроме того, нетрудно показать, что:

Отношение поперечной скорости к продольной обратно пропорционально !

При этом толщина погранслоя есть

(4.6)

рассмотрел задачу о погранслое на плоской полубесконечной пластине
x
y
0

Пусть скорость

основного потока равна:

В задаче о полубесконечной пластине нет никаких характерных параметров длины; отсюда введем следующие величины:

Тогда из уравнений (4.3) следует:

(4.7)

Вводим функцию тока:

получить только численно.
0.4
0.8
1.0

5.0
4.0
3.0
2.0
1.0
0

Толщина погранслоя
За толщину погранслоя принимают следующее условие
y
0

x

Или
(4.10)
Таким

образом, вблизи начала пластины решение Блазиуса несправедливо – имеется

Средний коэффициент сопротивления трения:
Пределы применимости решения Блазиуса:
Оценки: