Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ 1 Эта последовательность вводит полулогарифмическую
Содержание
- 1. ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ 1 Эта последовательность вводит полулогарифмическую
- 2. 2Дифференциал Y по X упрощается до b2Y.ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
- 3. 3Следовательно, пропорциональное изменение Y на единицу изменения
- 4. 4ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
- 5. 5Предположим, что X увеличивается на величину DX и, как следствие, Y увеличивается на величину DY.ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
- 6. 6 Мы можем переписать правую часть уравнения, как показано.ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
- 7. 7Мы можем упростить правую часть уравнения, как показано.ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
- 8. 8Теперь разложим показательную функцию, используя стандартное выражение для е до некоторой степени.ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
- 9. 9Вычитаем Y с обеих сторон.ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
- 10. 10Рассмотрим теперь два случая: где b2 и
- 11. 11Если (b2 DX)2 пренебрежимо мало, мы получаем ту же интерпретацию b2 что и следовало ожидать.ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИnegligible
- 12. 12ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИЕсли (b2 DX)2 не является пренебрежимо
- 13. 13Обычно мы говорим о влиянии изменения одной
- 14. 14b1 является значением Y когда X равно нулю (заметим, что e0 равно 1).ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
- 15. 15Чтобы соответствовать функции этого типа, вы берете
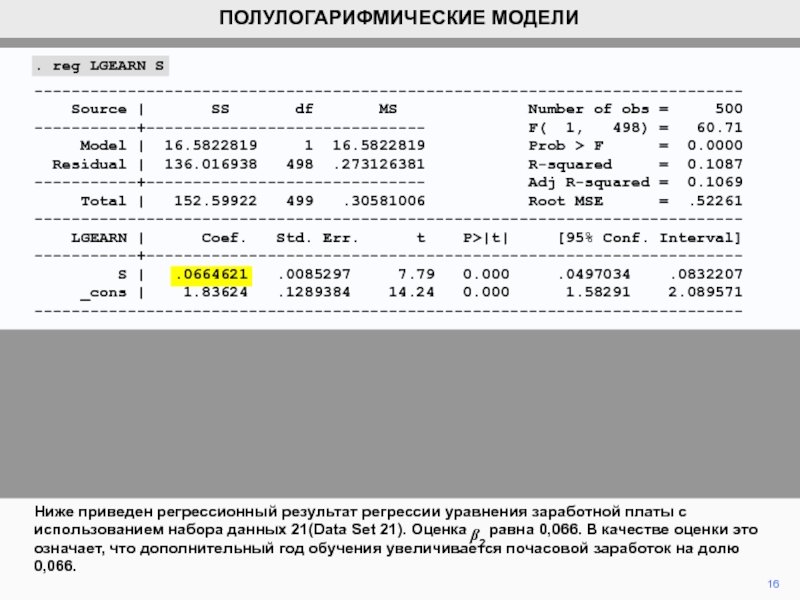
- 16. Ниже приведен регрессионный результат регрессии уравнения заработной
- 17. В повседневном языке более естественно говорить о
- 18. Если учесть тот факт, что год
- 19. 19В общем случае, если единичное изменение в
- 20. 20Однако, если изменение единицы в X не
- 21. 21В общем случае, когда b2 меньше 0.1,
- 22. Константа в регрессии представляет собой возможное значение
- 23. 23В буквальном смысле это означает, что человек
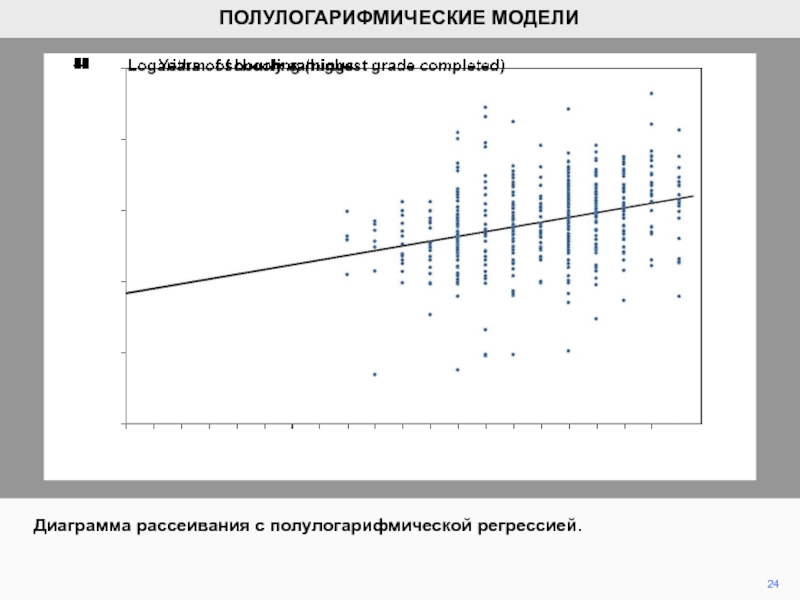
- 24. Диаграмма рассеивания с полулогарифмической регрессией.24ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
- 25. Полулогарифмическая линия регрессии, построенная на диаграмме рассеивания
- 26. 26 Нет большой разницы в подходе регрессионных
- 27. 27Линейная спецификация предсказывает, что ежечасная заработная плата
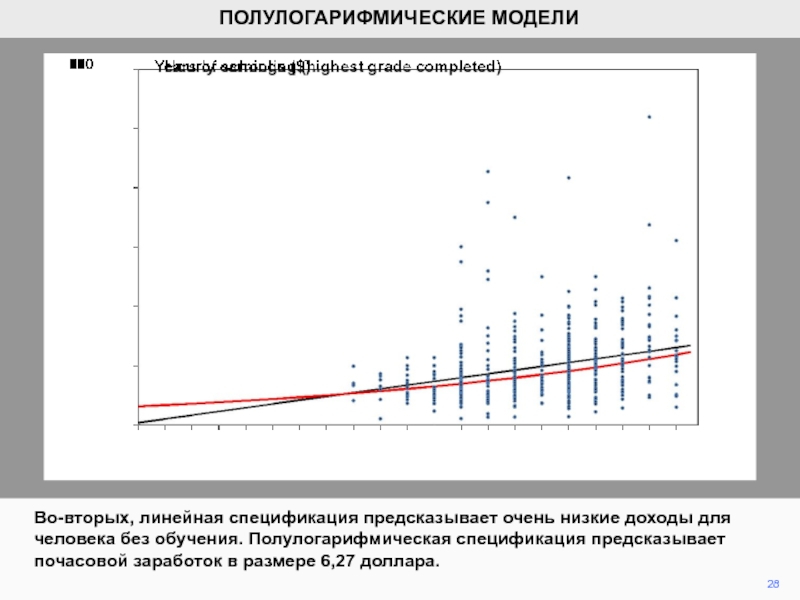
- 28. 28Во-вторых, линейная спецификация предсказывает очень низкие доходы
- 29. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
1
Эта последовательность вводит полулогарифмическую модель и показывает, как она
Слайд 33
Следовательно, пропорциональное изменение Y на единицу изменения в X равно
b2. Поэтому он не зависит от значения X.
ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
Слайд 55
Предположим, что X увеличивается на величину DX и, как следствие,
Y увеличивается на величину DY.
ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
Слайд 88
Теперь разложим показательную функцию, используя стандартное выражение для е до
некоторой степени.
ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
Слайд 1010
Рассмотрим теперь два случая: где b2 и DX настолько малы,
что (b2 DX)2 пренебрежимо мало, и альтернативно.
ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
negligible
Слайд 1111
Если (b2 DX)2 пренебрежимо мало, мы получаем ту же интерпретацию
b2 что и следовало ожидать.
ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
negligible
Слайд 1212
ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
Если (b2 DX)2 не является пренебрежимо малым, пропорциональное изменение
в Y при изменении DX в X имеет дополнительный член
(Предположим, что b2 и DX достаточно малы, что с более высокими степенями DX можно пренебречь.)not negligible
Слайд 1313
Обычно мы говорим о влиянии изменения одной части переменной X.
Если DX = 1, пропорциональное изменение происходит в Y ,
как показано. Теперь значение b2 становится настолько малым, что вторым и последующим значениями можно пренебречь.if DX is one unit
ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
not negligible
Слайд 1414
b1 является значением Y когда X равно нулю (заметим, что
e0 равно 1).
ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
Слайд 1515
Чтобы соответствовать функции этого типа, вы берете логарифмы с обеих
сторон. Правая часть уравнения становится линейной функцией от X (заметим,
что логарифм e на основание e равен 1). Следовательно, мы можем поместить модель с линейной регрессией log Y на X.ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
Слайд 16Ниже приведен регрессионный результат регрессии уравнения заработной платы с использованием
набора данных 21(Data Set 21). Оценка равна 0,066.
В качестве оценки это означает, что дополнительный год обучения увеличивается почасовой заработок на долю 0,066.16
ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
. reg LGEARN S
----------------------------------------------------------------------------
Source | SS df MS Number of obs = 500
-----------+------------------------------ F( 1, 498) = 60.71
Model | 16.5822819 1 16.5822819 Prob > F = 0.0000
Residual | 136.016938 498 .273126381 R-squared = 0.1087
-----------+------------------------------ Adj R-squared = 0.1069
Total | 152.59922 499 .30581006 Root MSE = .52261
----------------------------------------------------------------------------
LGEARN | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
S | .0664621 .0085297 7.79 0.000 .0497034 .0832207
_cons | 1.83624 .1289384 14.24 0.000 1.58291 2.089571
----------------------------------------------------------------------------
b2
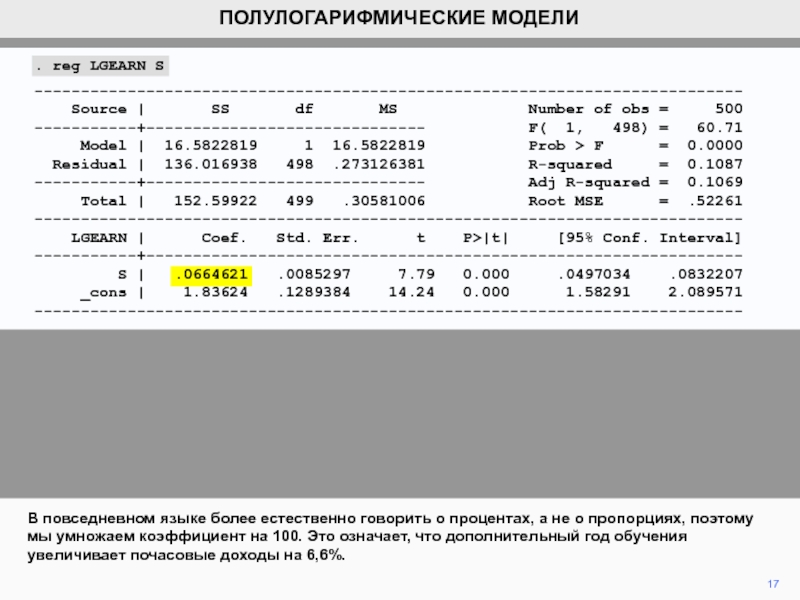
Слайд 17В повседневном языке более естественно говорить о процентах, а не
о пропорциях, поэтому мы умножаем коэффициент на 100. Это означает,
что дополнительный год обучения увеличивает почасовые доходы на 6,6%.17
ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
. reg LGEARN S
----------------------------------------------------------------------------
Source | SS df MS Number of obs = 500
-----------+------------------------------ F( 1, 498) = 60.71
Model | 16.5822819 1 16.5822819 Prob > F = 0.0000
Residual | 136.016938 498 .273126381 R-squared = 0.1087
-----------+------------------------------ Adj R-squared = 0.1069
Total | 152.59922 499 .30581006 Root MSE = .52261
----------------------------------------------------------------------------
LGEARN | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
S | .0664621 .0085297 7.79 0.000 .0497034 .0832207
_cons | 1.83624 .1289384 14.24 0.000 1.58291 2.089571
----------------------------------------------------------------------------
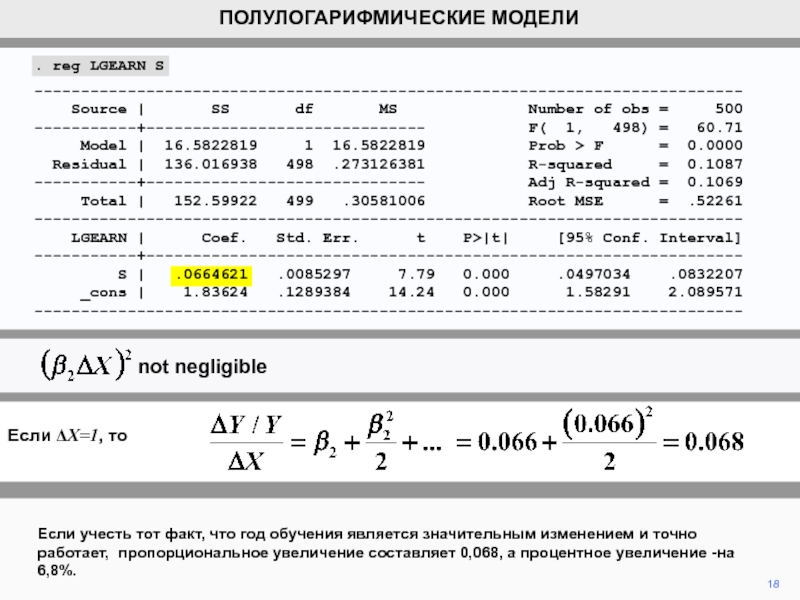
Слайд 18 Если учесть тот факт, что год обучения является значительным изменением
и точно работает, пропорциональное увеличение составляет 0,068, а процентное увеличение
-на 6,8%.18
ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
. reg LGEARN S
----------------------------------------------------------------------------
Source | SS df MS Number of obs = 500
-----------+------------------------------ F( 1, 498) = 60.71
Model | 16.5822819 1 16.5822819 Prob > F = 0.0000
Residual | 136.016938 498 .273126381 R-squared = 0.1087
-----------+------------------------------ Adj R-squared = 0.1069
Total | 152.59922 499 .30581006 Root MSE = .52261
----------------------------------------------------------------------------
LGEARN | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
S | .0664621 .0085297 7.79 0.000 .0497034 .0832207
_cons | 1.83624 .1289384 14.24 0.000 1.58291 2.089571
----------------------------------------------------------------------------
Если DX=1, то
not negligible
Слайд 1919
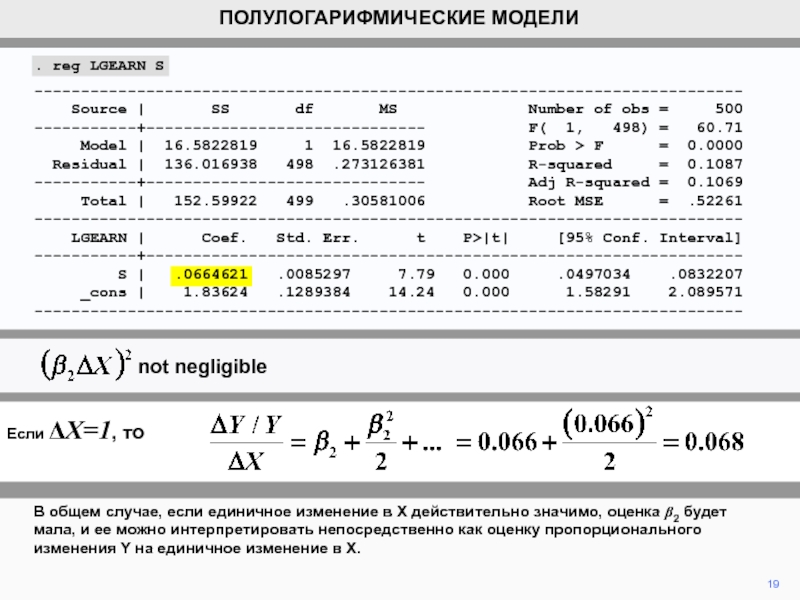
В общем случае, если единичное изменение в X действительно значимо,
оценка b2 будет мала, и ее можно интерпретировать непосредственно как
оценку пропорционального изменения Y на единичное изменение в X.ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
. reg LGEARN S
----------------------------------------------------------------------------
Source | SS df MS Number of obs = 500
-----------+------------------------------ F( 1, 498) = 60.71
Model | 16.5822819 1 16.5822819 Prob > F = 0.0000
Residual | 136.016938 498 .273126381 R-squared = 0.1087
-----------+------------------------------ Adj R-squared = 0.1069
Total | 152.59922 499 .30581006 Root MSE = .52261
----------------------------------------------------------------------------
LGEARN | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
S | .0664621 .0085297 7.79 0.000 .0497034 .0832207
_cons | 1.83624 .1289384 14.24 0.000 1.58291 2.089571
----------------------------------------------------------------------------
Если DX=1, то
not negligible
Слайд 2020
Однако, если изменение единицы в X не мало, коэффициент может
быть большим, а второй член может быть незначительным. В данном
случае год обучения не является значительным, но ясно, что уточнение делает лишь небольшую разницу.ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
. reg LGEARN S
----------------------------------------------------------------------------
Source | SS df MS Number of obs = 500
-----------+------------------------------ F( 1, 498) = 60.71
Model | 16.5822819 1 16.5822819 Prob > F = 0.0000
Residual | 136.016938 498 .273126381 R-squared = 0.1087
-----------+------------------------------ Adj R-squared = 0.1069
Total | 152.59922 499 .30581006 Root MSE = .52261
----------------------------------------------------------------------------
LGEARN | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
S | .0664621 .0085297 7.79 0.000 .0497034 .0832207
_cons | 1.83624 .1289384 14.24 0.000 1.58291 2.089571
----------------------------------------------------------------------------
Если DX=1, то
not negligible
Слайд 2121
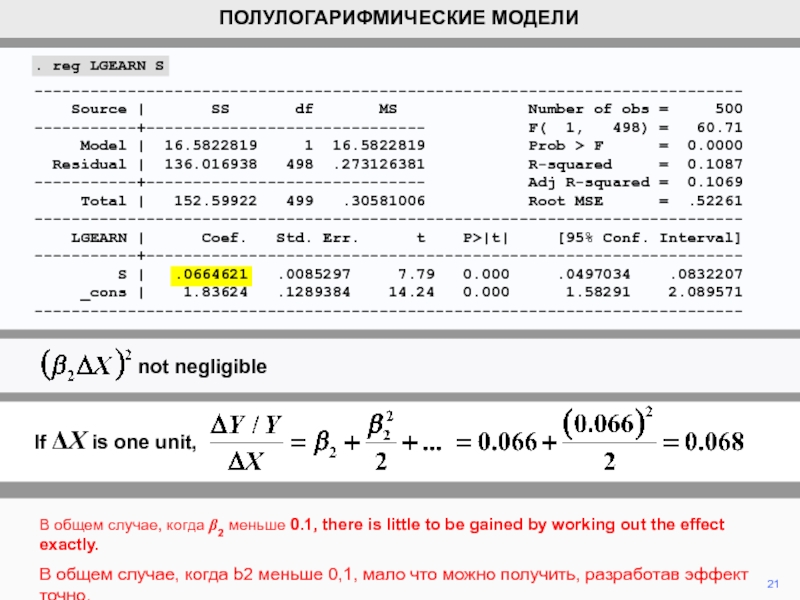
В общем случае, когда b2 меньше 0.1, there is little
to be gained by working out the effect exactly.
В общем
случае, когда b2 меньше 0,1, мало что можно получить, разработав эффект точно.ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
. reg LGEARN S
----------------------------------------------------------------------------
Source | SS df MS Number of obs = 500
-----------+------------------------------ F( 1, 498) = 60.71
Model | 16.5822819 1 16.5822819 Prob > F = 0.0000
Residual | 136.016938 498 .273126381 R-squared = 0.1087
-----------+------------------------------ Adj R-squared = 0.1069
Total | 152.59922 499 .30581006 Root MSE = .52261
----------------------------------------------------------------------------
LGEARN | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
S | .0664621 .0085297 7.79 0.000 .0497034 .0832207
_cons | 1.83624 .1289384 14.24 0.000 1.58291 2.089571
----------------------------------------------------------------------------
If DX is one unit,
not negligible
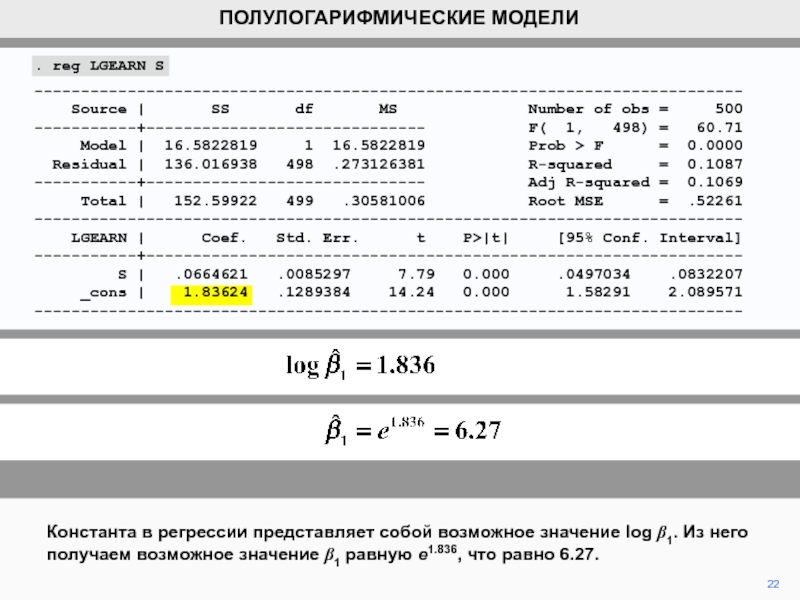
Слайд 22Константа в регрессии представляет собой возможное значение log b1. Из
него получаем возможное значение b1 равную e1.836, что равно 6.27.
22
ПОЛУЛОГАРИФМИЧЕСКИЕ
МОДЕЛИ. reg LGEARN S
Source | SS df MS Number of obs = 540
-------------+------------------------------ F( 1, 538) = 140.05
Model | 38.5643833 1 38.5643833 Prob > F = 0.0000
Residual | 148.14326 538 .275359219 R-squared = 0.2065
-------------+------------------------------ Adj R-squared = 0.2051
Total | 186.707643 539 .34639637 Root MSE = .52475
------------------------------------------------------------------------------
LGEARN | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
S | .1096934 .0092691 11.83 0.000 .0914853 .1279014
_cons | 1.292241 .1287252 10.04 0.000 1.039376 1.545107
------------------------------------------------------------------------------
. reg LGEARN S
----------------------------------------------------------------------------
Source | SS df MS Number of obs = 500
-----------+------------------------------ F( 1, 498) = 60.71
Model | 16.5822819 1 16.5822819 Prob > F = 0.0000
Residual | 136.016938 498 .273126381 R-squared = 0.1087
-----------+------------------------------ Adj R-squared = 0.1069
Total | 152.59922 499 .30581006 Root MSE = .52261
----------------------------------------------------------------------------
LGEARN | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
S | .0664621 .0085297 7.79 0.000 .0497034 .0832207
_cons | 1.83624 .1289384 14.24 0.000 1.58291 2.089571
----------------------------------------------------------------------------
Слайд 2323
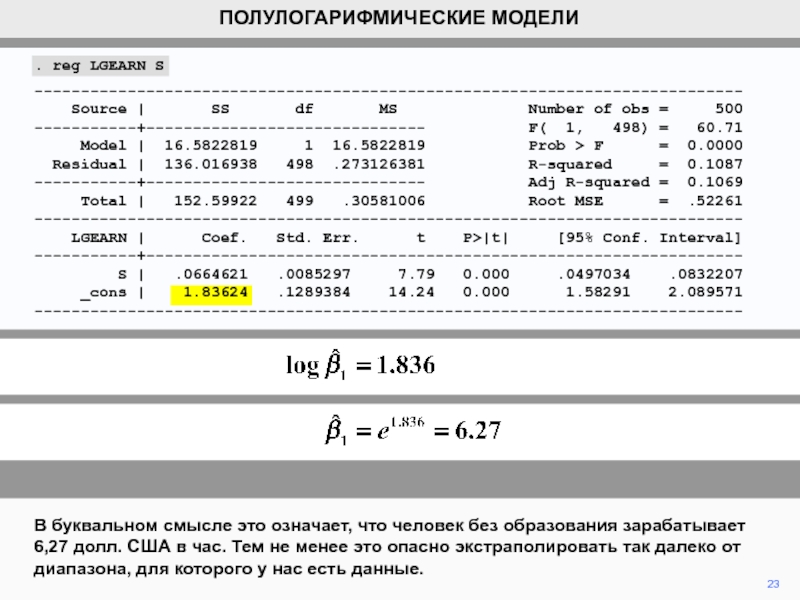
В буквальном смысле это означает, что человек без образования зарабатывает
6,27 долл. США в час. Тем не менее это опасно
экстраполировать так далеко от диапазона, для которого у нас есть данные.ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
. reg LGEARN S
Source | SS df MS Number of obs = 540
-------------+------------------------------ F( 1, 538) = 140.05
Model | 38.5643833 1 38.5643833 Prob > F = 0.0000
Residual | 148.14326 538 .275359219 R-squared = 0.2065
-------------+------------------------------ Adj R-squared = 0.2051
Total | 186.707643 539 .34639637 Root MSE = .52475
------------------------------------------------------------------------------
LGEARN | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
S | .1096934 .0092691 11.83 0.000 .0914853 .1279014
_cons | 1.292241 .1287252 10.04 0.000 1.039376 1.545107
------------------------------------------------------------------------------
. reg LGEARN S
----------------------------------------------------------------------------
Source | SS df MS Number of obs = 500
-----------+------------------------------ F( 1, 498) = 60.71
Model | 16.5822819 1 16.5822819 Prob > F = 0.0000
Residual | 136.016938 498 .273126381 R-squared = 0.1087
-----------+------------------------------ Adj R-squared = 0.1069
Total | 152.59922 499 .30581006 Root MSE = .52261
----------------------------------------------------------------------------
LGEARN | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-----------+----------------------------------------------------------------
S | .0664621 .0085297 7.79 0.000 .0497034 .0832207
_cons | 1.83624 .1289384 14.24 0.000 1.58291 2.089571
----------------------------------------------------------------------------
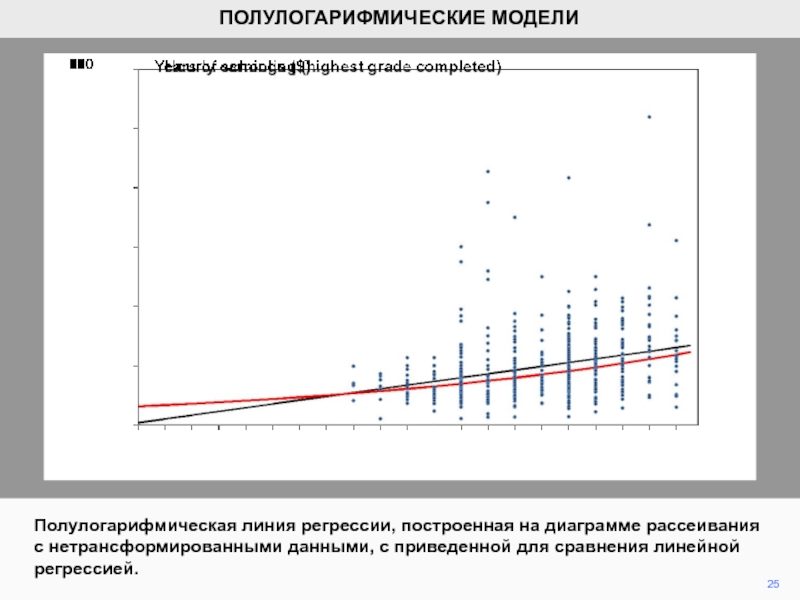
Слайд 25Полулогарифмическая линия регрессии, построенная на диаграмме рассеивания с нетрансформированными данными,
с приведенной для сравнения линейной регрессией.
25
ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
Слайд 2626
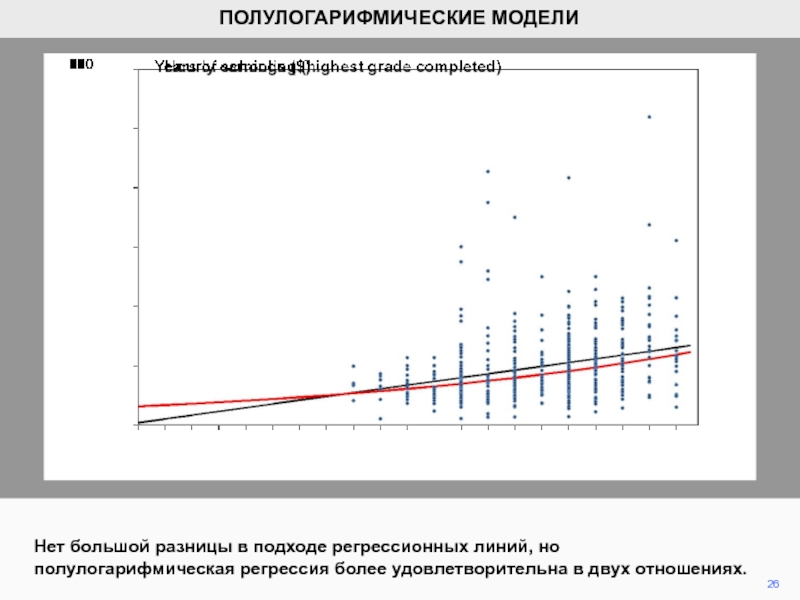
Нет большой разницы в подходе регрессионных линий, но полулогарифмическая регрессия
более удовлетворительна в двух отношениях.
ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ
Слайд 2727
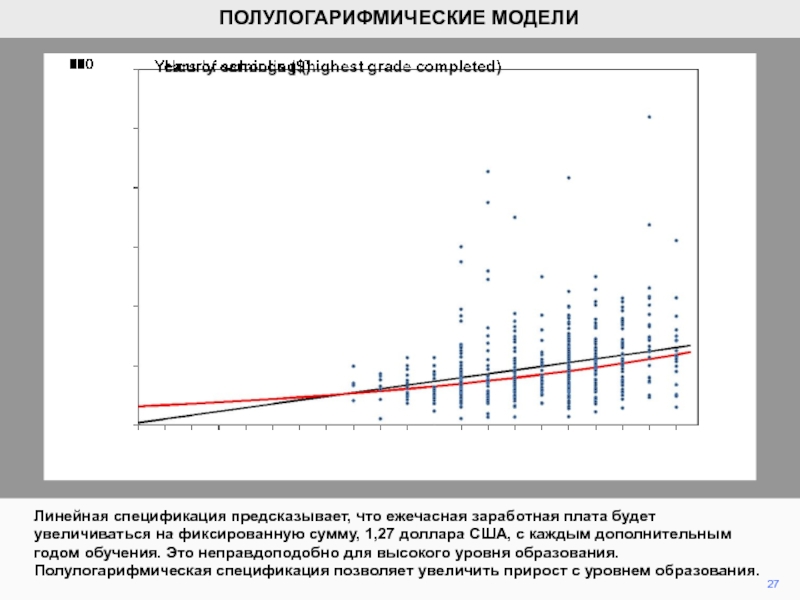
Линейная спецификация предсказывает, что ежечасная заработная плата будет увеличиваться на
фиксированную сумму, 1,27 доллара США, с каждым дополнительным годом обучения.
Это неправдоподобно для высокого уровня образования. Полулогарифмическая спецификация позволяет увеличить прирост с уровнем образования.ПОЛУЛОГАРИФМИЧЕСКИЕ МОДЕЛИ