нахождения первообразных
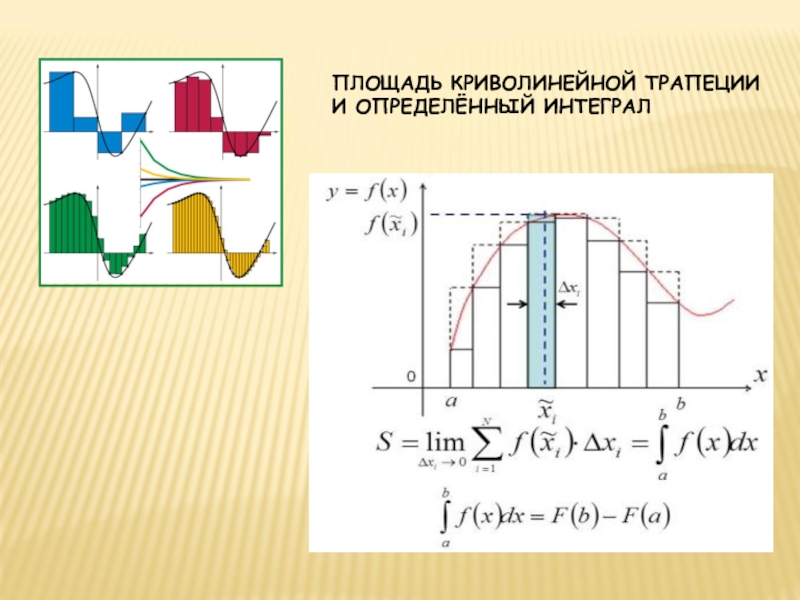
определенный интеграл
вычисление определенного интеграла
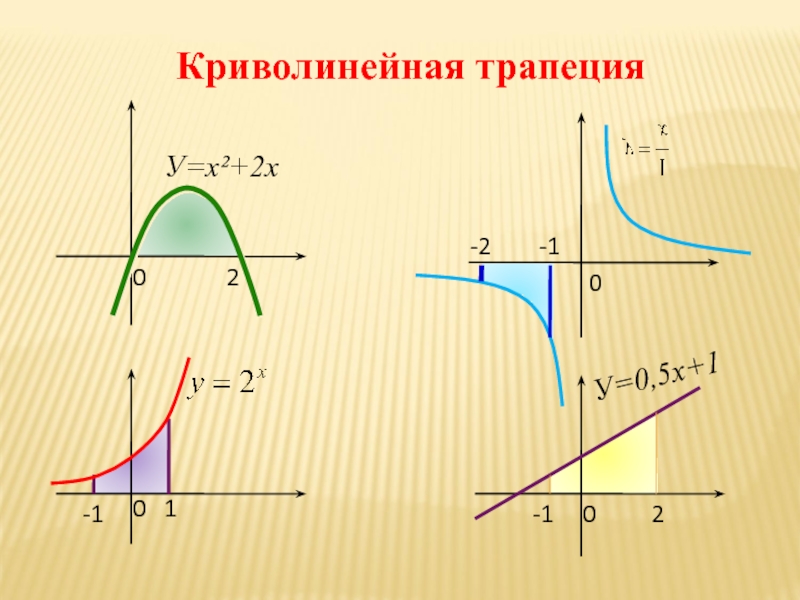
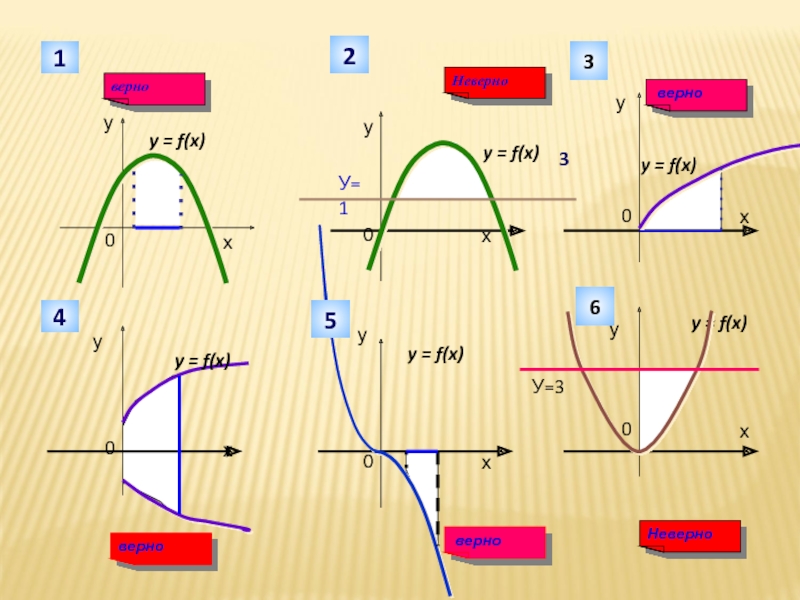
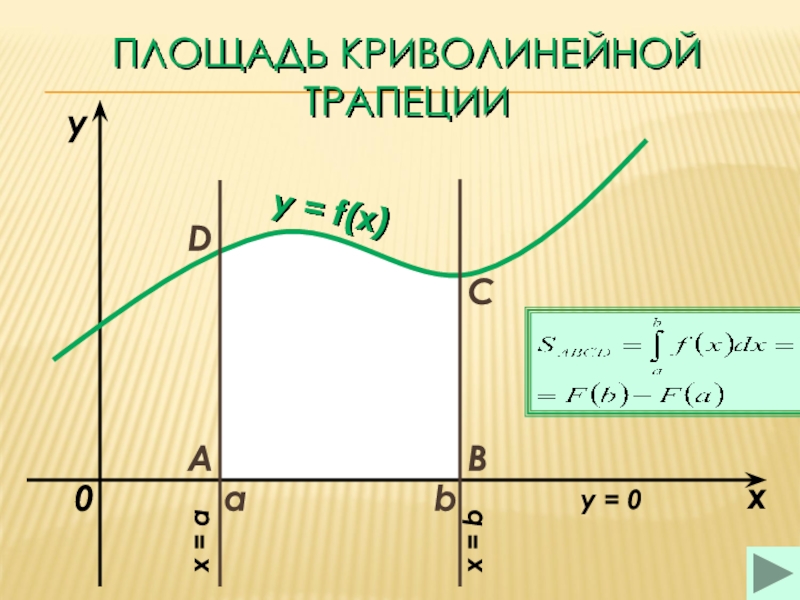
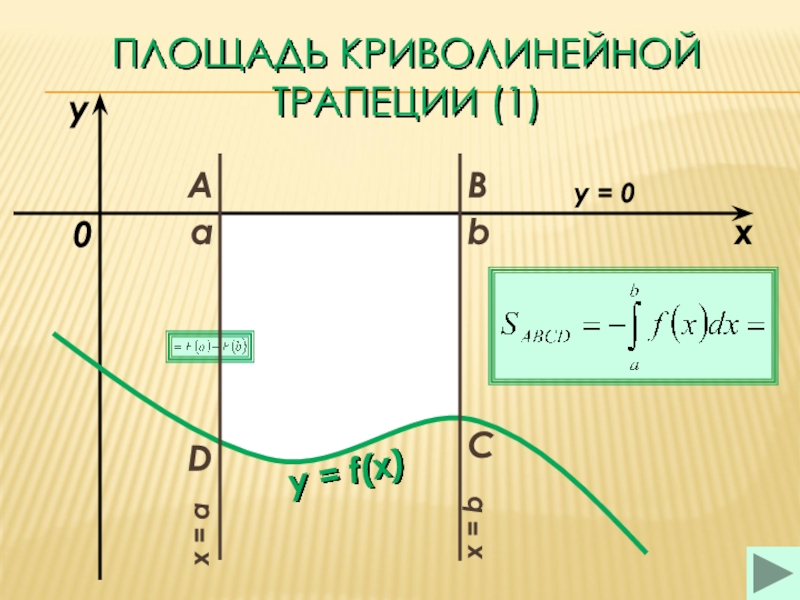
площадь криволинейной трапеции
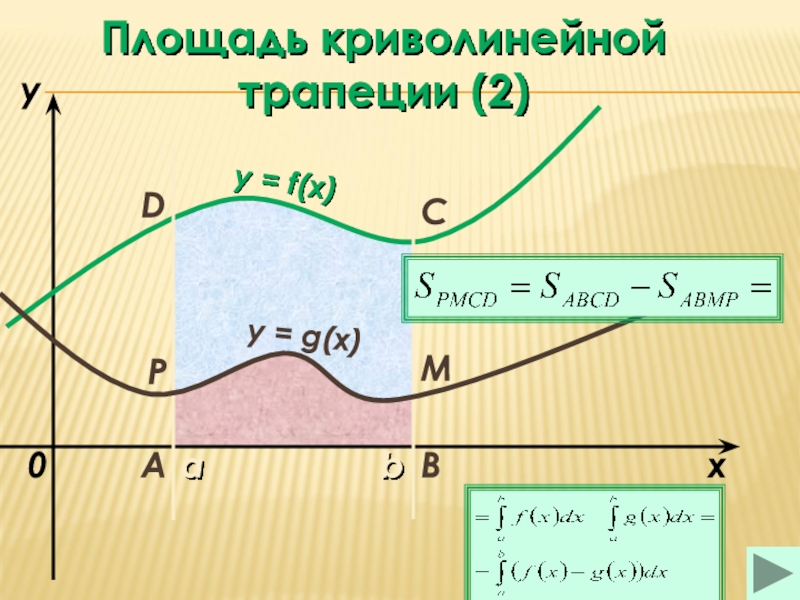
площадь криволинейной трапеции (1)площадь криволинейной трапеции (2)
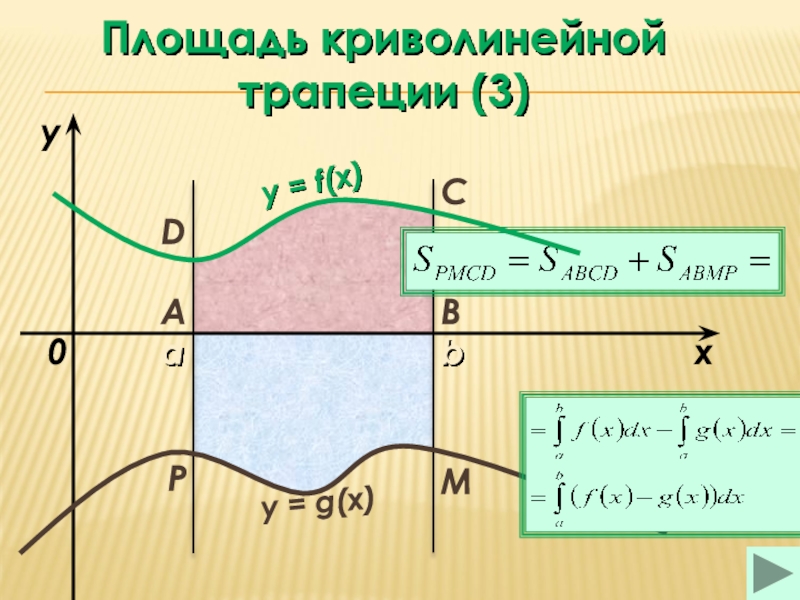
площадь криволинейной трапеции (3)
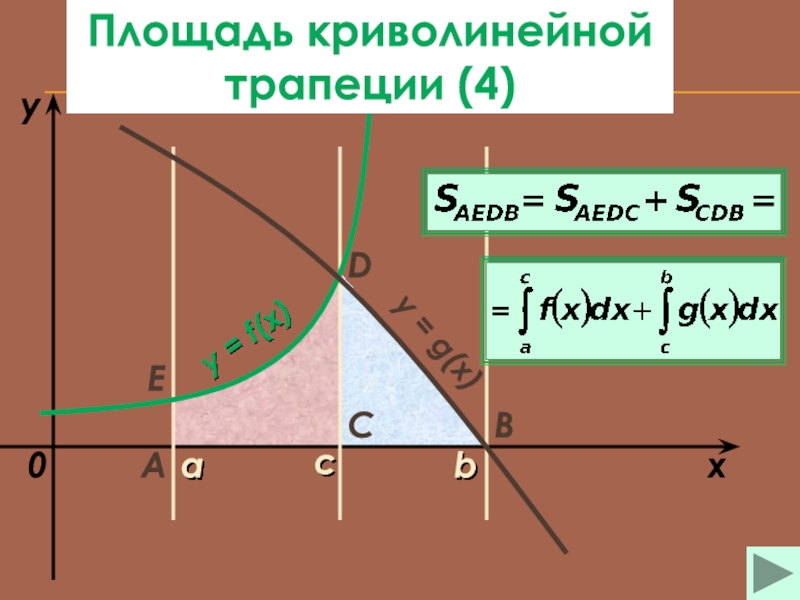
площадь криволинейной трапеции (4)
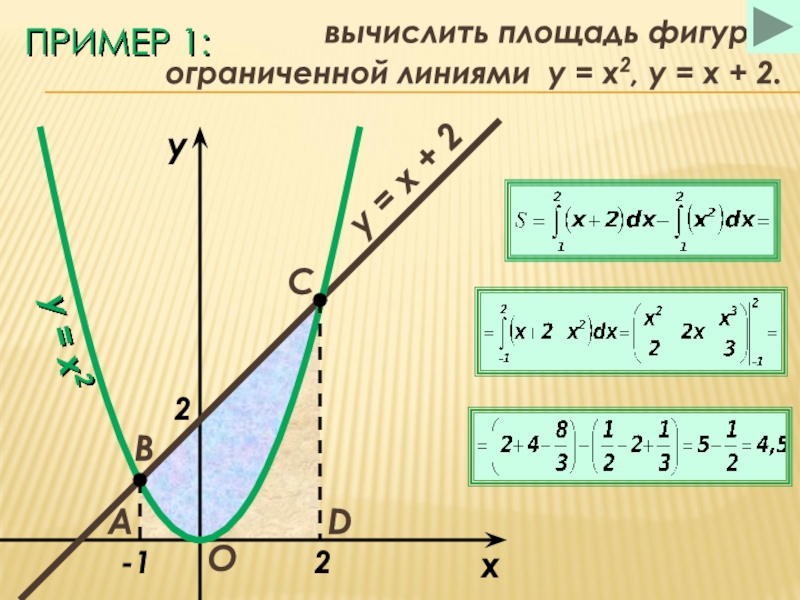
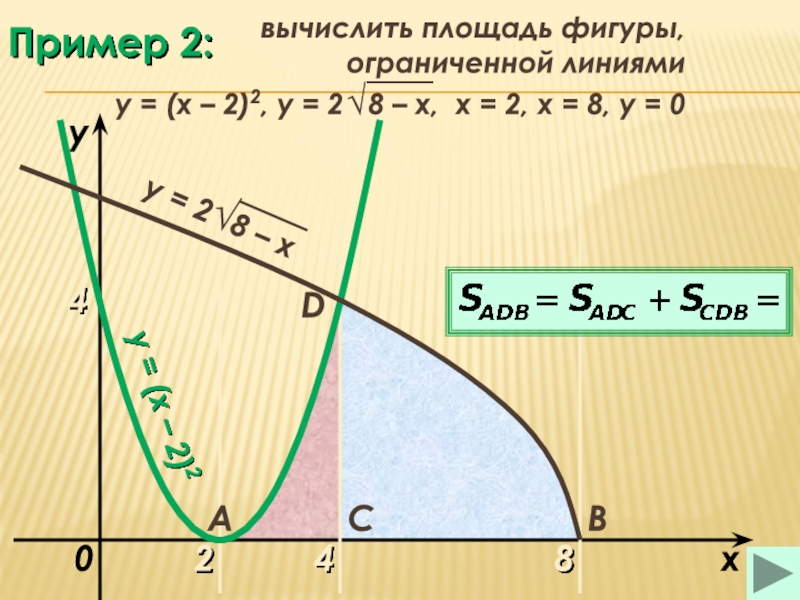
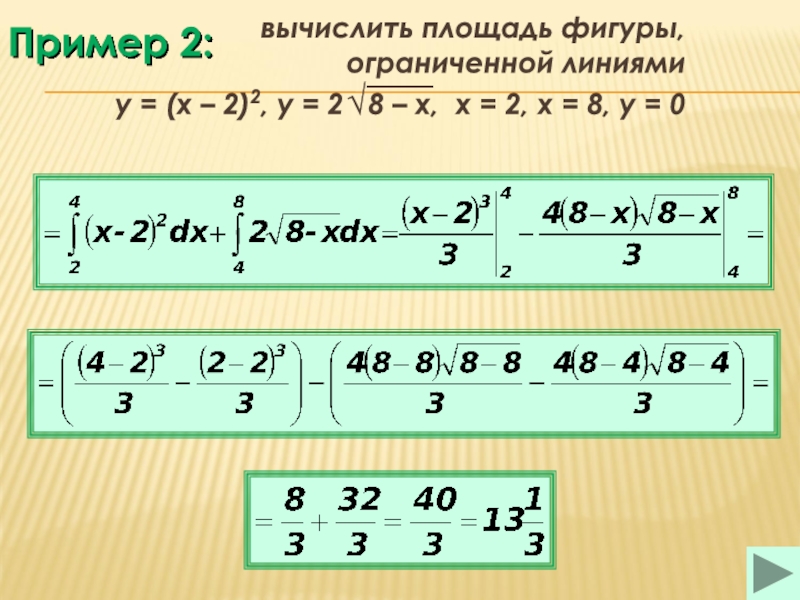
пример (1)
пример (2)













![Понятие первообразной Криволинейная трапецияОтрезок [a;b] называют основанием этой криволинейной трапецииКриволинейной трапецией называется фигура, Криволинейная трапецияОтрезок [a;b] называют основанием этой криволинейной трапецииКриволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющейна](/img/thumbs/96acf9599b81c7e4830917343d61c41c-800x.jpg)