Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Понятие вероятности обнаружения частицы Уравнение Шредингера для частиц,
Содержание
- 1. Понятие вероятности обнаружения частицы Уравнение Шредингера для частиц,
- 2. Корпускулярно-волновой дуализм Гипотеза Луи де Бройля о волновых свойствах микрочастицКорпускулярно-волновой дуализм электромагнитного излученияДифракция микрочастиц
- 3. Ф о
- 4. 7. В квантовой физике отсутствует наглядный образ фотона.
- 5. Корпускулярно – волновой дуализм электромагнитного излучения
- 6. Изображение поверхности золота в туннельном микроскопеВолны
- 7. Гипотеза де Бройля
- 8. Свободной частице с
- 9. Групповая скорость волны де Бройля
- 10. . Волна де Бройля не является
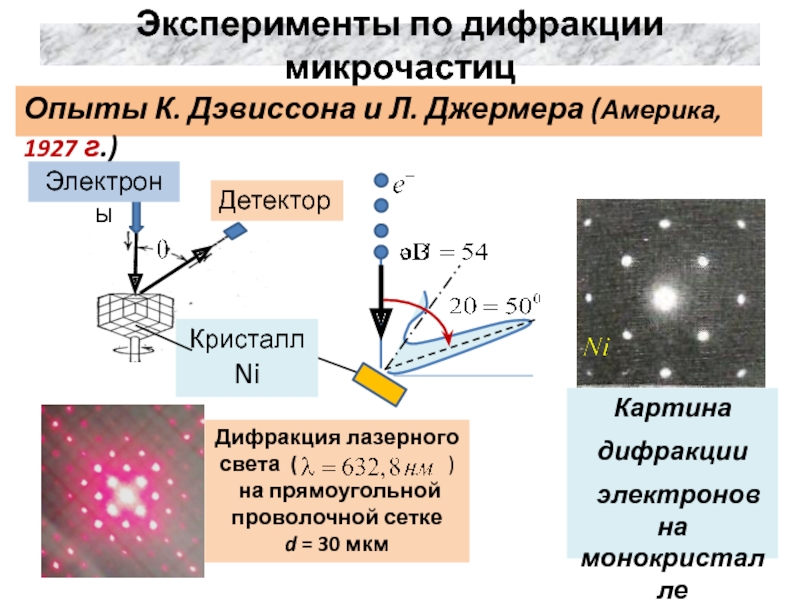
- 11. Эксперименты по дифракции микрочастицОпыты К. Дэвиссона и Л. Джермера (Америка, 1927 г.)
- 12. Отражение электронов от атомных плоскостей в кристалле.Атомная
- 13. Опыты Дж.П. Томсона (Англия, 1927 г.); П.С.
- 14. Дифракция электронов в поликристаллической фольгеВ опытах использовались
- 15. Дифракция одиночных электроновДифракция одиночных электронов
- 16. «Некоторые исследователи приступили к выполнению
- 17. Эксперименты, похожие на опыты
- 18. О новой механике движения микрочастиц – квантовой
- 19. Еще до начала экспериментов по
- 20. Принцип дополнительности Н. Бора.
- 21. Соотношения неопределенностей. Примеры мысленных экспериментов.
- 22. Слайд 22
- 23. Соотношения неопределенностей –
- 24. Следствия из соотношений неопределенностей
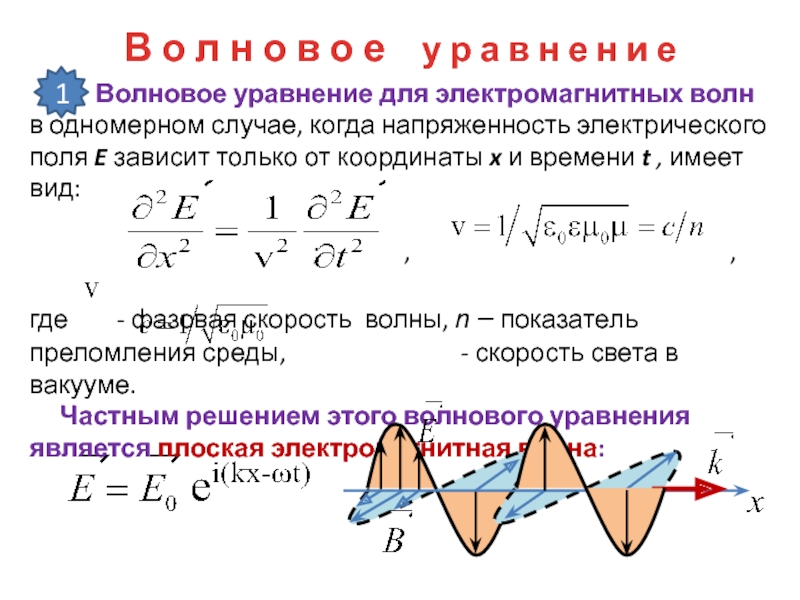
- 25. В о л н о в о
- 26. Волновое уравнение ШредингераВ 1926
- 27. Вероятностный смысл
- 28. В классической физике статистические
- 29. В квантовой физике, согласно
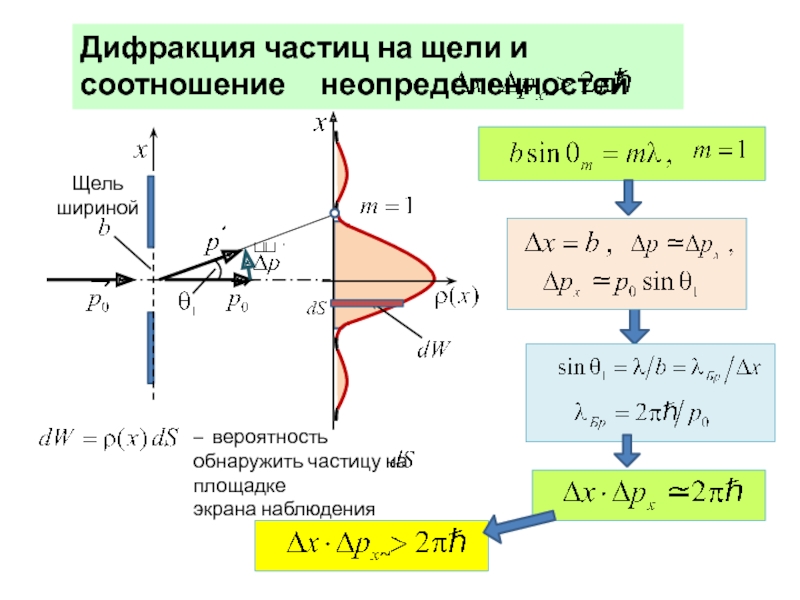
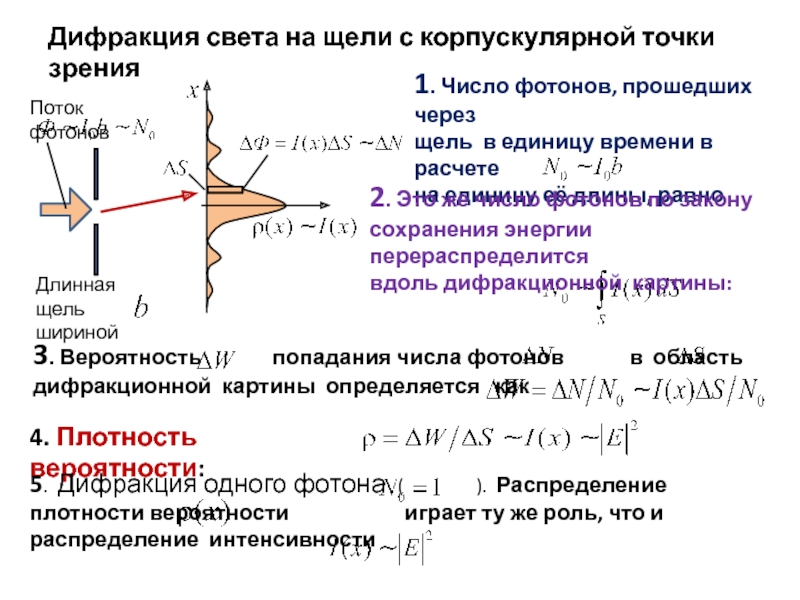
- 30. Дифракция света на щели с корпускулярной точки зрения
- 31. О вероятности обнаружения электрона, который свободно движется в направлении оси x
- 32. Уравнение Шредингера в символическом представлении
- 33. 2. Уравнение Шредингерагде потенциальная энергия – функция
- 34. Операторы импульса и энергии При таких
- 35. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Понятие вероятности
обнаружения частицы
Уравнение Шредингера
для частиц, скорость движения
которых мала по
сравнению
Слайд 2Корпускулярно-волновой дуализм
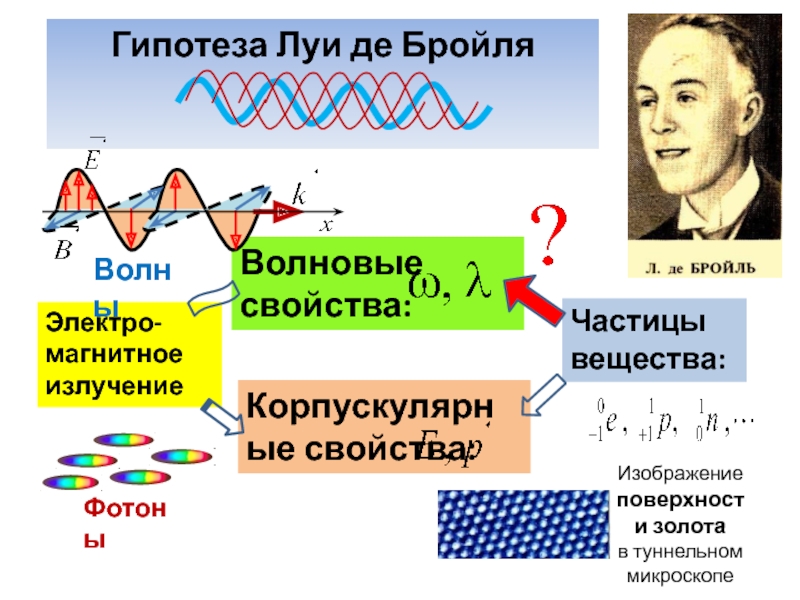
Гипотеза Луи де Бройля о волновых свойствах микрочастиц
Корпускулярно-волновой
дуализм
электромагнитного излучения
Дифракция микрочастиц
Слайд 3 Ф о т о н
Свет
и любое электромагнитное излучение – поток фотонов.
Корпускулярные свойства излучения.4. Фотон – стабильная элементарная частица, время жизни
которой определяется взаимодействием с веществом.
Слайд 7 Гипотеза де Бройля
В 1923 г. Французский физик Луи де Бройль выдвинул
чрезвычайно смелую гипотезу:Электромагнитное излучение и вещество, состоящее из микрочастиц, равноправны в отношении проявления корпускулярно-волновых свойств.
Микрочастицы должны проявлять волновые свойства.
Свет с длиной волны и частотой ведет себя как поток частиц (фотонов)
Частице с импульсом и энергией соответствует некий волновой процесс
Слайд 8 Свободной частице с энергией E и
импульсом p,
движущейся вдоль оси x, соответствует плоская волна де
Бройля:где - волновое число, - частота .
Волна распространяется в том же направлении, что и частица, и описывает её волновые свойства.
Плоская волна де Бройля
Слайд 9Групповая скорость волны де Бройля
Групповая
скорость световой волны:
Групповая скорость волны де Бройля:
Дифференцируя формулу связи между энергией E и импульсом p релятивистской частицы: , получим Учитывая, что
для групповой скорости находим
Групповая скорость волны де Бройля равна скорости движения частицы .
Слайд 10.
Волна де Бройля не является волной, движущейся вместе
с частицей.
Волна де Бройля и
частица – это один и тот же объект ! Понятие длины волны де Бройля характеризует этот объект с волновой точки зрения, а понятие импульса определяет свойства объекта как частицы, и эти два понятия связаны соотношением
, где или
Для частицы с кинетической энергией и
длина волны де Бройля равна
Для релятивистской частицы:
Слайд 12Отражение электронов от атомных плоскостей в кристалле.
Атомная структура кристаллов была
известна из опытов по дифракции рентгеновских волн. Еще в 1912
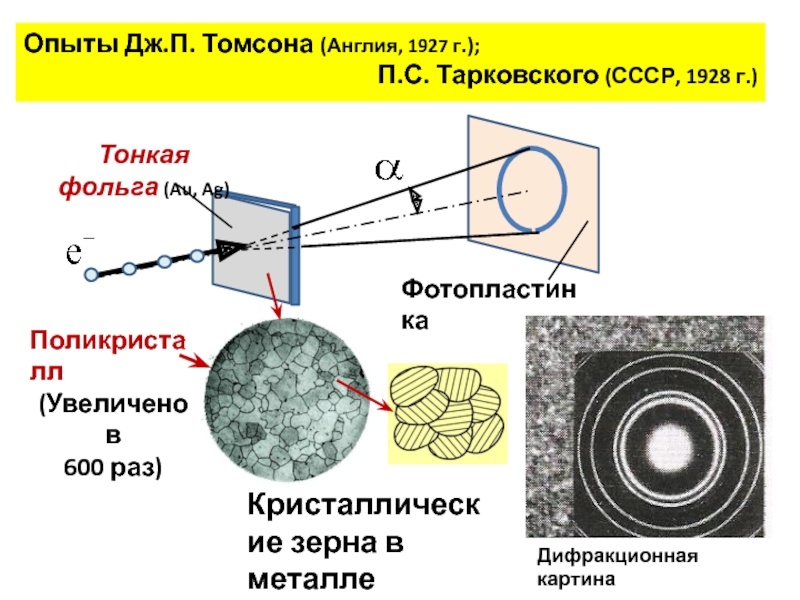
– 1913 гг. английские физики Г. Брэгг и Л. Брэгг (отец и сын) предложили вместо сложной дифракции от множества атомов рассматривать отражение волн от параллельных атомных плоскостей в кристалле и интерференцию отраженных волн.Слайд 13Опыты Дж.П. Томсона (Англия, 1927 г.);
П.С. Тарковского (СССР, 1928
г.)
Кристаллические зерна в металле
Поликристалл
(Увеличено в
600 раз)
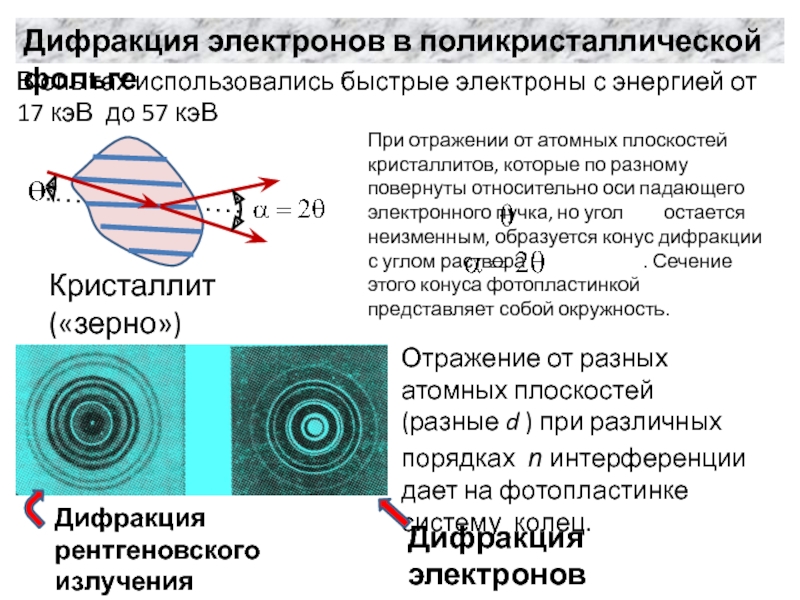
Слайд 14Дифракция электронов в поликристаллической фольге
В опытах использовались быстрые электроны с
энергией от 17 кэВ до 57 кэВ
Отражение от разных атомных
плоскостей (разные d ) при различных порядках n интерференции дает на фотопластинке систему колец.Слайд 15Дифракция одиночных электронов
Дифракция одиночных электронов
Группа
физиков во главе с В.А.Фабрикантом в СССР выполнила в 1949г
дифракционные исследования с очень слабым электронным пучком.В этих опытах интервал времени между двумя последовательными прохождениями электронов через поликристалл в 81 раз превышал время, затрачиваемое одним электроном на прохождение всего прибора. Таким образом, взаимодействие электронов друг с другом полностью исключалось, и электроны дифрагировали поодиночке.
Волновые свойства присущи отдельному электрону.
Слайд 16 «Некоторые исследователи приступили к выполнению опыта за который
ещё несколько лет назад их бы посадили в психиатрическую больницу
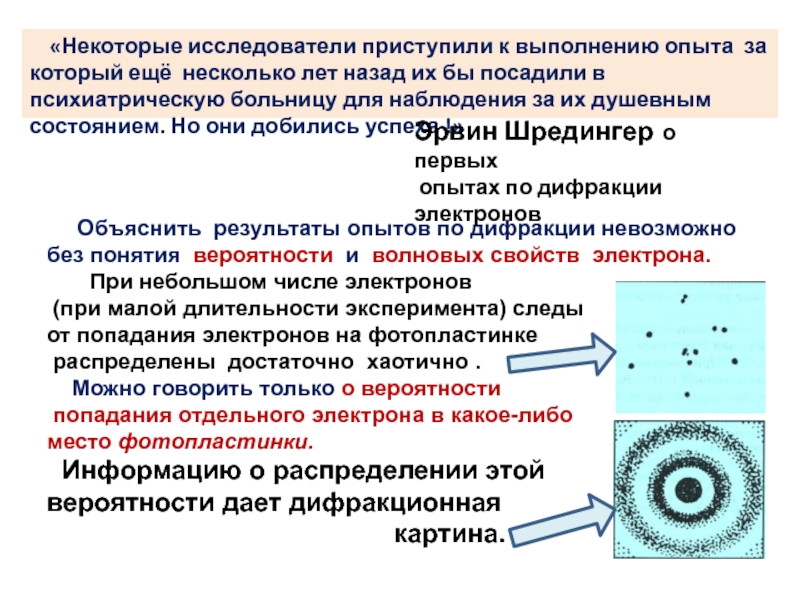
для наблюдения за их душевным состоянием. Но они добились успеха !» Объяснить результаты опытов по дифракции невозможно
без понятия вероятности и волновых свойств электрона.
При небольшом числе электронов
(при малой длительности эксперимента) следы
от попадания электронов на фотопластинке
распределены достаточно хаотично .
Можно говорить только о вероятности
попадания отдельного электрона в какое-либо
место фотопластинки.
Информацию о распределении этой
вероятности дает дифракционная
картина.
Эрвин Шредингер о первых
опытах по дифракции электронов
Слайд 17
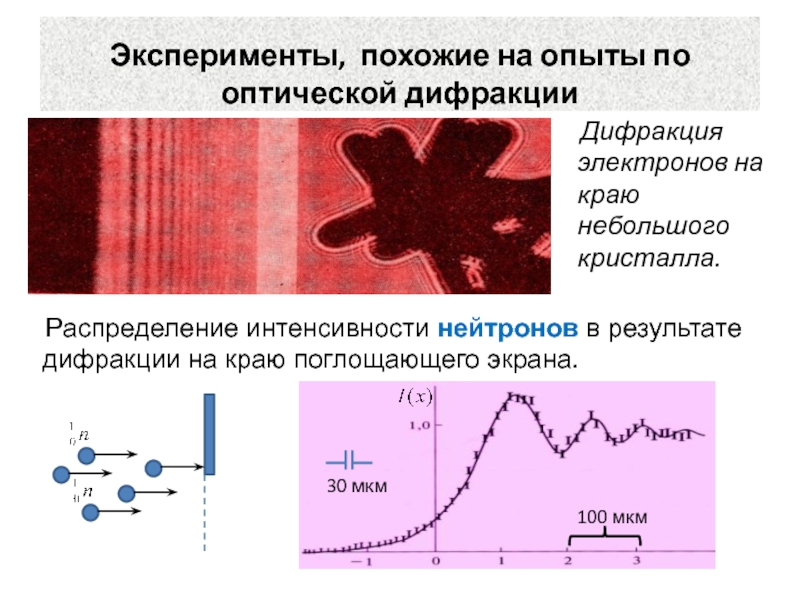
Эксперименты, похожие на опыты по оптической дифракции
Распределение интенсивности нейтронов
в результате дифракции на краю поглощающего экрана.
Слайд 18О новой механике движения микрочастиц – квантовой механике
На заре квантовой механики (1920-е годы) физики пытаются
найти законы, определяющие движение микрочастицы (электрона) в различных условиях, не прибегая к моделям внутренней структуры.Так например, электрон в дифракционных экспериментах с поликристаллической фольгой с некоторой вероятностью меняет свое направление движения после фольги, но фиксируется на фотопластинке как точечная частица.
Задача: Выяснить особенности физического и
математического описания движения микрообъекта,
совмещающего в себе каким-то образом
корпускулярные и волновые свойства.
Слайд 19 Еще до начала экспериментов по дифракции электронов
физики-теоретики
Вернер Гейзенберг в Германии
и Эрвин Шредингер в Австрии начали
разрабатывать новую механику, позволяющую рассчитывать волновое движение не только свободных микрочастиц, как это было у де Бройля, но и частиц , находящихся во внешнем потенциальном поле.В 1926 г. Шредингер получил свое знаменитое уравнение для волновой пси-функции и применил его к атому водорода, в котором единственный электрон находится в электрическом поле протона .
где ,
.
Уравнение Шредингера
Слайд 20Принцип дополнительности Н. Бора.
Соотношения неопределенностей
1927г. Нильс Бор в Дании сформулировал
принцип дополнительности в квантовых явлениях,
а мысленные эксперименты Вернера Гейзенберга в Германии привели к соотношениям неопределенностей, которые являются математическим воплощением общей идеи дополнительности в квантовых явлениях.
Принцип дополнительности Бора: В области квантовых явлений
наиболее общие физические свойства какой-либо системы описываются
с помощью дополняющих друг друга пар независимых переменных ,
каждая из которых может быть лучше определена только за счет
уменьшения степени определенности другой.
Такими переменными являются: импульс – координата ; энергия – время; частица – волна; непрерывность – дискретность; … .
«Физическая картина явления и его математическое описание дополнительны.
Создание физической картины требует пренебрежения деталями и уводит от математической точности. И наоборот, попытка точного математического описания
явления затрудняет ясное понимание» (А. Б. Мигдал)
Слайд 23 Соотношения неопределенностей – частный случай и
конкретное выражение принципа дополнительности Н. Бора.
Соотношения неопределенностей В. Гейзенберга
Слайд 24Следствия из соотношений неопределенностей
Н.Бор часто вспоминал,
как в 50-х годах к нему после лекции подошел студент
и спросил: « Неужели действительно были такие идиоты, которые думали, что электрон в атоме вращается по орбите»Слайд 26 Волновое уравнение Шредингера
В 1926 г. австрийский физик-теоретик
Эрвин Шредингер разработал теорию движения микрочастиц, в основу которой положил
уравнение2
Движение в трехмерном пространстве;
Слайд 28 В классической физике статистические методы, использующие
понятие
вероятности, рассматриваются как вспомогательные,
и применяются в тех случаях, когда
недостаточно знаний о подробностях того или иного события.
Так обстоит дело, например, в кинетической теории газов, где
предполагается, что каждая частица во всякий данный момент
времени имеет определенное значение скорости.
Но частиц много, уследить за всеми невозможно,
и единственный реальный путь заключается в том,
чтобы найти закономерности в этом хаотичном
движении многих частиц – вычислить вероятность
распределения частиц по скоростям.
Вероятность в классической физике
Слайд 29 В квантовой физике, согласно М.Борну, ситуация совсем
иная.
Электронам, протонам, фотонам и другим частицам присущи
волновые свойства.
Нет смысла, например, говорить о локализации световой волны после дифракции на щели или траектории фотонов.
Фотон может попасть в любое место экрана наблюдения
с той или иной вероятностью. Это касается и микрочастиц, для
описания движения которой понятие определенной и
непрерывной траектории оказывается неприменимым.
При рассмотрении процессов , происходящих в микромире,
неизбежно приходится использовать понятие
волны вероятности
Вероятность в квантовой физике
Слайд 32Уравнение Шредингера в символическом представлении
Макс Борн
в том же 1926 году высказал идею , суть
которой
состояла в сопоставлении классической физической величине некоторого линейного оператора, обладающего
определенными свойствами.
1. Об идее М. Борна и операторах в математике.
Слайд 332. Уравнение Шредингера
где потенциальная энергия – функция координат,
ей соответствует
оператор умножения:
.Слайд 34Операторы импульса и энергии
При таких операторах квантовое уравнение
в символической
форме является уравнением Шредингера
где оператор Гамильтона
(оператор полной энергии).