Поток и стенки

на стенки канала
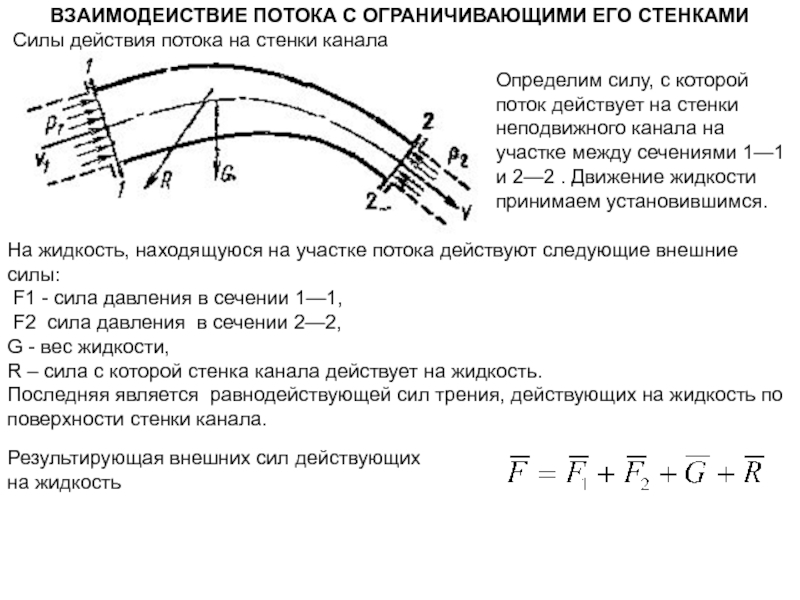
На жидкость, находящуюся на участке потока действуют следующие

Определим силу, с которой поток действует на стенки неподвижного канала на участке между сечениями 1—1 и 2—2 . Движение жидкости принимаем установившимся.

Результирующая внешних сил действующих на жидкость

потока;
вектор —

динамическая составляющая реакции потока.
Силы давления

определяется разностью давлений жидкости на внутреннюю поверхность стенки и атмосферного

р1 и р2 — давление в центрах тяжести входного и выходного сечений

S1 и S2 — площади входа и выхода сечений потока

Жидкость вытекает из резервуара через колено и присоединенный к нему насадок.

Определим силы, нагружающие болтовые группы фланцевого соединения А. Вес колена и насадка учитывать не будем

отрежем колено и насадок. Рассмотрим их равновесие. На отрезанные колено

Спроектировав все силы па горизонтальное и вертикальные направления получим

В атом случае движение жидкости является сложным, ее частицы
движутся, во- первых относительно канала, во- вторых они вместе
с каналом совершают переносное движение. Относительное движение жидкости принимаем установившимся.
Кроме рассмотренных выше сил действуют переносная сила инерции и кориолисова сила инерции

Сила действия потока на стенки движущегося канала

из отверстия или насадка, на неподвижную стенку. Рассмотри сначала стенку

Сечениями 1—1 и 2—2 выделим участок потока. Сечение 2—2 представляет собой поверхность вращения. Так как давления во входном 1—1 и выходном 2—2 сеч. равны атмосферному, то силы и давления равны нулю. Весом выделенного участка потока пренебрегаем. При этом реакция потока

Если пренебречь весом жидкости и, следовательно, разностью высот различных точек сечения 2—2. а также гидравлическим сопротивлением, то из уравнения Бернулли, написанного для сечений 1-1 и 2—2 получим, что скорости в этих сечениях одинаковы. Ввиду осевой симметрии потока сила его действия на стенку направлена вдоль оси. Спроектировав на это направление векторы сил, входящих в уравнение, получим

потоку

2. Стенка имеет чашеобразную форму. Струя поворачивает на угол =

углом а к оси струи
Принимаем, что жидкость растекается по

Предположим, что силы трения по поверхности стенки пренебрежимо малы. При этом сила N действия струи на стенку направлена перпендикулярно к стенке. Выделим сечениями 1—1 2—2 и З—З уча сток потока. Так как силы, давления, действующие в сечениях равны нулю, а вес жидкости пренебрежимо мал статическая реакция потока равна нулю и сила действия потока на стенку

к стенке, и направление х, параллельное ей, получим
Если пренебречь гидравлическими

Согласно уравнению расходов

Определив расходы, можно найти действующие силы.