Практическое занятие 4 Механические свойства твердых тел (ТТ). Деформации 1

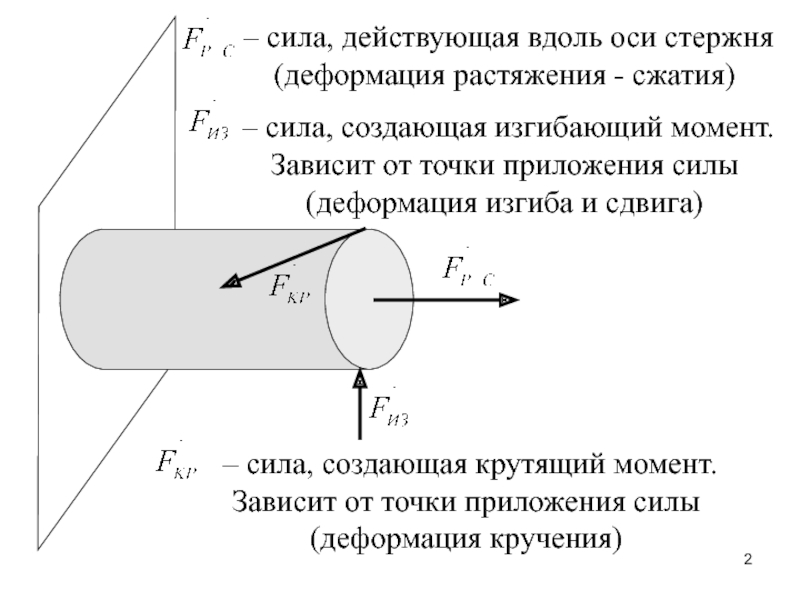
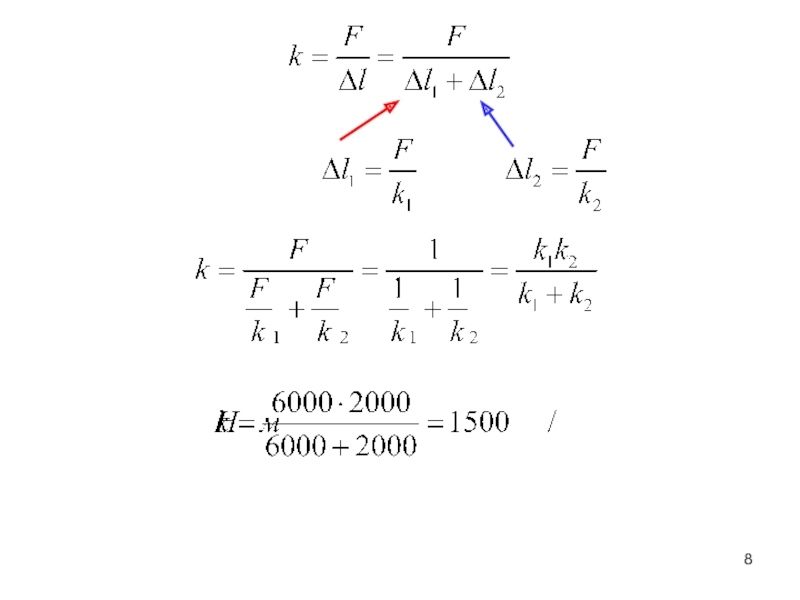
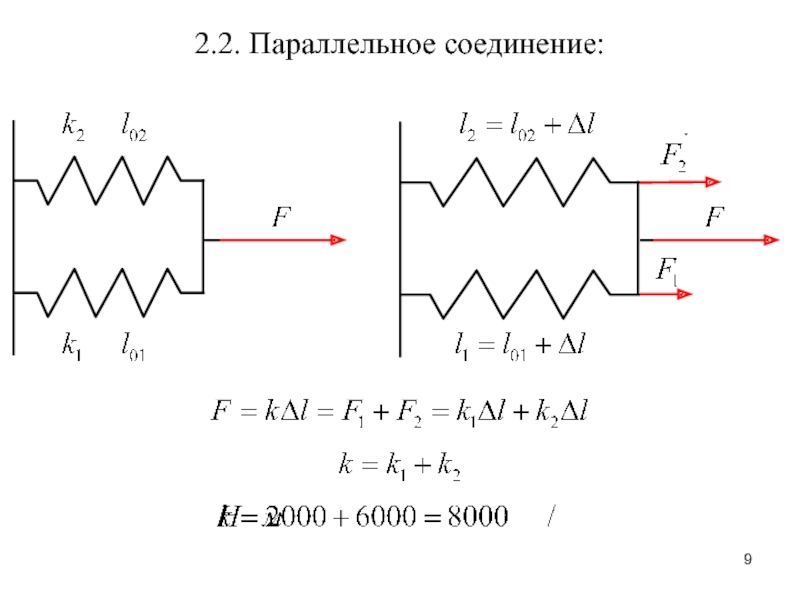
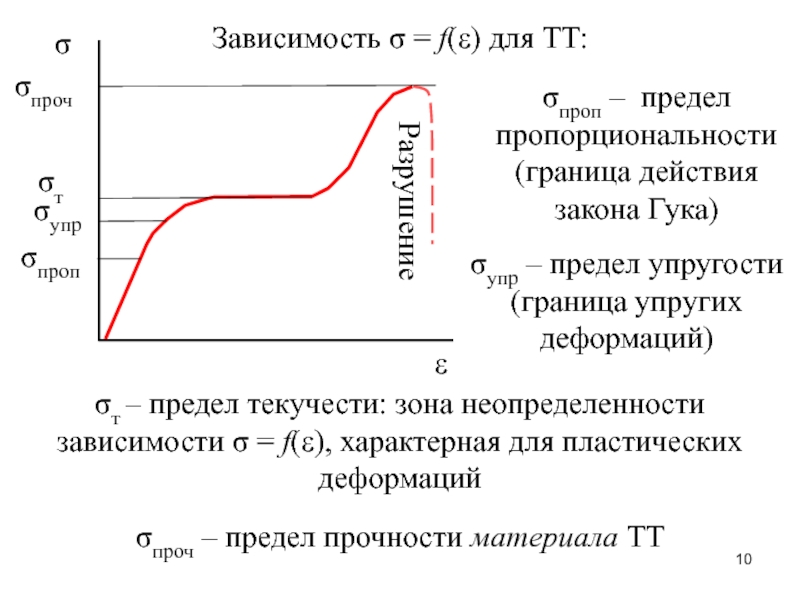
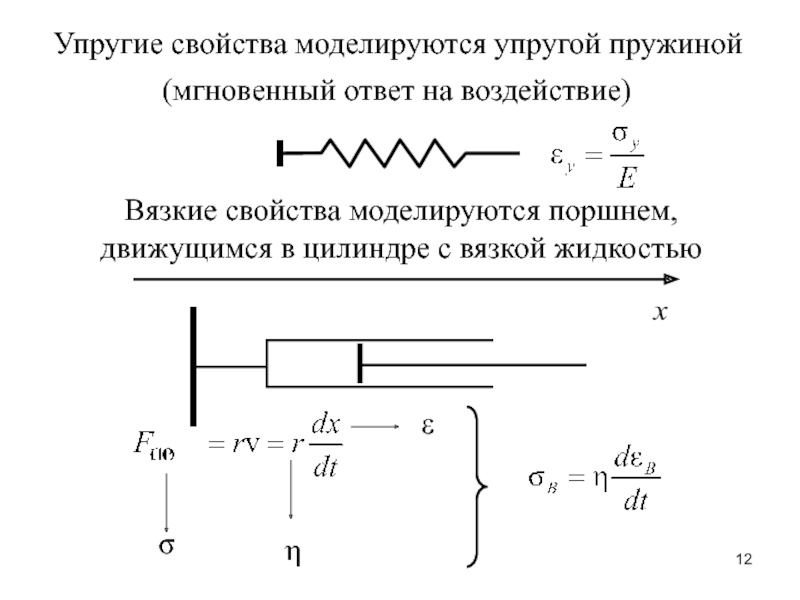
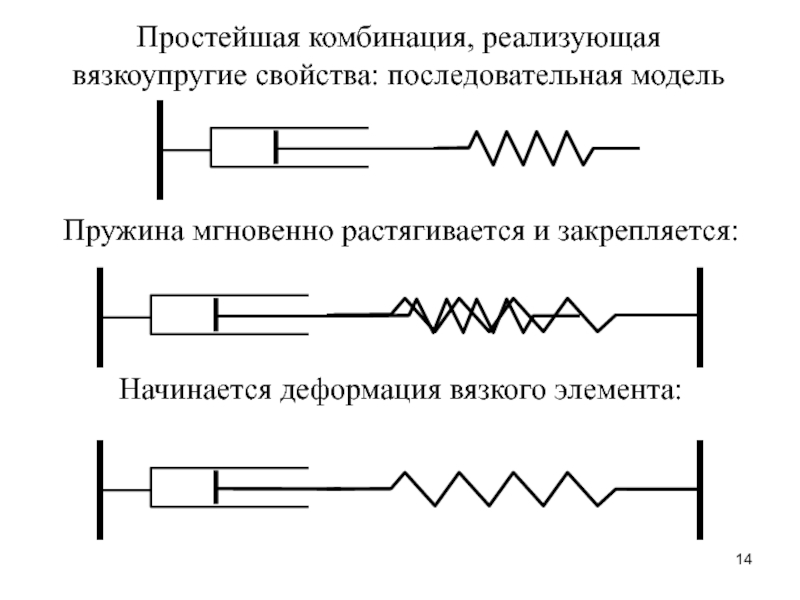
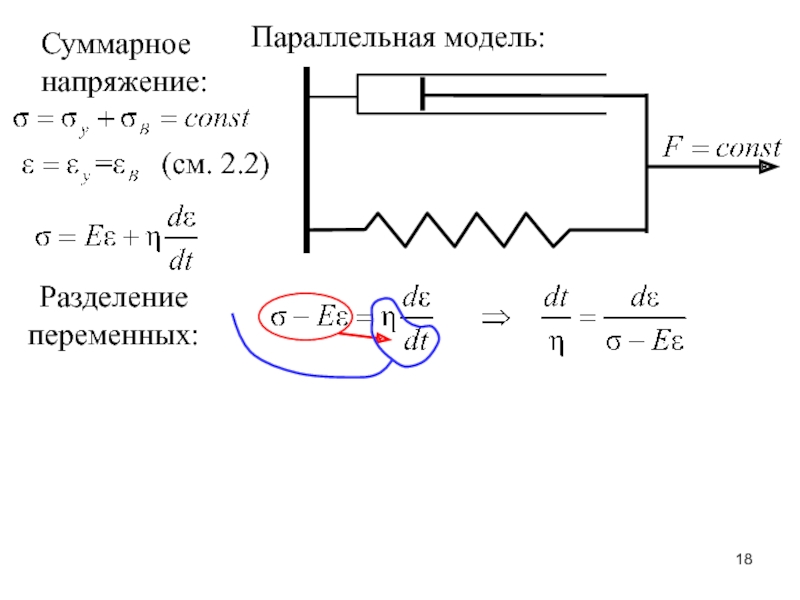
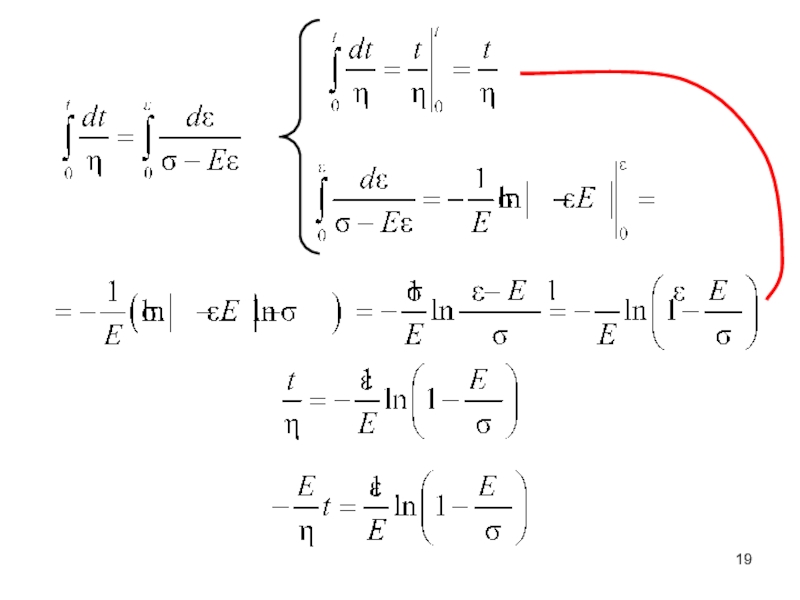
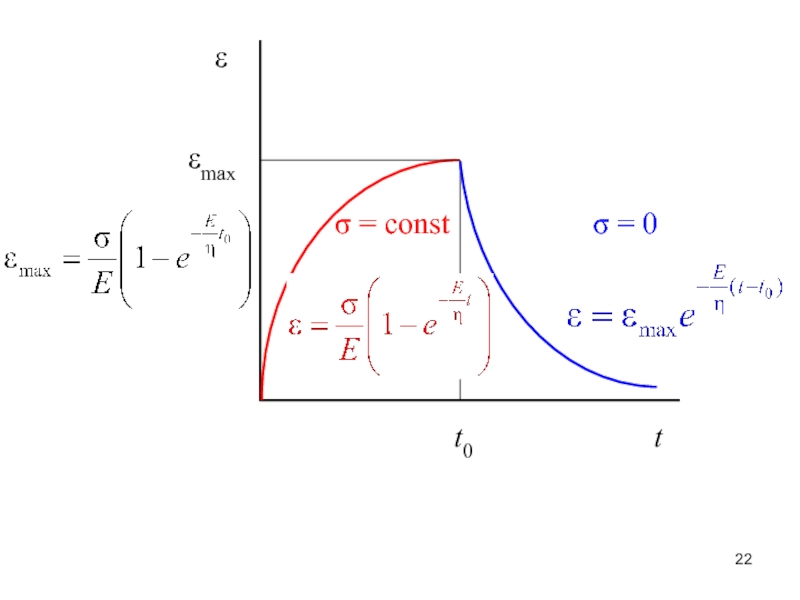
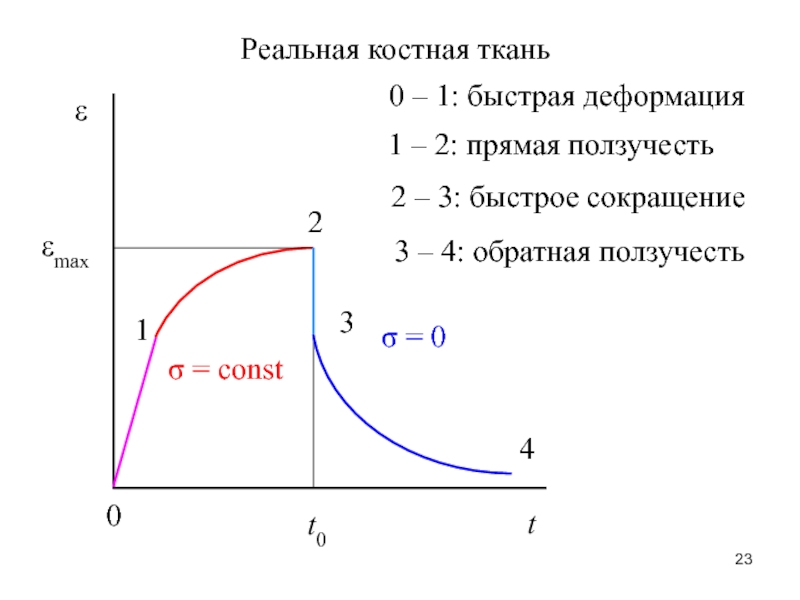
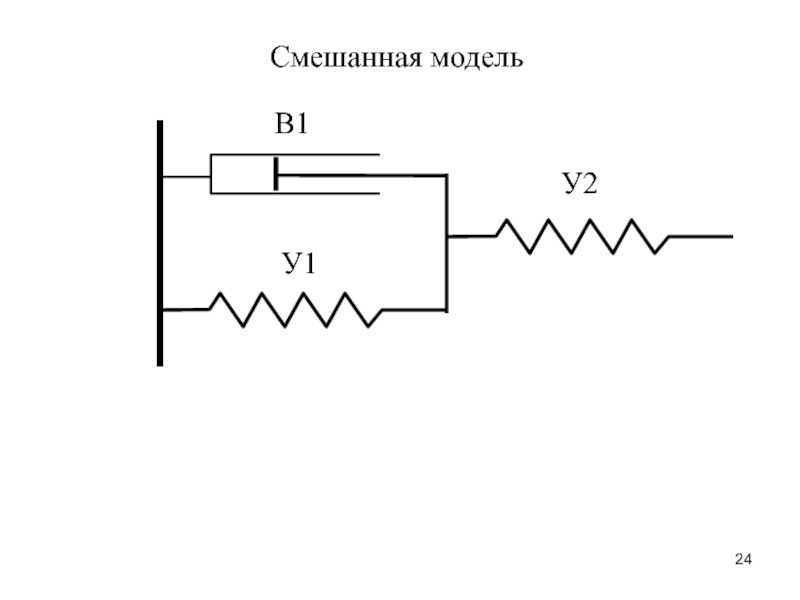
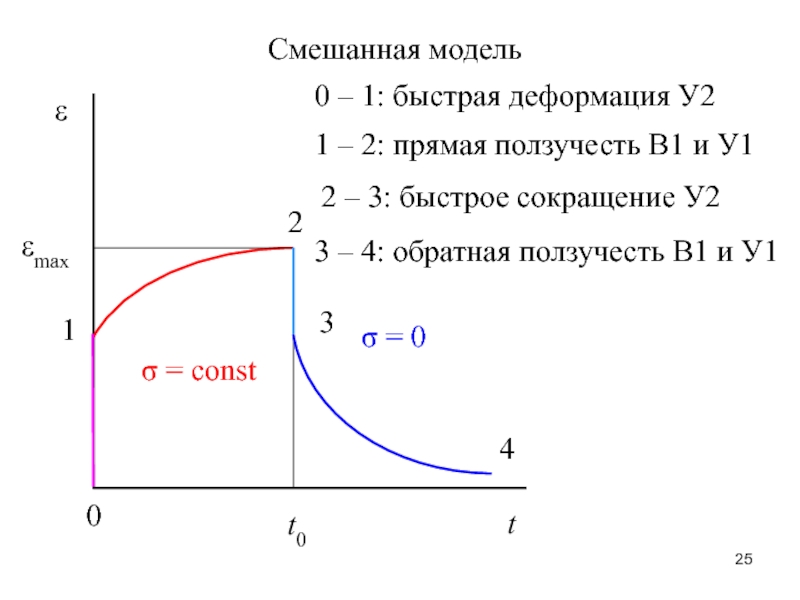
– сила, создающая изгибающий момент.
Зависит от точки приложения силы
(деформация изгиба

– сила, создающая крутящий момент.
Зависит от точки приложения силы
(деформация кручения)

свои форму
и размеры
Кристаллические и
поликристаллические тела
при малых деформациях
Пластические

после снятия нагрузки ТТ
частично
восстанавливает свои форму
и размеры

Кристаллические ТТ при
больших деформациях
аморфные тела,
полимеры

+
||

сечении цилиндра
Закон Гука для малых
упругих деформаций:
– относительная
деформация
причина
свойство
следствие
k

Упругие деформации:

Для ТТ в целом:

Δl – абсолютная
деформация цилиндра

Для вещества ТТ:

Аналогия:

удлиняется на 3,3 мм. Сухожилие можно считать
круглым в сечении

СИ:

Закон Гука:

параллельном их соединении.
Жесткости пружин k1=2000 Н/м и k2=6000 Н/м.
2.1.

Гука)
σупр – предел упругости
(граница упругих
деформаций)
σт – предел текучести: зона неопределенности

σпроч – предел прочности материала ТТ

может выдержать кость,
не разрушаясь? Предел прочности бедренной кости
при

СИ:

S = 3,0 см2 = 3,0·10-4 м2
σпроч. = 124 МПа = 124·106 Па

Fmax = ?

Закон Гука:

моделируются поршнем,
движущимся в цилиндре с вязкой жидкостью
х
σ
η
ε

дальнейшем – просто деформации)
σу и σВ – напряжения упругой и

r – коэффициент сопротивления вязкой среды

η – коэффициент динамической вязкости среды
(см. Лекция 3)

закрепляется:
Начинается деформация вязкого элемента:

и вязкой деформаций при
последовательном соединении равны (задача 2.1):

– напряжение в элементах в начальный момент времени
(мгновенная деформация и

σ

t

σ0

εmax:
Пружина начинает сжиматься, перемещая поршень:

деформация
2
1 – 2: прямая ползучесть
3
2 – 3: быстрое сокращение
4
3

У2
2
1 – 2: прямая ползучесть В1 и У1
3
2 –

4

3 – 4: обратная ползучесть В1 и У1

Иметь при себе распечатанные выдачи лекции №3