Слайд 3Энтропийное кодирование
Алгоритм сжатия Хаффмана
320×240×2 =150 Кбайт
150×30=4.5 Мбайт
Таблица частот
(исходная таблица) метода Хаффмана
Полная частотная таблица
Число 0
1 2 3 4 5 6 7 254 255
Частота | 0 | 10 l 20 | 30 l 5 | 25 l 0 | 10 | 0 | 0 |
Ненулевая часть частотной таблицы
Число 1 2 3 4 5 7
Частота | 10 | 20 | 30 | 5 | 25 | 10
1, 2, 3, 4, 5, 7.
100 байт
сжатие без потерь (или полностью обратимое);
сжатие с потерями (когда несущественая часть данных утрачивается и полное восстановление невозможно).
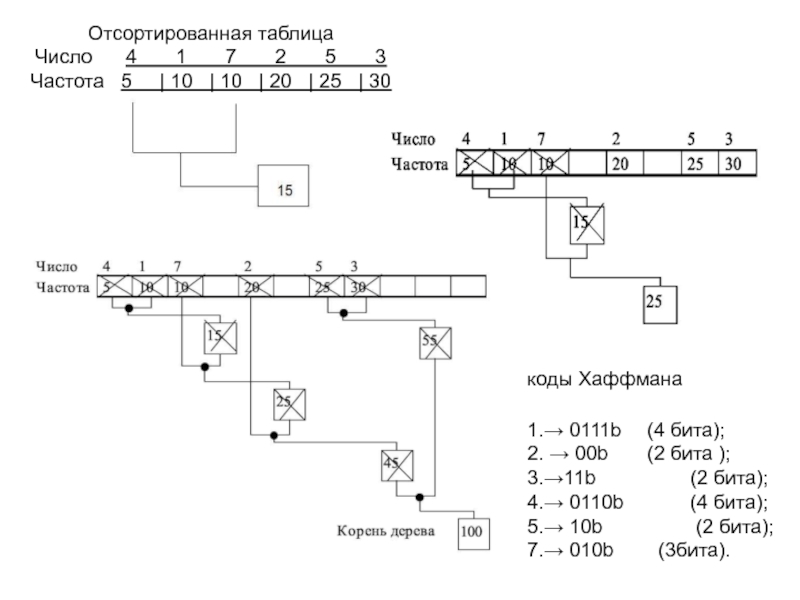
Слайд 41.→ 0111b (4 бита);
2. → 00b (2 бита );
3.→11b
(2 бита);
4.→ 0110b
(4 бита);
5.→ 10b (2 бита);
7.→ 010b (3бита).
Отсортированная таблица
Число 4 1 7 2 5 3
Частота 5 | 10 | 10 | 20 | 25 | 30
коды Хаффмана
Слайд 5Ссылка на узел ---0 до 511 (для байта), --- номер
узла в массиве узлов
Информация по дереву 2х 9(бит) х
5 (узлов) -------90 бит
Первоначально --------800 бит
После сжатия размер сжатых данных: 240 бит и 90 бит данных о дереве
Размер степени сжатия данных --- 0,41 от исходного.
Слайд 6Преобразование Фурье функции f является интегральным представлением этой функции задается
следующей формулой
Слайд 7Дискретное преобразование Фурье , ДПФ
Т
.
Периодический аналоговый сигнал .
имеющий период Т. может быть представлен в виде суммы косинусоидальных
и синусоидальных (гармонических) колебаний с частотами, кратными частоте
повторения этого сигнала
Гармоники , ПФ
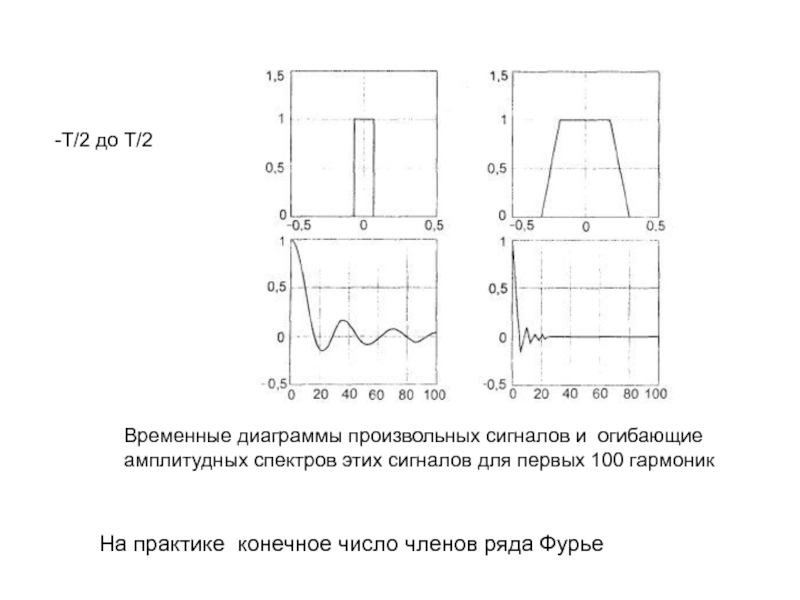
Слайд 9Временные диаграммы произвольных сигналов и огибающие амплитудных спектров этих сигналов
для первых 100 гармоник
-Т/2 до Т/2
На практике конечное число
членов ряда Фурье
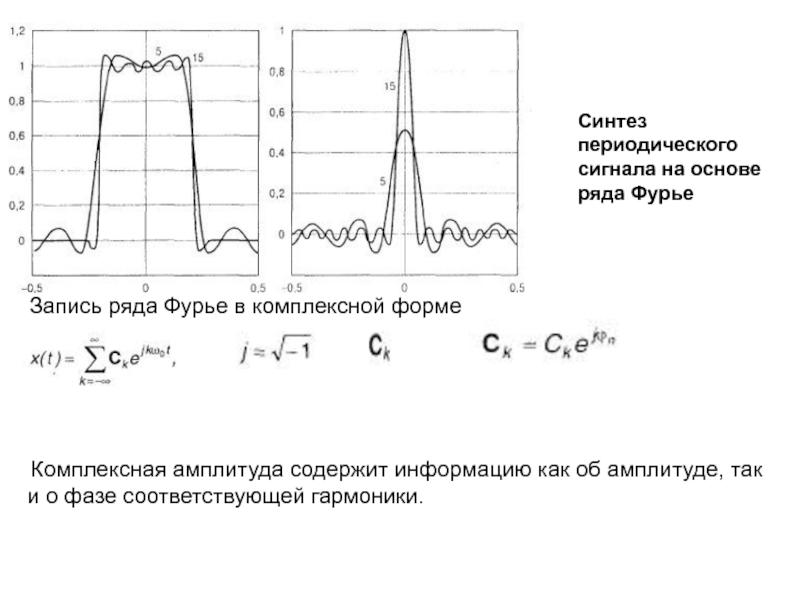
Слайд 10Синтез периодического сигнала на основе ряда Фурье
Запись ряда Фурье в
комплексной форме
Комплексная амплитуда содержит информацию как об амплитуде, так
и о фазе соответствующей гармоники.
Слайд 11Дискретный сигнал х(п), отличный от 0 при n = 0,1..,
n-1. Такой сигнал также можно представить в виде суммы гармонических
функций.
Сумма будет содержать конечное число n слагаемых, каждое из которых представляет собой дискретную комплексную гармоническую функцию.
где
Нахождение коэффициентов
прямое дискретное преобразование Фурье
→
[ рад/с ]
в ДПФ соответствует безразмерная величина ..
Отношение А/π показывает, какую часть частоты дискретизации составляет частота данной дискретной гармоники.
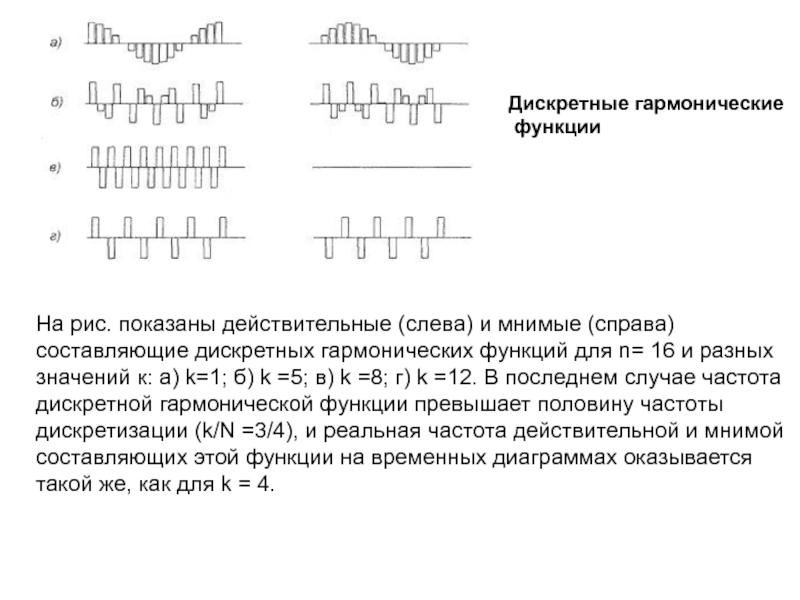
Слайд 12Дискретные гармонические
функции
На рис. показаны действительные (слева) и мнимые
(справа) составляющие дискретных гармонических функций для n= 16 и разных
значений к: а) k=1; б) k =5; в) k =8; г) k =12. В последнем случае частота дискретной гармонической функции превышает половину частоты дискретизации (k/N =3/4), и реальная частота действительной и мнимой составляющих этой функции на временных диаграммах оказывается такой же, как для k = 4.
Слайд 13Одномерный сигнал (а) и
модуль его ДПФ (б)
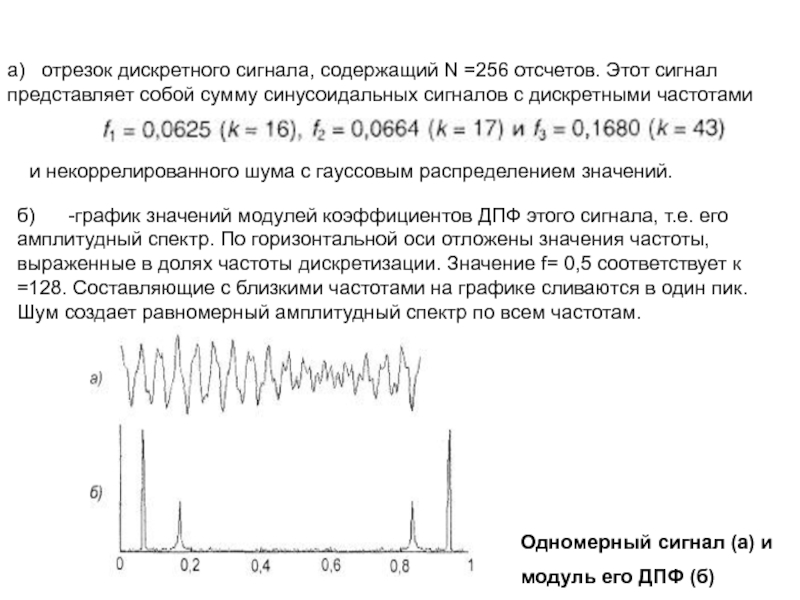
а) отрезок
дискретного сигнала, содержащий N =256 отсчетов. Этот сигнал представляет собой
сумму синусоидальных сигналов с дискретными частотами
и некоррелированного шума с гауссовым распределением значений.
б) -график значений модулей коэффициентов ДПФ этого сигнала, т.е. его амплитудный спектр. По горизонтальной оси отложены значения частоты, выраженные в долях частоты дискретизации. Значение f= 0,5 соответствует к =128. Составляющие с близкими частотами на графике сливаются в один пик. Шум создает равномерный амплитудный спектр по всем частотам.
Слайд 1414 -7
Дискретное косинусное преобразование (англ. Discrete Cosine Transform — сокр.
DCT) ДКП— одно из ортогональных преобразований. Вариант для вектора действительных
чисел
Математически преобразование можно осуществить умножением вектора на матрицу преобразования
Существуют аналоги DCT, приближающие косинус числами, легко получающимися путём небольшого количества операций сдвига и сложения, что позволяет избежать операций умножения и тем самым повысить эффективность вычислений
Дискретное косинусное преобразование представляет собой разновидность преобразования Фурье и имеет обратное преобразование.
В DCT картинка рассматривается как совокупность пространственных волн, для которых оси X и Y проводятся параллельно продольной и поперечной осям картинки, а по оси Z откладывается значение цвета соответствующего пикселя изображения.
Чтобы иметь дело только с действительными числами, обычно используют разложение с помощью ДПК
Слайд 1514 -8
Дискретное косинусное преобразование (ДКП).
Слайд 1614 -9
Коэффициенты двумерного прямого ДКП определяются по формулам
Обратное двумерное
ДКП имеет вид
Слайд 17Дискретное косинусное преобразование (. Discrete Cosine Transform, DCT) — одно из ортогональных
преобразований .
Вариант косинусного преобразования для вектора действительных чисел. Применяется
в алгоритмах сжатия информации с потерями, например, MPEG и JPEG. Это преобразование тесно связано с дискретным преобразованием Фурье.
Математически преобразование можно осуществить умножением вектора на МАТРИЦУ преобразования. При этом матрица обратного преобразования с точностью до множителя равна траспонированной МАТРИЦЕ .
В математике матрицы выбирают так, чтобы преобразование было ортонормированным, а постоянный множитель равен единице.
Слайд 1814 -10
Некоторые из базисных функций двумерного ДКП 8x8 элементов
Дискретная
пространственная частота периодического по данной координате двумерного дискретного сигнала равна
отношению пространственного периода дискретизации по этой координате к пространственному периоду двумерного сигнала по этой же координате.
Обратное двумерное ДКП позволяет получить изображение в виде суммы двумерных дискретных гармонических функций
Слайд 19Основной принцип использования ДКП в современном цифровом телевидении
Входной дискретный сигнал
(одномерный или двумерный) подвергается прямому ДКП. Полученные коэффициенты обрабатываются. Выполняя
операции над коэффициентами ДКП мы, тем самым, выполняем операции над отдельными частотными составляющими сигнала.
В стандарте JPEG предусмотрено использование двух видов энтропийного кодирования: кодирование по Хаффману
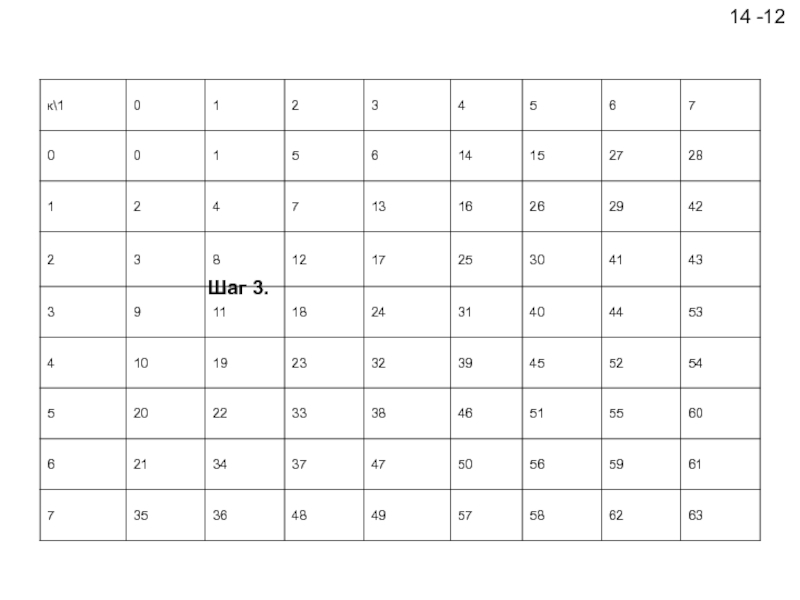
Перед выполнением энтропийного кодирования остальных 63 квантованных коэффициентов ДКП в каждом блоке выполняется следующая подготовительная операция. Двумерная матрица коэффициентов преобразуется в одномерную последовательность путем считывания ее элементов в зигзагообразном порядке, как показано в табл. 4.3.
Слайд 21Сжатие изображение в формат JPEG осуществляется в несколько этапов:
·
Преобразование цветового пространства
· Сегментация
· Дискретное косинусное преобразование
·
Квантование
· Кодирование
Декодирование JPEG осуществляется в обратном порядке.
Слайд 22ВЕДЕНИЕ В ВЕЙЛЕТ ПРЕОБРАЗОВАНИЕ
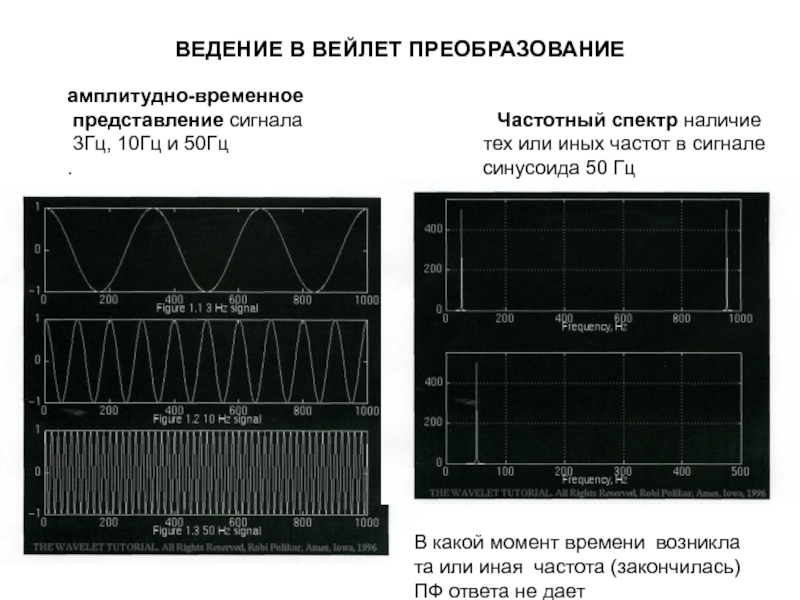
амплитудно-временное
представление сигнала
Частотный спектр наличие
3Гц, 10Гц и 50Гц тех или иных частот в сигнале
. синусоида 50 Гц
В какой момент времени возникла та или иная частота (закончилась) ПФ ответа не дает
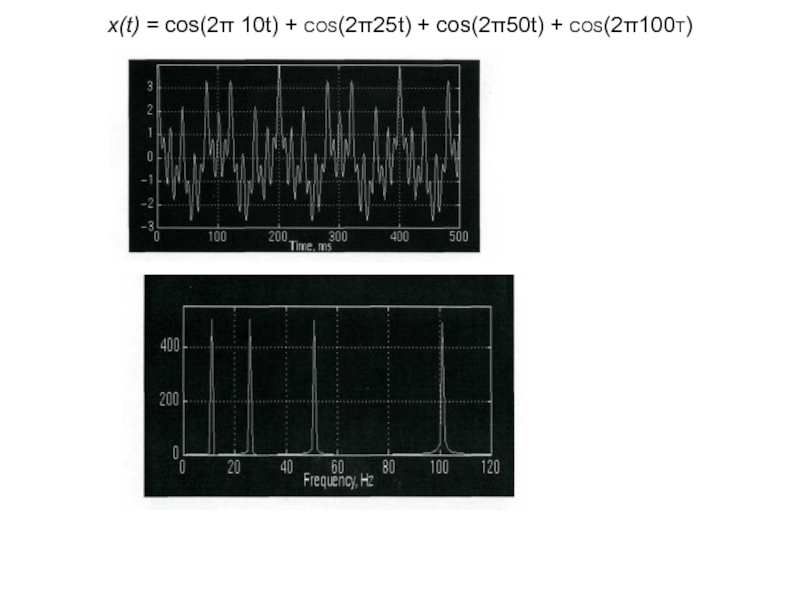
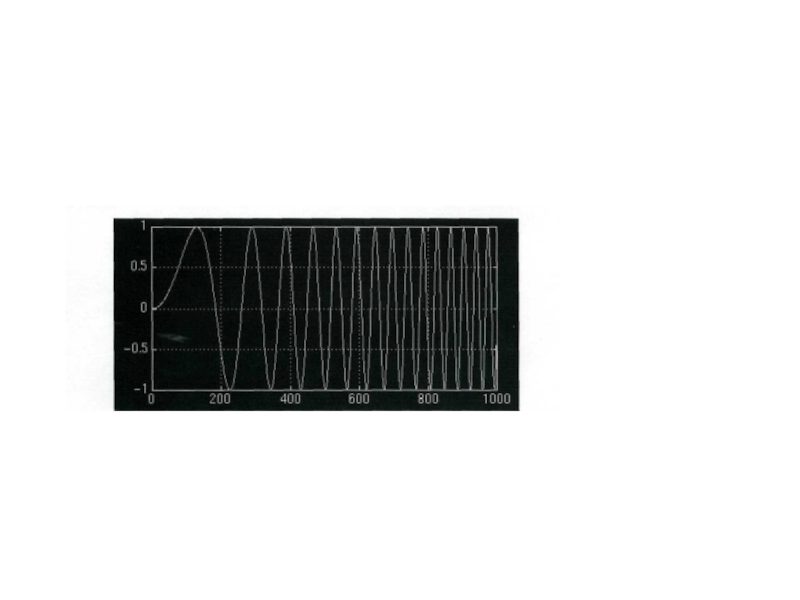
Слайд 23x(t) = cos(2π 10t) + cos(2π25t) + cos(2π50t) + cos(2π100t)
Слайд 24Для преобразования Фурье (FT) базисом являются функции wn(t), полученные из
функции
w(t) = e i t = cos t + i
sin t,
wn(t) = w(nt).
w(t) имеет период 2π.
FT широко используется для спектрального анализа
сигналов, однако имеет ряд недостатков
а) исходный сигнал заменяется на периодический, с периодом равным длительности исследуемого образца,
б) FT плохо работает при изменении параметров процесса со временем (нестационарности), поскольку дает усредненные коэффициенты для всего исследуемого образца
Слайд 26Проблемы ОПФ имеют свои корни в явлении, которое называется принципом
неопределенности Гейзенберга.
КМА позволяет получить хорошее разрешение по времени (плохое
по частоте) на высоких частотах и хорошее разрешение по частоте (плохое по времени) на низких частотах.
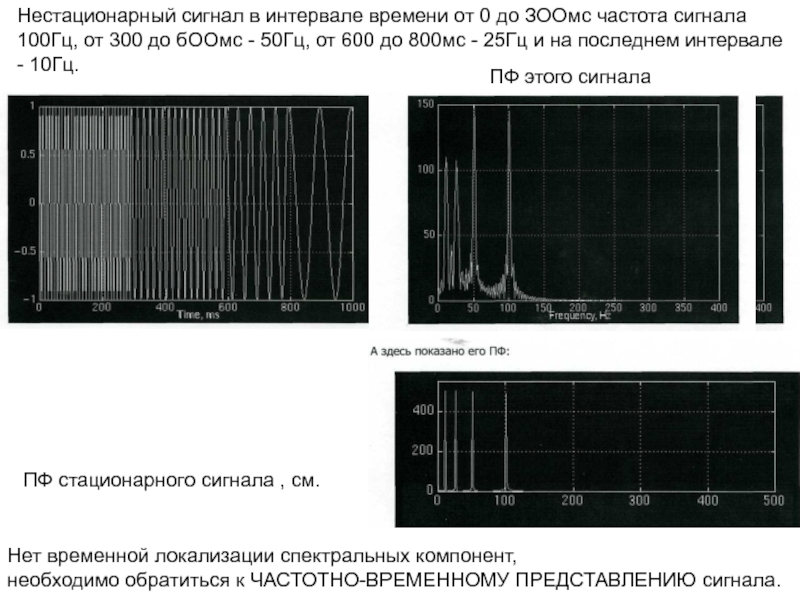
Слайд 27Нестационарный сигнал в интервале времени от 0 до ЗООмс частота
сигнала 100Гц, от 300 до бООмс - 50Гц, от 600
до 800мс - 25Гц и на последнем интервале - 10Гц.
ПФ этого сигнала
ПФ стационарного сигнала , см.
Нет временной локализации спектральных компонент,
необходимо обратиться к ЧАСТОТНО-ВРЕМЕННОМУ ПРЕДСТАВЛЕНИЮ сигнала.
Слайд 28WaveLet - Вейвлет
Вейвлеты - это обобщенное название семейств математических функций
определенной формы, которые локальны во времени и по частоте, и
в которых все функции получаются из одной базовой (порождающей) посредством ее сдвигов и растяжений по оси времени.
Вейвлет-преобразования (WT) подразделяют на дискретное (DWT) и непрерывное (CWT).
DWT используется для преобразований и кодирования сигналов, CWT - для анализа сигналов
Основная область применения вейвлет преобразований – анализ и обработка сигналов и функций, нестационарных во времени или неоднородных в пространстве, когда результаты анализа должны содержать не только частотную характеристику сигнала (распределение энергии сигнала по частотным составляющим), но и сведения о локальных координатах,
Слайд 29По сравнению с разложением сигналов на ряды Фурье, вейвлеты способны
с гораздо более высокой точностью представлять локальные особенности сигналов, вплоть
до разрывов 1-го рода (скачков).
В отличие от преобразований Фурье, вейвлет-преобразование одномерных сигналов обеспечивает двумерную развертку, при этом частота и координата рассматриваются как независимые переменные.
Базисная функция, вейвлет-функция – это некоторое "короткое" колебание, но не только. Понятие частоты спектрального анализа здесь заменено масштабом, и, чтобы перекрыть "короткими волнами" всю временную ось, введен сдвиг функций во времени
Слайд 30Определение вейвлета
К вейвлетам относятся локализованные функции, которые конструируются из одного
материнского вейвлета ψ(t) (или по любой другой независимой переменной) путем
операций сдвига), по аргументу (b) и масштабного изменения (а):
ψab(t) = (1 / ) ψ((t-b)/a (a, b)R, ψ(t)L2(R). где
множитель (1 / ) обеспечивает независимость нормы функций от масштабного числа 'a'.
Непрерывное вейвлет-преобразование сигнала
Дискретное вейвлет-преобразование сигнала
Слайд 31Непрерывное вейвлет-преобразование сигнала
НВПС s(t)L2(R), применяется для качественного частотно-временного анализа
по
смыслу соответствует преобразованию Фурье с заменой гармонического базиса
exp(-jωt )
на вейвлетный ψ ((t-b)/a):
С(a, b) = s(t), ψ ab(t)=(1/ )
s(t) ψ (t-b)/a) dt,
(a, b)R, a0.
Вейвлетный масштабно-временной спектр С(a,b) в отличие от фурье-спектра является функцией двух аргументов: масштаба вейвлета 'а' (в единицах, обратных частоте), и временного смещения вейвлета по сигналу 'b' (в единицах времени), при этом параметры 'а' и 'b' могут принимать любые значения в пределах областей их определения
Слайд 32преобразованный сигнал есть функция двух переменных,
(b) и (a),
параметры сдвига и масштаба, соответственно. функция преобразования, называющаяся материнским вейвлетом. ,
Параметр масштаба (a) ,в вейвлет-анализе имеет аналогию с масштабом географических карт. Большие значения масштаба (a) соответствуют малому количеству деталей, глобальному представлению сигнала, а низкие значения масштаба позволяют различить детали.
Аналогично, в терминах частоты, низкие частоты соответствуют глобальной информации о сигнале (которая содержится на всей его протяженности), а высокие частоты - детальной информации,
скрытым особенностям, которые имеют обычно малую протяженность.
Слайд 33Дискретное вейвлет-преобразование
Для входного сигнала, представленного массивом 2n чисел, вейвлет-преобразование Хаара
просто группирует элементы по 2 и образует от них суммы
и разности. Группировка сумм проводится рекурсивно (в случае чётной длины последовательности сумм) для образования следующего уровня разложения. В итоге получается 2n−1 разность и 1 общая сумма..
wavelet означает маленькая волна WT А. Хаар
Термин вейвлет-анализ по смыслу аналогичен термину Фурье-анализ. В обоих случаях речь идет о представлении исследуемого процесса в виде линейной комбинации различных функций, именуемых базисом соответствующего преобразования.
Слайд 34ДВП (DWT) -вейвлет-преобразования с заданием дискретных значений параметров (a,
b) вейвлетов с произвольным шагом Δa и Δb.
Дискретное вейвлет-преобразование
(ДВП) обеспечивает достаточно информации, как для анализа сигнала, так и для его синтеза, являясь вместе с тем экономным по числу операций и по требуемой памяти.
ДВП оперирует с дискретными значениями параметров а и b, которые задаются, как правило, в виде степенных функций:
b = k·ао-m, ao > 1, m, k I,
где I – пространство целых чисел {-, }, m – параметр масштаба, k – параметр сдвига.
Базис пространства L2(R) в дискретном представлении:
ymk(t) = |ао|m/2y(аоmt-k), m,k I, y(t) L2(R).
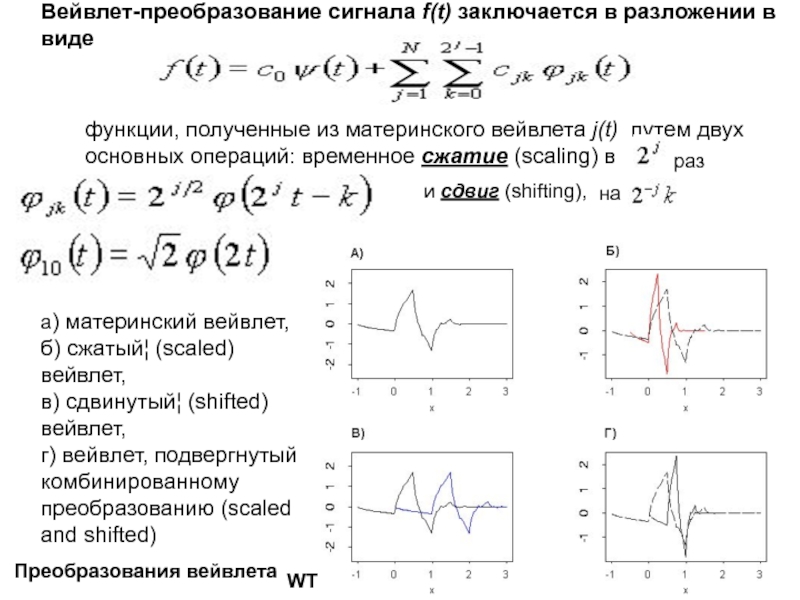
Слайд 35Вейвлет-преобразование сигнала f(t) заключается в разложении в виде
функции, полученные
из материнского вейвлета j(t) путем двух основных операций: временное сжатие
(scaling) в
и сдвиг (shifting),
раз
на
Преобразования вейвлета
WT
а) материнский вейвлет,
б) сжатый¦ (scaled) вейвлет,
в) сдвинутый¦ (shifted) вейвлет,
г) вейвлет, подвергнутый комбинированному преобразованию (scaled and shifted)
Слайд 36Вейвлет-коэффициенты прямого преобразования:
Cmk = s(t) ymk(t) dt.
Значение 'a'
может быть произвольным, но обычно принимается равным 2, при этом преобразование называется диадным вейвлет-преобразованием.
Для диадного преобразования разработан быстрый алгоритм вычислений, аналогичный быстрому преобразованию Фурье, что предопределило его широкое использование при анализе массивов цифровых данных.
Обратное дискретное преобразование для непрерывных сигналов при нормированном ортогональном вейвлетном базисе пространства:
s(t) = Cmk ymk(t).
выражение обратного вейвлет-преобразования
Слайд 37Типы вейвлетов
Вейвлеты могут быть ортогональнвми, полуортогональными, биортогональными. Вейвлетные функции
могут быть симметричными, несимметричными и асимметричными, с компактной областью определения
и не имеющие таковой, а также иметь различную степень гладкости
Для количественных методов анализа (декомпозиция сигналов с возможностью последующей линейной реконструкции сигналов из обработанных вейвлет-спектров) в качестве вейвлетных базисов можно использовать любые локализованные функции ψ(t), если для них существуют функции-двойники ψ #(t), такие, что семейства { ψ ab(t)} и { ψ #ab(t)} могут образовывать парные базисы функционального пространства, L2(R).
Вейвлеты, определенные таким образом, позволяют представить любую произвольную функцию в пространстве L2(R) в виде ряда:
s(t) = С(a,b) ψ #(ab(t), (a, b)I, где
коэффициенты С(a,b) – проекции сигнала на вейвлетный базис пространства, которые определяются скалярным произведением
С(a,b) = s(t), ψ ab(t) = s(t) ψ ab(t) dt.
Слайд 38
Если вейвлет ψ (t) обладает свойством ортогональности, то ψ
(t) ≡ ψ #(t) и
Вейвлет может быть неортогональным, однако,
если он имеет двойника, и пара (ψ(t), ψ # (t)) дает возможность сформировать семейства {ψmk(t)} и { ψ #zp(t)}, удовлетворяющие условию биортогональности на целых числах I:
Ψmk(t), Ψ#zp(t) = dmz·dkp, m,k,z,p I,
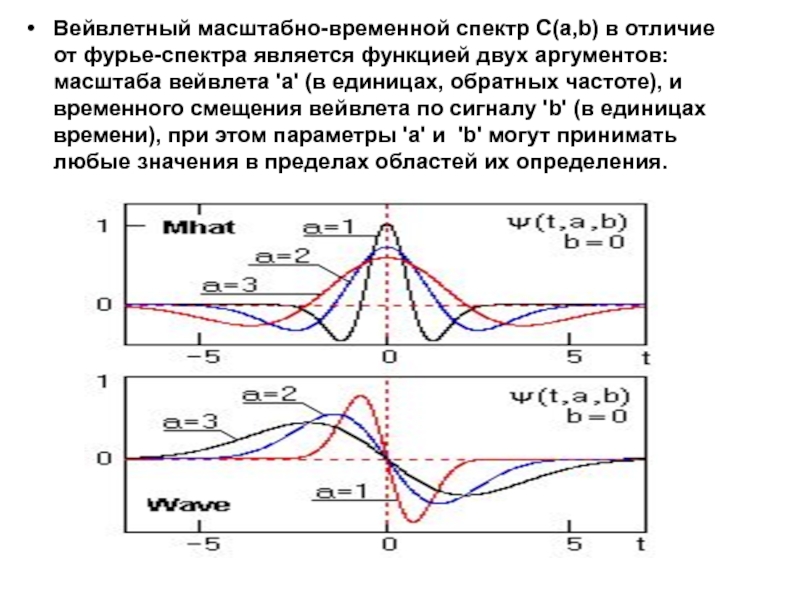
Слайд 39Вейвлетный масштабно-временной спектр С(a,b) в отличие от фурье-спектра является функцией
двух аргументов: масштаба вейвлета 'а' (в единицах, обратных частоте), и
временного смещения вейвлета по сигналу 'b' (в единицах времени), при этом параметры 'а' и 'b' могут принимать любые значения в пределах областей их определения.
Слайд 40Вейвлет-преобразование (WT) в большой степени позволяет преодолеть перечисленные недостатки FT,
поскольку базисные функции WT обладают свойством временной локализации,
обладают конечной
энергией (нормой):
Часто используемые вейвлеты: (а)WAVE, (б)MHAT - мексиканская шляпа, (в) Morlet - Морле, (г)Paul - Пауля, (д) LMB, (е)Daubechies - Добечи. Вейвлеты (в) и (г) являются комплексными.
Временное представление некоторых вейвлетов и соответствующие им Фурье-образы.
Симметричеые , несимметричные
Униполярные , биполярные
Неортогональные, ортогональные,
Биортогональные,
Слайд 41Свойства вейвлета
Вейвлет должен быть непрерывным, интегрируемым, иметь компактный носитель и
быть локализованным как во времени (в пространстве), так и по
частоте.
Если вейвлет в пространстве сужается, то его "средняя" частота повышается, спектр вейвлета перемещается в область более высоких частот и расширяется. Этот процесс должен быть линейным – сужение вейвлета вдвое должно повышать его "среднюю" частоту и ширину спектра также вдвое.
Нулевое среднее значение, т.е. выполнение условия для нулевого момента: y(t) dt = 0,
Ограниченность. Необходимое и достаточное условие: ||y(t)||2 = |y(t)|2 dt <
Автомодельность базиса или самоподобие
Слайд 42Отображение преобразования
Результатом вейвлет-преобразования одномерного числового ряда (сигнала) является :
двумерный массив значений коэффициентов С(a,b)
Распределение этих значений в пространстве
(a,b) - временной масштаб, временная локализация, дает информацию об изменении во времени относительного вклада в сигнале вейвлетных компонент разного масштаба и называется спектром коэффициентов вейвлет-преобразования, масштабно-временным (частотно-временным) спектром или просто вейвлет-спектром (wavelet spectrum).
. Спектр C(a,b) одномерного сигнала представляет собой поверхность в трехмерном пространстве. Способы визуализации спектра могут быть самыми различными.
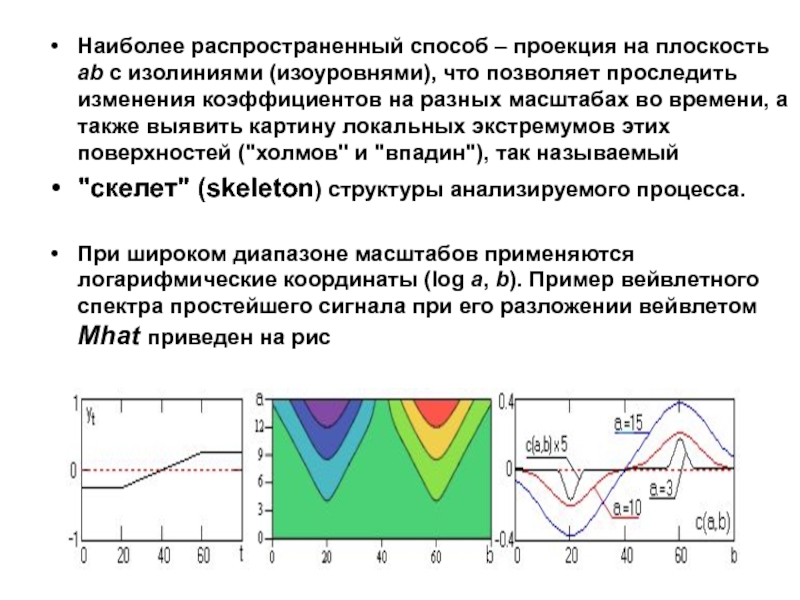
Слайд 43Наиболее распространенный способ – проекция на плоскость ab с изолиниями
(изоуровнями), что позволяет проследить изменения коэффициентов на разных масштабах во
времени, а также выявить картину локальных экстремумов этих поверхностей ("холмов" и "впадин"), так называемый
"скелет" (skeleton) структуры анализируемого процесса.
При широком диапазоне масштабов применяются логарифмические координаты (log a, b). Пример вейвлетного спектра простейшего сигнала при его разложении вейвлетом Mhat приведен на рис
Слайд 44По вертикальным сечениям (сечениям сдвига b) вейвлет-спектр отражает компонентный состав
сигнала (из данного комплекта вейвлетов) в каждый текущий момент.
По
смыслу преобразования, как скалярного произведения сигнала с вейвлетом, ясно, что значения коэффициентов в каждой текущей временной точке по масштабным сечениям тем больше, чем сильнее корреляция между вейвлетом данного масштаба и поведением сигнала в окрестностях этой точки. Соответственно, сечения по параметру 'а' демонстрируют изменения в сигнале компоненты данного масштаба 'a' со временем.
Слайд 45Свойства вейвлет-преобразования
Результаты вейвлет-преобразования, как скалярного произведения вейвлета и сигнальной
функции, содержат комбинированную информацию об анализируемом сигнале и самом вейвлете.
Линейность.
TW[a·s1(t)+b·s2(t)] = a·TW[s1(t)]+b·TW[s2(t)].
Инвариантность относительно сдвига.
TW[s(t/аo)] = (1/ао)·C(a/ао,b/аo).
Инвариантность относительно масштабирования
TW[s(t/аo)] = (1/ао)·C(a/ао,b/аo).
Дифференцирование
dn{TW[s(t)]}/dtn = TW[dn(s(t))/dtn].
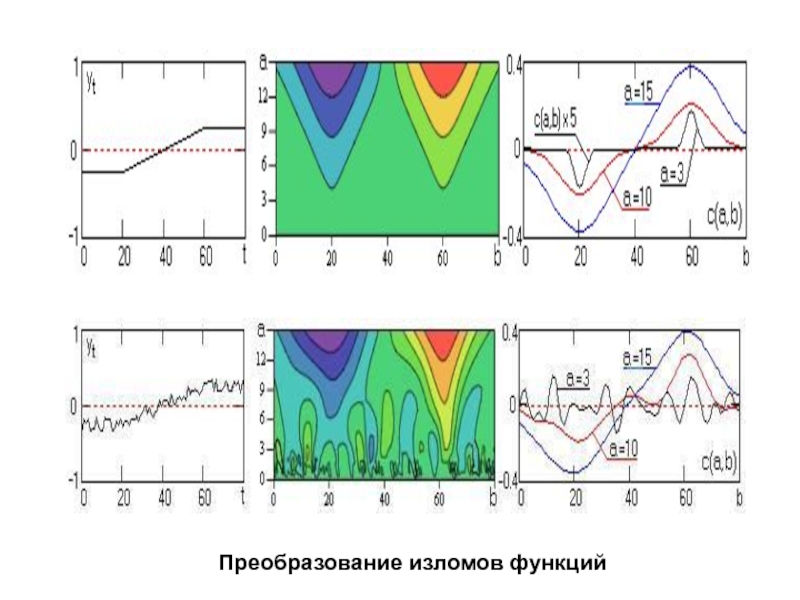
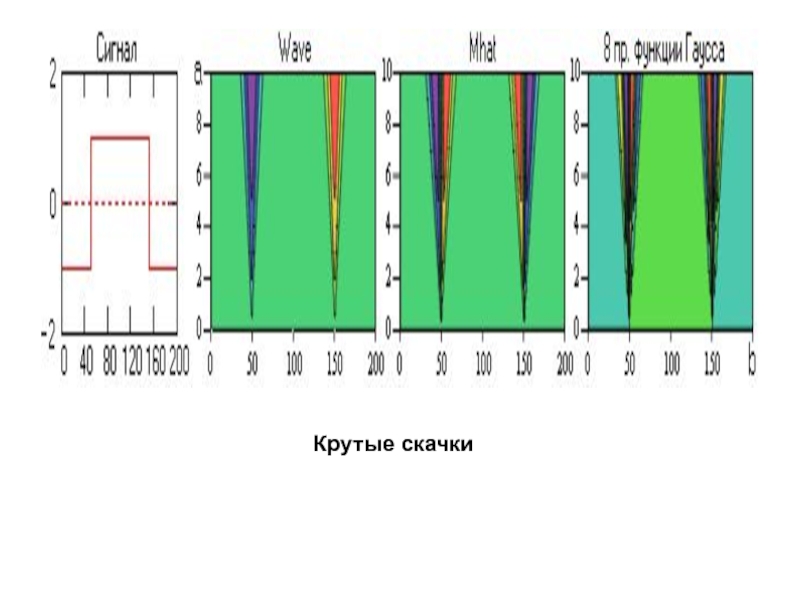
Слайд 46При анализе сигналов вейвлетами четного типа (симметричными или близкими к
симметричным) гармоническим сигналам обычно соответствуют яркие горизонтальные полосы вейвлетных пиков
и впадин на доминирующих частотах вейвлетов, совпадающих с частотой гармоник сигналов.
Нарушения гладкости сигналов фиксируются вертикальными полосами, пики в сигналах выделяются максимумами, а впадины – минимумами вейвлетных коэффициентов.
Напротив, вейвлеты нечетного типа более резко реагируют на скачки и быстрые изменения в сигналах, отмечая их максимумами или минимумами в зависимости от знака дифференциалов. Чем резче выражены особенности сигналов, тем сильнее они выделяются на спектрограммах.
Для конструирования таких вейвлетов часто используются производные функции Гаусса, которые имеют наилучшую локализацию как во временной, так и в частотной областях
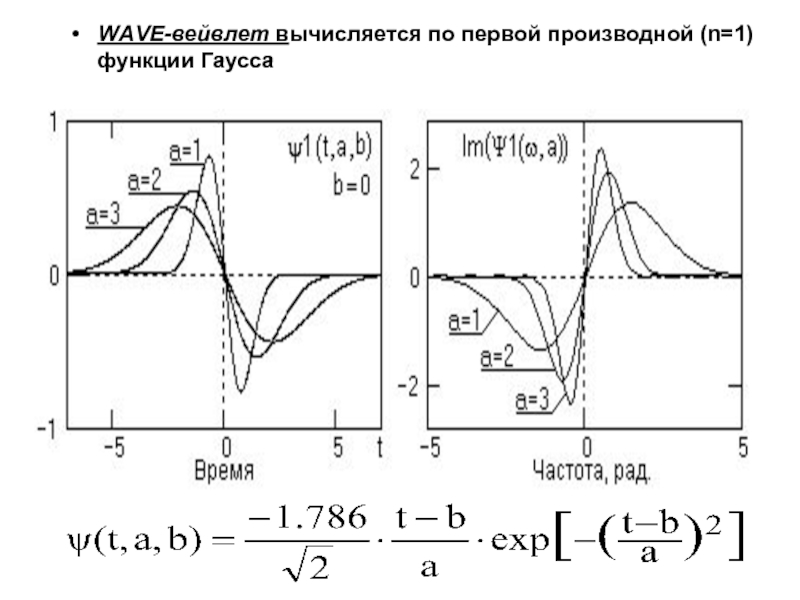
Слайд 47WАVE-вейвлет вычисляется по первой производной (n=1) функции Гаусса
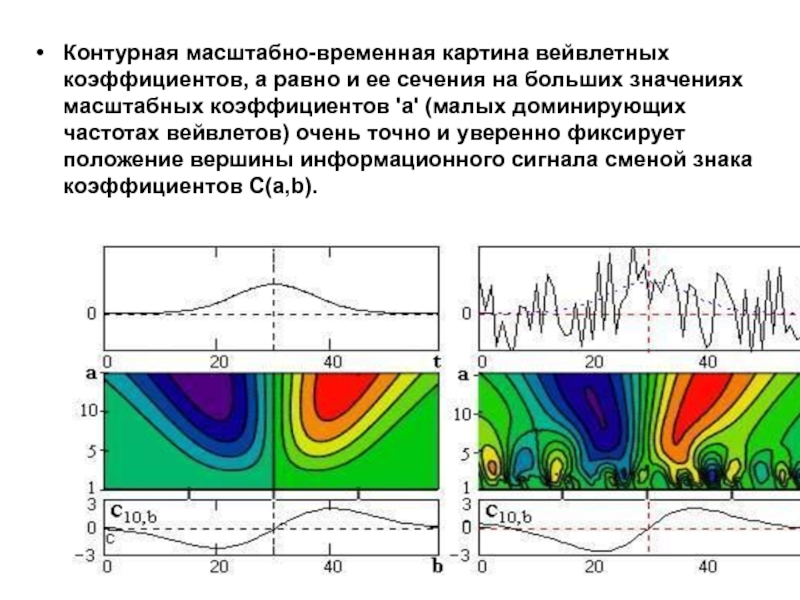
Слайд 48Контурная масштабно-временная картина вейвлетных коэффициентов, а равно и ее сечения
на больших значениях масштабных коэффициентов 'а' (малых доминирующих частотах вейвлетов)
очень точно и уверенно фиксирует положение вершины информационного сигнала сменой знака коэффициентов С(a,b).
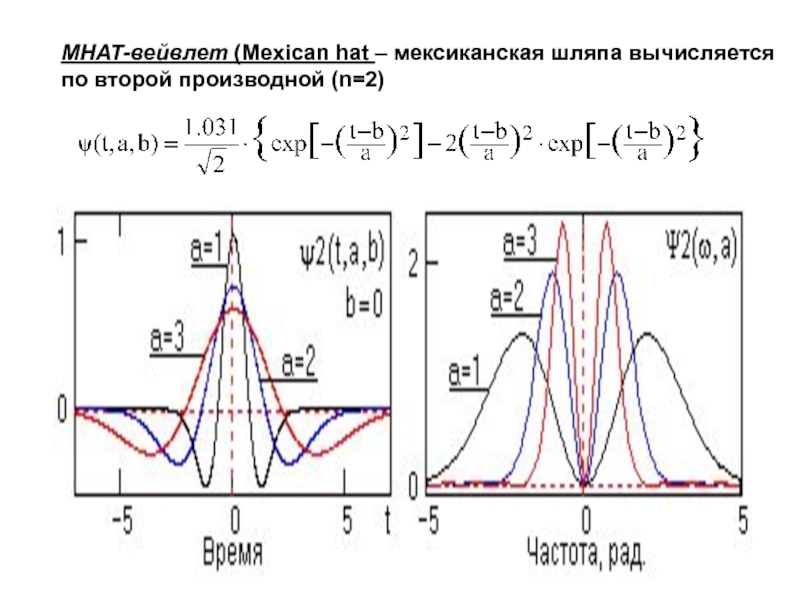
Слайд 49МНАТ-вейвлет (Mexican hat – мексиканская шляпа вычисляется по второй производной
(n=2)
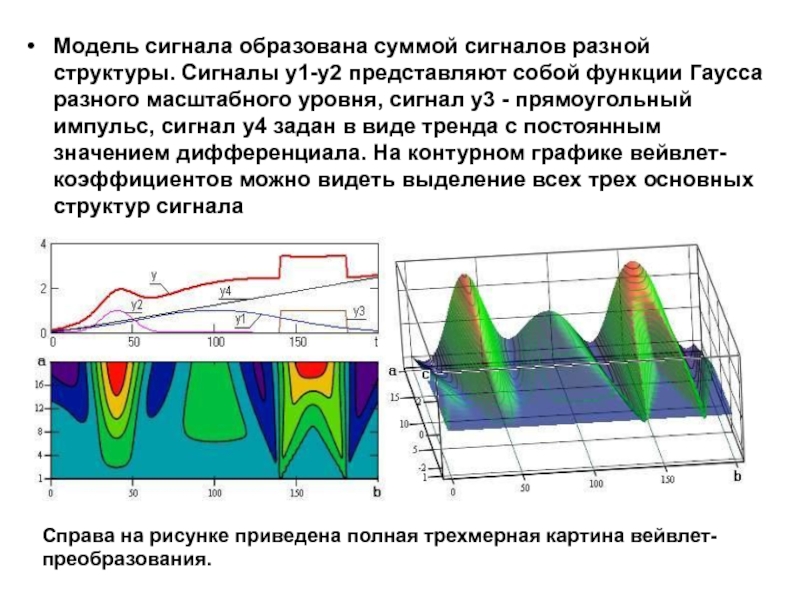
Слайд 50Модель сигнала образована суммой сигналов разной структуры. Сигналы у1-у2 представляют
собой функции Гаусса разного масштабного уровня, сигнал у3 - прямоугольный
импульс, сигнал у4 задан в виде тренда с постоянным значением дифференциала. На контурном графике вейвлет-коэффициентов можно видеть выделение всех трех основных структур сигнала
Справа на рисунке приведена полная трехмерная картина вейвлет-преобразования.
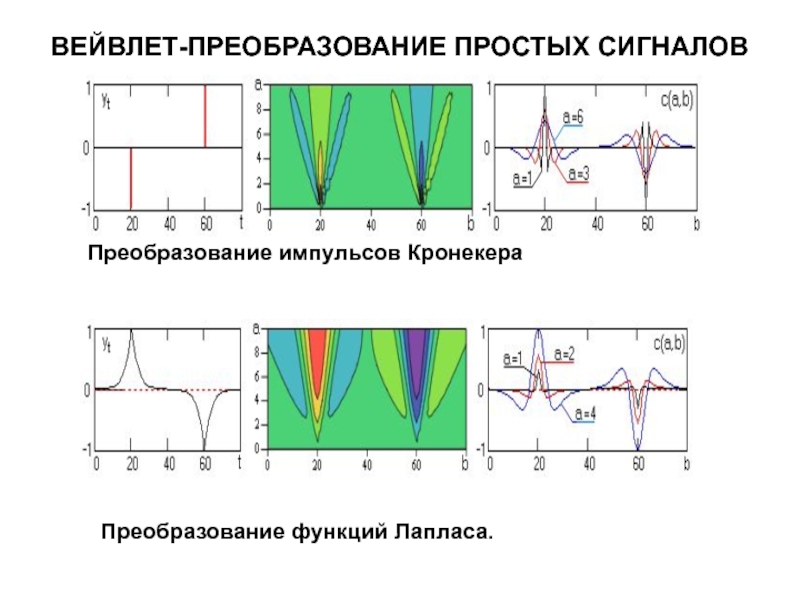
Слайд 51Вейвлет-преобразование простых сигналов
Преобразование импульсов Кронекера
Преобразование функций Лапласа.
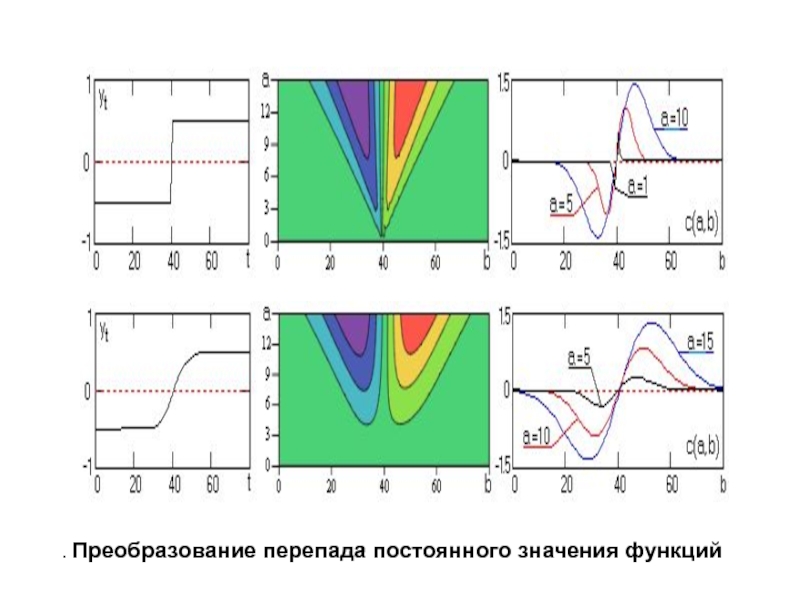
Слайд 52. Преобразование перепада постоянного значения функций
Слайд 55Применение вейвлтов
Обработка экспериментальных данных.
Поскольку вейвлеты появились именно как механизм
обработки экспериментальных данных, их применение для решения подобных задач представляется
весьма привлекательным до сих пор. Вейвлет-преобразование дает наиболее наглядную и информативную картину результатов эксперимента, позволяет очистить исходные данные от шумов и случайных искажений, и даже "на глаз" подметить некоторые особенности данных и направление их дальнейшей обработки и анализа
Вейвлеты хорошо подходят для анализа нестационарных сигналов, возникающих в медицине, анализе фондовых рынков и других областях.
Слайд 56 Обработка изображений
Используя вейвлет-преобразование, мы можем сгладить или
выделить некоторые детали изображения, увеличить или уменьшить его, выделить важные
детали и даже повысить его качество!
Сжатие данных
Особенностью ортогонального многомасштабного анализа является то, что для достаточно гладких данных полученные в результате преобразования детали в основном близки по величине к нулю и, следовательно, очень хорошо сжимаются обычными статистическими методами.
Достоинством ВП является то, что оно не вносит дополнительной избыточности в исходные данные, и сигнал может быть полностью восстановлен с использованием тех же самых фильтров.
Изображение, обработанное вейвлетами, можно сжать в 3-10 раз без существенных потерь информации (а с допустимыми потерями – до 300 раз!).
Слайд 57Фильтрация сигналов
При больших коэффициентах сжатия JPEG дает блочные искажения, являющиеся
следствием используемого алгоритма ДКП
Слайд 5814 -19
Идея применения вейвлетов для многомасштабного анализа заключается в том,
что разложение сигнала производится по базису, образованному сдвигами и разномасштабными
копиями функции-прототипа
(то есть вейвлет-преобразование по своей сути является фрактальным).
Пример многомасштабного анализа изображения
Вычислительная процедура дискретного WT (DWT) состоит в вычислении временной свертки сигнала с {φjk(t)}
Длина вейвлета для каждого последующего масштаба уменьшается в 2 раза. Для DWT используется вычислительная процедура быстрого преобразования
Для масштаба j=1 определяется 2 коэффициента: c10 и c11 , для j=2 - 4 коэффициента и т.д., поэтому вычислительный алгоритм DWT называют пирамидальным алгоритмом.
Слайд 5914 -21
Кроме того, отделение в результате преобразования деталей от основного
сигнала позволяет очень просто реализовать сжатие с потерями – достаточно
просто отбросить детали на тех масштабах, где они несущественны!
Изображение, обработанное вейвлетами, можно сжать в 3-10 раз без существенных потерь информации (а с допустимыми потерями – до 300 раз!).
Вейвлет-преобразование положено в основу стандарта сжатия данных MPEG4.
а) б) в)
Слайд 60сигнал перемножается с функцией (вейвлетом), также как и с оконной
функцией при ОПФ, и преобразование выполняется раздельно для разных участков
времени сигнала.
Однако существует две существенные разности между ОПФ и НВП:
Ширина окна изменяется, так что преобразование вычисляется для каждой спектральной компоненты, что является наиболее важным свойством вейвлет-преобразования.
Непрерывное вейвлет-преобразование определяется следующим образом Как видно из равенства, преобразованный сигнал есть функция двух переменных, tau и s, параметры сдвига и масштаба Слово вейвлет означает маленькая волна. Под маленькой понимается то, что эта функция (окно) имеет конечную ширину (компактный носитель).
Слово «волна» отражает тот факт, что вейвлет-функция осциллирует. Термин «материнский» означает, что функции с различной шириной носителя, используемые в преобразовании, порождаются одной базовой функцией - материнским вейвлетом.
Масштаб определяется как величина, обратную частоте.
Слайд 6114 -1
Термин сдвиг используется здесь в том же смысле, что
и при ПФ: он относится к местоположению окна, и окно
движется вдоль сигнала. Этот термин относится, таким образом, к временной информации, присутствующей в результате преобразования.
Однако при ВП мы не имеем частотного параметра, как это было при ОПФ. Вместо него здесь имеется параметр масштаба, который можно определить как величину, обратную частоте. Понятие масштаба более подробно объясняется в дальнейшем.
Однако в определении вейвлет-преобразования коэффициент масштаба стоит в знаменателе. Поэтому, s > 1 расширяет сигнал, a s < 1 сжимает его.
Слайд 62.
Однако в определении вейвлет-преобразования коэффициент масштаба стоит в знаменателе. Поэтому,
s > 1 расширяет сигнал, a s < 1 сжимает
его.
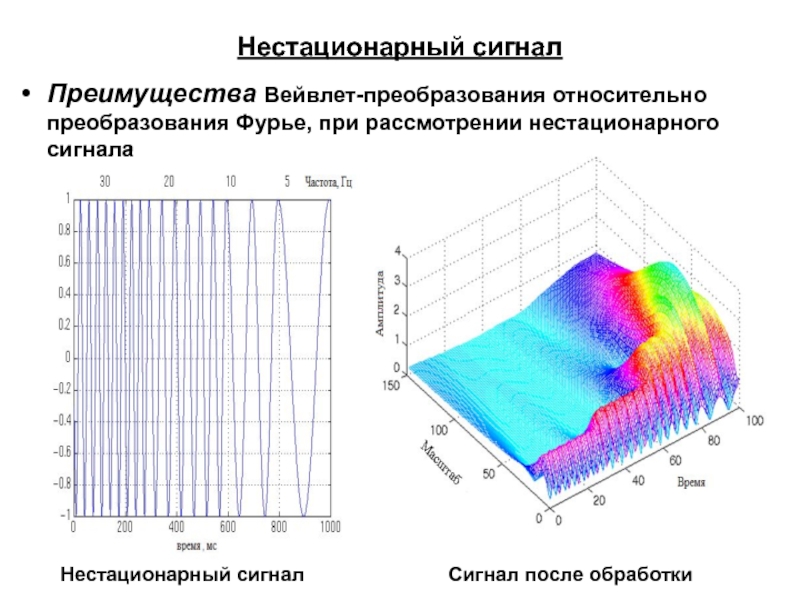
Слайд 63Нестационарный сигнал
Преимущества Вейвлет-преобразования относительно преобразования Фурье, при рассмотрении нестационарного сигнала
Нестационарный сигнал
Сигнал после обработки
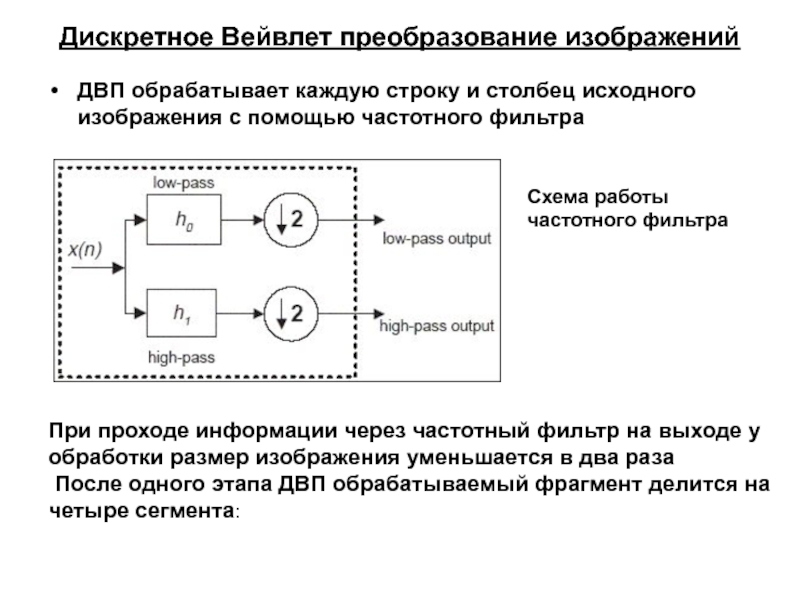
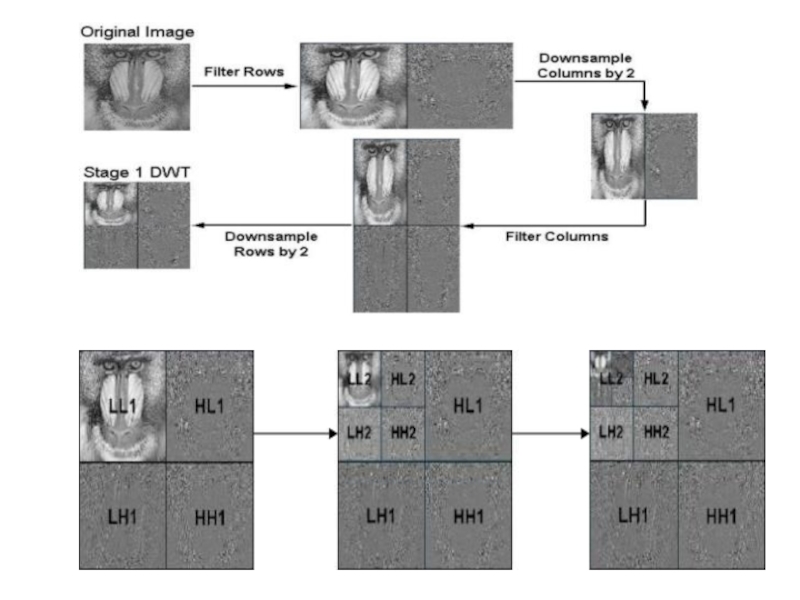
Слайд 64Дискретное Вейвлет преобразование изображений
ДВП обрабатывает каждую строку и столбец исходного
изображения с помощью частотного фильтра
Схема работы частотного фильтра
При проходе информации
через частотный фильтр на выходе у обработки размер изображения уменьшается в два раза
После одного этапа ДВП обрабатываемый фрагмент делится на четыре сегмента:
Слайд 66Методы оценки качества изображений
(PSNR) пиковое отношение сигнал-шум
(MSE), среднеквадратическая ошибка
Коэффициент сжатия изображения
Мера потерянного объема информации
Метрика SSIM
SSIM рассматривают деградацию
изображения как воспринятое изменение в структурной информации
Идея заключается в том, что пиксели имеют сильную взаимосвязь, особенно когда они близки пространственно. формула применима только для яркости изображения, по которой и происходит оценка качества.
Метрика SSIM вычислена на различные окна изображения. Мера между двумя окнами x и y общего размера N×N
Слайд 67(SSIM) является методом измерения подобия между двумя изображениями (Индекс структурного
подобия (SSIM) метод учитывает "восприятие ошибки", благодаря учёту структурного изменения
информации. · - среднее x;
·
Слайд 68Коэффициент сжатия изображения
Коэффициент сжатия изображения вычисляется как отношение информационных энтропий
по Шеннону для исходного изображения, и изображения, реконструированного после преобразования
Информационная
энтропия вычисляется по формуле
где р – вероятность появления каждого значения пиксела, вычисляется как отношение суммарного числа появлений каждого значения пиксела к общему числу пикселов (размер изображения
Слайд 69отношения сигнал/шум -
среднеквадратичная погрешность (mean square error) -