и обработки данных»
Студент группы Ф7-12-5 Носиров Тулкинжон
Национальный исследовательский технологический
университет Московский институт стали и сплавов
Кафедра инженерной кибернетики


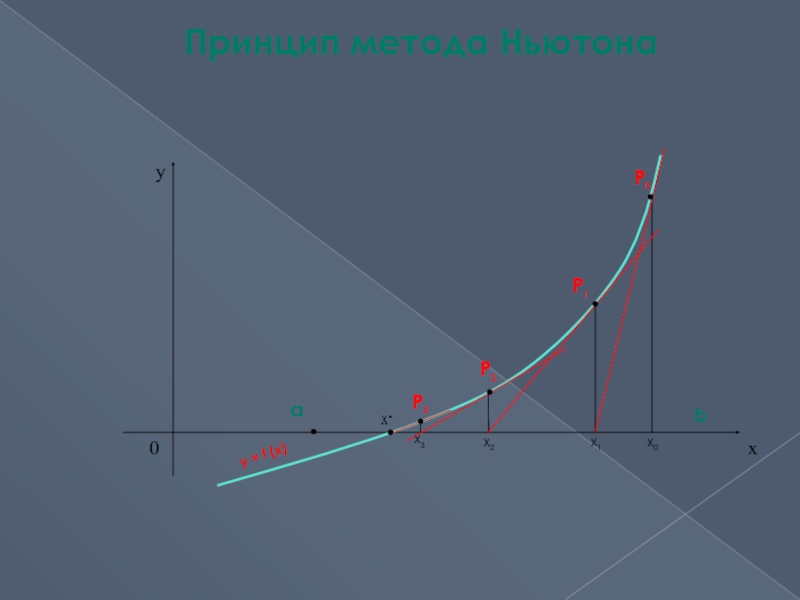
![Применение программных средств для анализа и обработки данных Описание метода НьютонаВыберем на отрезке [a, b] некоторую точку х0 и Описание метода НьютонаВыберем на отрезке [a, b] некоторую точку х0 и проведем в точке P0(х0, f(х0)) графика](/img/thumbs/7d1844c56d397d8ef6c0f8d4ff1ad7c5-800x.jpg)