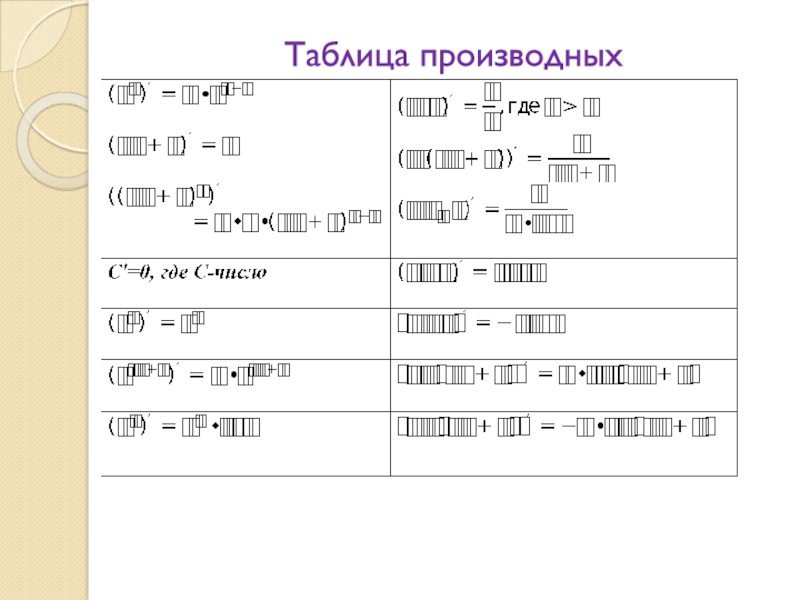
Слайд 1Применение производной к исследованию функций.
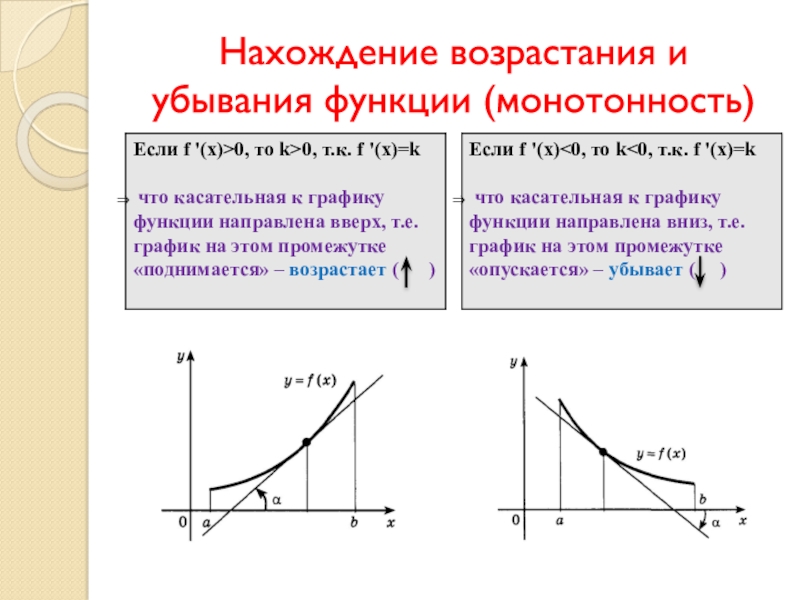
Слайд 3Нахождение возрастания и убывания функции (монотонность)
Слайд 4Теорема
Итак, если f '(x)>0 на промежутке, то функция f(x) возрастает
на этом промежутке.
Если f '(x)
убывает на этом промежутке.
Задача
Найти интервалы монотонности функции f(x)= x3-3x2
ООФ x- любое
f '(x)=(x3-3x2)'=3x2-3∙2x=3x2-6x
f '(x)=0 3x2-6x=0
3x(x-2)=0
x=0 x=2 – стационарные точки
4. + - + f '(x)
0 2 f(x)
5. x<0, x>2 –функция возрастает
0
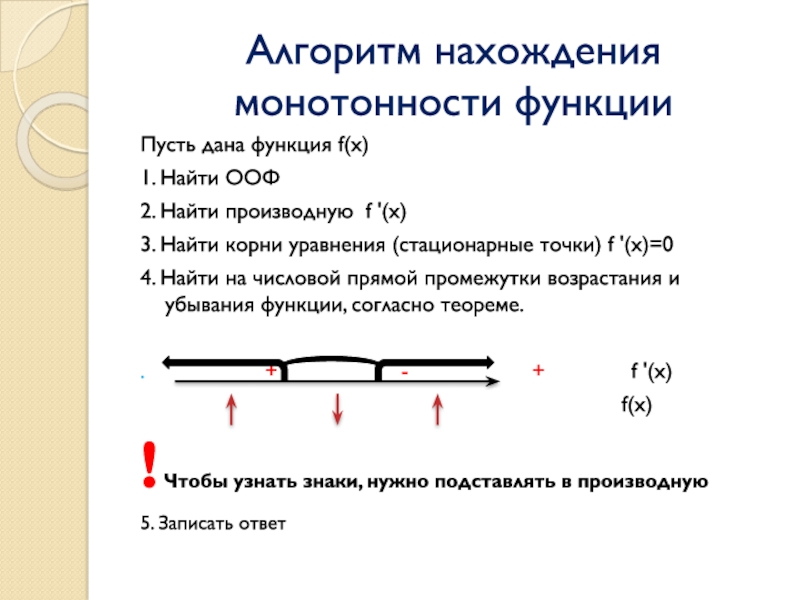
Слайд 5Алгоритм нахождения монотонности функции
Пусть дана функция f(x)
1. Найти ООФ
2. Найти
производную f '(x)
3. Найти корни уравнения (стационарные точки) f '(x)=0
4.
Найти на числовой прямой промежутки возрастания и убывания функции, согласно теореме.
. + - + f '(x)
f(x)
! Чтобы узнать знаки, нужно подставлять в производную
5. Записать ответ
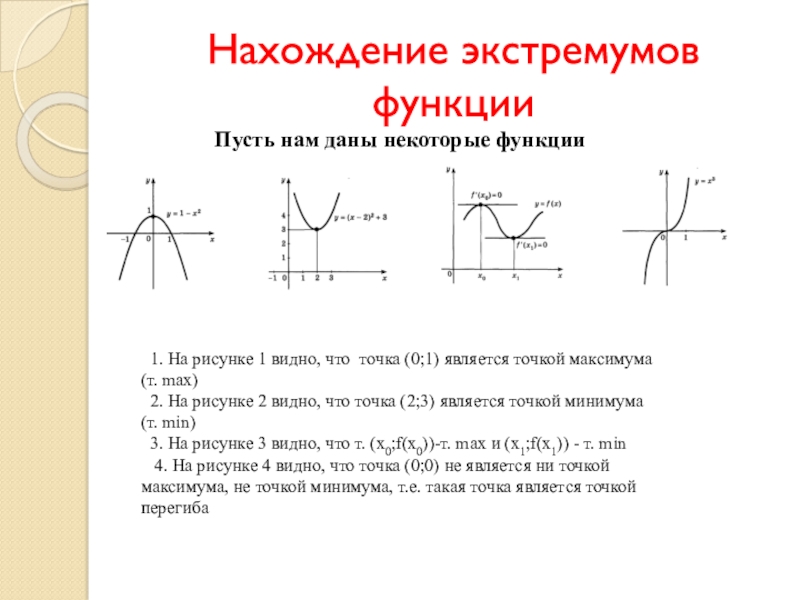
Слайд 6Нахождение экстремумов функции
Слайд 7Основные определения
О1: Точка x0 называется точкой максимума функции f(x), если
существует такая окрестность точки x0, что для всех x≠ x0
из этой окрестности выполняется неравенство
f(x)О2: Точка x0 называется точкой минимума функции f(x), если существует такая окрестность точки x0, что для всех x≠ x0 из этой окрестности выполняется неравенство
f(x)>f(x0)
О3: Точки максимума и минимума называются точками экстремума
ТЕОРЕМА
Если x0 – точка экстремума дифференцируемой функции f(x), то
f '(x0)=0
Слайд 8Задача
Найти точки экстремума функции f(x)=x4-4x3
ООФ x-любое
f '(x)=(x4-4x3)’ =4x3-4∙3x2= 4x3-12x2
f '(x)=0
4x3-12x2=0
4x2(x-3)=0
x=0 x=3 – стационарные точки
4.
- - + f '(x)
0 3 f(x)
5. x=3 – точка min ( )
x=0 – точка перегиба (т.к. производная в этой точке свой знак не меняет)
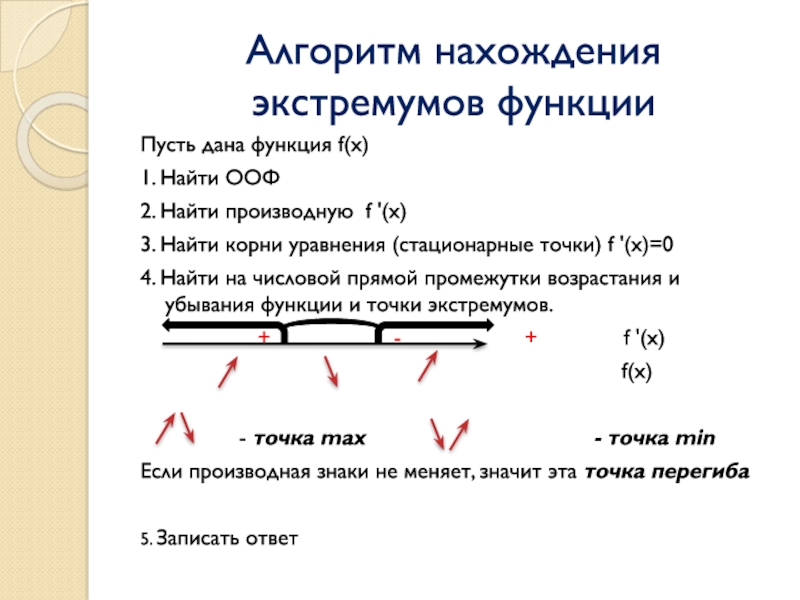
Слайд 9Алгоритм нахождения экстремумов функции
Пусть дана функция f(x)
1. Найти ООФ
2. Найти
производную f '(x)
3. Найти корни уравнения (стационарные точки) f '(x)=0
4.
Найти на числовой прямой промежутки возрастания и убывания функции и точки экстремумов.
+ - + f '(x)
f(x)
- точка max - точка min
Если производная знаки не меняет, значит эта точка перегиба
5. Записать ответ
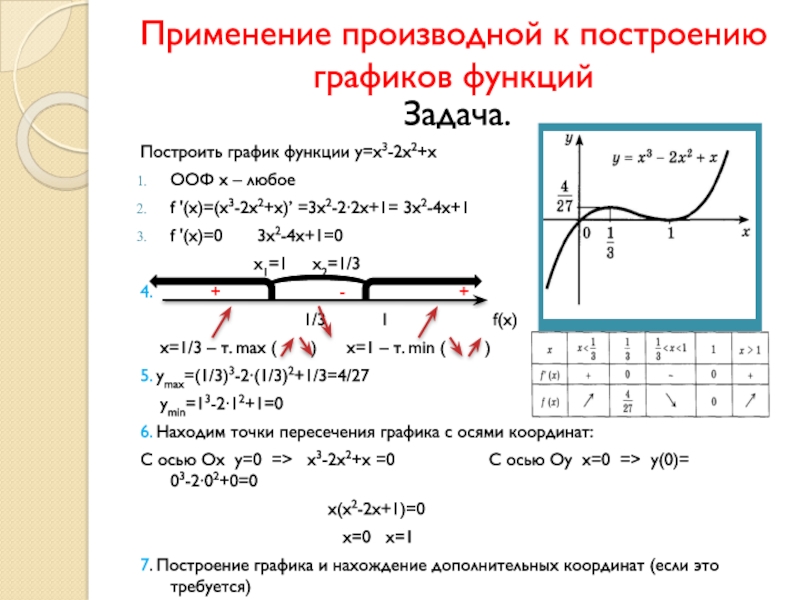
Слайд 10Применение производной к построению графиков функций
Задача.
Построить график функции y=x3-2x2+x
ООФ x – любое
f '(x)=(x3-2x2+x)’ =3x2-2∙2x+1= 3x2-4x+1
f '(x)=0
3x2-4x+1=0
x1=1 x2=1/3
4. + - + f '(x)
1/3 1 f(x)
x=1/3 – т. max ( ) x=1 – т. min ( )
5. ymax=(1/3)3-2∙(1/3)2+1/3=4/27
ymin=13-2∙12+1=0
6. Находим точки пересечения графика с осями координат:
С осью Ох у=0 => x3-2x2+x =0 С осью Оу х=0 => у(0)= 03-2∙02+0=0
х(х2-2х+1)=0
х=0 х=1
7. Построение графика и нахождение дополнительных координат (если это требуется)
Слайд 11Алгоритм для построения графиков функций
Пусть дана функция f(x)
1. Найти ООФ
2.
Найти производную f '(x)
3. Найти корни уравнения (стационарные точки) f
'(x)=0
4. Найти на числовой прямой точки экстремума.
+ - + f '(x)
f(x)
- точка max - точка min
Если производная знаки не меняет, значит эта точка перегиба
5. Значение функции в этих точках, т. е. ymax и ymin ( подставлять в f(x))
6. Нахождение точек пересечения графика с осями координат
С осью Ох у=0, т.е. f(x)=0 С осью Оу х=0, т.е. у(0)
7. Построение графика и нахождение дополнительных координат (если это требуется)