Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Принципы механики. принцип возможных перемещений
Содержание
- 1. Принципы механики. принцип возможных перемещений
- 2. Классификация связей.Принцип возможных перемещений (Принцип Лагранжа).Общее уравнение
- 3. КЛАССИФИКАЦИЯ СВЯЗЕЙ.1. Связи делятся на стационарные и
- 4. 2. Связи делятся на геометрические и кинематические
- 5. По виду связей механические системы тоже разделяются
- 6. Задание 23Варианты ответаУкажите правильный вариант характеристик связей
- 7. Действие связей можно учитывать не только вводя
- 8. Возможное перемещение точки отличается от действительного прежде
- 9. В общем случае система может иметь множество
- 10. Через них можно выразить любой радиус –
- 11. Возможная работа активной силы
- 12. Опр. Идеальными называются связи, для которых элементарная
- 13. Примечание. Скользящая заделка - это заделка, которая
- 14. Перемещения
- 15. Поделим уравнение (1) на δs ≠ 0
- 16. Следовательно,
- 17. С) Найдем момент пары сил, возникающей в
- 18. Двойная скользящая заделка – связь которая допускает
- 19. 3. Составим уравнение возможных работ (1). ΣδМk =
- 20. Примечание 2. В качестве моментной точки в
- 21. Задача. Вес бревна Q, вес каждого из
- 22. 2.Сообщим системе возможное перемещениеδsС = δsС1=δsС2 –
- 23. Если ко всем точкам системы кроме действующих
- 24. Так как на систему наложены идеальные связи,
- 25. Пример применения принцип Даламбера – Лагранжа.В подъемнике
- 26. 2. Присоединим к ним силу инерции груза
- 27. Окончательно уравнение движения примет вид4. Входящие сюда величины выразим через искомое В результате найдем окончательно
- 28. Задание 25Варианты ответа1) 15 м/с2 2) 20 м/с2
- 29. Задание 26Варианты ответа1) 17 Нм 2) 11 Нм
- 30. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Принципы механики.
ДИНАМИКА механической системы и твердого тела.
Принцип возможных перемещений.
Слайд 2Классификация связей.
Принцип возможных перемещений (Принцип Лагранжа).
Общее уравнение динамики (Принцип Даламбера
-Лагранжа)
Возможные перемещения системы. Число степеней свободы.
Пример применения принципа возможных перемещений
(Задание Д6). ВОПРОСЫ ТЕМЫ
Слайд 3КЛАССИФИКАЦИЯ СВЯЗЕЙ.
1. Связи делятся на стационарные и нестационарные.
Опр. Связями называются
любого вида ограничения, которые налагаются на положения и скорости точек
механической системы и выполняются независимо от того, какие на систему действуют заданные силы.Опр. Связи, не изменяющиеся со времени, называются стационарными, а изменяющиеся со временем – нестационарными.
Слайд 42. Связи делятся на геометрические и кинематические (дифференциальными).
Опр. Связи, налагающие
ограничения на положение (координаты) точек системы, называются геометрическими, а налагающие
ограничения еще и на скорости (первые производные от координат по времени) точек системы – кинематическими или дифференциальными.3. Связи делятся на интегрируемые и неинтегрируемые.
Опр. Если дифференциальную связи можно представить как геометрическую, т. е. устанавливаемую этой связью зависимость между скоростями свести к зависимости между координатами, то такая связь называется интегрируемой, а в противном случае – неинтегрируемой.
Слайд 5По виду связей механические системы тоже разделяются на голономные (с
голономными связями) и неголономные (содержащие неголономные связи).
4. Связи делятся на
голономные и неголономные.Опр. Геометрические и интегрируемые дифференциальные связи называются связями голономными, а неинтегрируемые дифференциальные связи – неголономными.
5. Связи делятся на удерживающие и неудерживающие.
Опр. Удерживающими связями называются связи, которые накладывают ограничения, сохраняющиеся при любом положении системы, неудерживающимися – связи, которые этими свойствами не обладают (от таких связей система может «освобождаться»).
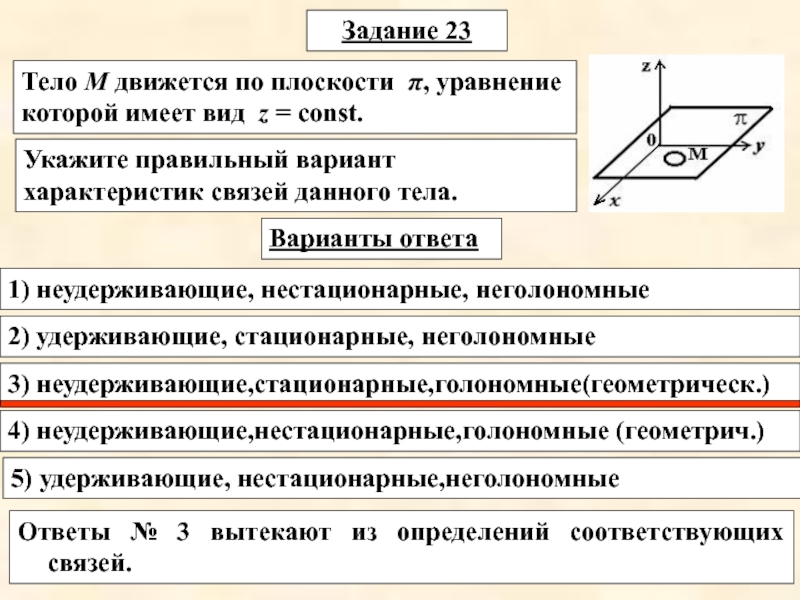
Слайд 6Задание 23
Варианты ответа
Укажите правильный вариант характеристик связей данного тела.
Тело
М движется по плоскости π, уравнение которой имеет вид z
= const.Ответы № 3 вытекают из определений соответствующих связей.
1) неудерживающие, нестационарные, неголономные
2) удерживающие, стационарные, неголономные
3) неудерживающие,стационарные,голономные(геометрическ.)
4) неудерживающие,нестационарные,голономные (геометрич.)
5) удерживающие, нестационарные,неголономные
Слайд 7Действие связей можно учитывать не только вводя их реакции, но
и рассматривая перемещения, которые точки механической системы могут иметь при
наложенных на нее связях.ВОЗМОЖНЫЕ ПЕРЕМЕЩЕНИЯ СИСТЕМЫ.
ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ.
Существуют только в нашем воображении.
Являются элементарными (бесконечно малыми).
Не нарушают наложенных на систему связей.
Эти перемещения называются возможными (или виртуальными) перемещениями. Они удовлетворяют следующим требованиям:
Слайд 8Возможное перемещение точки отличается от действительного прежде всего тем, что
она его не совершает, а только может совершить .
Это отражается
в обозначениях: обычно элементарное действительное перемещение обозначается как ds, dх, dу, dz и т. д., возможное перемещение точки обозначается δs, δх, δу, δz и т. д.В математике символом «d» обозначается дифференциал функции, а символом «δ» обозначают вариацию функции. Однако формально они вычисляются одинаково.
При стационарных связях действительное перемещение точки
При нестационарных связях таких совпадений нет.
совпадает с одним из возможных
Слайд 9В общем случае система может иметь множество различных перемещений. Однако
для любой из систем, которые будут рассматриваться, можно указать некоторое
число таких независимых между собой перемещений, что всякое другое возможное перемещение может быть через них выражено.Опр. Возможными (или виртуальными) перемещениями механической системы называется любая совокупность элементарных перемещений точек этой системы из занимаемого в данный момент времени положения, которые допускаются всеми наложенными на систему связями.
Аналогом существования независимых величин, с помощью которых можно выразить другие величины, являются единичные орты декартовой системы координат
Слайд 10Через них можно выразить любой радиус – вектор
rх
rу
rz
Опр. Число
независимых между собой возможных перемещений механической системы называется числом степеней
свободы этой системы.Для точки, находящейся на некоторой поверхности, любое возможное перемещение
вдоль этой плоскости можно выразить через два независимых перемещения
в виде
Вывод. У механической системы с геометрическими связями число независимых координат, определяющих положение системы, совпадает с числом ее степеней свободы.
Поэтому у такой системы число степеней свободы можно определять как по числу независимых возможных перемещений, так и по числу независимых координат.
Слайд 11Возможная работа активной силы
а возможная работа реакции
обозначается символом
Опр. Возможной работой называется элементарная работа, которую действующая на материальную точку сила могла бы совершить на перемещении, совпадающем с возможным перемещением этой точки.
Принцип возможных перемещений устанавливает общие условия равновесия.
ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ.
Принцип формулируется в случае, когда все наложенные на систему связи стационарные.
связи - символом
Слайд 12Опр. Идеальными называются связи, для которых элементарная работа их реакций
на любом возможном перемещении системы равна нулю, т. е.
Это равенство
может быть представлено в аналитической формеПринцип возможных перемещений. Для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении системы была равна нулю, т.е.
(1)
(2)
Слайд 13Примечание. Скользящая заделка - это заделка, которая
«запрещает» поворот, но
не ограничивает
поступательное перемещение вдоль направляющих, по которым заделка может
скользить. Реакции скользящей заделки: реакция, перпендикулярная
направляющим, и реактивный момент – МА.
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ ОПОР С ПОМОЩЬЮ ПРИНЦИПА ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ.
На составную балку АВ действует распределенная нагрузка интенсивности q = 2 кН/м, наклонная сила F = 4 кН и пара сил с моментом М = 5 кН м. а = 2 м.
Наложены связи: в точке В – неподвижная шарнирная опора, в точке Е – горизонтальная скользящая заделка.
О п р е д е л и т ь: XВ, УВ, УЕ, МЕ.
Слайд 14Перемещения
направлены по соответствующим возможным скоростям
А) Определим горизонтальную реакцию в шарнире В
1. Заменим неподвижный шарнир В подвижным шарниром и реакцией
2. Сообщим балке АВ возможное перемещение.
Часть балки АС может поступательно перемещаться влево или вправо по горизонтали на
3. Сумма возможных работ всех сил и пар сил, действующих на балку, по принципу Лагранжа должна быть равна нулю.
ΣδАk = XВ δs + F cos (600) δs = 0,
Обозначим
Шарнир В может перемещаться влево или вправо на
М.ц.с. для ВС лежит в ∞.
∞
Т.е.
Или
Возможное перемещение балки будет поступательным на δs.
Слайд 15Поделим уравнение (1) на δs ≠ 0 и получим
XВ + F cos (600) = 0.
Откуда находим XВ
= – F cos (600) = – F / 2 = – 2 (кН).Знак минус указывает на то, что реакция направлена влево.
В) Определим вертикальную реакцию в шарнире В.
1. Заменим неподвижный шарнир В подвижным шарниром и реакцией
2. Сообщим балке АВ возможное перемещение.
Часть балки АС может перемещаться только поступательно влево или вправо, так как в точке Е скользящая заделка.
Слайд 16Следовательно,
т.е., связи, наложенные на балку, у ее части АС не допускают возможных перемещений.
Шарнир В может перемещаться только вертикально на
ΣδАk = М δφ – F cos (300) 2 а δφ + УВ 4 а δφ = 0.
Откуда находим УВ = F cos (300) / 2 – М / (4а) = 1,12 (кН).
М. ц. с. для части балки СВ будет в точке С.
Часть балки ВС может поворачиваться вокруг м. ц. с. (т. С) на угол δφ.
3. Сумма возможных работ всех сил и пар сил, действующих на балку, по принципу Лагранжа должна быть равна нулю.
Примечание. Применим выражение для работы силы, приложенной к вращающемуся телу: δА = ± М0Z(F) · δφ .
Слайд 17С) Найдем момент пары сил, возникающей в скользящей заделки, наложенной
в точке Е.
1. Заменим скользящую заделку шарнирно подвижной опорой и
неизвестным реактивным моментом МЕ.2. Сообщим балке АВ возможное перемещение.
Связи допускают только поворот части балки ВС вокруг шарнира В на угловое перемещение δφ1.
3. Составим уравнение возможных работ (1).
ΣδА k = – М δφ1 – F cos (300) 2 а δφ1 + МЕ δφ2 + Q 3а δφ2 = 0. (3)
М.ц.с. для части балки АС будет в точке Е.
Обозначим угол поворота АС вокруг м. ц. c. через δφ2 .
Выразим δφ2 через δφ1.
δsc = 4 a δφ1 = 2 a δφ2, т. е. δφ2 = 2 δφ1.
Слайд 18Двойная скользящая заделка – связь которая допускает любое поступательное перемещение
в плоскости действия сил, но исключает возможность поворота.
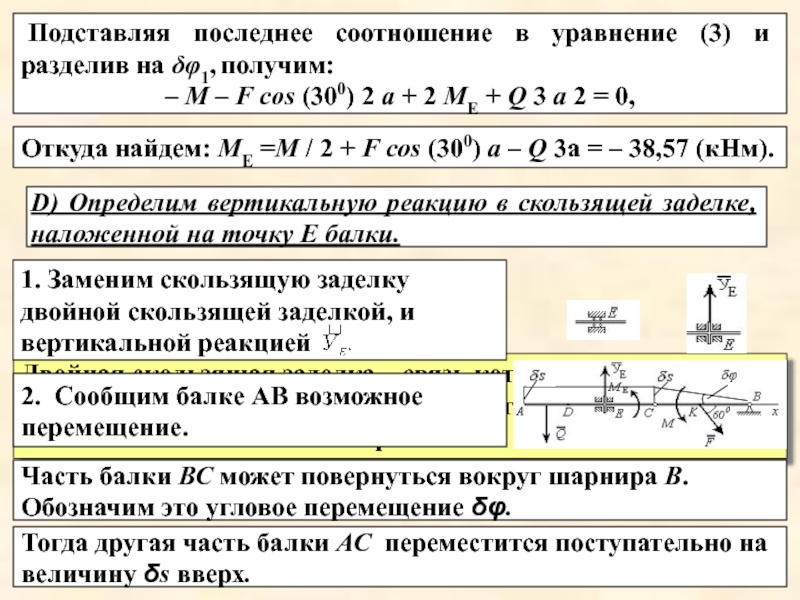
Подставляя последнее соотношение
в уравнение (3) и разделив на δφ1, получим: – М – F cos (300) 2 а + 2 МЕ + Q 3 а 2 = 0,
Откуда найдем: МЕ =М / 2 + F cos (300) а – Q 3а = – 38,57 (кНм).
D) Определим вертикальную реакцию в скользящей заделке, наложенной на точку Е балки.
1. Заменим скользящую заделку двойной скользящей заделкой, и вертикальной реакцией
2. Сообщим балке АВ возможное перемещение.
Часть балки ВС может повернуться вокруг шарнира В. Обозначим это угловое перемещение δφ.
Тогда другая часть балки АС переместится поступательно на величину δs вверх.
Слайд 193. Составим уравнение возможных работ (1).
ΣδМk = – М δφ
– F cos (300) 2а δφ – Q δs +
УЕ δs = 0. (4) Учитывая, что δφ = 4 а δs, из уравнения (4) найдем
УЕ = М /4а + F cos (300) / 2 + Q = 10,36 (кН).
Е) Сделаем проверку.
Используем уравнения равновесия в основной форме:
ΣFkX = 0, ΣFkУ = 0,
ΣFkX = ХВ + F cos600 = 0, (1)
ΣFkУ = УВ + УЕ – Q – F cos300 = 0, (2)
= Q 5а –УЕ 2а + МЕ + М – F cos (300) 2а + УВ 4а = 0. (3)
Заменим все внешние опоры их реакциями.
Слайд 20Примечание 2. В качестве моментной точки в уравнении (3) необходимо
всегда выбирать точку С, что позволит проверить все вертикальные реакции
и реактивный момент.Примечание 1. В тех вариантах, где нет жесткой заделки или скользящей заделки, уравнение (3) (ΣМС = 0) можно не составлять.
Подставляя в уравнение (1) найденную реакцию ХВ , получим:
ΣFkX = XВ + F cos (600) = – 2 + 4/2 ≡ 0.
Подставляя в уравнение (2) реакции УВ и УЕ , найдем:
ΣFkУ = УВ + УЕ – Q – F cos300 = 1,12 + 10,36 – 8 – 3,48 ≡ 0.
= 8 .5 . 2 – 10,36 . 2 . 2 – 38,57 + 5 – 4 . 2 . 2 / 2 +1,12 . 4 .2=
= 93,96 – 93,88 = 0,08 ≈ 0.
Ответ: УВ = 1,12кН, XВ = – 2кН, УЕ =10,36кН, МЕ = – 38,57кНм.
Подставляя в уравнение (3) реакции УВ ,УЕ и момент МЕ, найдем:
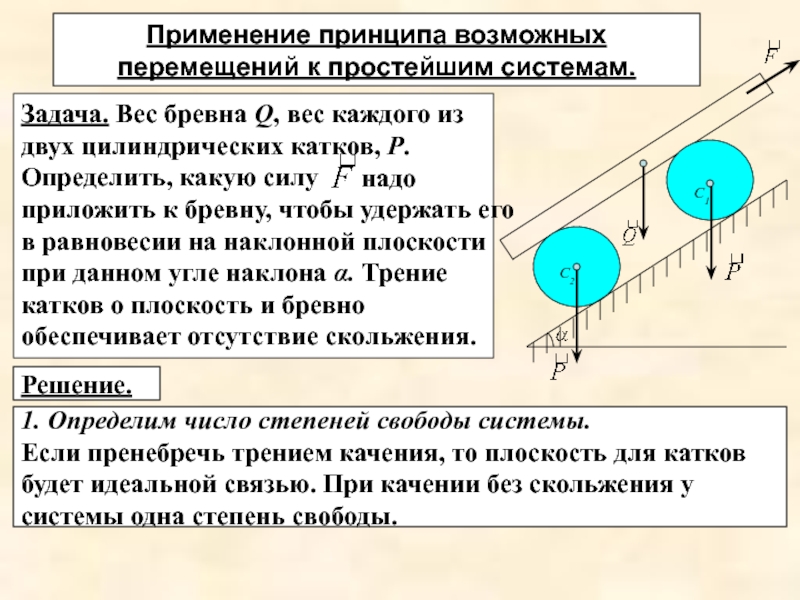
Слайд 21Задача. Вес бревна Q, вес каждого из двух цилиндрических катков,
Р.
Определить, какую силу
надо приложить к бревну, чтобы удержать его в равновесии на наклонной плоскости при данном угле наклона α. Трение катков о плоскость и бревно обеспечивает отсутствие скольжения. Применение принципа возможных перемещений к простейшим системам.
Решение.
1. Определим число степеней свободы системы.
Если пренебречь трением качения, то плоскость для катков будет идеальной связью. При качении без скольжения у системы одна степень свободы.
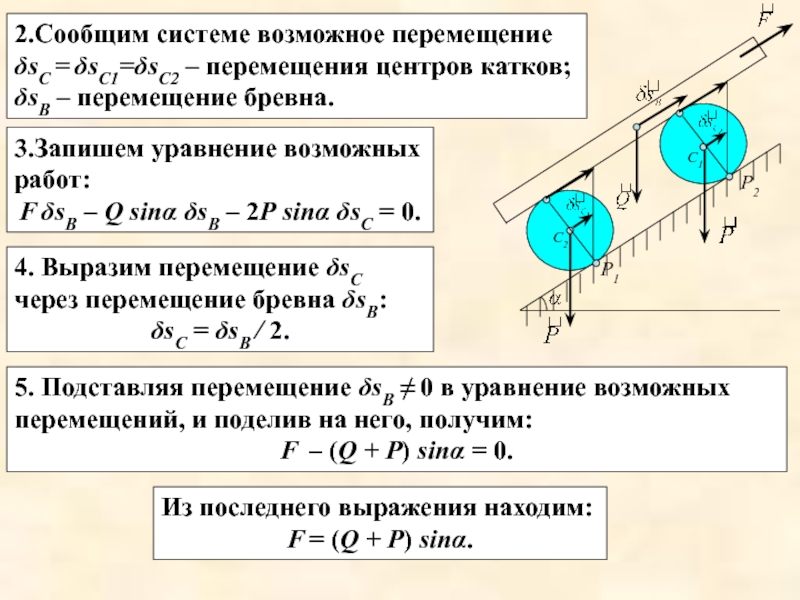
Слайд 222.Сообщим системе возможное перемещение
δsС = δsС1=δsС2 – перемещения центров катков;
δsВ
– перемещение бревна.
3.Запишем уравнение возможных работ:
F δsB – Q sinα
δsB – 2Р sinα δsC = 0. 4. Выразим перемещение δsC через перемещение бревна δsB:
δsC = δsB / 2.
5. Подставляя перемещение δsВ ≠ 0 в уравнение возможных перемещений, и поделив на него, получим:
F – (Q + Р) sinα = 0.
Из последнего выражения находим:
F = (Q + Р) sinα.
Слайд 23Если ко всем точкам системы кроме действующих активных сил
прибавить соответствующие силы инерции
Рассмотрим систему материальных точек, на которую наложены идеальные связи.
то согласно принципу Даламбера полученная система сил будет находиться в равновесии.
ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
Применяя последовательно принцип Даламбера и принцип возможных перемещений получим общий метод решения задач динамики.
и реакций связей
Применяя к этим силам принцип Лагранжа, получим
Слайд 24Так как на систему наложены идеальные связи, то
Тогда
(3)
Равенство
(3) выражает принцип Даламбера – Лагранжа.
Принцип Даламбера – Лагранжа. При
движении механической системы с идеальными связями в каждый момент времени сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы равна нулю.Равенство (3) называют также общим уравнением динамики.
В аналитической форме уравнение (3) имеет вид
(4)
Уравнения (3) и (4) позволяют составить дифференциальные уравнения движения системы.
Слайд 25Пример применения принцип Даламбера – Лагранжа.
В подъемнике к шестерне 1,
имеющей вес Р1 и радиус инерции ρ1, приложен вращающий момент
М. Определить ускорение поднимаемого груза 3 весом Q, пренебрегая весом веревки и трением в осях.Барабан, на котором на котором намотана веревка, жестко скреплен с другой шестерней; их общий вес равен Р2 , а радиус инерции относительно оси вращения ρ2.. Радиусы шестерней равны соответственно r1, r2, а радиус барабана r.
Изображаем действующую на систему активную силу
и вращающий момент М (другие силы работу не совершают).
Решение.
Слайд 262. Присоединим к ним силу инерции груза
и пары
с моментами
, к которым приводятся силы инерции вращающихся тел. Эти величины по модулю равны:Сообщая системе возможное перемещение и составляя уравнение (3), получим
3. Выражая все перемещения через δφ2
или
Слайд 27Окончательно уравнение движения примет вид
4. Входящие сюда величины
выразим через
искомое
В результате найдем окончательно
Слайд 28Задание 25
Варианты ответа
1) 15 м/с2
2) 20 м/с2
3) 5 м/с2
4) 10 м/с2
Общее уравнение динамики
Р2δs – F2И δs
– F1И δs – Р1δs = 0.Поделив уравнение на δs, и вычисляя силы инерции
F2И = m2 a, F1И = m1 a, получим g (3 m1 - m1) = a (3 m1 + m1).
Откуда а = g/2 = 5 м/с2.
Грузы 1 и 2, массы которых m2 = 3m1, прикреплены к тросу, переброшенному через блок радиуса r.
Если принять g =10 м/с2 и пренебречь массой блока, то ускорение грузов равно…
Слайд 29Задание 26
Варианты ответа
1) 17 Нм
2) 11 Нм
3) 29 Нм
4) 27 Нм
Общее уравнение динамики: Мδφ – МИ δφ
– F1И δs – Р1δs = 0.Тело 1 поднимается с ускорением а = 3 м/с2, массы тел m1 = m2 = 20 кг, радиус барабана 2, который можно считать однородным цилиндром, r = 0,1м (g = 10 м/с2).
Тогда модуль момента М пары сил равен…
Вычислим силы инерции
F1И = m1a, МИ = J ε = (m2 r2 /2) ·a/ r = m2 a r /2.
Выразим угловое перемещение через линейное δφ = δs / r.
М ⋅ δs / r – m2⋅ a ⋅ r (δs / r) /2 – m1⋅ a ⋅ δs – m1⋅ g ⋅ δs = 0.
Поделив уравнение на δs, найдем: М/ r– m1g – а(m1+ m2/2) = 0.
Откуда: М = (m1g + а(m1+ m2/2)) r = 29 Нм.