TheSlide.ru

Признаки равенства треугольников

Содержание

1. Признаки равенства треугольников
2. ТреугольникВАСДано:∆АВСА, В, С – вершины ∆АВСАВ, ВС,
3. Два треугольника называются равными, если их можно совместить наложением.Равенство треугольниковВАСА1В1С1∆АВС = ∆А1В1С1
4. Если два треугольника равны, то элементы (т.е.
5. ТеоремаЕсли две стороны и угол между ними
6. Перпендикуляр к прямойДано:прямая а, АН – перпендикуляр к аАН  аН – основание перпендикуляраАаН
7. ТеоремаИз точки не лежащей на прямой, можно
8. Определение Отрезок, соединяющий вершину треугольника с серединой
9. ВАСЛюбой треугольник имеет три медианы.Медианы треугольника пересекаются
10. Определение Отрезок биссектрисы угла треугольника, соединяющий вершину
11. ВАСЛюбой треугольник имеет три биссектрисы.Биссектрисы треугольника пересекаются
12. Определение Перпендикуляр, проведённый из вершины треугольника к
13. ВАСЛюбой треугольник имеет три высоты.Высоты треугольника или
14. Дано: ∆АВСАВ = АС АВ, АС –
15. Дано: ∆АВСАВ = АС = ВСВАСРавносторонний треугольникОпределение Треугольник, все стороны которого равны называется равносторонним.
16. Дано: ∆АВСАВ = АС ВАССвойства равнобедренного треугольникаТеорема
17. Дано: ∆АВСАВ = АС; 1 = 2.ВАССвойства
18. Утверждение 1Высота равнобедренного треугольника, проведённая к основанию,
19. ТеоремаЕсли сторона и два прилежащих к ней
20. ТеоремаЕсли три стороны одного треугольника соответственно равны
21. Геометрия, 7 – 9: Учеб. для общеобразоват.
22. Скачать презентанцию

ТреугольникВАСДано:∆АВСА, В, С – вершины ∆АВСАВ, ВС, АС– стороны ∆АВСА, В, С – углы ∆АВСВершины (3)Стороны (3)Углы (3)

Главная
Разное
Признаки равенства треугольников

Слайды и текст этой презентации

Слайд 1Признаки равенства треугольников Геометрия 7 класс
МБОУ СОШ №5 – «Школа здоровья

и развития»
Учитель математики: Семёнова Елена Юрьевна

Признаки равенства треугольников Геометрия 7 классМБОУ СОШ №5 – «Школа здоровья и развития»Учитель математики: Семёнова Елена

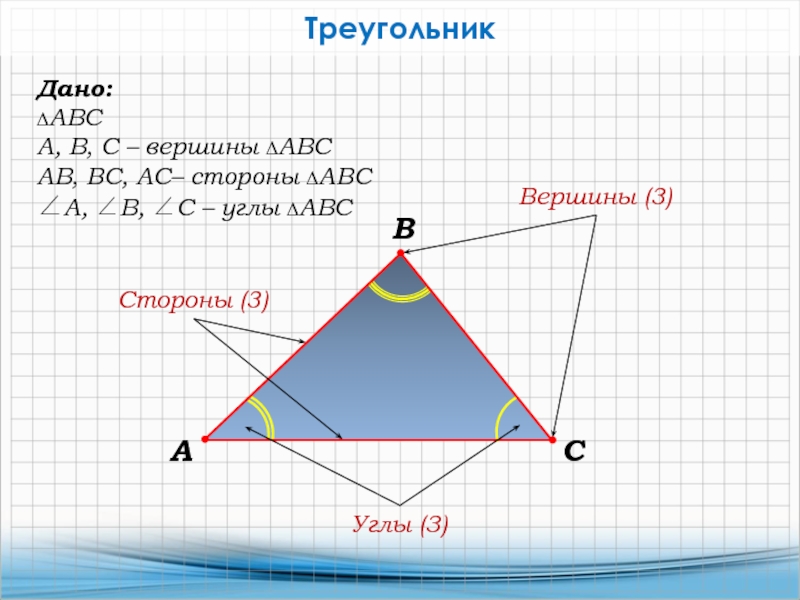
Слайд 2Треугольник
В
А
С
Дано:
∆АВС
А, В, С – вершины ∆АВС
АВ, ВС, АС– стороны ∆АВС
А,

В, С – углы ∆АВС
Вершины (3)
Стороны (3)
Углы (3)

ТреугольникВАСДано:∆АВСА, В, С – вершины ∆АВСАВ, ВС, АС– стороны ∆АВСА, В, С – углы ∆АВСВершины (3)Стороны (3)Углы

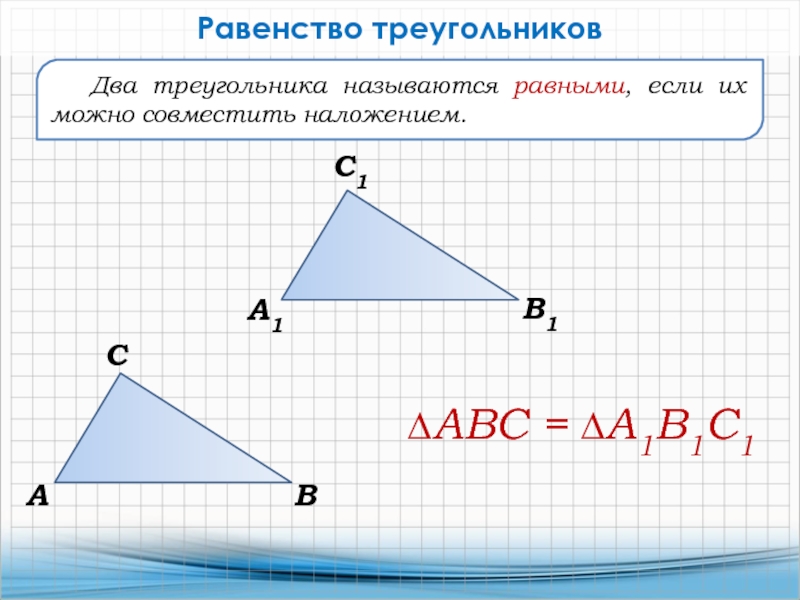
Слайд 3Два треугольника называются равными, если их можно совместить наложением.
Равенство треугольников
В
А
С
А1
В1
С1
∆АВС

= ∆А1В1С1

Два треугольника называются равными, если их можно совместить наложением.Равенство треугольниковВАСА1В1С1∆АВС = ∆А1В1С1

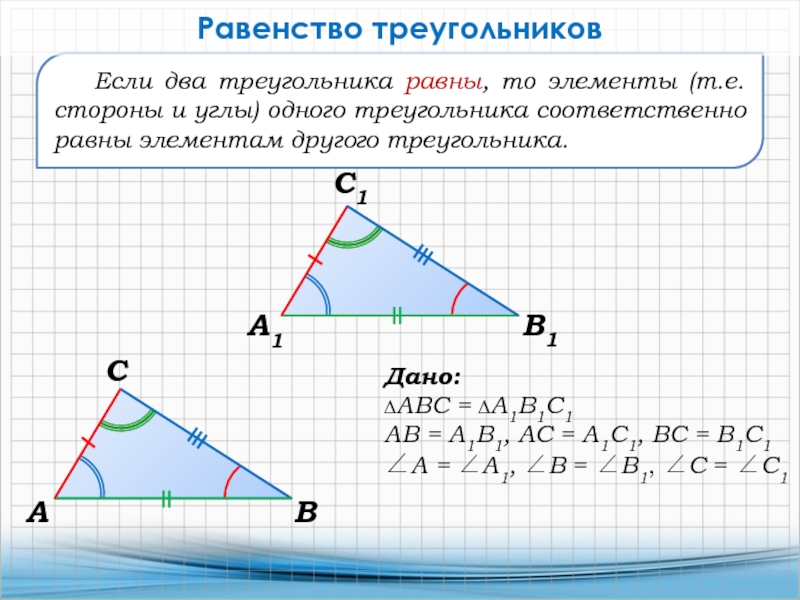
Слайд 4Если два треугольника равны, то элементы (т.е. стороны и углы)

одного треугольника соответственно равны элементам другого треугольника.
Равенство треугольников
В
А
С
А1
В1
С1
Дано:
∆АВС = ∆А1В1С1
АВ

= А1В1, АС = А1С1, ВС = В1С1
А = А1, В = В1, С = С1

Если два треугольника равны, то элементы (т.е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.Равенство

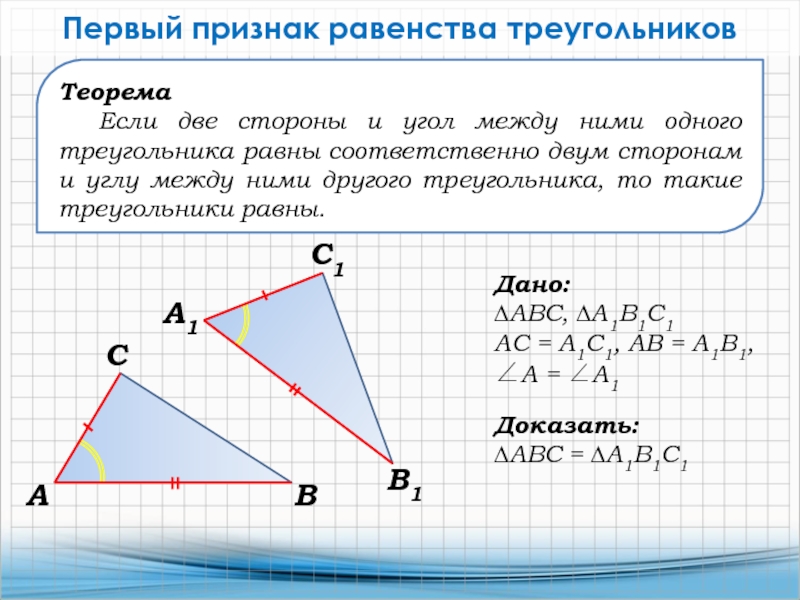
Слайд 5Теорема
Если две стороны и угол между ними одного треугольника равны

соответственно двум сторонам и углу между ними другого треугольника, то

такие треугольники равны.

Первый признак равенства треугольников

Дано:
∆АВС, ∆А1В1С1
АС = А1С1, АВ = А1В1,
А = А1

Доказать:
∆АВС = ∆А1В1С1

ТеоремаЕсли две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними

Слайд 6Перпендикуляр к прямой
Дано:
прямая а,
АН – перпендикуляр к а
АН 

а
Н – основание перпендикуляра
А
а
Н

Перпендикуляр к прямойДано:прямая а, АН – перпендикуляр к аАН  аН – основание перпендикуляраАаН

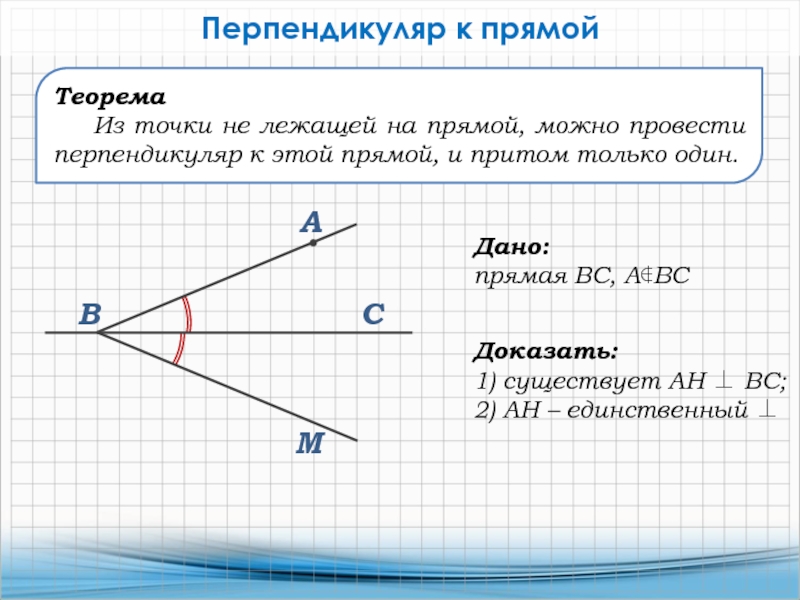
Слайд 7Теорема
Из точки не лежащей на прямой, можно провести перпендикуляр к

этой прямой, и притом только один.
Перпендикуляр к прямой
В
Дано:
прямая ВС, АВС
Доказать:
1)

существует АН  ВС;
2) АН – единственный 

А

М

С

ТеоремаИз точки не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.Перпендикуляр к

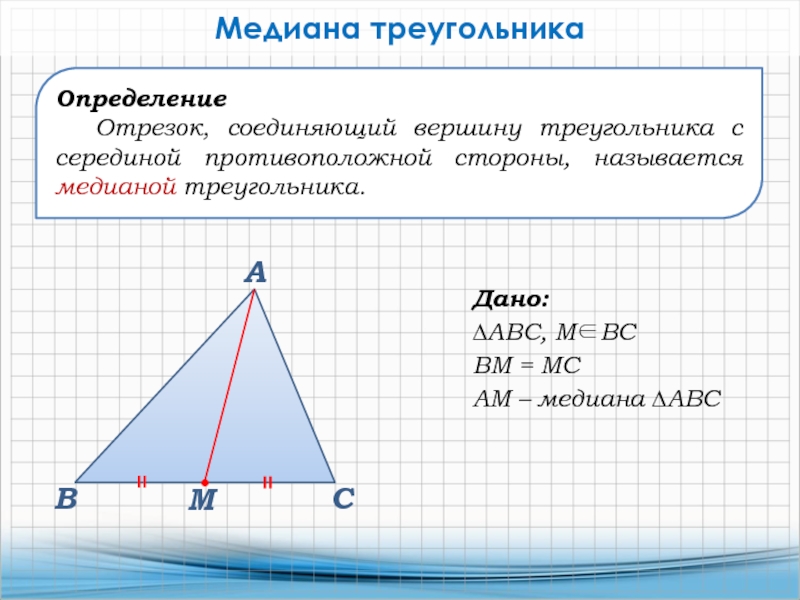
Слайд 8Определение
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется

медианой треугольника.
Медиана треугольника
Дано:
∆АВС, МВС
ВМ = МС
АМ – медиана ∆АВС
М

Определение Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.Медиана треугольникаДано:∆АВС, МВСВМ = МСАМ –

Слайд 9В
А
С
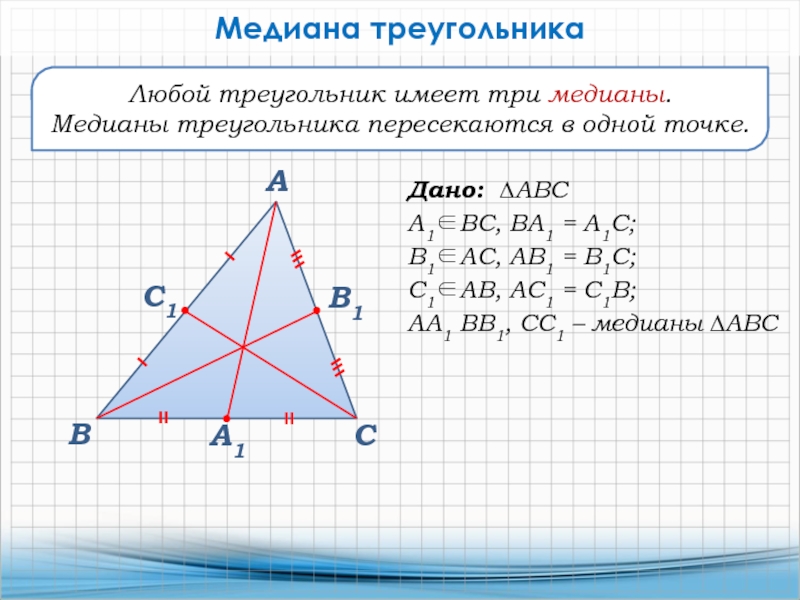
Любой треугольник имеет три медианы.
Медианы треугольника пересекаются в одной точке.
Медиана

треугольника
Дано: ∆АВС
А1ВС, ВА1 = А1С;
В1АС, АВ1 = В1С;
С1АВ, АС1 =

С1В;
АА1 ВВ1, СС1 – медианы ∆АВС

А1

С1

В1

ВАСЛюбой треугольник имеет три медианы.Медианы треугольника пересекаются в одной точке.Медиана треугольникаДано: ∆АВСА1ВС, ВА1 = А1С;В1АС, АВ1 =

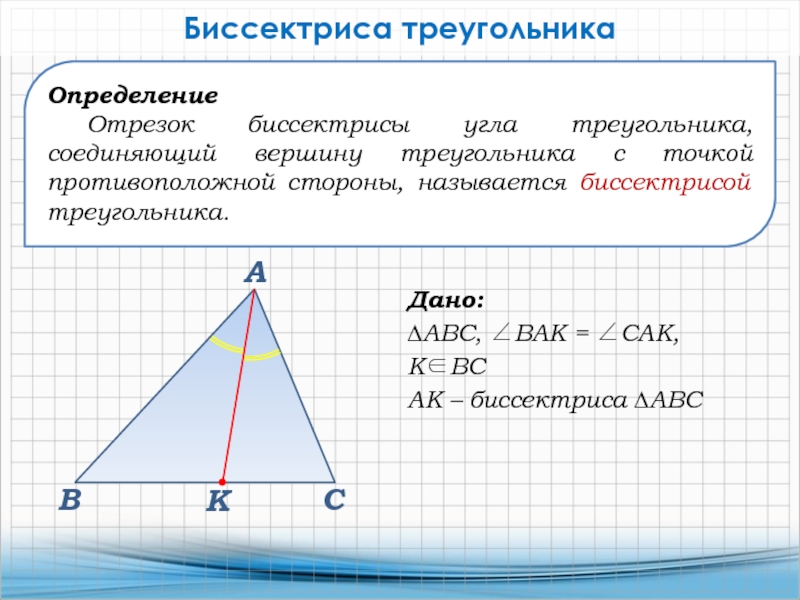
Слайд 10Определение
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой

противоположной стороны, называется биссектрисой треугольника.
Биссектриса треугольника
Дано:
∆АВС, ВАК = САК,
КВС
АК –

биссектриса ∆АВС

К

Определение Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.Биссектриса треугольникаДано:∆АВС, ВАК

Слайд 11В
А
С
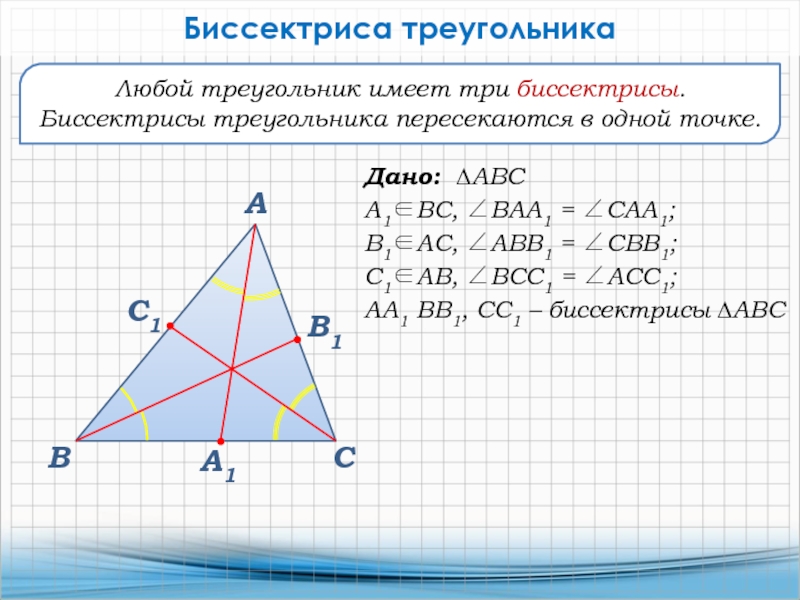
Любой треугольник имеет три биссектрисы.
Биссектрисы треугольника пересекаются в одной точке.
Дано:

∆АВС
А1ВС, ВАА1 = САА1;
В1АС, АВВ1 = СВВ1;
С1АВ, ВСС1 = АСС1;
АА1

ВВ1, СС1 – биссектрисы ∆АВС

А1

С1

В1

Биссектриса треугольника

ВАСЛюбой треугольник имеет три биссектрисы.Биссектрисы треугольника пересекаются в одной точке.Дано: ∆АВСА1ВС, ВАА1 = САА1;В1АС, АВВ1 = СВВ1;С1АВ,

Слайд 12Определение
Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную

сторону, называется высотой треугольника.
Высота треугольника
Дано:
∆АВС, АН  ВС, НВС
АН –

высота ∆АВС

Н

Определение Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.Высота треугольникаДано:∆АВС, АН 

Слайд 13В
А
С
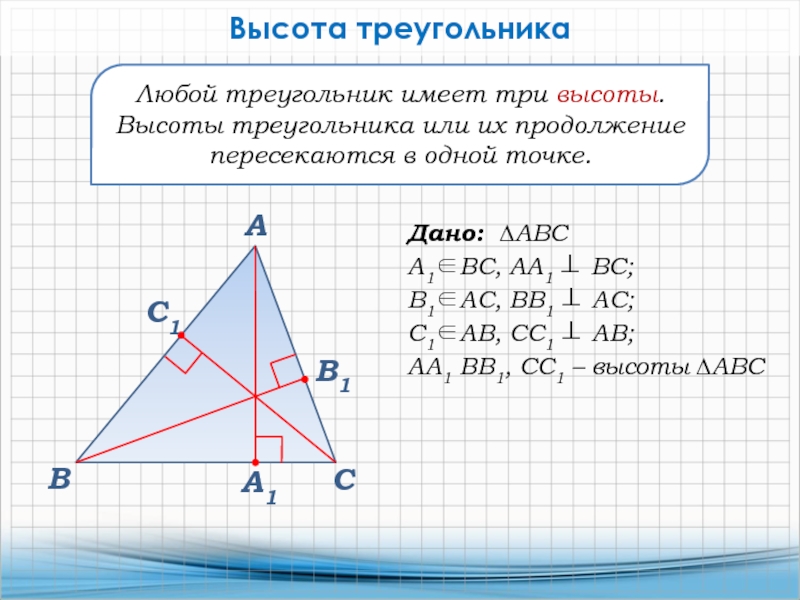
Любой треугольник имеет три высоты.
Высоты треугольника или их продолжение пересекаются

в одной точке.
Дано: ∆АВС
А1ВС, АА1  ВС;
В1АС, ВВ1  АС;
С1АВ,

СС1  АВ;
АА1 ВВ1, СС1 – высоты ∆АВС

А1

С1

В1

Высота треугольника

ВАСЛюбой треугольник имеет три высоты.Высоты треугольника или их продолжение пересекаются в одной точке.Дано: ∆АВСА1ВС, АА1  ВС;В1АС,

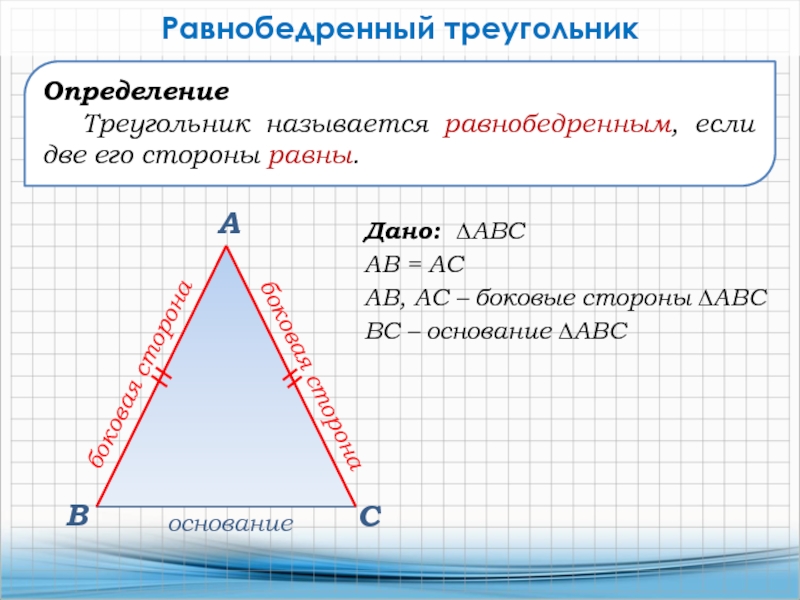
Слайд 14Дано: ∆АВС
АВ = АС
АВ, АС – боковые стороны ∆АВС

ВС – основание ∆АВС
В
А
С
Равнобедренный треугольник
Определение
Треугольник называется равнобедренным, если

две его стороны равны.

боковая сторона

основание

боковая сторона

Дано: ∆АВСАВ = АС АВ, АС – боковые стороны ∆АВС ВС – основание ∆АВС ВАСРавнобедренный треугольникОпределение Треугольник

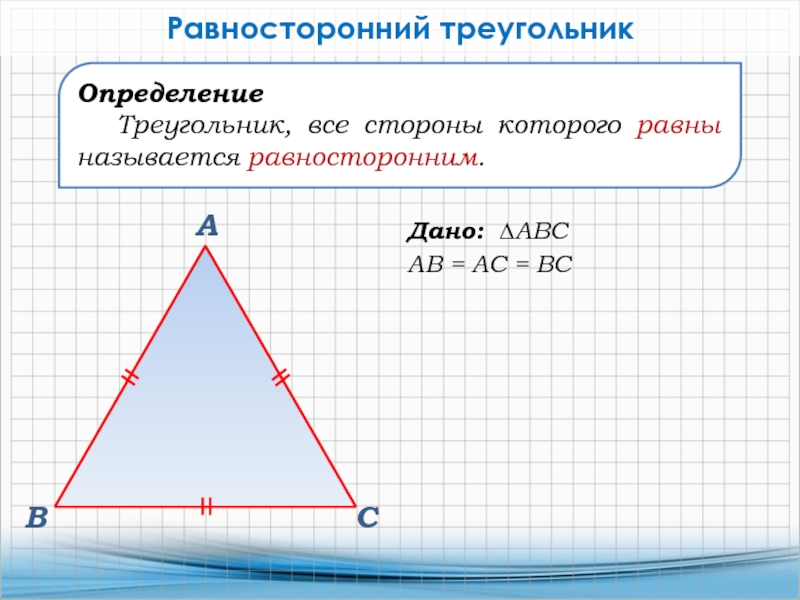
Слайд 15Дано: ∆АВС
АВ = АС = ВС
В
А
С
Равносторонний треугольник
Определение
Треугольник, все стороны

которого равны называется равносторонним.

Дано: ∆АВСАВ = АС = ВСВАСРавносторонний треугольникОпределение Треугольник, все стороны которого равны называется равносторонним.

Слайд 16Дано: ∆АВС
АВ = АС
В
А
С
Свойства равнобедренного треугольника
Теорема 1
В равнобедренном

треугольнике углы при основании равны.
1
2
Доказать:
В = С
D

Дано: ∆АВСАВ = АС ВАССвойства равнобедренного треугольникаТеорема 1 В равнобедренном треугольнике углы при основании равны.12Доказать:В = СD

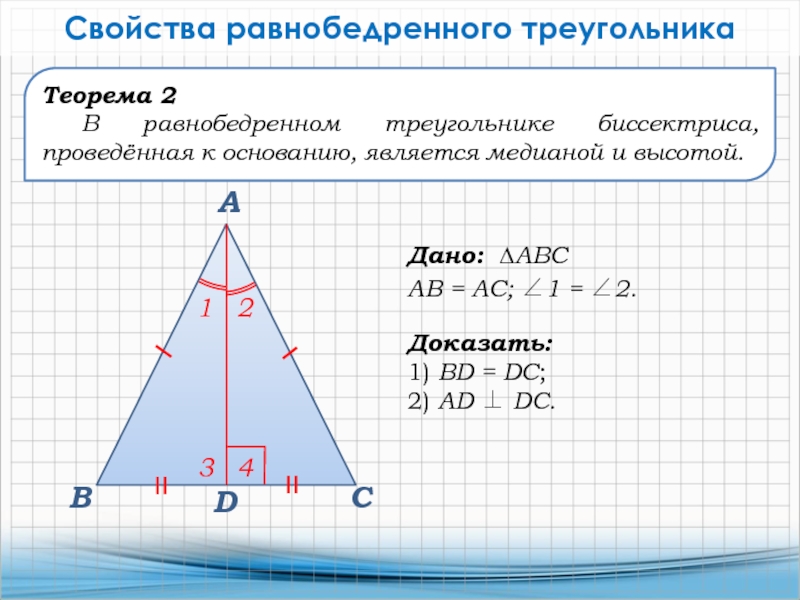
Слайд 17Дано: ∆АВС
АВ = АС; 1 = 2.
В
А
С
Свойства равнобедренного треугольника
Теорема 2

В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и

высотой.

1

2

3

4

Доказать:
1) BD = DC;
2) AD  DC.

D

Дано: ∆АВСАВ = АС; 1 = 2.ВАССвойства равнобедренного треугольникаТеорема 2 В равнобедренном треугольнике биссектриса, проведённая к основанию,

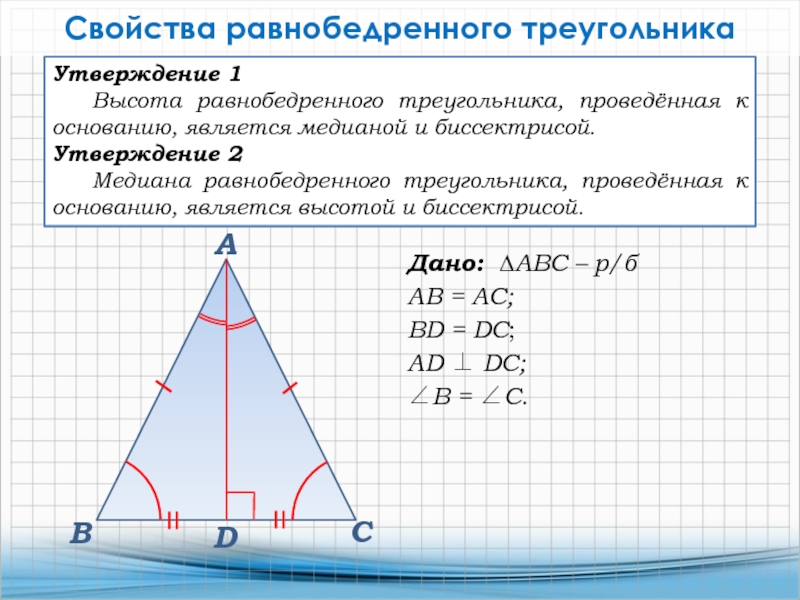
Слайд 18Утверждение 1
Высота равнобедренного треугольника, проведённая к основанию, является медианой и

биссектрисой.
Утверждение 2
Медиана равнобедренного треугольника, проведённая к основанию, является высотой и

биссектрисой.

Дано: ∆АВС – р/б
АВ = АС;
BD = DC;
AD  DC;
В = С.

Свойства равнобедренного треугольника

Утверждение 1Высота равнобедренного треугольника, проведённая к основанию, является медианой и биссектрисой.Утверждение 2Медиана равнобедренного треугольника, проведённая к основанию,

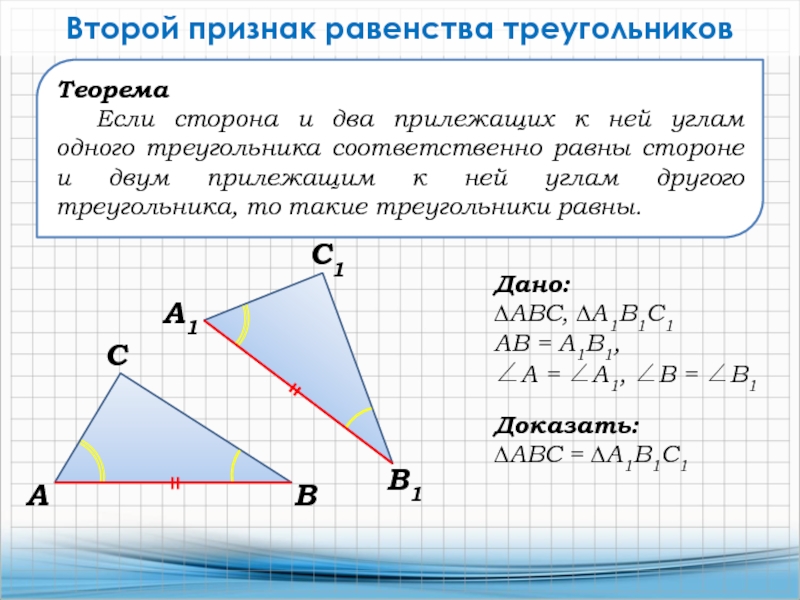
Слайд 19Теорема
Если сторона и два прилежащих к ней углам одного треугольника

соответственно равны стороне и двум прилежащим к ней углам другого

треугольника, то такие треугольники равны.

Второй признак равенства треугольников

Дано:
∆АВС, ∆А1В1С1
АВ = А1В1,
А = А1, В = В1

Доказать:
∆АВС = ∆А1В1С1

ТеоремаЕсли сторона и два прилежащих к ней углам одного треугольника соответственно равны стороне и двум прилежащим к

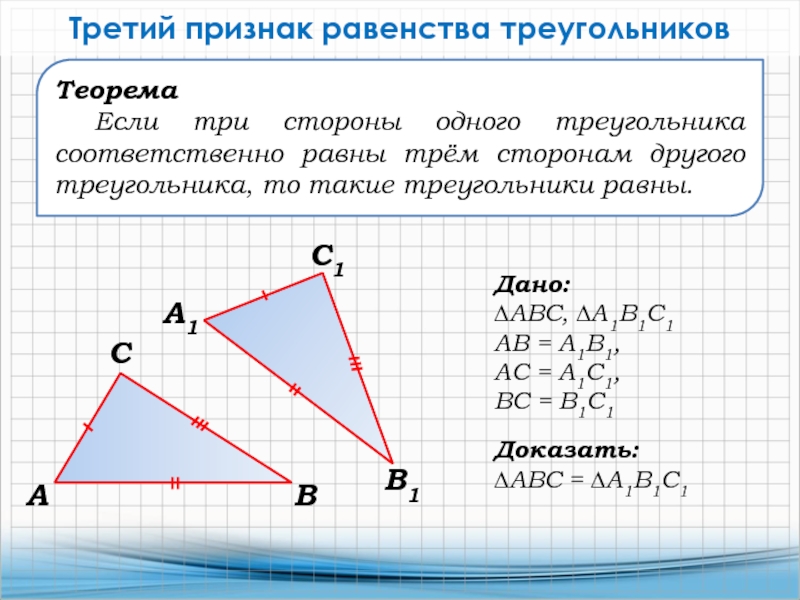
Слайд 20Теорема
Если три стороны одного треугольника соответственно равны трём сторонам другого

треугольника, то такие треугольники равны.
Третий признак равенства треугольников
Дано:
∆АВС, ∆А1В1С1
АВ =

А1В1,
АС = А1С1,
ВС = В1С1

Доказать:
∆АВС = ∆А1В1С1

ТеоремаЕсли три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.Третий признак равенства

Слайд 21Геометрия, 7 – 9: Учеб. для общеобразоват. учреждений / Л.С.

Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение,

2012.
http://www.graphicsfuel.com/2012/07/pencil-icon-vector-psd/ - карандаш

Использованы ресурсы

Геометрия, 7 – 9: Учеб. для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.

Скачать презентацию

Теги

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей