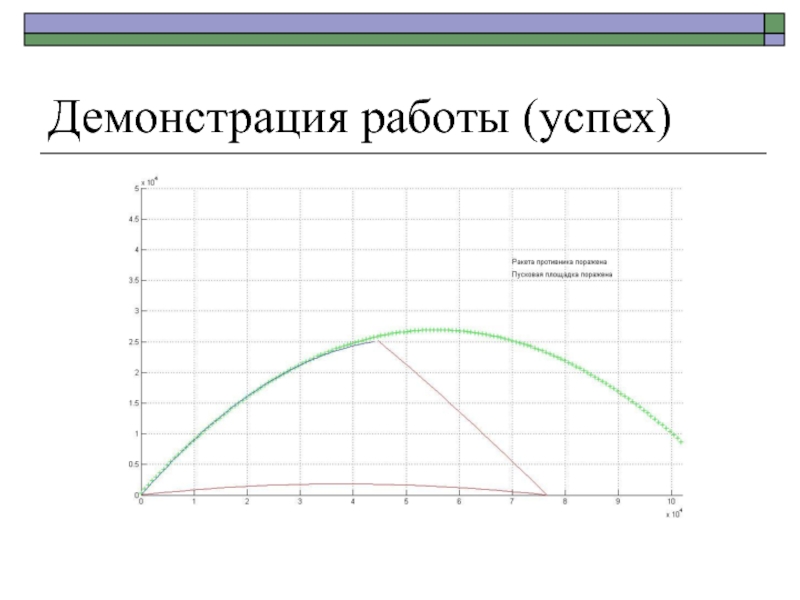
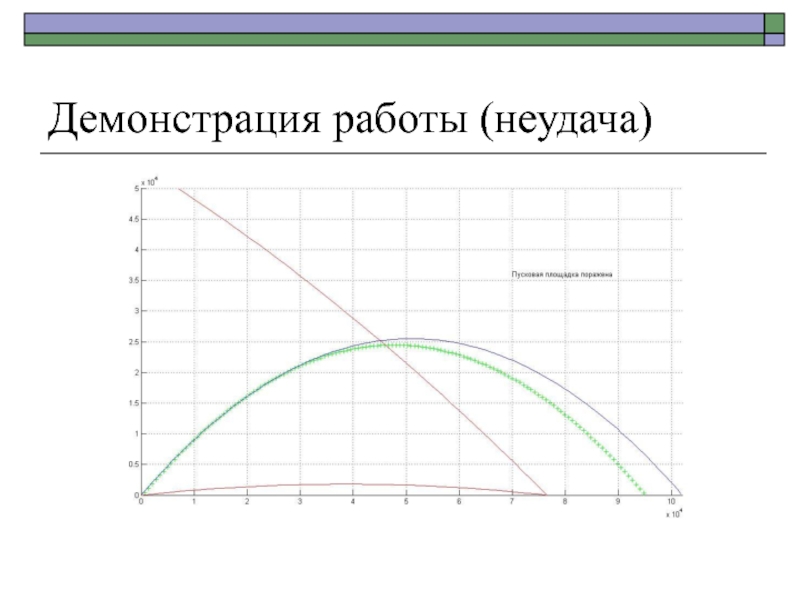
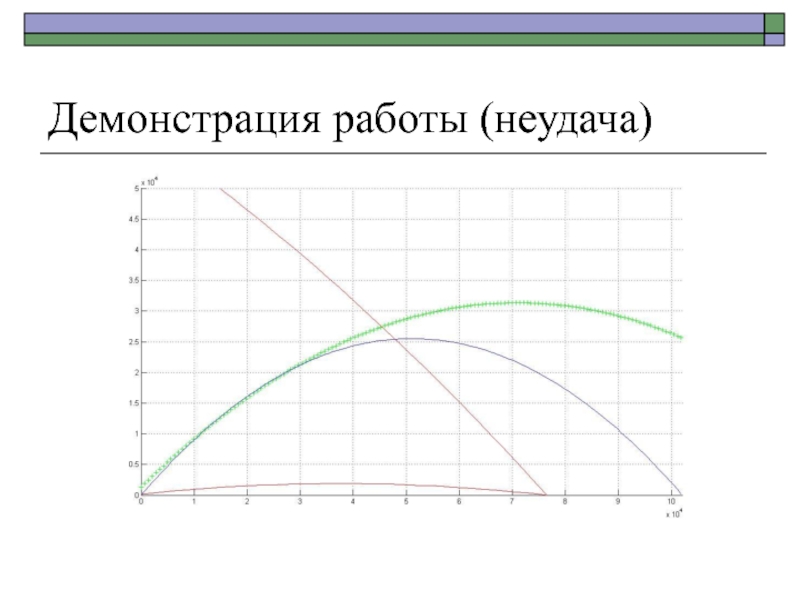
Имеются две антиракеты: одна должна сбить ракету в полёте, другая
– накрыть пусковую площадку.Необходимо определить время и угол старта антиракет.



![ПРО-2011 Анализ задачиПараметр t – целое число из промежутка [40;T1]Если t и Анализ задачиПараметр t – целое число из промежутка [40;T1]Если t и β перебирать, программа будет работать долго.](/img/thumbs/3372d5a7144f44b4b644effe4cd05832-800x.jpg)