Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ПРОЕКТ ИНДИВИДУАЛЬНЫЙ На тему: Применение математики в поисках оптимального
Содержание
- 1. ПРОЕКТ ИНДИВИДУАЛЬНЫЙ На тему: Применение математики в поисках оптимального
- 2. Содержание: ВВЕДЕНИЕМЕТОДЫ НАХОЖДЕНИЯ ОПТИМАЛЬНЫХ РЕШЕНИЙ Дифференциальное исчисление Метод
- 3. Введение В современном
- 4. Слайд 4
- 5. Цели и актуальность проекта:
- 6. Задачи проекта: 1.Собрать материал по данной теме2.
- 7. 1. МЕТОДЫ НАХОЖДЕНИЯ ОПТИМАЛЬНЫХ РЕШЕНИЙ
- 8. 1. МЕТОДЫ НАХОЖДЕНИЯ ОПТИМАЛЬНЫХ РЕШЕНИЙ
- 9. 2. Дифференциальное исчисление
- 10. Однако, несмотря на простоту,
- 11. В экономике
- 12. 3. МЕТОД МНОЖИТЕЛЕЙ ЛАГРАНЖА
- 13. 4. Вариационное исчисление
- 14. 5. Нелинейное программирование
- 15. Слайд 15
- 16. 6. Стохастическое программирование
- 17. Слайд 17
- 18. 7. Принцип максимума
- 19. 8. Экстремальное управление
- 20. 9. Графический метод
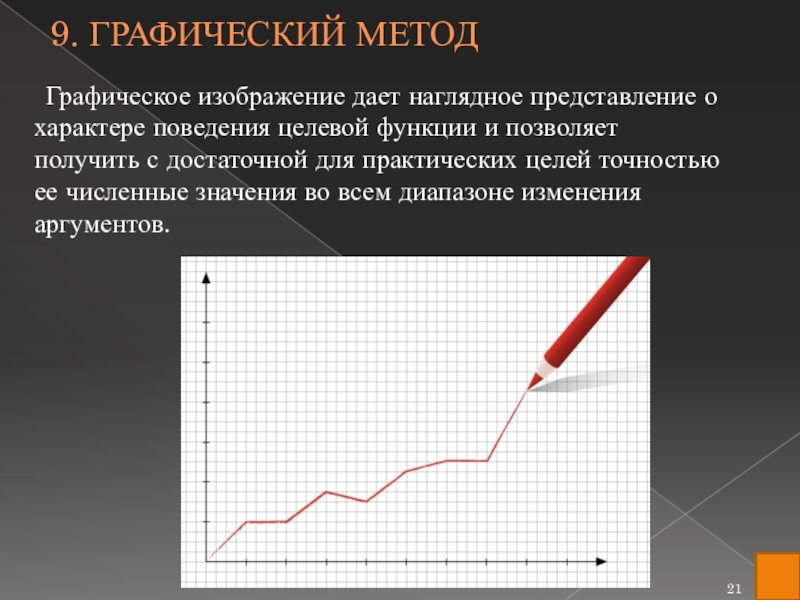
- 21. Графическое изображение дает наглядное
- 22. Заключение Тема моего
- 23. Сегодня для выработки
- 24. Список использованной литературы Замков О.О., Толстопятенков А.В.,
- 25. Слайд 25
- 26. Скачать презентанцию
Содержание: ВВЕДЕНИЕМЕТОДЫ НАХОЖДЕНИЯ ОПТИМАЛЬНЫХ РЕШЕНИЙ Дифференциальное исчисление Метод множителей Лагранжа Вариационное исчислениеНелинейное программированиеСтохастическое программированиеПринцип максимумаЭкстремальное управлениеГрафический методЗАКЛЮЧЕНИЕ Список используемой литературы
Слайды и текст этой презентации
Слайд 1ПРОЕКТ ИНДИВИДУАЛЬНЫЙ На тему: «Применение математики в поисках оптимального решения» Специальность: 07.02.01
Архитектура
Слайд 2Содержание:
ВВЕДЕНИЕ
МЕТОДЫ НАХОЖДЕНИЯ ОПТИМАЛЬНЫХ РЕШЕНИЙ
Дифференциальное исчисление
Метод множителей Лагранжа
Вариационное
исчисление
Нелинейное программирование
Стохастическое программирование
Принцип максимума
Экстремальное управление
Графический метод
ЗАКЛЮЧЕНИЕ
Список используемой литературы
Слайд 3Введение
В современном мире наблюдается широкий спрос
на технологии, позволяющие решить проблему принятия решений, их интерес заключается
в том, чтобы «достичь максимального эффекта при наименьших затратах». Все это предоставило дополнительный импульс изучению и формированию представлений о процессах принятия решений и широкого круга задач по оптимизации.Слайд 4
В настоящее время
под принятием решений понимается особый процесс человеческой деятельности, направленный на
выбор наилучшего варианта (альтернативы) действий. Процессы принятия решения лежат в основе любой целенаправленной деятельности человека. Например, при создании новой техники (машин, приборов, устройств), в строительстве при проектировании новых зданий, при организации функционирования и развития социальных процессов. В связи с этим появляется потребность в руководстве по принятию решений, которые упрощали бы этот процесс и придавали решениям большую надежность.Слайд 5Цели и актуальность проекта:
Тема проекта: «Применение
математики в поисках оптимального решения»
Актуальность исследовательской
работы: В наше время для облегчения сложных экономических ситуаций и процессов управления предприятием руководителям требуется некоторая основа и «доказанная гарантия» принимаемого решения. Неизбежно требуется формализация процесса принятия решений. Как правило, важные решения принимаются опытными людьми, довольно далекими от математики, и особенно от ее новых методов, и опасающимися больше потерять от формализации, чем выиграть.Цель: Рассказать о важности правильного анализа, который впоследствии поможет принять рациональное решение в какой-либо отрасли деятельности.
Слайд 6Задачи проекта:
1.Собрать материал по данной теме
2. Проанализировать пути, методы и
способы принятия рациональных решений
3. Разработать общий план по правильному
принятию решенийСлайд 71. МЕТОДЫ НАХОЖДЕНИЯ ОПТИМАЛЬНЫХ РЕШЕНИЙ
Промежуточным
этапом решения оптимизационной задачи является составление целевой функции. Следующим этапом,
решение которого приводит к достижению цели, является нахождение оптимума этой функции. Существующие методы поиска оптимума целевой функции разделяют на аналитические и численные. К аналитическим методам относятся дифференциальное исчисление, метод множителей Лагранжа, вариационное исчисление, а также в ряде случаев методы, основанные на принципе максимума Л. С. Понтрягина.Слайд 81. МЕТОДЫ НАХОЖДЕНИЯ ОПТИМАЛЬНЫХ РЕШЕНИЙ
К численным
методам относятся методы программирования: линейного, нелинейного, динамического, стохастического. Кроме того,
существуют методы поиска оптимального решения непосредственно на объекте - это экстремальное управление и систематическая оптимизация. Применение того или иного метода поиска окончательного решения обуславливается многими факторами, например: требуемой точностью результата, сложностью целевой функции, количеством переменных аргументов и ограничений, необходимостью знать смежные с оптимальным значения, наличием ЭВМ, квалификацией обслуживающего ее персонала, а так же наличием математического обеспечения и т.д.Мы рассмотрим наиболее распространение методы нахождения оптимальных решений.
Слайд 92. Дифференциальное исчисление
Дифференциальное исчисление является составной частью
математического анализа. Этот общеизвестный метод основан на нахождении частных производных
целевой функции по каждому переменному аргументу.Приравняв эти частные производные к нулю, решают полученную систему обычно нелинейных уравнений известными аналитическими или численными методами. Полученные значения аргументов будут соответствовать оптимальным значениям целевой функции.
Слайд 10 Однако, несмотря на простоту, этот метод применяется
весьма в ограниченных сферах деятельности. Это происходит из-за следующих условий:
целевая функция должна быть непрерывной и дифференцируемой, число переменных аргументов невелико, ограничения не учитываются. Дифференциальное исчисление - широко применяемый для экономического анализа математический аппарат. Базовой задачей экономического анализа является изучение связей экономических величин, записываемых в виде функций.2. Дифференциальное исчисление
Слайд 11 В экономике очень часто требуется
найти наилучшее (оптимальное) значение показателя: наивысшую производительность труда, максимальную прибыль,
минимальные издержки. Каждый показатель представляет собой функцию одного (нескольких) аргументов.Аппарат дифференциального исчисления применяется так же в моделях экономической динамики. Динамические модели применяются для решения таких задач, как определения оптимальной или равноместной траектории развития экономической системы, ее состояний в заданные моменты времени, анализ системы на устойчивость, анализ структурных сдвигов и т.д.
Слайд 123. МЕТОД МНОЖИТЕЛЕЙ ЛАГРАНЖА
Метод множителей
Лагранжа применяют для задач, целевая функция которых в основном соответствует приведенным
выше условиям, но при наличии ограничений типа равенств. При этом оптимальное значение целевой функции является условным, так как лежит на ограничении.Слайд 134. Вариационное исчисление
Вариационное исчисление эффективно при решении
оптимизационных задач, целевая функция которых непрерывная и дифференцируемая. Допускаются ограничения
типа равенств и неравенств. Для задач вариационного исчисления можно использовать принцип максимума Л.С. Понтрягина.Методы линейного и динамического программирований рассмотрены в отдельном разделе. Остановимся лишь на области применения нелинейного и стохастического программирования.
Слайд 145. Нелинейное программирование
Нелинейное программирование применяют для решения
задач, у которых целевая функция или ограничения не линейны. Эффективные
методы разработаны лишь для отдельных классов задач, про которые априори известно, что они не являются экстремальными. К таким задачам относятся, например, задачи выпуклого программирования. Методы нелинейного программирования объединяют группу других методов, которые приспособлены для решения задач определенного класса. В частности, в такую группу могут входить градиентные методы, метод сканирования, метод случайного поиска, квадратичное и геометрическое программирование.Слайд 166. Стохастическое программирование
Стохастическое программирование позволяет решать
условно экстремальные задачи при неполной информации о параметрах и условиях
задачи и когда отдельные или многие показатели случайны (стохастичны). Если предыдущие результаты исследований или эксперимент позволяют установить вероятностные характеристики параметров процесса, то такие процессы называют процессами, связанными с риском. В тех случаях, когда вероятностные характеристики параметров процесса неизвестны, будем иметь дело с неопределенными процессами или явлениями. Нередко стохастические задачи заменяют эквивалентными детерминированными задачами математического программирования и используют для их решения разработанные вычислительные методы. Широкий круг задач стохастического программирования решают специальными методами, основанными на принципах стохастической аппроксимации и ее обобщений.Слайд 187. Принцип максимума
Принцип максимума чаще применяют для
оптимального управления процессом при наличии ограничений. Этот метод применяют для
нахождения экстремума непрерывной целевой функции, а также и для оптимизации дискретных задач. Принцип максимума позволяет получить решение в аналитической форме.Слайд 198. Экстремальное управление
Экстремальное управление обеспечивает достижение и
поддержание оптимальных значений параметров процесса. Это достигается с помощью управляющих
устройств (автоматических оптимизаторов). Применение таких устройств целесообразно для управления процессами, протекающими в сложных условиях при воздействии стохастических факторов. Оптимизатор автоматически производит поиск экстремума целевой функции и изменяет в нужную сторону управляющие факторы.Слайд 209. Графический метод
На
практике поиск оптимального значения не всегда может являться самоцелью решения
задачи. Необходимость учета не только экономических сторон требует принятия необязательно точно оптимального решения, соответствующего экстремуму целевой функции. Смежные с экстремумом значения могут несущественно отличаться от оптимального, но могут оказаться предпочтительней с иных позиций (социальных, конъюнктурных и др.), не поддающихся экономической оценке. С этих позиций нередко целесообразно бывает не заниматься аналитическими или численными методами поиска оптимальных значений, а применить традиционный графический метод, т.е. следует по уравнению целевой функции построить в соответствующих координатах график изменения этой функции в зависимости от переменных аргументов. Такие графики можно рассчитать, когда целевая функция задана в явном виде и количество переменных аргументов весьма незначительно.Слайд 21 Графическое изображение дает наглядное представление о характере
поведения целевой функции и позволяет получить с достаточной для практических
целей точностью ее численные значения во всем диапазоне изменения аргументов.9. Графический метод
Слайд 22Заключение
Тема моего проекта: «Применение математики в
поисках оптимального решения». Мы рассмотрели основные методы принятия решений для
оптимизации процессов в различных сферах деятельности человека. Осознали, что в наше время для облегчения сложных экономических ситуаций и процессов управления предприятием руководителям требуется некоторая основа и «доказанная гарантия» принимаемого решения. Неизбежно требуется формализация процесса принятия решений. Как правило, важные решения принимаются опытными людьми, довольно далекими от математики, и особенно от ее новых методов, и опасающимися больше потерять от формализации, чем выиграть.Слайд 23 Сегодня для выработки такого решения требуется
научный подход - слишком велики потери, связанные с ошибками. Оптимальные
решения позволяют обеспечить предприятию максимально выгодные условия выпуска продукции с наименьшими затратами на ее произведение.В данной работе я рассказала о важности правильного анализа, который впоследствии поможет принять рациональное решение в какой-либо отрасли деятельности.
Заключение
Слайд 24Список использованной литературы
Замков О.О., Толстопятенков А.В., Черемных Ю.И.. Математические методы
в экономике. М., ДИС, 1997г. – 368 с.
Малыхин В.И. Математика
в экономике. М., ИНФРА-М, 1999г. - 356с. Стойлова Л.П. Математика: Учеб. пособие для студ. высш. пед. учеб.заведений М.: Издательский центр «Академия», 2004. – 424 с.
Столл Р.Р. Множества. Логика. Аксиоматические теории. / Перевод с английского Гастева Ю.А. и Шмаина И.Х. под редакцией Шихановича Ю.А.. — М.: Просвещение, 1968. — 232 с
https://cyberleninka.ru/article/n/issledovanie-metodov-resheniya-zadach-nahozhdeniya-optimalnogo-resheniya-s-primeneniem-mnogih-kriteriev/viewer