Проективные преобразования в компьютерной графике

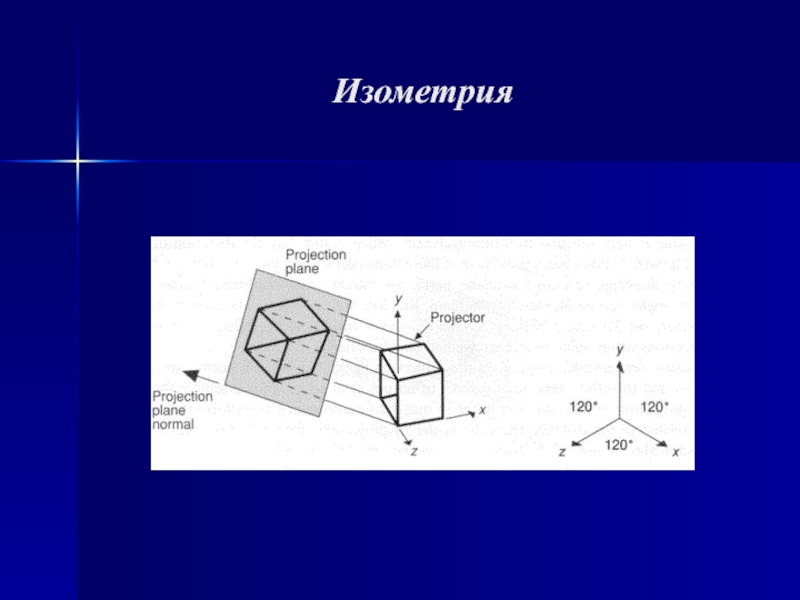
изобразить только проекции трехмерных объектов, а не сами объекты.
В общем

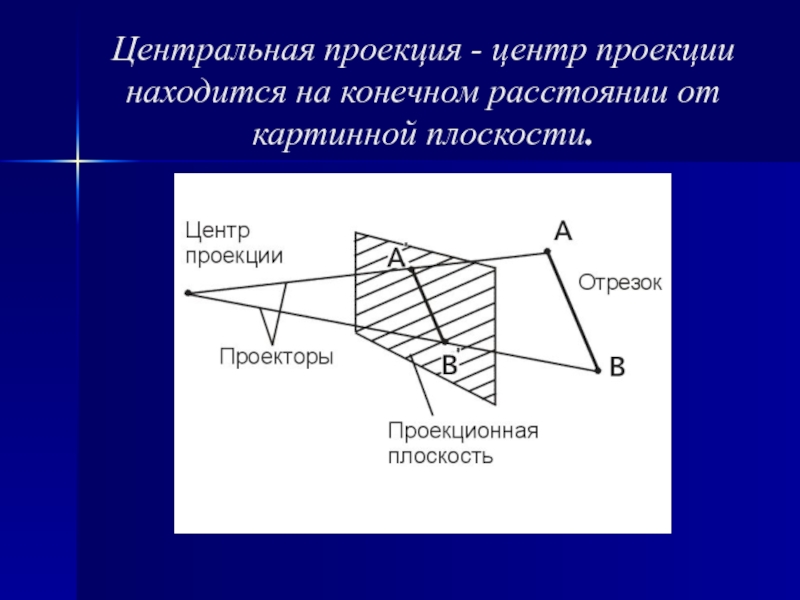
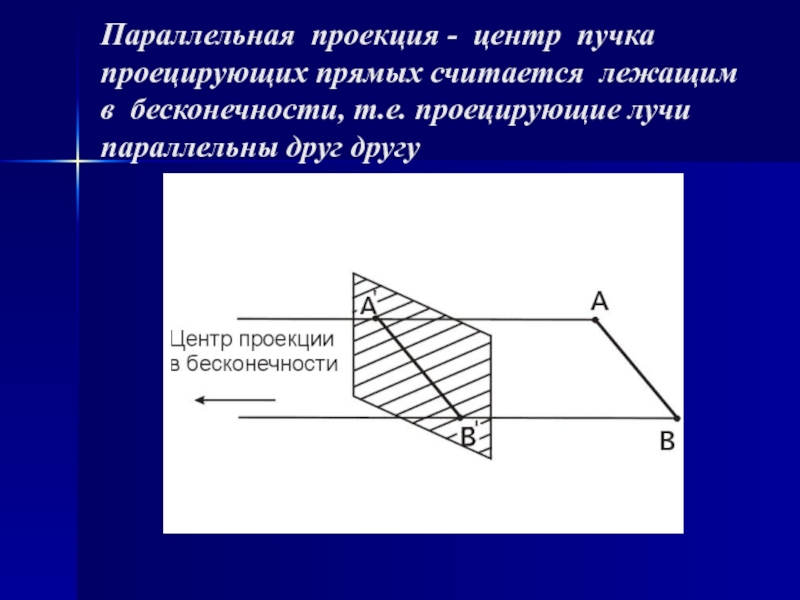
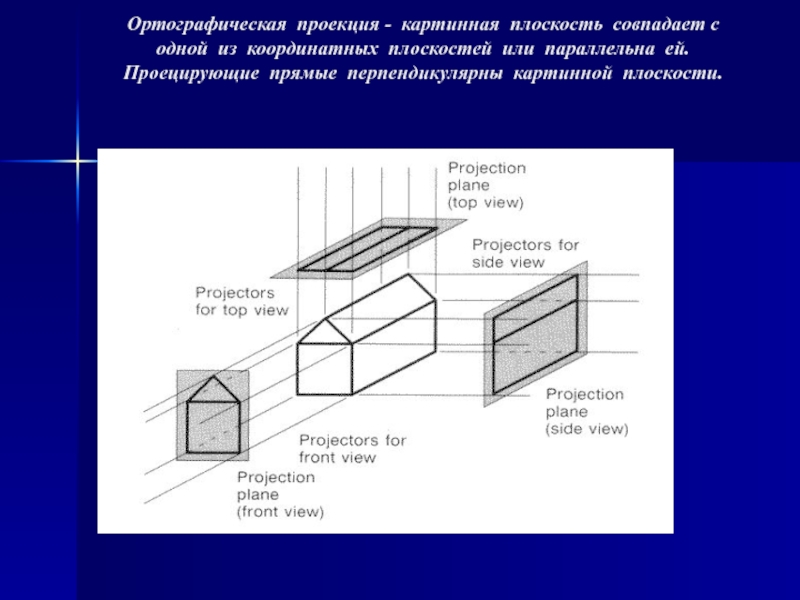
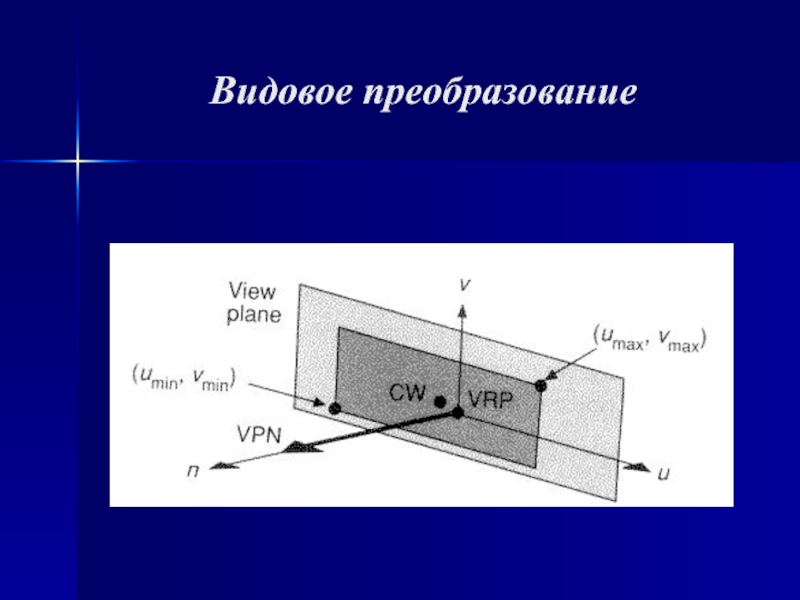
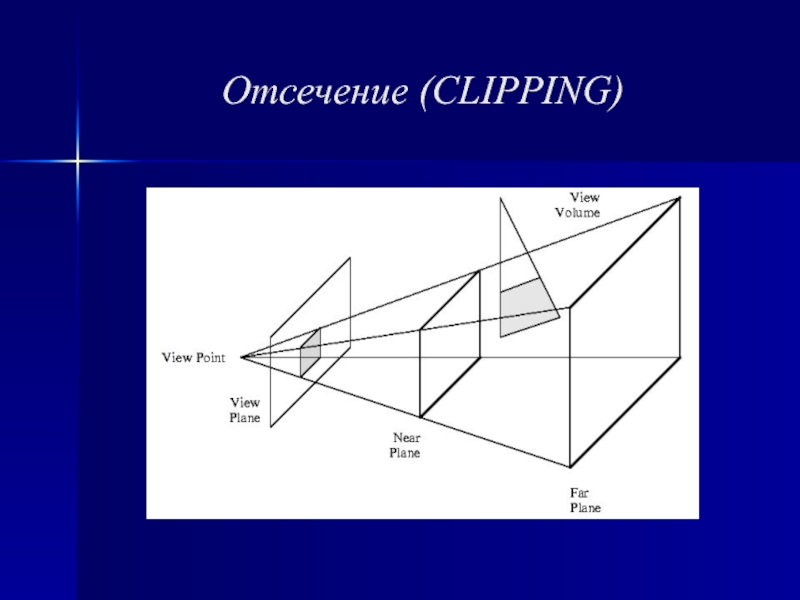
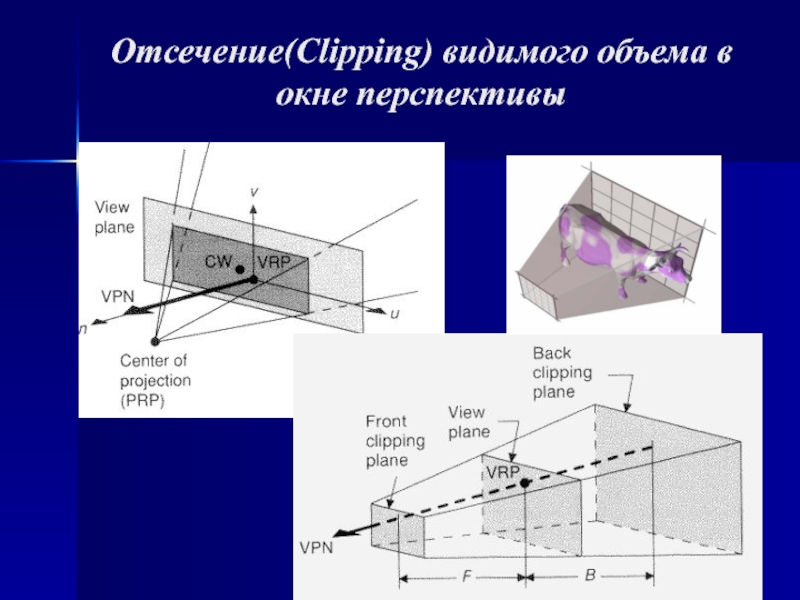
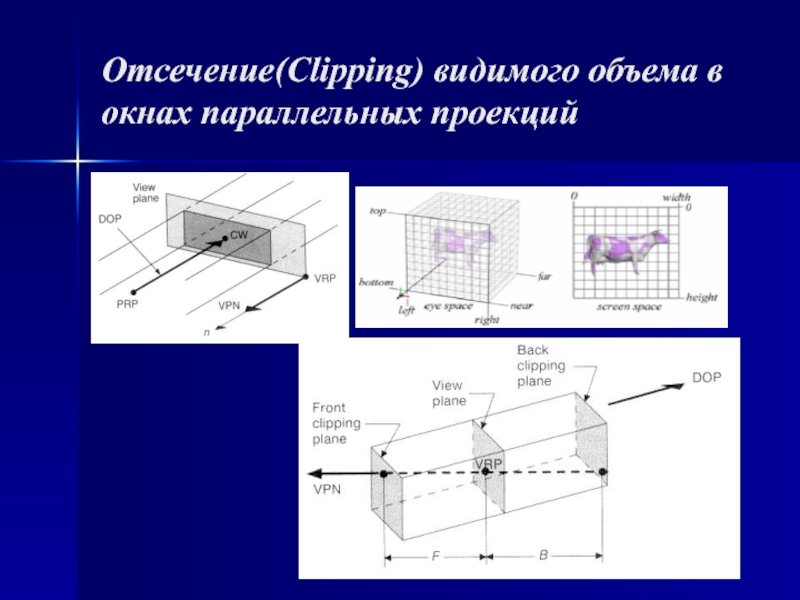
случае проекции преобразуют точки, заданные в системе координат размерностью n в точки системы координат размерностью меньшей, чем n. В нашем случае точки трехмерного пространства n=3 преобразуются в точки двумерного пространства n-1.

Задача состоит в том, чтобы определить проекцию каждой точки объекта, расположенного в произвольном месте трехмерного пространства, на некоторую плоскость в этом пространстве, называемую картинной плоскостью.

через каждую точку трехмерного объекта и затем проходят через картинную

плоскость и образуют тем самым проекцию.
Тип проецирования на плоскую, а не искривленную поверхность, где в качестве проекторов используются прямые, а не искривленные линии, называется плоской геометрической проекцией.
Плоские геометрические проекции делятся на два вида: центральные(перспективные) и параллельные.

картинной плоскости.

бесконечности, т.е. проецирующие лучи параллельны друг другу

косоугольные

плоскостей или параллельна ей. Проецирующие прямые перпендикулярны картинной плоскости.

сама картинная плоскость образует с осями координат ненулевые углы.
Если

все три угла различны между собой - проекция триметрическая;
если два угла из трех равны - проекция диметрическая;
если равны все три угла - проекция изометрическая.
Каждый из трех видов указанных проекций получается комбинацией поворотов, за которой следует параллельное проецирование.

картинной плоскости, называют косоугольными.
Однако сама картинная плоскость перпендикулярна главной

координатной оси, поэтому сторона объекта, параллельная этой плоскости, проецируется так, что можно измерять углы и расстояния.
Среди косоугольных проекций различают:
свободную проекцию(Cavalier), когда угол наклона проецирующих прямых к картинной плоскости равен половине прямого, т.е. 450,
кабинетную проекцию(Cabinet), когда требуется еще, чтобы масштаб по одной из осей был вдвое меньше, чем по двум остальным осям.

размером диафрагмы

не параллельны картинной плоскости будут сходиться в точке схода. Точка

схода называется главной если совокупность прямых параллельна одной из координатных осей. Имеется только 3 главные точки схода, соответствующие пересечениям главных координатных осей с картинной плоскостью. Т.о. перспективные проекции классифицируются в зависимости от числа главных точек схода и разделяются на одно-, двух- и трехточечные проекции.