Производная функции

дифференциала
Основные теоремы о дифференциалах
Применение дифференциала в приближенных вычислениях
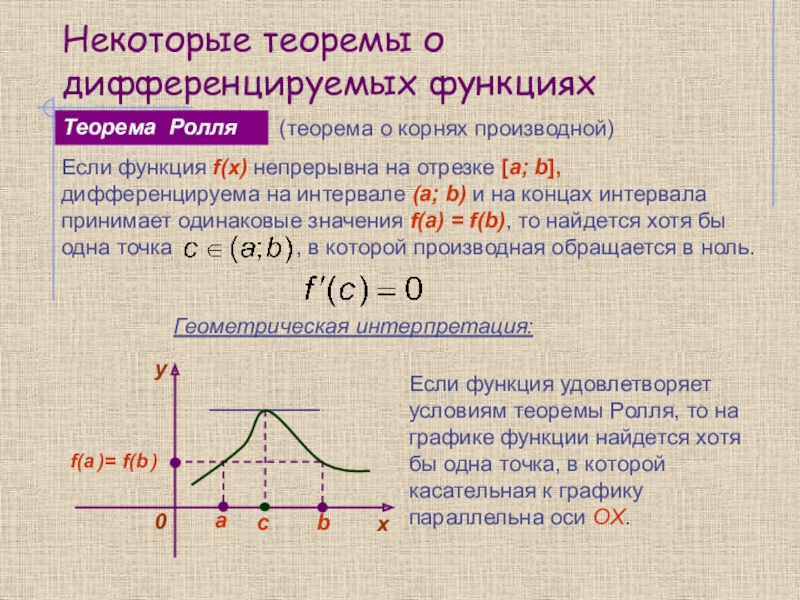
Некоторые теоремы о

ой производной) называется производная от производной n -1 - ого

Производная от производной второго порядка, если она существует называется производной третьего порядка и обозначается:

Итак:

, производные обозначаются римскими цифрами или цифрами в скобках:
Вычислить производную

находится по формуле:
Пусть функция y = f(x) задана параметрически уравнениями:
Найдем

Аналогично получаем:

и т. д.

от функции:

х отличную от нуля производную, следовательно существует предел:
где
при
По теореме о

главная часть ее приращения:
Дифференциал независимой переменной равен приращению этой переменной
Поэтому:

Дифференциал функции равен произведению производной функции на дифференциал независимой переменной

точке М(x, y) касательную
х
f(x )
x+Δx
М
М1
f(x+ Δx )
Рассмотрим ординату касательной для

Согласно геометрическому смыслу производной,

B

A

Из прямоугольного треугольника AВМ имеем:

Дифференциал функции y = f(x) в точке x равен приращению ординаты касательной к графику функции в этой точке, когда x получает приращение Δx.

Дифференциал суммы, разности, произведения

Теорема 2

Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.

Это свойство дифференциала называют инвариантностью (неизменностью) формы дифференциала.

в виде:

Это равенство позволяет с большой точностью вычислять приращение любой дифференцируемой функции.

Подставим в равенство выражения для приращения и дифференциала функции:

Формула позволяет приближенно вычислять значение функции в точке x0+Δx, зная значение функции в точке x0.

0

0

0

Геометрическая интерпретация:
Если функция удовлетворяет

(теорема о корнях производной)

(теорема об отношении приращений)
Теорема

(теорема о конечных приращениях)

На графике функции найдется хотя бы одна точка, в которой касательная параллельна хорде AB

применении производной.
то
Теорема справедлива также в случае, если