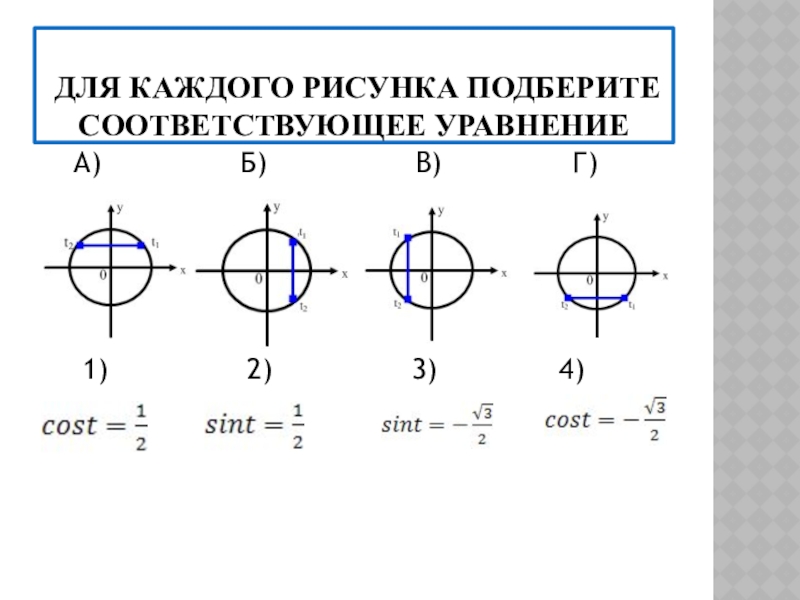
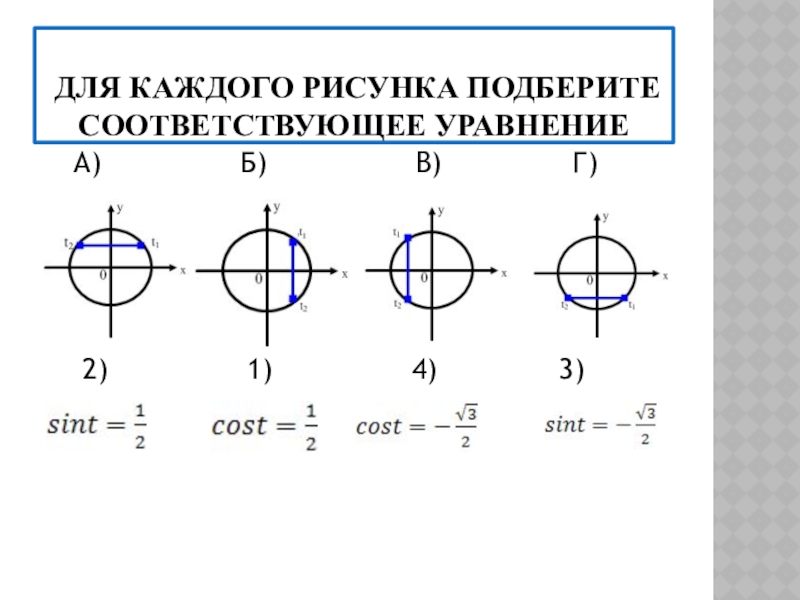
числовой окружности;
2) уметь определять значения синуса, косинуса, тангенса и котангенса
для координат точек числовой окружности;3) знать свойства основных тригонометрических функций;
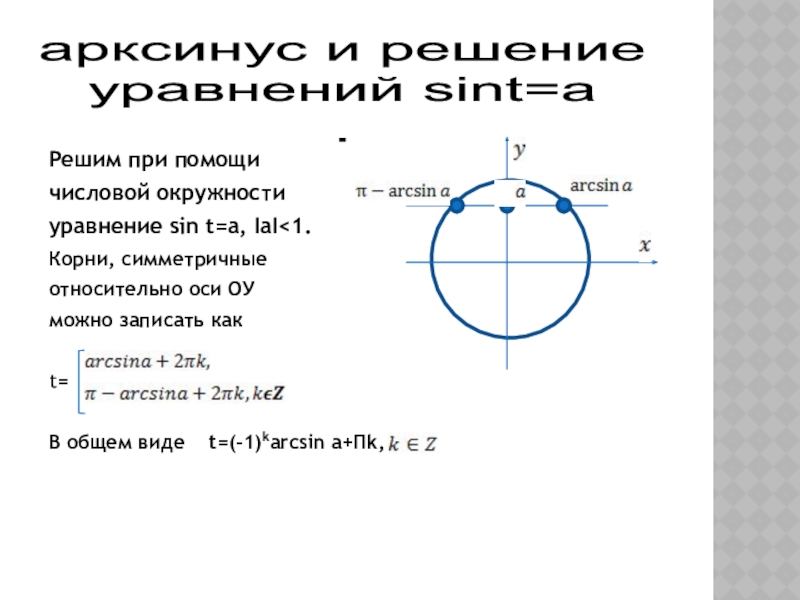
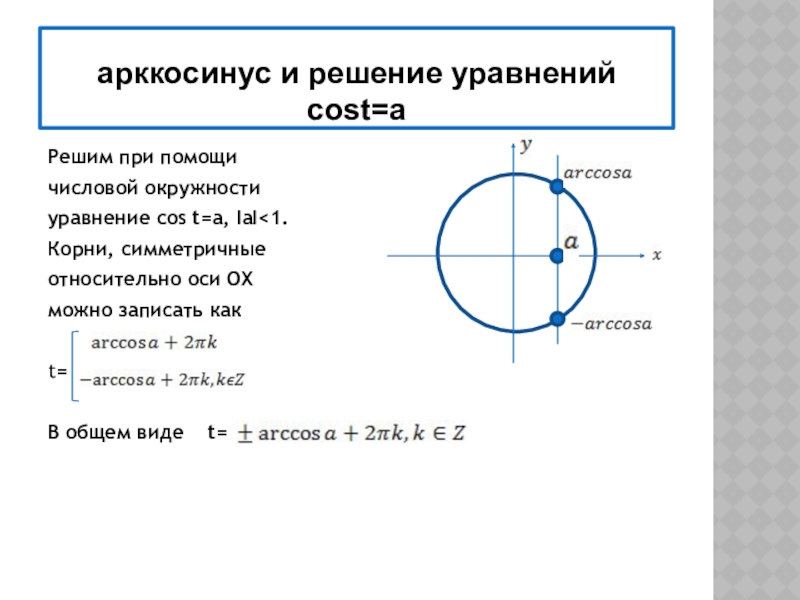
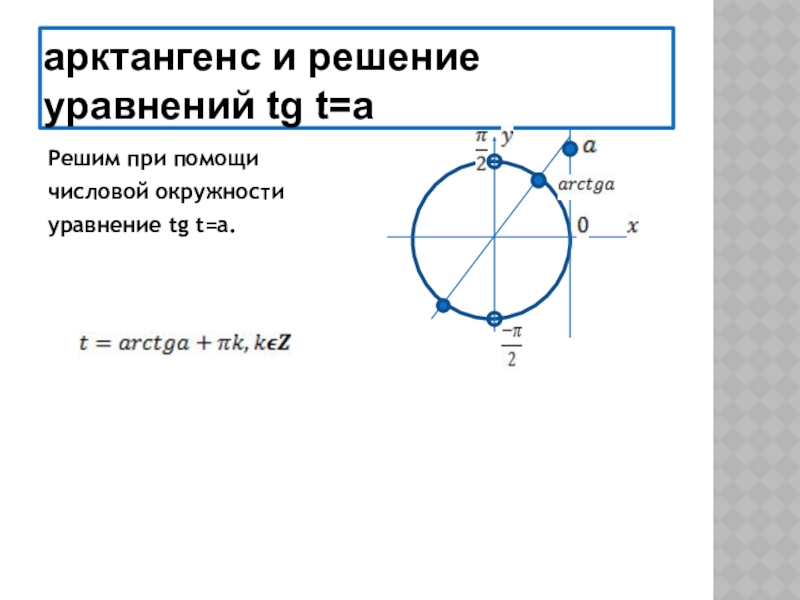
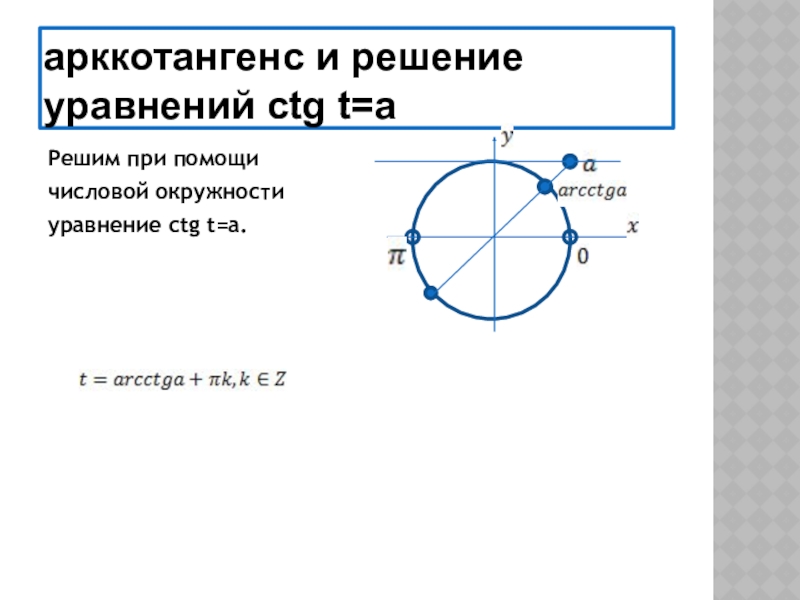
4) знать понятие арксинуса, арккосинуса, арктангенса, арккотангенса и уметь отмечать их на числовой окружности.