Слайд 1Процессы на поверхности раздела твердое тело -газ
НТ-10
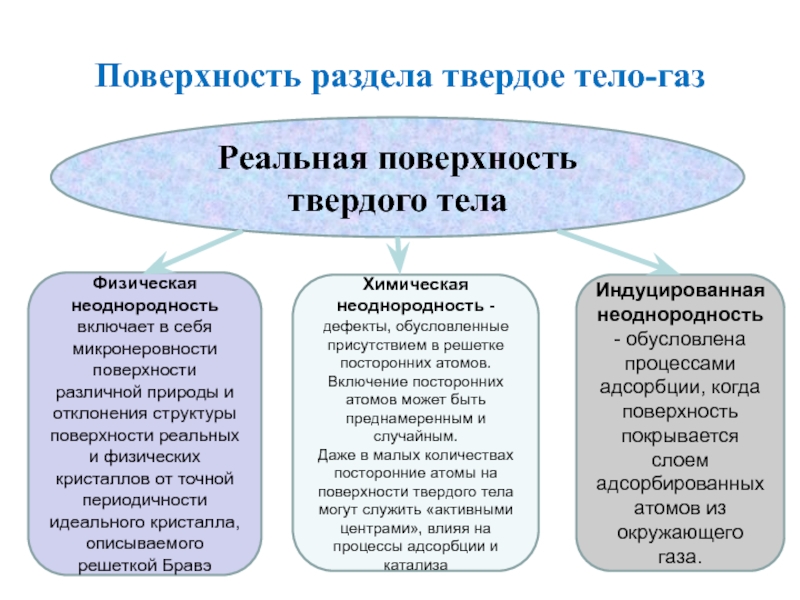
Слайд 2Поверхность раздела твердое тело-газ
Реальная поверхность твердого тела
Физическая неоднородность включает в
себя микронеровности поверхности различной природы и отклонения структуры поверхности реальных
и физических кристаллов от точной периодичности идеального кристалла, описываемого решеткой Бравэ
Химическая неоднородность -дефекты, обусловленные присутствием в решетке посторонних атомов.
Включение посторонних атомов может быть преднамеренным и случайным.
Даже в малых количествах посторонние атомы на поверхности твердого тела могут служить «активными центрами», влияя на процессы адсорбции и катализа
Индуцированная неоднородность- обусловлена процессами адсорбции, когда поверхность покрывается слоем адсорбированных атомов из окружающего газа.
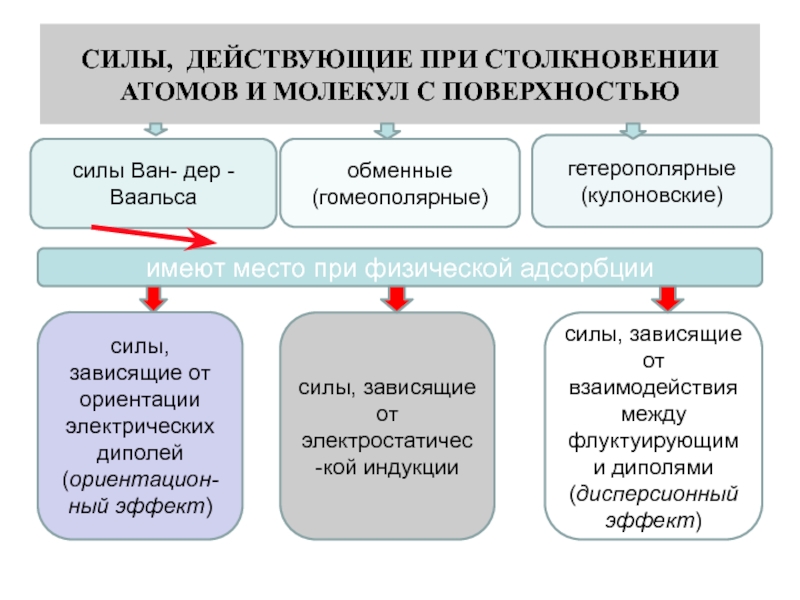
Слайд 3СИЛЫ, ДЕЙСТВУЮЩИЕ ПРИ СТОЛКНОВЕНИИ АТОМОВ И МОЛЕКУЛ С ПОВЕРХНОСТЬЮ
силы
Ван- дер -Ваальса
обменные (гомеополярные)
гетерополярные (кулоновские)
имеют место при физической адсорбции
силы, зависящие
от электростатичес-кой индукции
силы, зависящие от ориентации электрических диполей (ориентацион-ный эффект)
силы, зависящие от взаимодействия между флуктуирующими диполями (дисперсионный эффект)
Слайд 5СИЛЫ, ДЕЙСТВУЮЩИЕ ПРИ СТОЛКНОВЕНИИ АТОМОВ И МОЛЕКУЛ С ПОВЕРХНОСТЬЮ
ОБМЕННЫЕ СИЛЫ
при
слабой хемосорбции на однородных и неоднородных поверхностях
Переход от действия сил
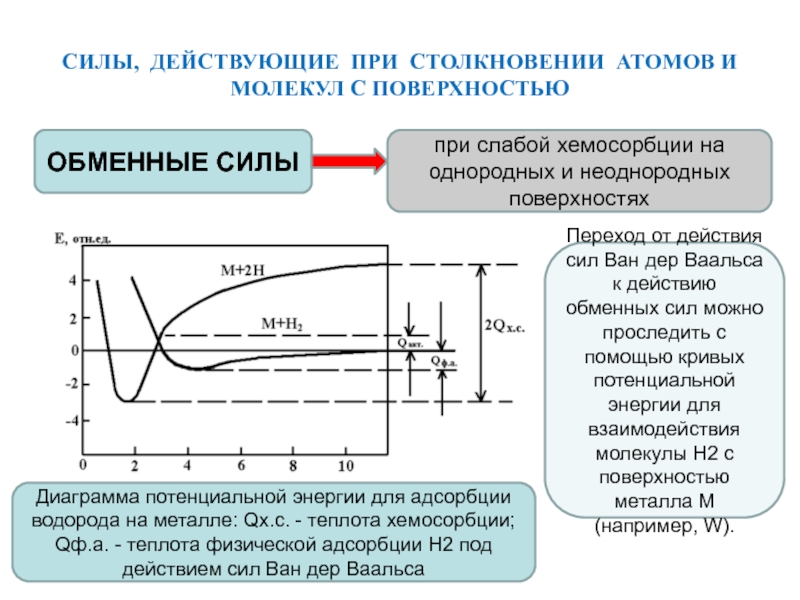
Ван дер Ваальса к действию обменных сил можно проследить с помощью кривых потенциальной энергии для взаимодействия молекулы H2 с поверхностью металла М (например, W).
Диаграмма потенциальной энергии для адсорбции водорода на металле: Qх.с. - теплота хемосорбции; Qф.а. - теплота физической адсорбции Н2 под действием сил Ван дер Ваальса
Слайд 6СИЛЫ, ДЕЙСТВУЮЩИЕ ПРИ СТОЛКНОВЕНИИ АТОМОВ И МОЛЕКУЛ С ПОВЕРХНОСТЬЮ
По мере
приближения молекулы Н2 к поверхности металла она может быть адсорбирована
«физически», так что взаимодействие будет описываться кривой М + Н2 .
Если молекула получает некоторую энергию активации Qакт. (эта энергия может быть очень мала и даже равна нулю), то система может перейти на потенциальную кривую М + 2Н , на которой (после диссоциации молекулы водорода на атомы) ее атомные составляющие становятся слабо хемосорбированными.
Такая слабая хемосорбция характеризуется тем, что в противоположность случаю сил связи Ван дер Ваальса электронная оболочка адсорбированного атома может проникать в электронную оболочку металла.
Слайд 7СИЛЫ, ДЕЙСТВУЮЩИЕ ПРИ СТОЛКНОВЕНИИ АТОМОВ И МОЛЕКУЛ С ПОВЕРХНОСТЬЮ
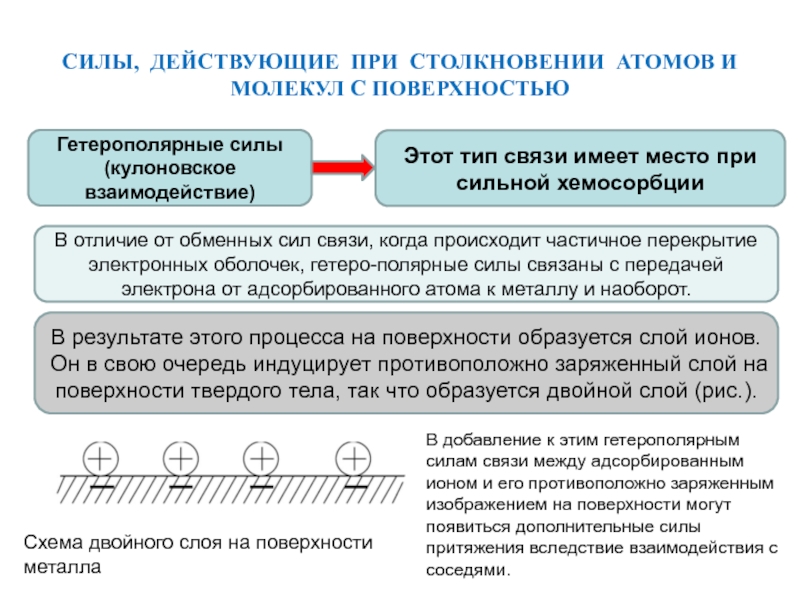
Гетерополярные силы
(кулоновское взаимодействие)
Этот тип связи имеет место при сильной хемосорбции
В отличие
от обменных сил связи, когда происходит частичное перекрытие электронных оболочек, гетеро-полярные силы связаны с передачей электрона от адсорбированного атома к металлу и наоборот.
В результате этого процесса на поверхности образуется слой ионов. Он в свою очередь индуцирует противоположно заряженный слой на поверхности твердого тела, так что образуется двойной слой (рис.).
Схема двойного слоя на поверхности металла
В добавление к этим гетерополярным силам связи между адсорбированным ионом и его противоположно заряженным изображением на поверхности могут появиться дополнительные силы притяжения вследствие взаимодействия с соседями.
Слайд 8Адсорбция
Поверхностная энергия стремится к самопроизвольному уменьшению. Это выражается в уменьшении
межфазной поверхности или поверхностного натяжения:
Gs = σ·S
К явлениям, происходящим к
вследствие стремления к самопроизвольному снижению поверхностного натяжения, относится адсорбция.
На любой границе раздела существует «поверхностный слой» (ПС) – переходная область от одной объемной фазы к другой.
Поверхностный слой имеет очень малую толщину (всего несколько молекул), но в нем сосредоточен весь избыток поверхностной энергии и массы вещества.
Слайд 9Адсорбция
АДСОРБЦИЯ
процесс самопроизвольного перераспределения компонентов системы между поверхностным слоем и объемной
фазой
С термодинамической точки зрения адсорбция – самопроизвольный процесс выравнивания химических
потенциалов в объеме системы и в межфазном (приповерхностном) слое
Этот процесс происходит вследствие стремления к минимуму поверхностной энергии или энергии Гиббса системы.
Слайд 10Основные термины и определения
Адсорбция — процесс самопроизвольного перераспределения вещества между
поверхностным слоем и объемом фазы.
Основные закономерности адсорбции
Правило выравнивания полярностей
(
П. А. Ребиндер )
Вещество может адсорбироваться на поверхности раздела фаз, если его присутствие в межфазном слое уравнивает разность полярностей этих фаз в зоне их контакта.
Слайд 11∆G= ∆Н - Т∆S ‹ 0
При адсорбции
происходит самопроизвольное снижение удельной свободной поверхностной энергии (поверхностного натяжения).
Количественные
характеристики адсорбции
Избыточная гиббсовская адсорбция (Г ) – избыток адсорбата в поверхностном слое по сравнению с его количеством в объеме фазы, отнесенный к единице площади поверхности или единице массы адсорбента (моль/м2; моль/г), характеризует адсорбцию на жидкой поверхности.
Абсолютная адсорбция (а) – количество адсорбата на единице массы или поверхности адсорбента (моль/г; моль/м2), используется для характеристики адсорбции на твердой поверхности.
∆Н – теплота адсорбции (мера интенсивности взаимодействия адсорбата с поверхностью адсорбента).
Слайд 12Еще несколько терминов
Адсорбентом называют вещество, на котором происходит адсорбция;
Адсорбатом
называют уже адсорбированное вещество, находящееся на поверхности или в объеме
пор адсорбента;
Адсорбтивом называют вещество, способное адсорбироваться, но еще не адсорбированное.
Допускается (когда различия между адсорбцией и абсорбцией малы или механизм поглощения не ясен) использование более общих терминов сорбция, сорбент, сорбат, сорбтив.
Два предельных случая адсорбции: адсорбцию химическую или хемосорбцию и физическую или физадсорбцию.
Слайд 13Адсорбция на твердом теле
Примеры
Физическая адсорбция: адсорбция аммиака на угле.
Химическая адсорбция:
адсорбция углекислого газа на извести.
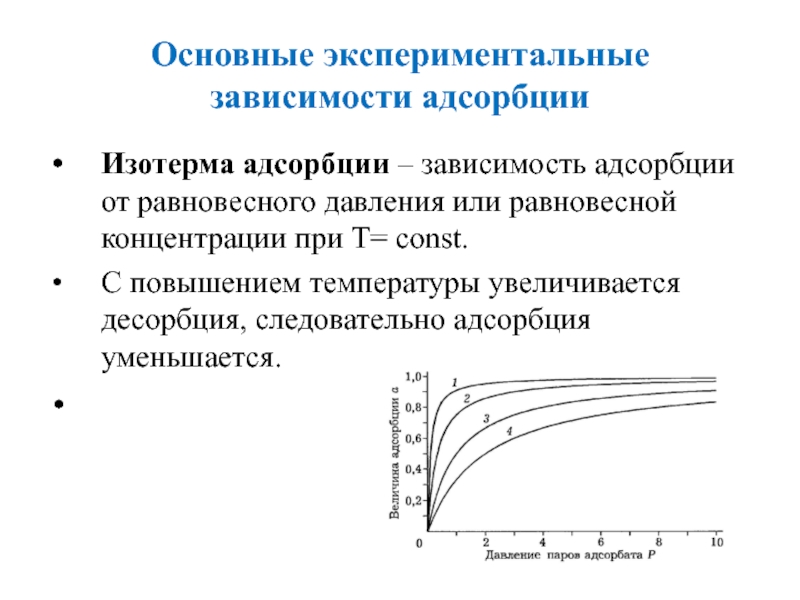
Слайд 14Основные экспериментальные зависимости адсорбции
Изотерма адсорбции – зависимость адсорбции от равновесного
давления или равновесной концентрации при Т= const.
С повышением температуры увеличивается
десорбция, следовательно адсорбция уменьшается.
Слайд 15Основные экспериментальные зависимости адсорбции
Изобара (изопикта) адсорбции – зависимость адсорбции от
температуры при постоянной концентрации или давлении (С,р = const).
Рис.- Типовые
изобары : а- хемосорбции; б- физадсорбции.
Слайд 16Основные экспериментальные зависимости адсорбции
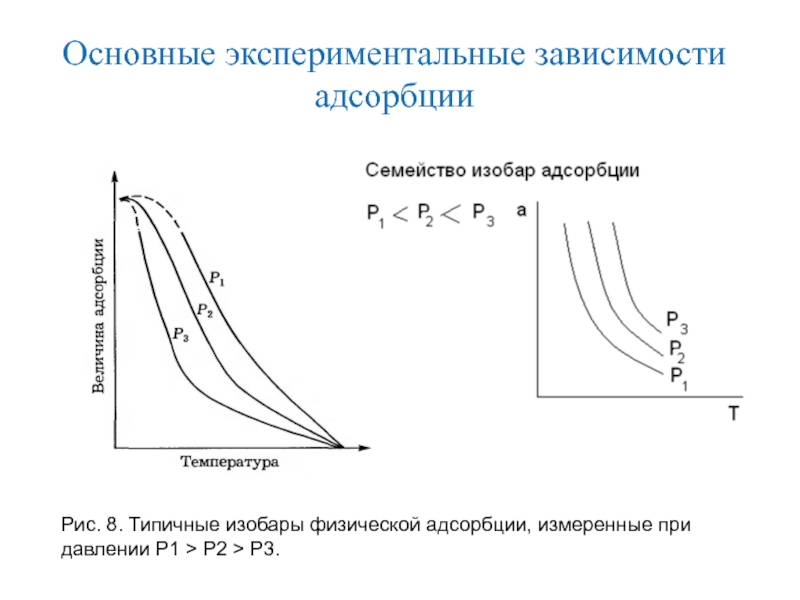
Рис. 8. Типичные изобары физической адсорбции, измеренные
при давлении Р1 > Р2 > Р3.
Слайд 17Основные экспериментальные зависимости адсорбции
Изостера адсорбции – зависимость концентрации или парциального
давления от температуры при постоянной величине адсорбции А= const (расчетная
зависимость, позволяющая определить теплоту адсорбции).
Наиболее распространенной зависимостью, получаемой экспериментально, является изотерма адсорбции, так как проще всего обеспечить постоянство температуры.
Слайд 18Основные экспериментальные зависимости адсорбции
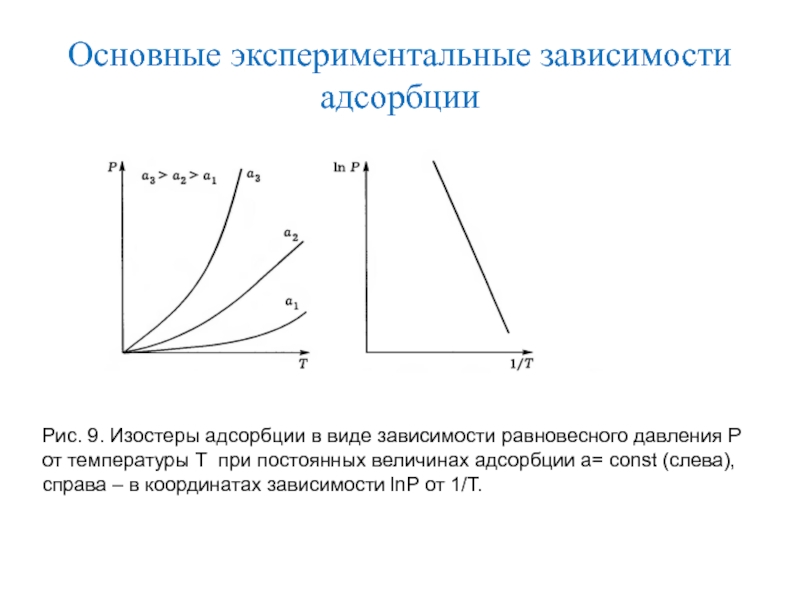
Рис. 9. Изостеры адсорбции в виде зависимости
равновесного давления Р от температуры Т при постоянных величинах адсорбции
а= const (слева), справа – в координатах зависимости lnP от 1/Т.
Слайд 19ОСНОВНЫЕ ПОНЯТИЯ
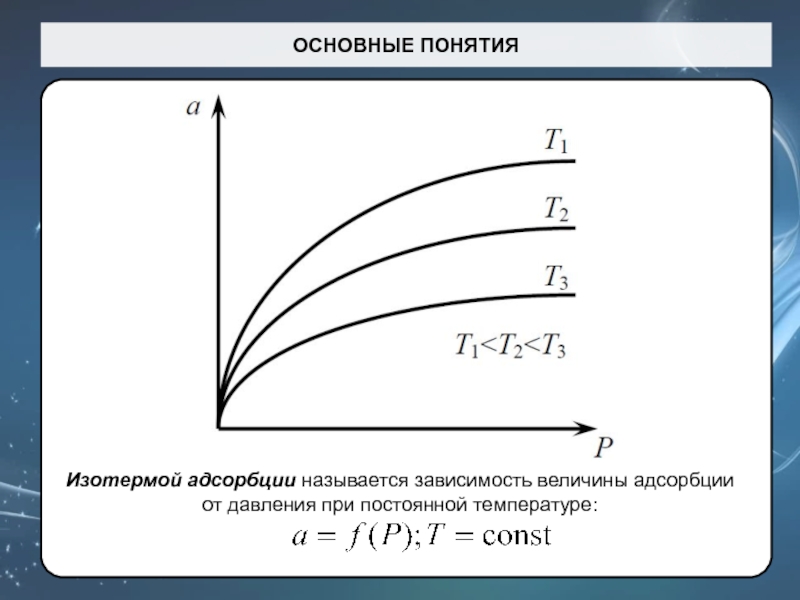
Изотермой адсорбции называется зависимость величины адсорбции от давления при
постоянной температуре:
Слайд 20Изотерма адсорбции Генри
Простейшее уравнение изотермы адсорбции, называемой изотермой (законом) Генри
записывается в виде:
Г = Кг P
Это уравнение применимо при максимальных заполнениях поверхности и малых давлениях, когда газ можно рассматривать как идеальный, а число соударений его молекул с поверхностью, не занятой другими адсорбированными молекулами, n пропорционально Р.
Величина адсорбции Г отнесена к единице поверхности, а коэффициент пропорциональности Кг, обычно называют константой Генри. Формально Кг можно рассматривать как константу термодинамического равновесия:
Кг =Г/Р,
особенность которой в том, что она является смешанной, поскольку содержит давление Р и величину Г – эквивалент концентрации.
Название уравнения и его константы связано с именем выдающегося английского физхимика Уильяма Генри (1774-1836), сделавшего большой вклад в исследования свойств газов, и из-за формальной аналогии между этим законом и открытым У.Генри в 1808 г. законом растворимости газов в жидкостях.
Слайд 21Изотерма адсорбции Генри
Это уравнение - предельная форма всех теоретических изотерм
адсорбции при Р→0 и основа стандартизации термодинамических функций, характеризующих адсорбцию.
Но этот закон строго выполняется только при малых давлениях и малых степенях заполнения (покрытия) поверхности.
При этом степень заполнения поверхности обычно определяется как ϴ = Г/Гмах,
где Гмах - предельное содержание молекул на единице поверхности в заполненном монослое.
Слайд 22Изотерма адсорбции Ленгмюра
Это уравнение изотермы, описывающее ситуации при больших
покрытиях, предложено в 1916 г. выдающимся американским ученым Ирвингом Ленгмюром
(1881-1957), лауреатом Нобелевской премии 1932 г. По смыслу вывода, это уравнение локализованной мономолекулярной адсорбции на однородной поверхности, полученное без учета взаимодействия адсорбат - адсорбат.
Слайд 23Допущения Легмюра:
1) поверхность твердого тела состоит из элементарных участков (адсорбционных
центров).
2) каждый адсорбционный центр может адсорбировать только одну молекулу газа.
3)
адсорбционные центры энергетически эквивалентны (имеют одинаковое сродство к молекулам газа).
4) адсорбированные молекулы не взаимодействуют между собой и не могут перемещаться в поверхностном слое.
В таких условиях образуется мономолекулярный слой адсорбированных молекул.
Теория мономолекулярной адсорбции Ленгмюра.
Изотерма адсорбции Ленгмюра.
1. Адсорбция на границе твердое тело – газ
На поверхности твердого тела лучше адсорбируются те газы, которые легче конденсируются в жидкость. Например, активированный уголь хорошо адсорбирует аммиак (Ткип.=240 К), но не адсорбирует оксид углерода (II) (Ткип=83 К).
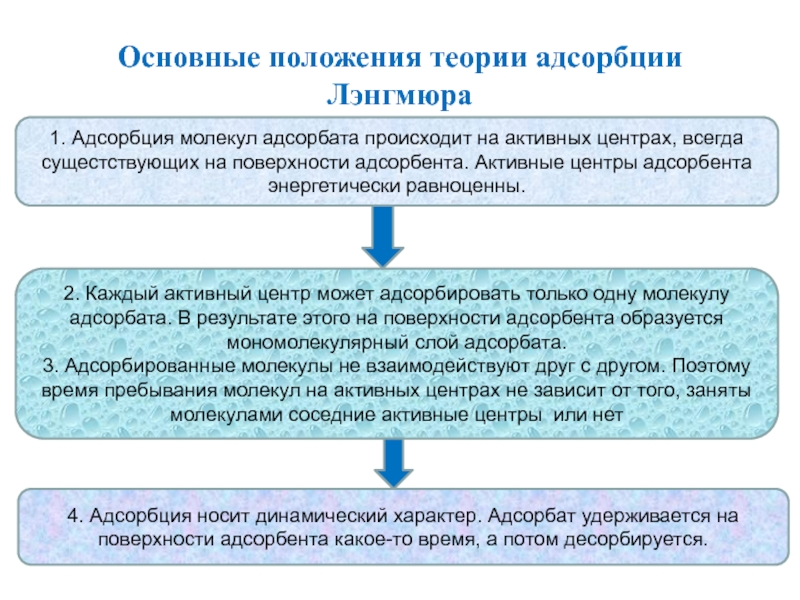
Слайд 24Основные положения теории адсорбции Лэнгмюра
1. Адсорбция молекул адсорбата происходит на
активных центрах, всегда сущестствующих на поверхности адсорбента. Активные центры адсорбента
энергетически равноценны.
2. Каждый активный центр может адсорбировать только одну молекулу адсорбата. В результате этого на поверхности адсорбента образуется мономолекулярный слой адсорбата.
3. Адсорбированные молекулы не взаимодействуют друг с другом. Поэтому время пребывания молекул на активных центрах не зависит от того, заняты молекулами соседние активные центры или нет
4. Адсорбция носит динамический характер. Адсорбат удерживается на поверхности адсорбента какое-то время, а потом десорбируется.
Слайд 25Изотерма адсорбции Ленгмюра
Для вывода этого уравнения рассмотрим квазихимическую реакцию
между молекулой адсорбата M и активным центром Z на поверхности
адсорбента
M + [ Z ] = [MZ] (1)
где [MZ]- локализованный адсорбционный комплекс. Если пренебречь взаимодействием адсорбат - адсорбат и влиянием образовавшихся адсорбционных комплексов на соседние активные центры и полагать, что число свободных центров на поверхности составляет долю (1-ϴ) от общего числа центров, а число занятых центров - долю ϴ, то константа равновесия этой реакции
К = ϴ/Р( 1-ϴ) (2)
Из (2) следует :
ϴ= КР/( 1 + К ·Р) = Г/Гмах (3)
или
Г= Гмах К ·Р/ [ 1 + К Р ] (4)
Слайд 26Изотерма адсорбции Ленгмюра
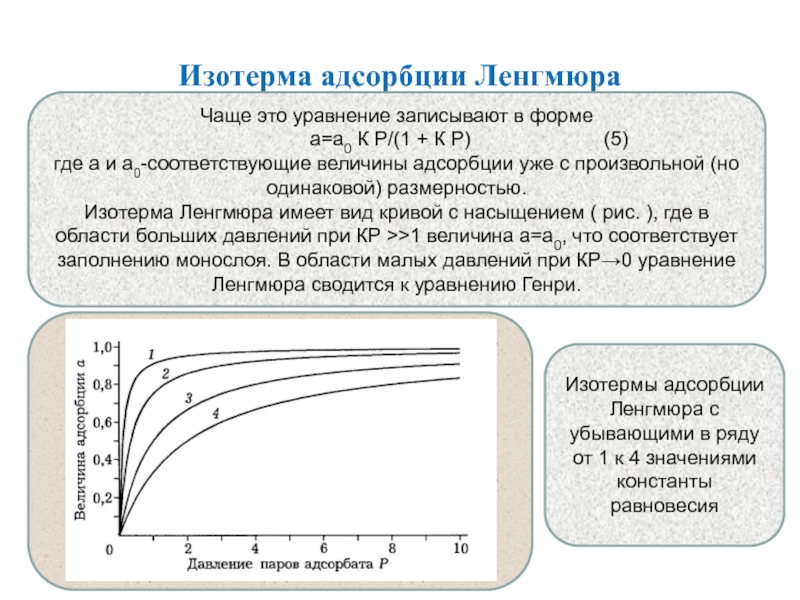
Чаще это уравнение записывают в форме
а=а0
К Р/(1 + К Р) (5)
где а и а0-соответствующие величины адсорбции уже с произвольной (но одинаковой) размерностью.
Изотерма Ленгмюра имеет вид кривой с насыщением ( рис. ), где в области больших давлений при КР >>1 величина а=а0, что соответствует заполнению монослоя. В области малых давлений при КР→0 уравнение Ленгмюра сводится к уравнению Генри.
Изотермы адсорбции Ленгмюра с убывающими в ряду от 1 к 4 значениями константы равновесия
Слайд 27Изотерма адсорбции Ленгмюра
Уравнение Ленгмюра широко используется на практике. Для
расчета значений а0 и константы равновесия К оно записывается в
линейном виде как:
Р/а = 1/(а0К) + ( 1/а ) Р (6)
или:
а/Р = К а0 - К а (7)
или:
1/а = 1/а0 + ( 1/а0 К) ( 1/Р ) (8)
Константа адсорбционного равновесия К, подобно константам равновесия реакций в газах или растворах, связана со стандартным изменением изохорного потенциала уравнением:
∆F0 =∆U0- T ∆ S0 = - RT ln K (9)
откуда следует
К =e S0/R e-U0/RT =g eQ/RT (10)
где g- энтропийный множитель, Q- теплота адсорбции.
Слайд 28Характеристика уравнения
Лэнгмюра:
1. Имеет теоретическое обоснование;
2. Применимо для подвижной и
неподвижной границ раздела фаз;
3. Справедливо для малых и
больших концентраций
адсорбтива.
Уравнение адсорбции Лэнгмюра.
Г – адсорбция, моль/м2;
Г∞ – предельная адсорбция, моль/м2;
С – равновесная концентрация вещества, моль/дм3;
Р – равновесное давление вещества, Кпа,
К – константа адсорбционного равновесия.
Слайд 29Уравнение Фрейндлиха.
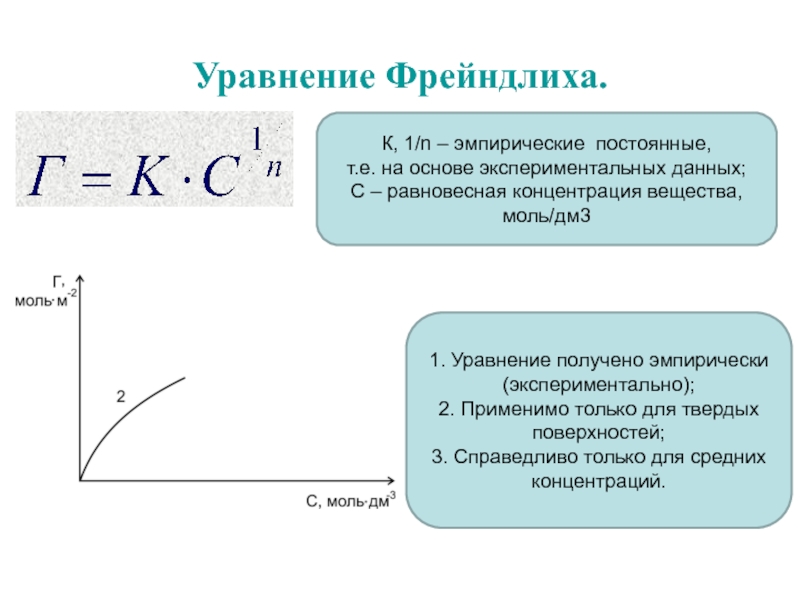
К, 1/n – эмпирические постоянные,
т.е. на основе экспериментальных данных;
С – равновесная концентрация вещества, моль/дм3
1. Уравнение получено эмпирически (экспериментально);
2.
Применимо только для твердых поверхностей;
3. Справедливо только для средних концентраций.
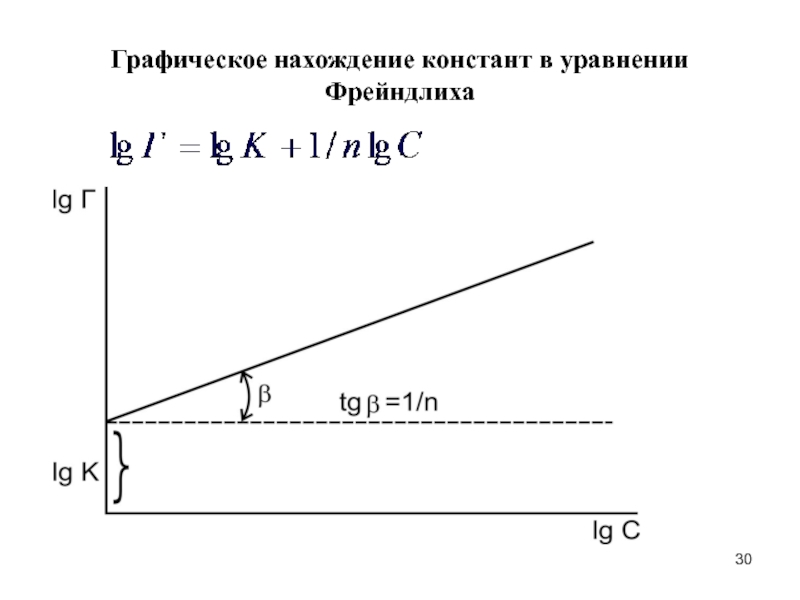
Слайд 30Графическое нахождение констант в уравнении Фрейндлиха
Слайд 31Другие уравнения мономолекулярной локализованной адсорбции
Уравнение Ленгмюра и его модификации
описывают локализованную мономоле-кулярную адсорбцию на однородной поверхности, которая не осложнена
взаимодействием адсорбированных компонентов между собой.
При наличии такого взаимодействия и тех же прочих условиях используется уравнение Фаулера-Гугенгейма:
Р = [/K(1-)] exp[-K1/RT] (11)
Слайд 32Другие уравнения мономолекулярной локализованной адсорбции
Уравнение Фаулера-Гугенгейма:
Р = [ϴ/K(1-ϴ)] exp[-K1ϴ/RT]
(11)
где первый член в квадратных скобках - уравнение Ленгмюра с
константой К, характеризующей взаимодействие адсорбат-адсорбент, а константа К1 в экспоненте характеризует межмолекулярное взаимодействие адсорбат - адсорбат в монослое.
(в свою очередь, константа К - аналог константы Генри и характеризует взаимодействие адсорбат - адсорбент).
Слайд 33Другие уравнения мономолекулярной локализованной адсорбции
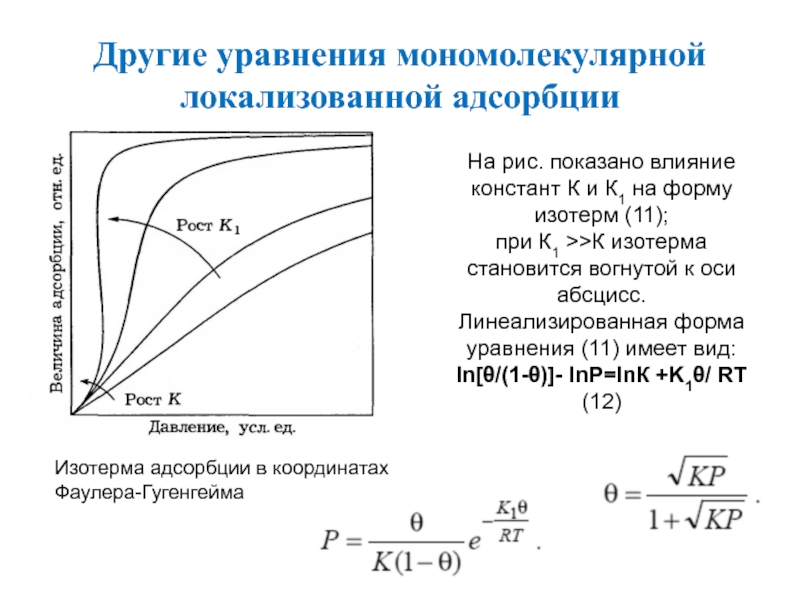
Изотерма адсорбции в координатах
Фаулера-Гугенгейма
На рис.
показано влияние констант К и К1 на форму изотерм (11);
при К1 >>К изотерма становится вогнутой к оси абсцисс.
Линеализированная форма уравнения (11) имеет вид:
ln[/(1-)]- lnP=lnК +K1/ RT (12)
Слайд 34Другие уравнения мономолекулярной локализованной адсорбции
Среди других уравнений изотерм адсорбции на
однородной поверхности, учитывающих взаимодействие адсорбат–адсорбат, отметим уравнение, которое предложено А.В.
Киселевым в форме: Р = ϴ/К(1-ϴ)(1+ К1ϴ)
с тем же смыслом констант, что и уравнение
Фаулера–Гугенгейма.
Слайд 35Другие уравнения мономолекулярной локализованной адсорбции
Дальнодействие сил при физической адсорбции обуславливает
образование нескольких слоев адсорбированных молекул. Заполнение второго слоя маловероятно до
тех пор, пока на поверхности находятся только отдельные изолированные молекулы, т.к. силы взаимодействия между единичной адсорбированной молекулой и ударяющейся о нее молекулой обычно малы по сравнению с силами на поверхности адсорбента, где в взаимодействии одновременно участвует большое число молекул.
Но по мере увеличения поверхностной концентрации адсорбата возрастает вероятность одновременного взаимодействия ударяющейся молекулы адсорбтива с 3, 4 и более адсорбированными ранее молекулами. “Время жизни” τ возрастает до значений, при которых на отдельных участках поверхности может начинаться полимолекулярная адсорбция.
Слайд 36Полимолекулярная адсорбция
Простейшее уравнение полимолекулярной адсорбции, полученное независимо на основе разных
предпосылок разными авторами и обычно называемое уравнением Френкеля-Хелси-Хилла (сокращенно ФХХ),
имеет вид:
ϴ= В1 (RTln(P/P0) -n (13)
или
t = B2 (RTln(P/P ) -n (14)
где t- среднестатистическая толщина полимолекулярной пленки адсорбата на поверхности адсорбента, получаемая делением объема адсорбата на величину поверхности адсорбента (при расчете объема адсорбата его плотность часто отождествляется с плотностью нормальной жидкой фазы).
Френкель и Хилл вывели это уравнение путем интегрировавания выражений для дисперсионного потенциала без учета сил отталкивания, действие которых во втором и последующих монослоях становится пренебрежимо малым.
В этом случае величина показателя степени n=3, а значения констант определяются из констант взаимодействия.
Слайд 37Полимолекулярная адсорбция
Хелси получил подобное уравнение эмпирически, анализируя изотермы адсорбции азота
при 77К на непористых системах, величина показателя степени оказалась близкой
~2.75.
Эти уравнения обычно используется при анализе распределения пор по размерам по данным капиллярно-конденсационных измерений .
Гораздо чаще на практике, в основном для измерений удельной поверх-ности, используется другое уравнение полимолекулярной адсорбции, называемое по имени авторов уравнением БЭТ- т.е уравнением Брунауэра, Эмметта, Теллера
( опубликовано в 1938 году).
Уравнение Френкеля-Хелси-Хилла, записанное в форме t=5.27ln(P/P0) -0.3109
Слайд 38Уравнение БЭТ
При выводе этого уравнения использованы допущения Ленгмюра:
рассматривается адсорбция
на однородной поверхности без учета взаимодействия между молекулами в плоскости
слоя,
но дополнительно вводится учет «вертикальных» межмолекулярных взаимодействий адсорбат–адсорбат.
3. Предполагается, что ударяющиеся молекулы, попадая на уже занятые места, не покидают их немедленно, а образуют адсорбционные комплексы из групп молекул.
4. По мере приближения к давлению насыщения Р0 сначала сокращается число свободных мест, а затем мест, занятых комплексами из одной, двух, трех и т.д. молекул.
Слайд 39Уравнение БЭТ полимолекулярной адсорбции
Рассмотрим такую полимолекулярную адсорбцию как серию квазихимических
реакций образования единичных и кратных комплексов:
адсорбтив + свободная поверхность
[единичные комплексы],
адсорбтив + единичные комплексы <=> [двойные комплексы],
адсорбтив + двойные комплексы <=> [тройные комплексы] и т.д.
Слайд 40Уравнение БЭТ полимолекулярной адсорбции
Пусть θ1, θ2, θ3, θ4, … –
доля поверхности, занятая единичными, двойными, тройными и т.д. комплексами. Общая
величина адсорбции, а с учетом всех типов комплексов и их кратности, определяется как:
а = аm(θ1 + 2 θ2 + 3 θ3 + 4 θ4 + ...), (16)
где аm – емкость плотного монослоя. Выражения для констант равновесия соответствующих квазихимических реакций записываются в виде K1 = θ1/(Pθ0);
K2 = θ2/(Pθ1); K3 = θ3/(Рθ2) и т.д. (θ0 – доля свободной поверхности).
Слайд 41Уравнение БЭТ полимолекулярной адсорбции
Величина константы K1 обычно намного больше значений
K2, K3, K4, …, так как сила взаимодействия быстро убывает
по мере увеличения расстояния от поверхности.
Константы K2, K3, K4 и т.д. также не равны друг другу, однако разница между ними обычно намного меньше их отличия от K1.
Поэтому принимается допущение, что все эти константы, кроме K1, равны друг другу и близки константе равновесия на границе жидкость–пар, равной
KL = 1/Р0, где Р0 -давление насыщенных паров жидкой фазы адсорбтива при данной температуре.
Слайд 42Уравнение БЭТ полимолекулярной адсорбции
Это допущение позволяет переписать уравнения в виде
блока уравнений (17):
1= К1Р 0
2= К2Р 1= КL P 1=
1( Р/Р0)
3= К3Р 2= (КL P)2 = 1( Р/Р0)
4= К4Р 3= (КL P)3 = 1( Р/Р0 )
Слайд 43Уравнение БЭТ полимолекулярной адсорбции
Вводя эти уравнения в (16), получим
а =
аmК1Рϴ0 [ 1 + 2Р/Р0 + 3 ( Р/Р0)2 +....)
(18)
С другой стороны, баланс заполнения поверхности можно представить в виде :
ϴ0+ϴ1+ϴ2+ϴ3+ϴ4+...=ϴ0{1+K1P[1+P/P0+(P/P0)2 +...]}= 1.0
В этом уравнении выражение в квадратных скобках, где все значения Р/Р0 < 1, представляет убывающую геометрическую прогрессию
1+P/P0+(P/P0)2+(P/P0)3... = 1/(1-Р/Р0) (19)
Слайд 44Уравнение БЭТ полимолекулярной адсорбции
а = аmC (Р/Р0)/{[1-(Р/Р0)] [1+(C-1)(Р/Р0)]}
уравнение БЭТ.
Слайд 45Уравнение БЭТ полимолекулярной адсорбции
Это уравнение имеет две константы аm и
C, которые легко определяются из линейной формы уравнения БЭТ
Y=h/a(1-h)=1/( аmC)+(C-1)h/
аmC
( где h=Р/Р0) из наклона и отсекаемого на оси ординат отрезка соответствующего графика зависимости Y от h.
Слайд 46Уравнение БЭТ полимолекулярной адсорбции
Константа аm равна емкости заполненного монослоя, а
константа С, которую называют энергетической константой уравнения БЭТ и часто
обозначают как СБЭТ , согласно современной трактовке, равна :
СБЭТ =e S/R e (Q-L) /RT
где первая экспонента связана с изменениями энтропии при адсорбции,
а вторая - с так называемой чистой теплотой адсорбции, равной разнице изостерической теплоты адсорбции Q и теплоты конденсации чистого адсорбтива L в жидкость (т.е. скрытой теплоты испарения).
Слайд 47Уравнение БЭТ полимолекулярной адсорбции
При С>> 1 и малых значениях Р/Р0
уравнение БЭТ трансформируется в уравнение Ленгмюра.
Это уравнение широкое используется
для расчета емкости монослоя am, по которой далее рассчитывается площадь удельной поверхности катализаторов и адсорбентов. Если величина аm выражена в молях на г адсорбента, то удельная поверхность А с размерностью м2/г определяется по формуле
А = аm NA
где NA - число Авогадро, - площадка, приходящаяся на одну молекулу в заполненном монослое на поверхности адсорбента.
Слайд 48Уравнение БЭТ полимолекулярной адсорбции
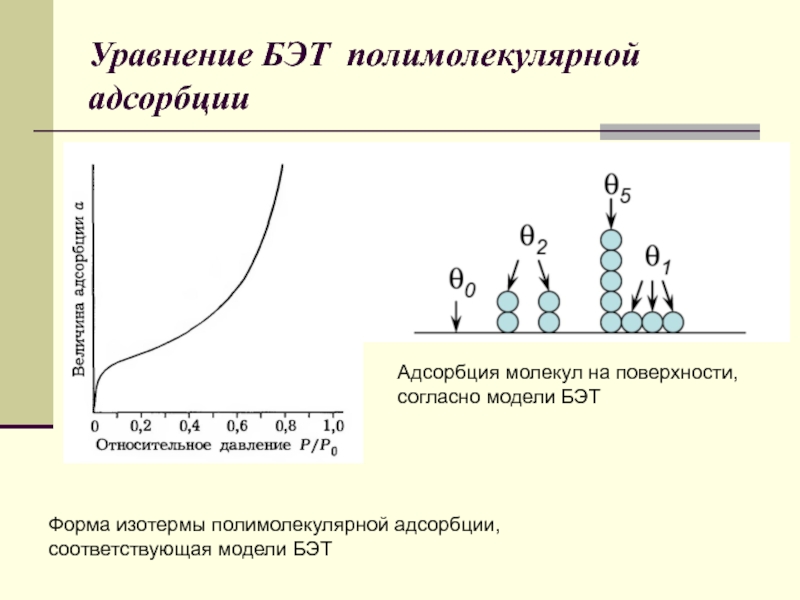
Форма изотермы полимолекулярной адсорбции,
соответствующая модели БЭТ
Адсорбция молекул на поверхности, согласно модели БЭТ
Слайд 49Уравнение БЭТ полимолекулярной адсорбции
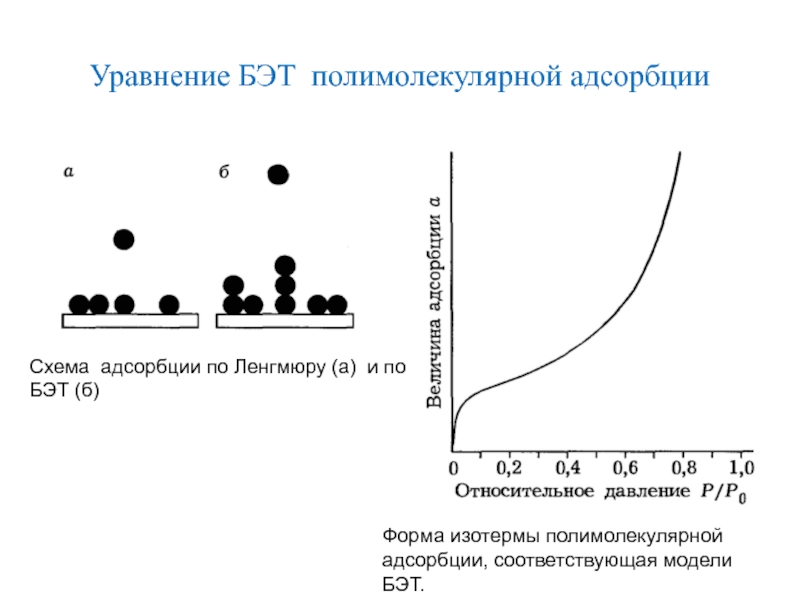
Схема адсорбции по Ленгмюру (а) и по
БЭТ (б)
Форма изотермы полимолекулярной адсорбции, соответствующая модели БЭТ.
Слайд 50Уравнение БЭТ полимолекулярной адсорбции
Модель БЭТ основывается на трёх важных допущениях:
1.
Считается, что поверхность адсорбента является однородной и, следовательно, все адсорбционные
центры энергетически эквивалентны.
2. Адсорбционные центры послойно заполняют молекулы адсорбата, причём молекулы во всех слоях, следующих за первым, рассматриваются как совершенно идентичные.
3. Модель учитывает лишь силы взаимодействия между молекулами адсорбата и адсорбента («вертикальные» силы) и пренебрегает силами взаимодействия между молекулами адсорбата на поверхности в данном адсорбционном слое («горизонтальные» силы).
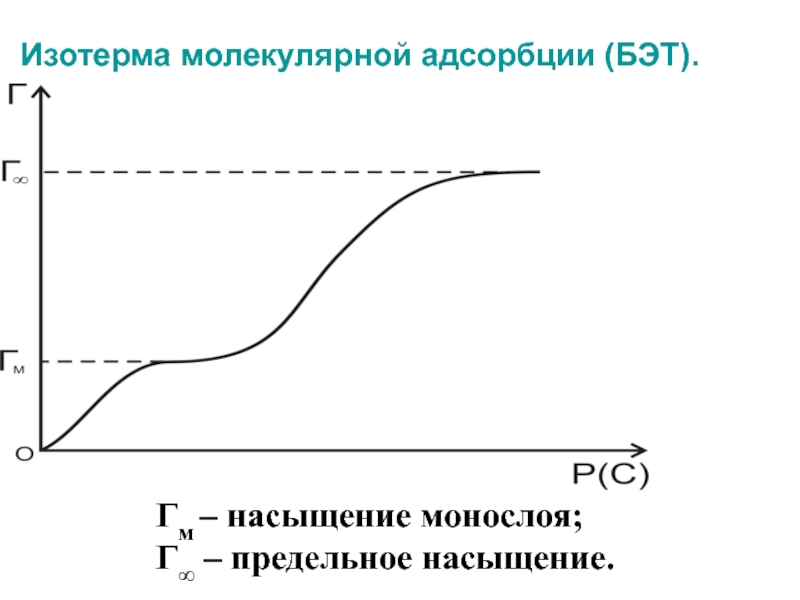
Слайд 51Изотерма молекулярной адсорбции (БЭТ).
Гм – насыщение монослоя;
Г∞ – предельное насыщение.
Слайд 52Уравнения изотерм адсорбции де Бура-Хилла и Фольмера.
Слайд 53Уравнения изотерм адсорбции де Бура-Хилла и Фольмера
Анализ численных значений К1Р0
и К2 показывает, что они могут изменяться, как правило, в
диапазоне 0 10, где поддиапазон 0 1 соответствуют очень слабым, а область значений 10 - очень сильным межмолекулярным взаимодействиям.
Слайд 54Уравнения изотерм адсорбции де Бура-Хилла и Фольмера
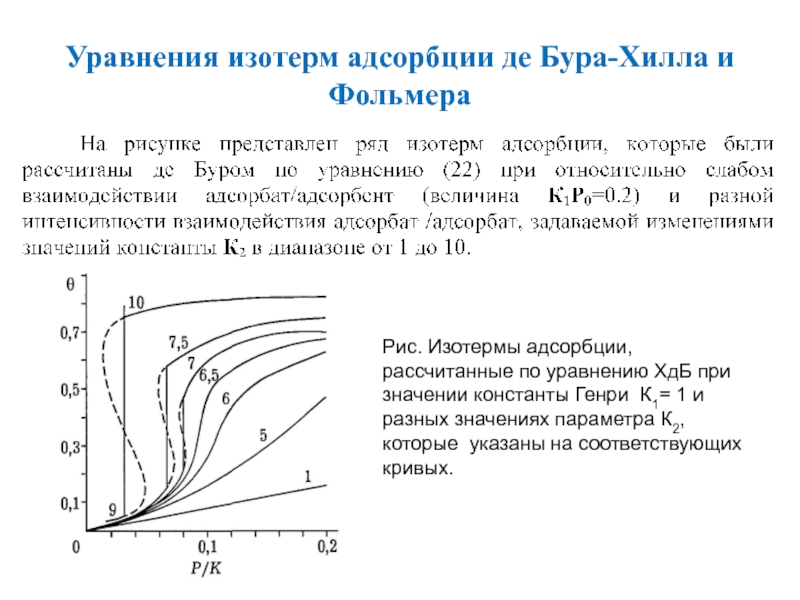
Рис. Изотермы адсорбции, рассчитанные
по уравнению ХдБ при значении константы Генри К1= 1 и
разных значениях параметра К2, которые указаны на соответствующих кривых.
Слайд 55Уравнения изотерм адсорбции де Бура-Хилла и Фольмера
Если исключить возможность пересыщений,
то, исходя из формы полученных кривых, следует ожидать скачкообразный рост
адсорбции при некоторых постоянных значениях давления.
Этот скачок соответствует двумерной конденсации сорбата, а область скачка - сосуществованию двух поверхностных фаз - “двумерного газа” и “двумерной жидкости”.
Аналогичные расчеты показывают, что увеличение значений К1Р0 смещает зоны двумерной конденсации вправо - в область более высоких давлений в газовой фазе.
Слайд 56Уравнения изотерм адсорбции де Бура-Хилла и Фольмера
Все рассмотренные изотермы рассчитаны
для адсорбции на идеально одно-родной поверхности, наиболее характерной для границы
жидкость/пар. Соответственно, полученные уравнения наиболее эффективны, например, для исследования адсорбции ПАВ на поверхности растворов, где действительно наблюдаются двумерные фазовые превращения газ/жидкость/твердоподобная пленка, и прояв-ляются дополнительные особенности, связанные с изменением ориентации адсор-бированных молекул относительно поверхности и т.д..
В случае твердых тел достаточно однородная поверхность может быть получена только в исключительных случаях - на графитизированных сажах, моно-кристаллах и т.д. При этом применение уравнения Хилла - де Бура дает разумные результаты.
Слайд 57ОСНОВНЫЕ ПОНЯТИЯ
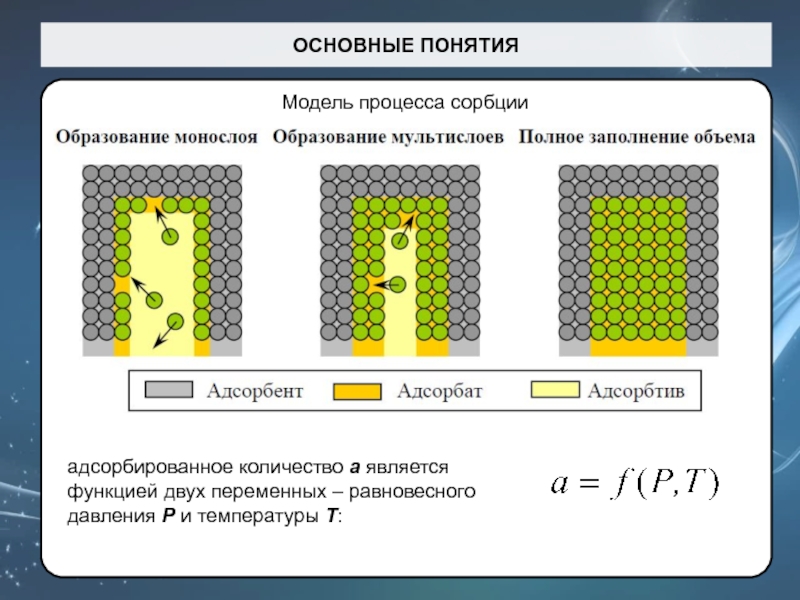
Модель процесса сорбции
адсорбированное количество a является функцией двух переменных
– равновесного давления P и температуры T:
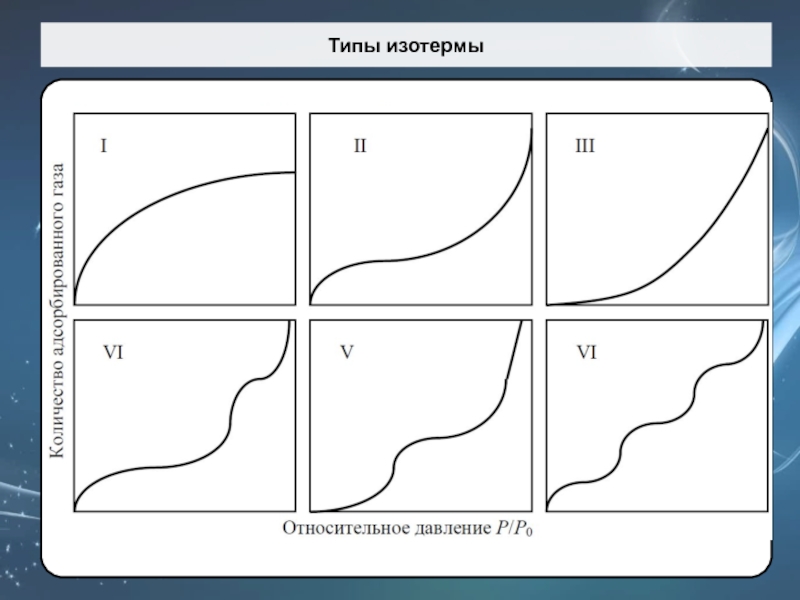
Слайд 59Типы изотермы
Первый типа (I) изотермы (изотерма Лангмюра) присущи, в основном,
микропористым образцам с относительно не большой поверхностью (активированный уголь или
цеолит).
Второй тип (II) отвечает полимолекулярной адсорбции. Такая изотерма присуща непористым или макропористым адсорбентам.
Слайд 60Типы изотермы
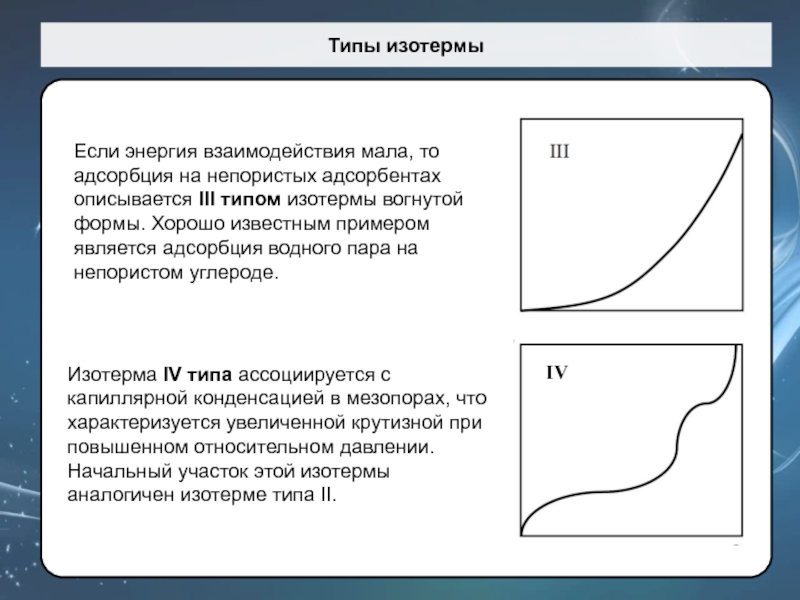
Если энергия взаимодействия мала, то адсорбция на непористых адсорбентах
описывается III типом изотермы вогнутой формы. Хорошо известным примером является
адсорбция водного пара на непористом углероде.
Изотерма IV типа ассоциируется с капиллярной конденсацией в мезопорах, что характеризуется увеличенной крутизной при повышенном относительном давлении. Начальный участок этой изотермы аналогичен изотерме типа II.
IV
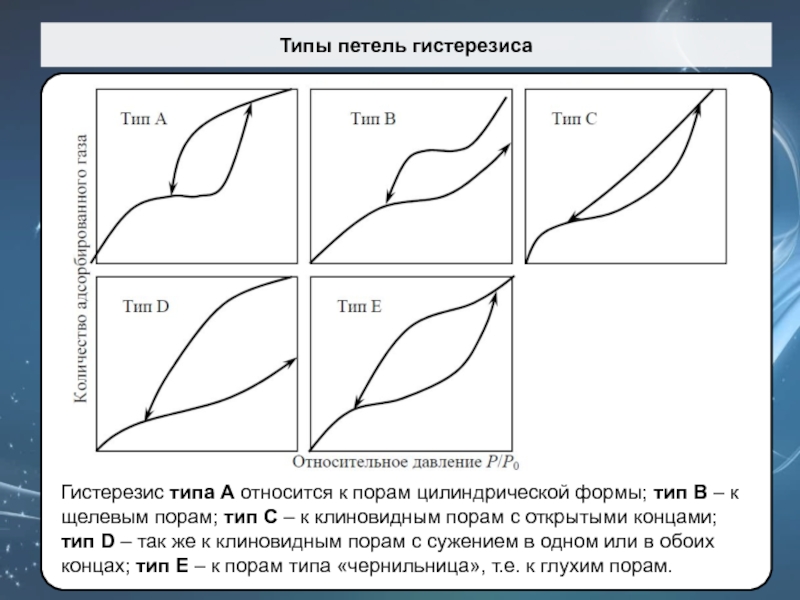
Слайд 61Типы петель гистерезиса
Гистерезис типа A относится к порам цилиндрической формы;
тип B – к щелевым порам; тип C – к
клиновидным порам с открытыми концами; тип D – так же к клиновидным порам с сужением в одном или в обоих концах; тип Е – к порам типа «чернильница», т.е. к глухим порам.
Слайд 62Определение удельной поверхности – модель БЭТ
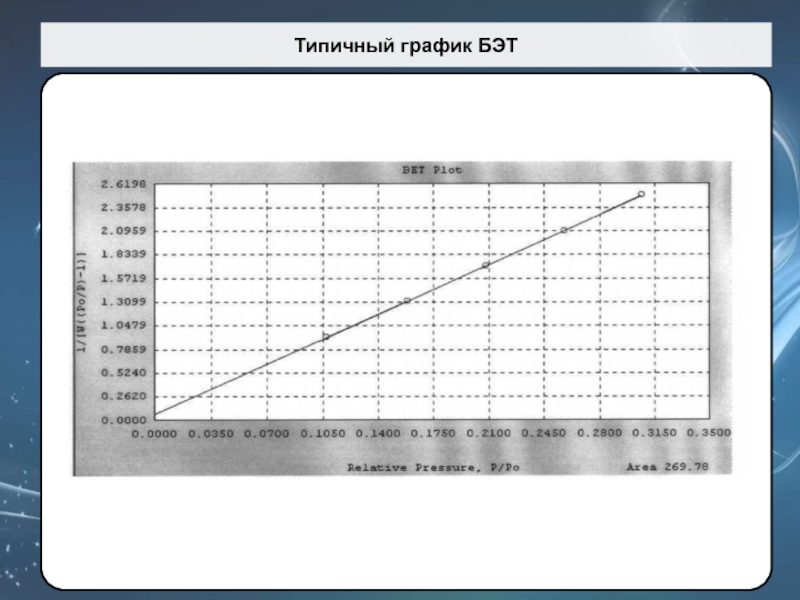
Уравнение БЭТ (Брунауэра-Эммета-Теллера):
где P –
давление газа, P0 – давление его насыщенных паров,
W -
масса газа, адсорбированного при относительном давлении Р/Р0, Wm – вес адсорбированного вещества, образующего покрывающий всю поверхность монослой, С – константа ВЕТ, относящаяся к энергии адсорбции в первом адсорбированном слое и, следовательно, ее значение характеризует взаимодействие адсорбент/адсорбат.
Удельную площадь поверхности S твердого вещества можно рассчитать из общей площади поверхности St и массы навески w по уравнению:
Acs=16,2 Å2
Слайд 64Определение пористости
Классификация пор по размера
Принципиальная схема адсорбции
на поверхности и в
объеме пор
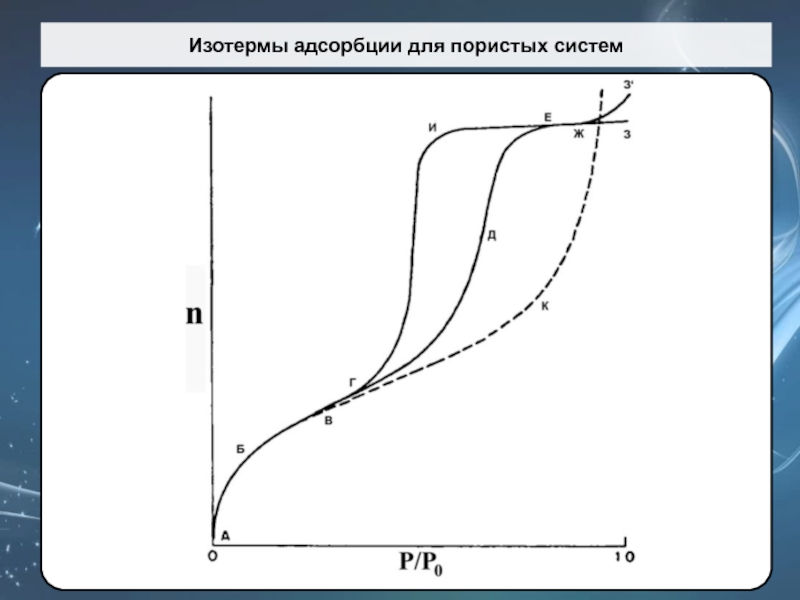
Слайд 65Изотермы адсорбции для пористых систем
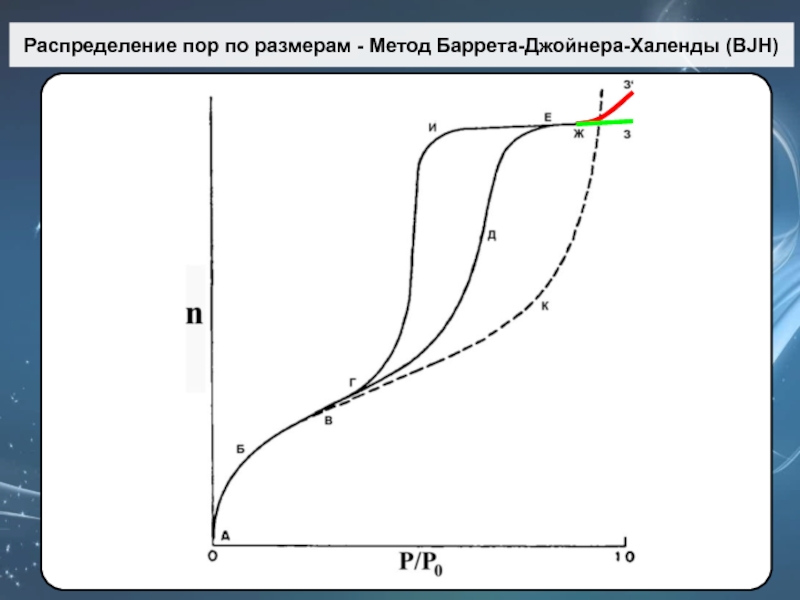
Слайд 66Распределение пор по размерам - Метод Баррета-Джойнера-Халенды (BJH)
Слайд 67Метод Баррета-Джойнера-Халенды (BJH)
где t – толщина адсорбированного слоя.
Метод Barrett-Joyner-Halenda (BJH),
предложенный в 1951 г. основан
на допущениях:
Поры имеют форму цилиндра
Истинный радиус пор
равен:
Радиус пор по Кельвину (rK) – это радиус при котором в порах происходит конденсация при относительном давлении Р/Р0.
t
rK
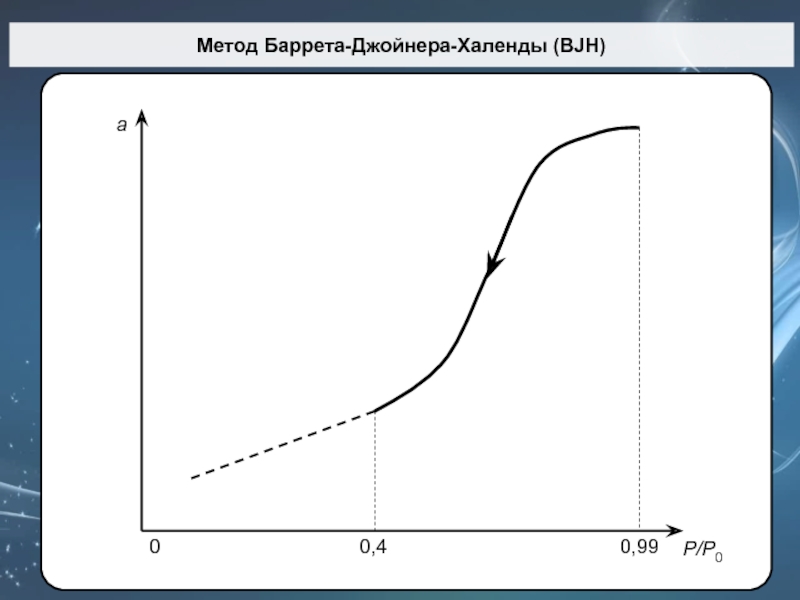
Слайд 68Метод Баррета-Джойнера-Халенды (BJH)
P/P0
0
Слайд 69NOVA 2200e Quantachrome
Точность измерений давления: 0,016 мм.рт.ст, 2*10-5 P0
Измеряемая площадь
поверхности (м2/г):
минимальная: 0,01
максимальная: >2,000
Диаметр пор: 3,5 - 2,000Å
Минимальный измеряемый объем
пор: 2,2*10-6 см3
Прибор позволяет получать следующие данные об образце:
• Изотермы адсорбции-десорбции
• Площадь поверхности: Одноточечный метод BET
• Площадь поверхности: Многоточечный метод BET
• Площадь микропор
• Объем микропор
• Распределение мезо- и макропор по размерам: Модель BJH
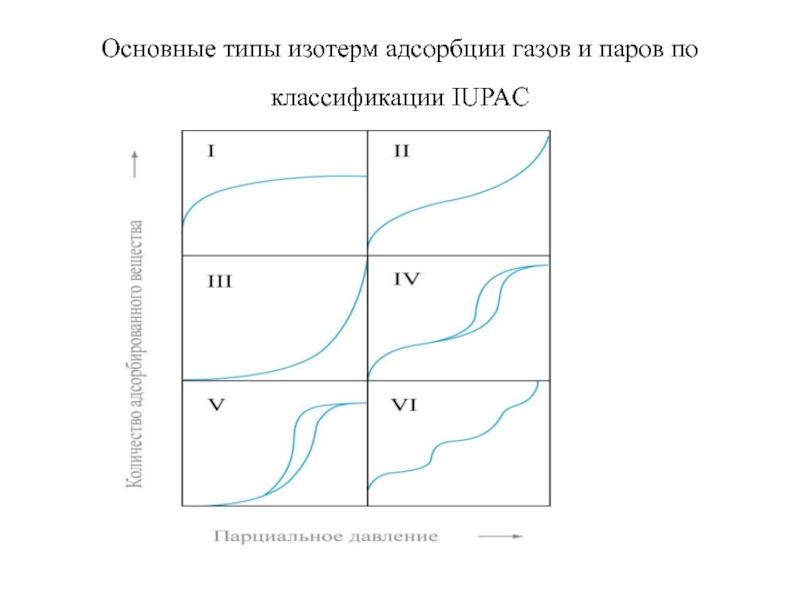
Слайд 71Основные типы изотерм адсорбции газов и паров по классификации IUPAC
Слайд 72Основные типы изотерм адсорбции газов и паров по классификации IUPAC
I-Vтипы
соответствуют классификации Брунауэра (1940 г)
VI-характерен для адсорбции инертных газов при
77К на однородной поверхности графитированных саж или монокристаллов; ступеньки соответствуют последователь-ному заполнению отдельных монослоев.
В области малых давлений все ИА имеют участки, где выполняется уравнение Генри; наклон этих участков определяется взаимодействием адсорбат-адсорбент.
Изотермы I типа – характерны для физической адсорбции в микропористых системах ; а также для хемосорбции, соответствующей мономолекулярной адсорбции.
Слайд 73Основные типы изотерм адсорбции газов и паров по классификации IUPAC
Изотермы
II -типа – характерны для непористых или макропористых адсорбентов с
сильным взаимодействием адсорбат-адсорбент (Г-Х), о чем свидетельствует выпуклый начальный участок ИА.
Ослабление такого взаимодействия приводит к ИА III –типа, характерны для непористых носителей.
ИА III –типа сравнительно редко встречающийся тип изотерм образования полислоя из газовой среды на твердом адсорбенте, для тел, потенциал монослоя которых мал и имеет тот же порядок, что и теплота конденсации адсорбтива. Изотермы III типа характерны для случая слабого взаимодействия газа с адсорбентом при адсорбции на непористых твердых телах.
Слайд 74Основные типы изотерм адсорбции газов и паров по классификации IUPAC
ИА
IV иV-типов –характерны для адсорбции на пористом твердом теле, отличаются
тем, что для них характерна конечная адсорбция при приближении давления пара к давлению насыщенного пара Рs; имеют петлю капиллярного конденсационного гистерезиса, что указывает на наличие мезопор (2-100 нм)
Слайд 75Основные типы изотерм адсорбции газов и паров по классификации IUPAC
Изотермы
IV и V типов характерны для адсорбции в высокопористых телах,
причем изотерма V типа отвечает случаю слабого взаимодействия газ/адсорбент.
А наличие петель на этих изотермах связано с капиллярной конденсацией.
Слайд 76Основные положения теории Поляни
Адсорбция обусловлена чисто физическими силами (силами Ван-дер-Ваальса).
Основной вклад вносят дальнодействующие дисперсионные силы аддитивные и не зависящие
от температуры.
На поверхности адсорбента нет активных центров (энергетически однородная поверхность).
Слайд 77Основные положения теории Поляни
Адсорбция обусловлена чисто физическими силами (силами Ван-дер-Ваальса).
Основной вклад вносят дальнодействующие дисперсионные силы аддитивные и не зависящие
от температуры.
На поверхности адсорбента нет активных центров (энергетически однородная поверхность).
Слайд 78Основные положения теории Поляни
Адсорбционные силы действуют на больших расстояниях, что
приводит к образованию полимолекулярного слоя. По мере удаления от поверхности
действие адсорбционных сил уменьшается и на некотором расстоянии становится практически равным нулю.
Адсорбционные силы не зависят от температуры.
Практически все адсорбированное вещество находится на поверхности адсорбента в жидком состоянии.
Слайд 79Основные положения теории Поляни
Характеристическая кривая не зависит от температуры и
индивидуальна и характерна для каждого вида адсорбента для сходных адсорбатов.
Адсорбционные потенциалы для разных адсорбатов на одном и том же адсорбенте находятся в постоянном соотношении.
Это соотношение называется коэффициентом афинности ( близости, сродства) :
β = ε1/ ε2
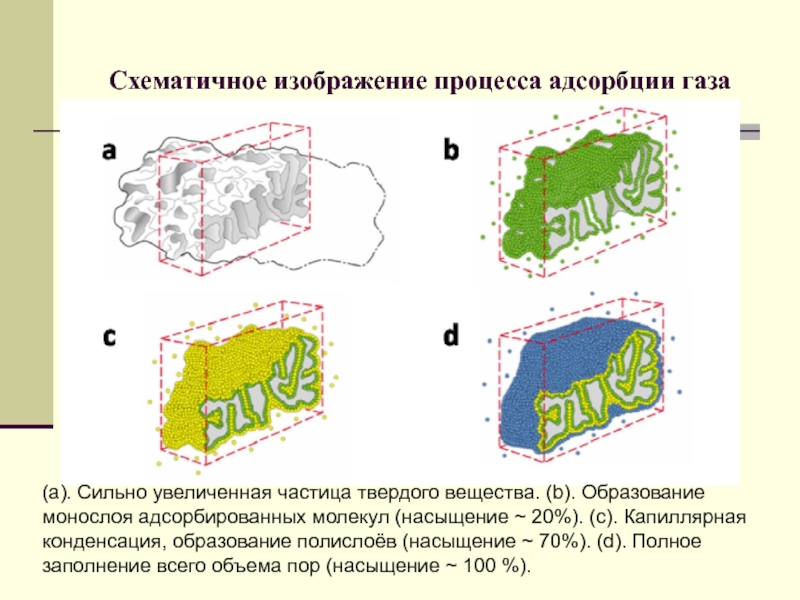
Слайд 80Схематичное изображение процесса адсорбции газа
(а). Сильно увеличенная частица твердого
вещества. (b). Образование монослоя адсорбированных молекул (насыщение ~ 20%). (c).
Капиллярная конденсация, образование полислоёв (насыщение ~ 70%). (d). Полное заполнение всего объема пор (насыщение ~ 100 %).
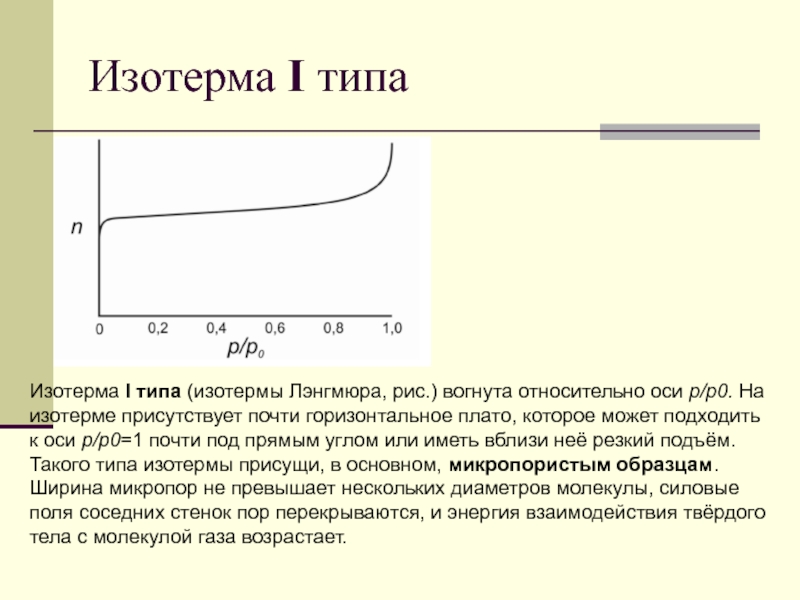
Слайд 81Изотерма I типа
Изотерма I типа (изотермы Лэнгмюра, рис.) вогнута
относительно оси р/р0. На изотерме присутствует почти горизонтальное плато, которое
может подходить к оси р/р0=1 почти под прямым углом или иметь вблизи неё резкий подъём. Такого типа изотермы присущи, в основном, микропористым образцам. Ширина микропор не превышает нескольких диаметров молекулы, силовые поля соседних стенок пор перекрываются, и энергия взаимодействия твёрдого тела с молекулой газа возрастает.
Слайд 82Изотерма I типа
Это вызывает отклонение изотермы, особенно в области малых
относительных давлений, в
область больших величин адсорбции.
Подобного рода взаимодействия достаточно
сильны, чтобы полное заполнение пор происходило при очень низком относительном давлении.
Изотермы этого типа описывают адсорбцию на углеродных адсорбентах, цеолитах, силикагелях.
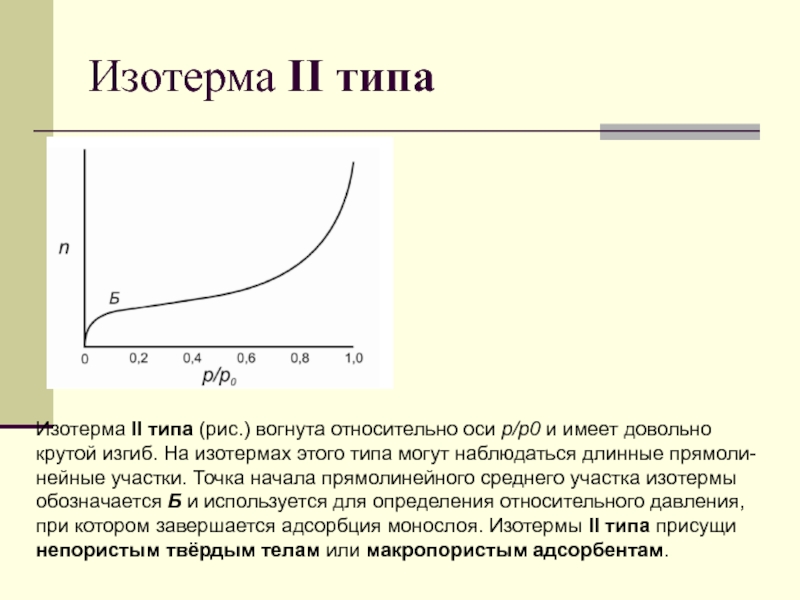
Слайд 83Изотерма II типа
Изотерма II типа (рис.) вогнута относительно оси
р/р0 и имеет довольно крутой изгиб. На изотермах этого типа
могут наблюдаться длинные прямоли-нейные участки. Точка начала прямолинейного среднего участка изотермы обозначается Б и используется для определения относительного давления, при котором завершается адсорбция монослоя. Изотермы II типа присущи непористым твёрдым телам или макропористым адсорбентам.
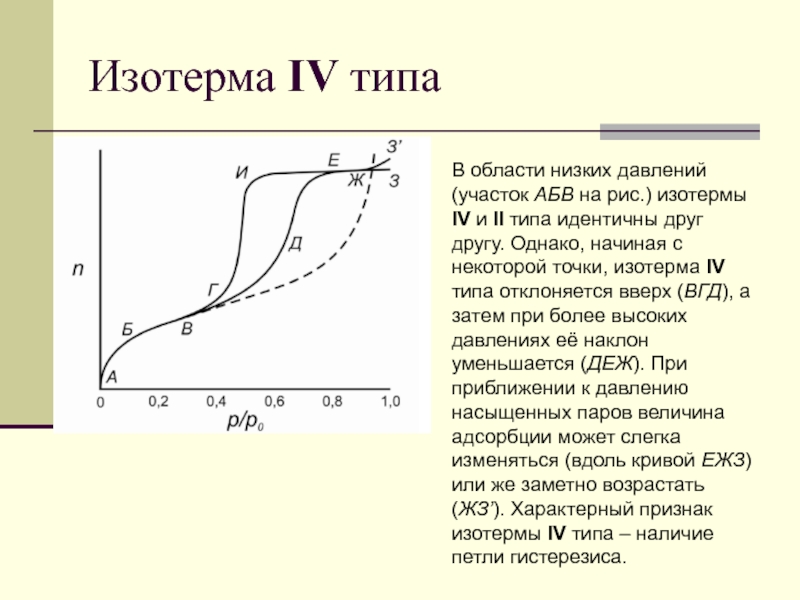
Слайд 84Изотерма IV типа
В области низких давлений (участок АБВ на
рис.) изотермы IV и II типа идентичны друг другу. Однако,
начиная с некоторой точки, изотерма IV типа отклоняется вверх (ВГД), а затем при более высоких давлениях её наклон уменьшается (ДЕЖ). При приближении к давлению насыщенных паров величина адсорбции может слегка
изменяться (вдоль кривой ЕЖЗ) или же заметно возрастать (ЖЗ’). Характерный признак
изотермы IV типа – наличие петли гистерезиса.
Слайд 85Изотерма IV типа
Форма петли может быть различной для разных адсорбционных
систем;
однако, как видно из рис., величина адсорбции при любом
данном относительном давлении для десорбционной ветви (ЕИГ) всегда больше, чем для адсорбционной (ГДЕ).
Петля является воспроизводимой, если десорбция начинается с точки, расположенной выше точки Е, которая представляет собой верхнюю точку петли.
IV тип изотерм адсорбции характерен для мезопористых твёрдых тел
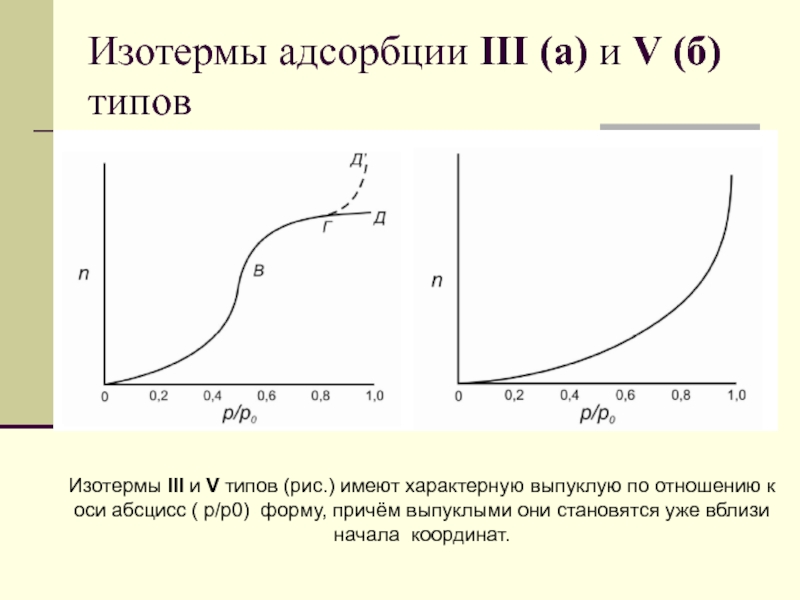
Слайд 86Изотермы адсорбции III (а) и V (б) типов
Изотермы III и
V типов (рис.) имеют характерную выпуклую по отношению к оси
абсцисс ( р/р0) форму, причём выпуклыми они становятся уже вблизи начала координат.
Слайд 87Изотермы адсорбции III (а) и V (б) типов
Изотерма III типа
остаётся выпуклой на всём своём протяжении, в то время как
на изотерме V типа при довольно высоких относительных давлениях (часто при р/р0 ≥ 0.5) имеется точка перегиба, так что изотерма изгибается и в области полимолекулярной адсорбции принимает форму плато (ГД на рис. б).
Иногда при давлении, близкому к давлению насыщенных паров, наблюдается подъём изотермы (ГД’ на рис. б) приписываемый адсорбции в крупных мезопорах и макропорах.
Слайд 88Изотермы адсорбции III (а) и V (б) типов
Изотермы адсорбции III
и V типов характерны для систем, в которых дисперсионное взаимодействие
газ – твёрдое тело меньше взаимодействия молекул адсорбата друг с другом.
Из-за слабого взаимодействия адсорбент – адсорбат поглощение газа при низких давлениях мало; однако, как скоро молекула оказывается адсорбированной, силы взаимодействия адсорбат – адсорбат промотируют дальнейшую адсорбцию, то есть процесс имеет кооперативный характер, и изотерма становится выпуклой по отношению к оси давлений.
Слайд 89Изотермы адсорбции III (а) и V (б) типов
Изотермы III типа
наблюдаются при адсорбции на непористых и макропористых твёрдых телах,
а
изотермы V типа – при адсорбции на мезопо-ристых и микропористых.
Экспериментально изотермы III типа получены для адсорбции паров воды и алканов на неполярных твёрдых телах (например, углеродных адсорбентах, органических высокомолекулярных полимерах: полиэтилен, полиметилметакрилат).















![Процессы на поверхности раздела твердое тело -газ Другие уравнения мономолекулярной локализованной адсорбции Уравнение Фаулера-Гугенгейма:Р = [ϴ/K(1-ϴ)] exp[-K1ϴ/RT] (11)где Другие уравнения мономолекулярной локализованной адсорбции Уравнение Фаулера-Гугенгейма:Р = [ϴ/K(1-ϴ)] exp[-K1ϴ/RT] (11)где первый член в квадратных скобках -](/img/thumbs/df1988ff20470036f4a1cae1580e91b2-800x.jpg)










![Процессы на поверхности раздела твердое тело -газ Уравнение БЭТ полимолекулярной адсорбцииа = аmC (Р/Р0)/{[1-(Р/Р0)] [1+(C-1)(Р/Р0)]} уравнение БЭТ. Уравнение БЭТ полимолекулярной адсорбцииа = аmC (Р/Р0)/{[1-(Р/Р0)] [1+(C-1)(Р/Р0)]} уравнение БЭТ.](/img/thumbs/22ec236cab2e41e155e87683fdca9ccb-800x.jpg)