Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Проверка домашнего задания
Содержание
- 1. Проверка домашнего задания
- 2. Ответьте на вопросы:1. Объясните, какая фигура называется
- 3. № 88Начертите треугольник DEF так, чтобы угол
- 4. № 90Сторона AB треугольника ABC равна 17
- 5. № 91Периметр треугольника равен 48 см, а
- 6. Диктант
- 7. Вариант 1. Задание 1DEKНазовите углы ΔDEK прилежащие к стороне ЕК
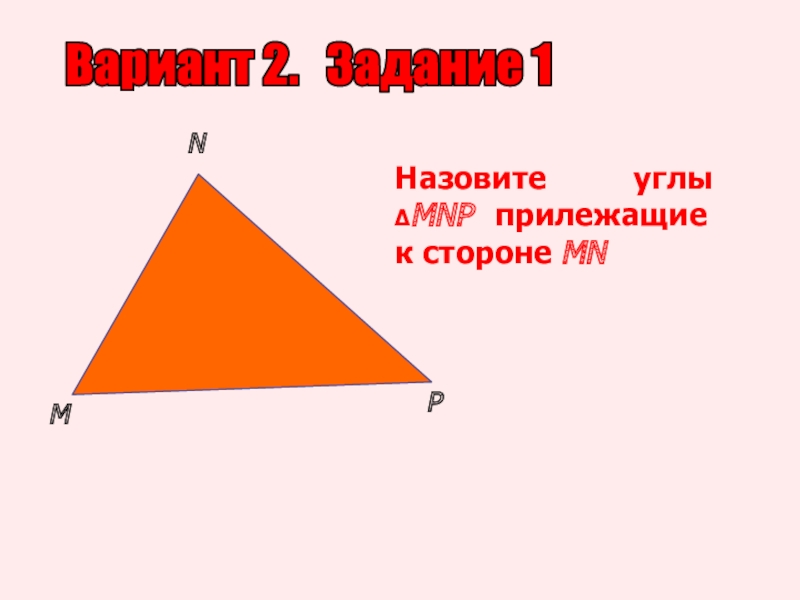
- 8. Вариант 2. Задание 1МNPНазовите углы ΔMNP прилежащие к стороне MN
- 9. Вариант 1. Задание 2DEKНазовите угол ΔDEK, заключен- ный между сторо- нами DE иDК
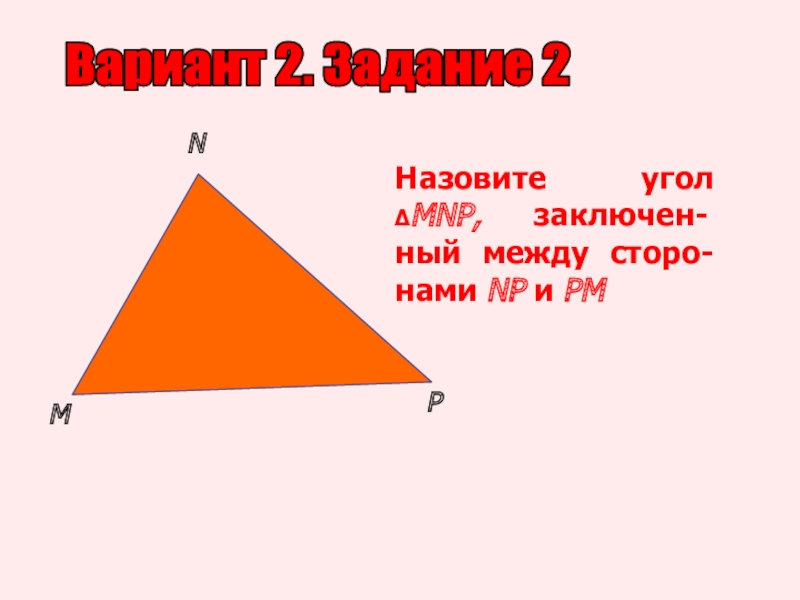
- 10. Вариант 2. Задание 2MNPНазовите угол ΔMNP, заключен- ный между сторо- нами NP и PM
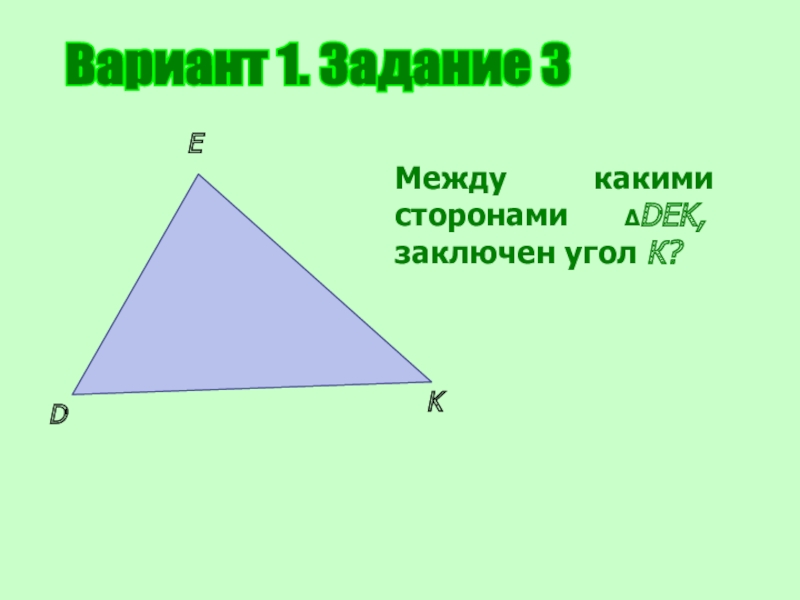
- 11. Вариант 1. Задание 3DEKМежду какими сторонами ΔDEK, заключен угол К?
- 12. Вариант 2. Задание 3MNPМежду какими сторонами ΔMNP, заключен угол N?
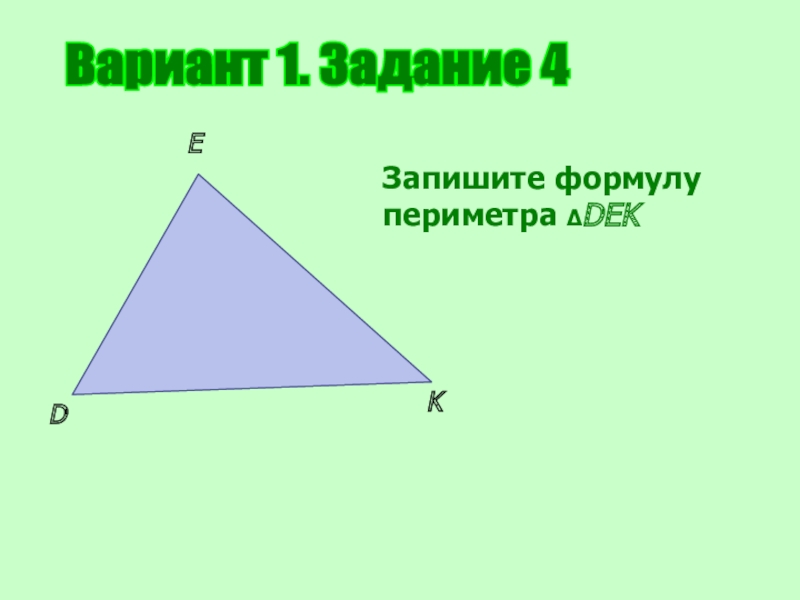
- 13. Вариант 1. Задание 4DEKЗапишите формулу периметра ΔDEK
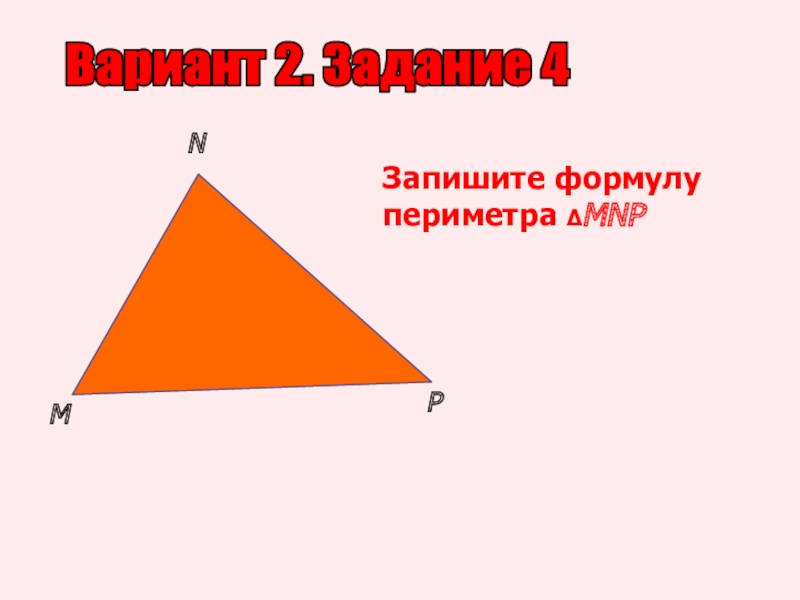
- 14. Вариант 2. Задание 4MNPЗапишите формулу периметра ΔMNP
- 15. Вариант 1. Задание 5 ΔАВС = ΔPSK. Назовите равные стороны и равные углы в этих треугольниках
- 16. Вариант 2. Задание 5 ΔFNB = ΔXYZ. Назовите равные стороны и равные углы в этих треугольниках
- 17. К л а с с н а
- 18. I признак равенства треугольников
- 19. Треугольники АВС и А1В1С1 совместятся, значит, они
- 20. К17см23смДля красного треугольника найдите равный и щёлкните по нему мышкой.23см23см23см17см17см17см37540540Проверка540Неверно!САОМВNXODEQ
- 21. ПроверкаОАВКМ Ученик утверждает, что АОВ= МОК по I признаку равенства треугольников.Согласны ли вы? 12
- 22. Проверка (2)AДоказать: AOD = SOFOFSD№ 1
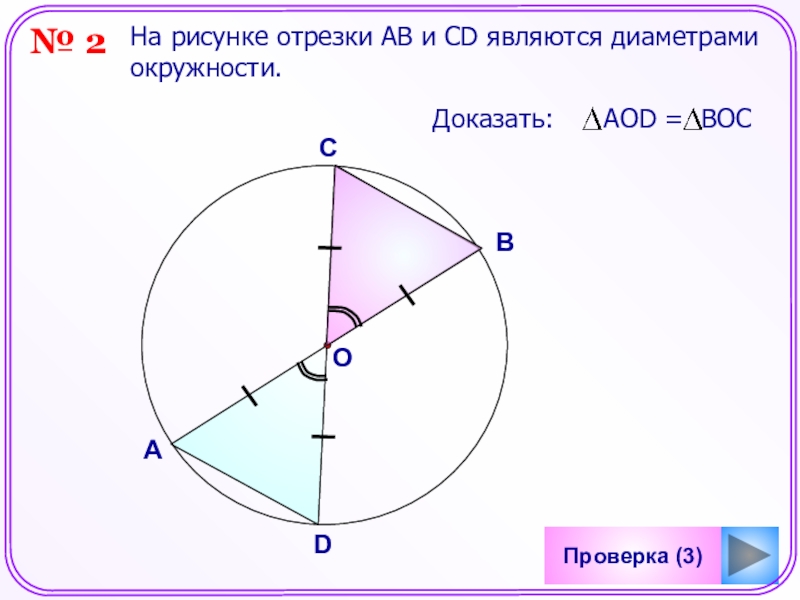
- 23. Проверка (3)На рисунке отрезки АB и СD являются диаметрами окружности. АВDCO№ 2
- 24. Проверка (2)AДоказать: АВК = СBКВКС№ 3
- 25. СПроверка (2)BАОВM – биссектриса угла АВО. Доказать:
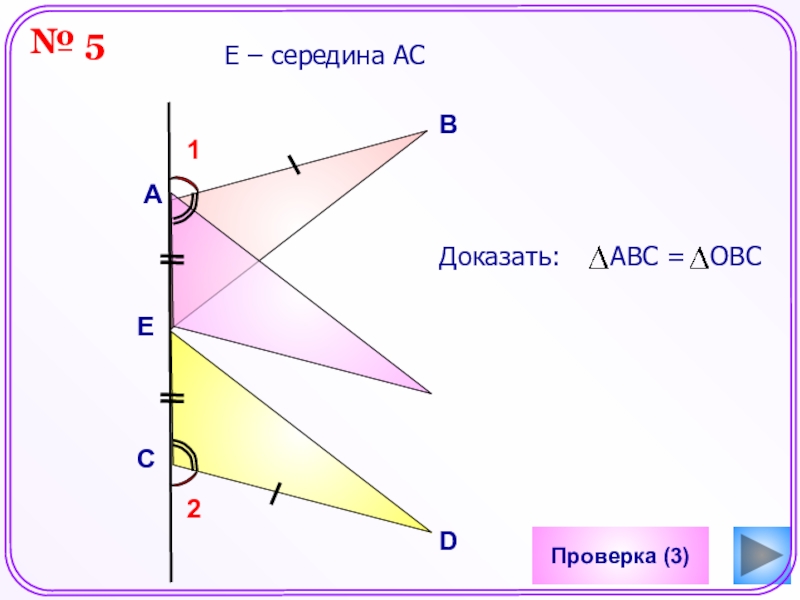
- 26. Проверка (3)ЕЕ – середина АС АВDC12№ 5
- 27. Домашнее заданиеп.15, вопросы 3 – 4 (устно, стр. 49);Решить задачи № 94; 95.
- 28. Скачать презентанцию
Слайды и текст этой презентации
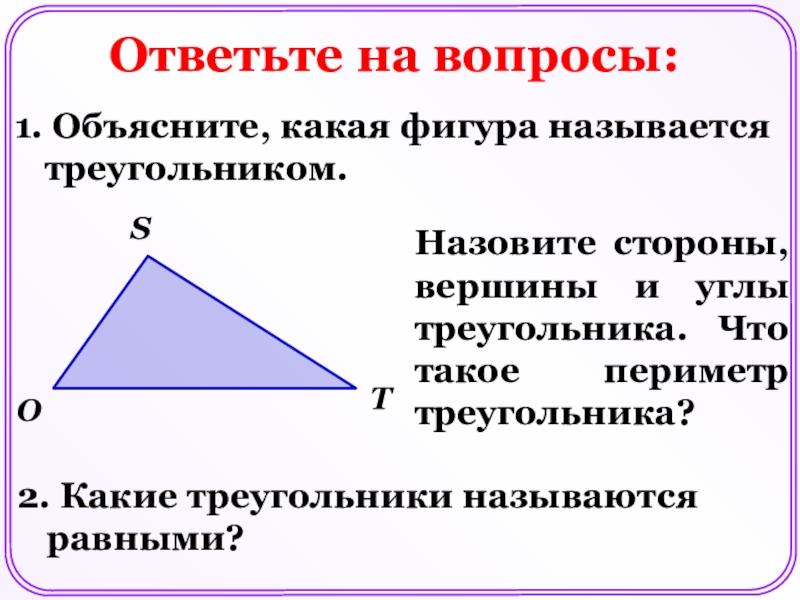
Слайд 2Ответьте на вопросы:
1. Объясните, какая фигура называется треугольником.
Назовите стороны, вершины
и углы треугольника. Что такое периметр треугольника?
равными?Слайд 3№ 88
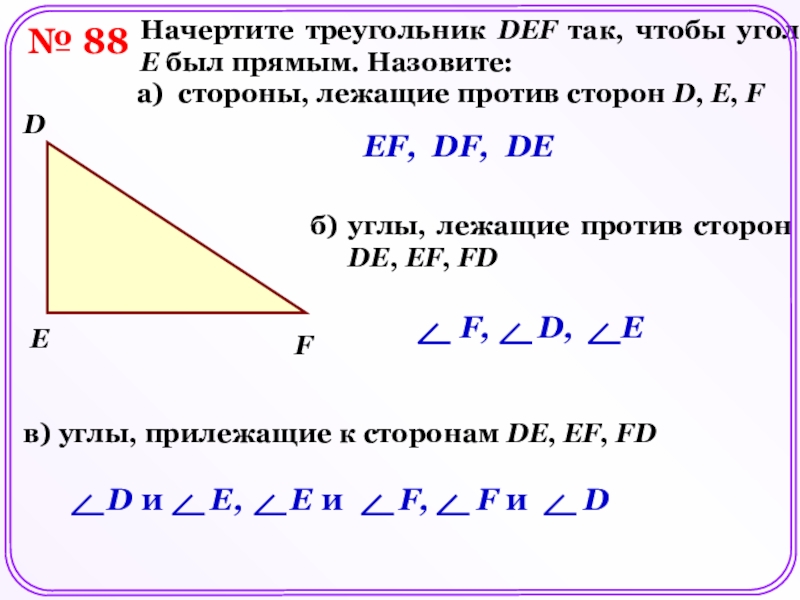
Начертите треугольник DEF так, чтобы угол E был прямым.
Назовите:
F
D
E
а) стороны, лежащие против сторон D, E, F
EF, DF,
DEб) углы, лежащие против сторон DE, EF, FD
в) углы, прилежащие к сторонам DE, EF, FD
Слайд 4№ 90
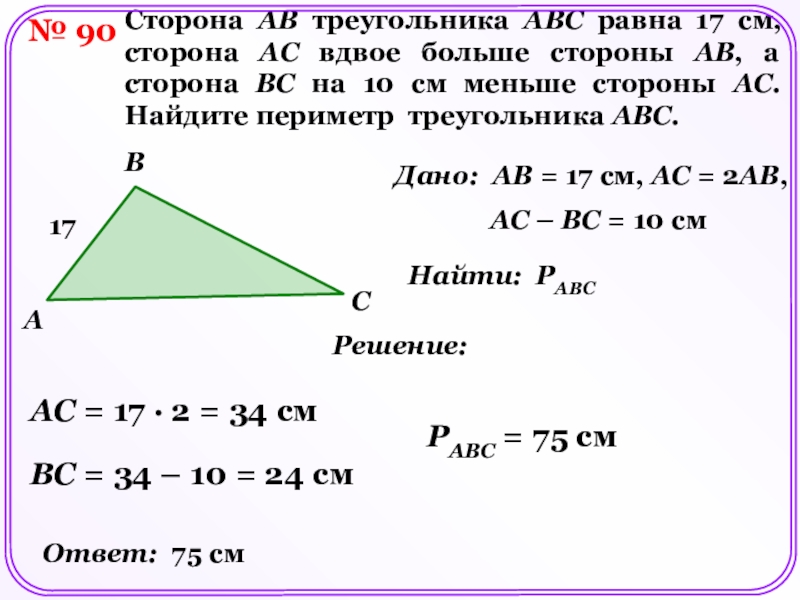
Сторона AB треугольника ABC равна 17 см, сторона AC
вдвое больше стороны AB, а сторона BC на 10 см
меньше стороны AC. Найдите периметр треугольника ABC.Дано: AB = 17 см, AC = 2AB,
AC – BC = 10 см
Найти: PABC
Решение:
Ответ: 75 см
C
A
B
AC = 17 · 2 = 34 см
BC = 34 – 10 = 24 см
PABC = 75 см
17
Слайд 5№ 91
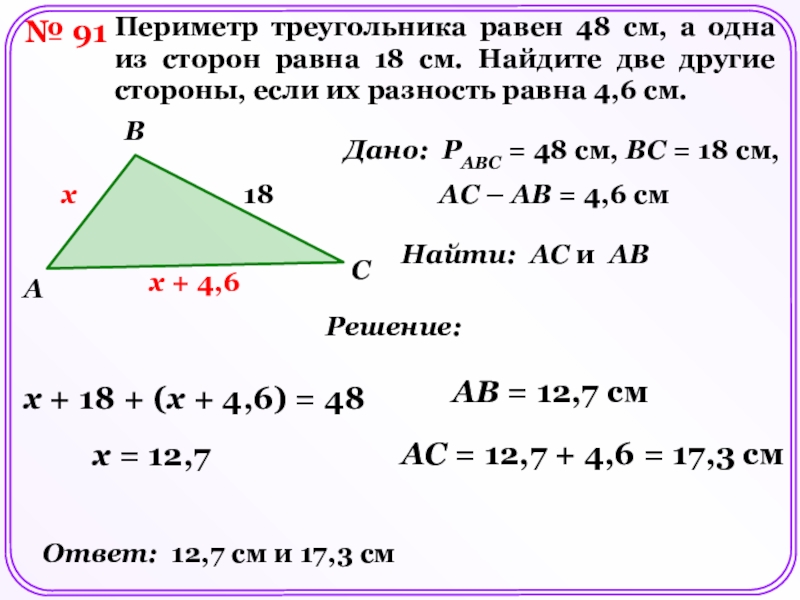
Периметр треугольника равен 48 см, а одна из сторон
равна 18 см. Найдите две другие стороны, если их разность
равна 4,6 см.Дано: PABC = 48 см, BC = 18 см,
AC – AB = 4,6 см
Найти: AC и AB
Решение:
Ответ: 12,7 см и 17,3 см
C
A
B
x + 18 + (x + 4,6) = 48
x
18
x + 4,6
x = 12,7
AB = 12,7 см
AC = 12,7 + 4,6 = 17,3 см
Слайд 15Вариант 1. Задание 5
ΔАВС = ΔPSK. Назовите равные стороны
и равные углы в этих треугольниках
Слайд 16Вариант 2. Задание 5
ΔFNB = ΔXYZ. Назовите равные стороны
и равные углы в этих треугольниках
Слайд 18I признак равенства треугольников
по двум сторонам
и углу между ними.Если две стороны и угол между ними одного треугольника соответственно равны двум
сторонам и углу между ними другого треугольника,
то такие треугольники равны.
У
С
Л
О
В
И
Е
З А К Л Ю Ч Е Н И Е
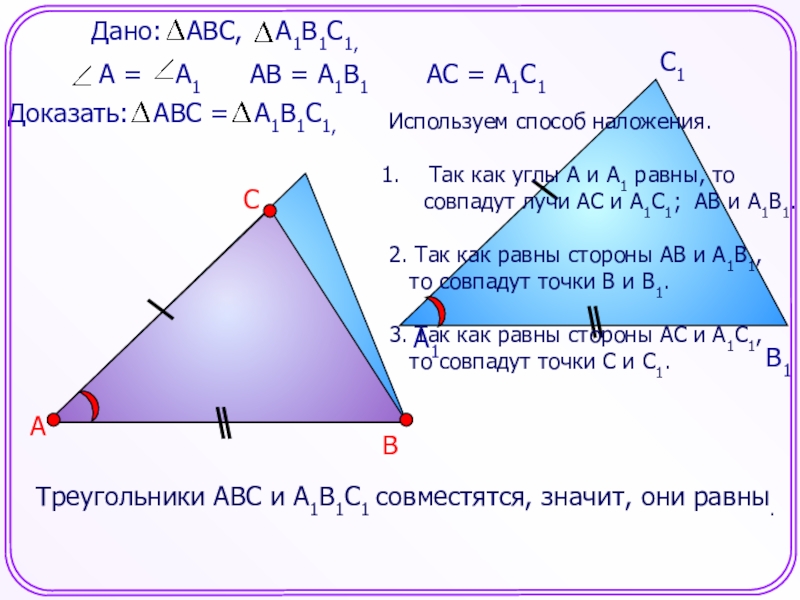
Слайд 19Треугольники АВС и А1В1С1 совместятся, значит, они равны.
А
В
С
А1
В1
С1
АВ = А1В1
АС
= А1С1
Используем способ наложения.
Так как углы А и А1 равны,
то совпадут лучи АС и А1С1; АВ и А1В1.
2. Так как равны стороны АВ и А1В1,
то совпадут точки В и В1.
3. Так как равны стороны АС и А1С1,
то совпадут точки С и С1.
Слайд 20К
17см
23см
Для красного треугольника найдите равный
и щёлкните по нему мышкой.
23см
23см
23см
17см
17см
17см
37
540
540
Проверка
540
Неверно!
С
А
О
М
В
N
X
O
D
E
Q
Слайд 21Проверка
О
А
В
К
М
Ученик утверждает, что
АОВ= МОК по I признаку
равенства треугольников.
Согласны ли вы?
1
2
Слайд 25С
Проверка (2)
B
А
О
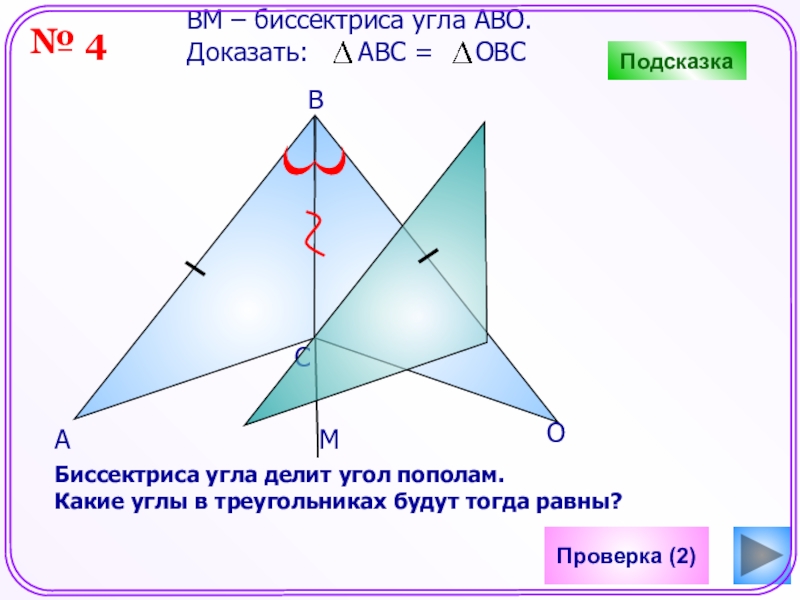
ВM – биссектриса угла АВО.
Доказать: АВС
= ОВС
Подсказка
Биссектриса угла делит угол пополам.
Какие углы в
треугольниках будут тогда равны?М
№ 4