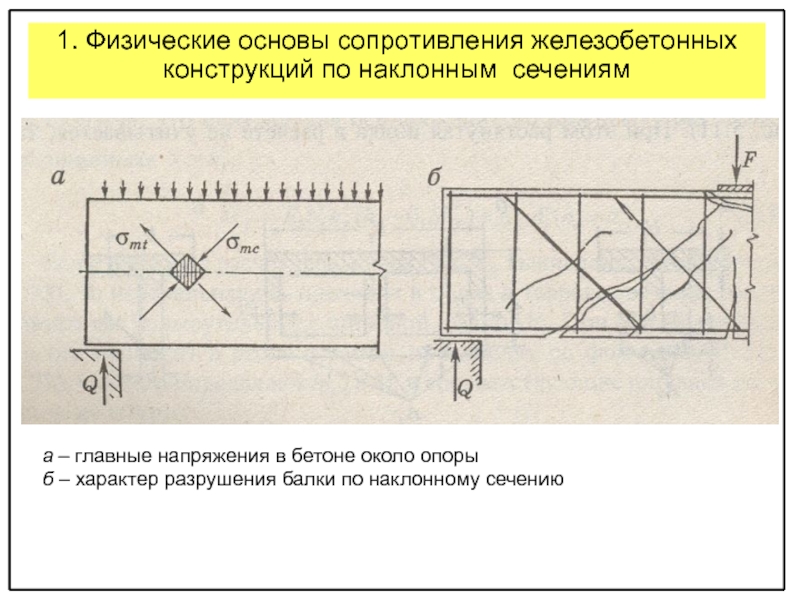
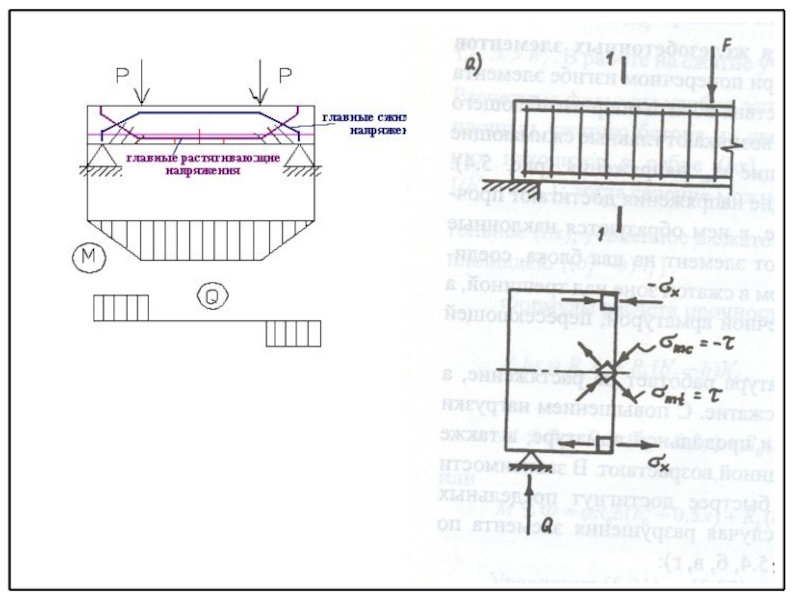
Расчет элементов по наклонным сечениям

Содержание

1. Расчет элементов по наклонным сечениям
2. Вопросы:Физические основы сопротивления железобетонных конструкций по наклонным
3. 1. Физические основы сопротивления железобетонных конструкций по
4. Слайд 4
5. Случай 13 случая разрушения изгибаемых элементов по
6. 1 - критическая наклонная трещина; 2 -
7. 2. Расчет на действие поперечной силы по
8. 3. Прочность железобетонного элемента по наклонной трещине
9. Распределение усилий в наклонном сечении изгибаемой конструкцииУсловие прочности (2)
10. Коэффициент ϕb2, =1,5Поперечную силу Qb определяют по формуле но принимают не более и не менее ;
11. где φsw – коэффициент, принимаемый равным 0,75;qsw –
12. Поперечную арматуру учитывают в расчете, если соблюдается
13. Слайд 13
14. Слайд 14
15. Слайд 15
16. Слайд 16
17. Слайд 17
18. Скачать презентанцию

Вопросы:Физические основы сопротивления железобетонных конструкций по наклонным сечениямРасчет на действие поперечной силы по наклонной полосе между наклонными трещинами Прочность железобетонного элемента по наклонной трещине на действие поперечной силы Условия прочности наклонных

Главная
Разное
Расчет элементов по наклонным сечениям

Слайды и текст этой презентации

Слайд 1Томский государственный архитектурно-строительный университет
Кафедра
«Железобетонные и каменные конструкции»
Лекция 10.
Расчет

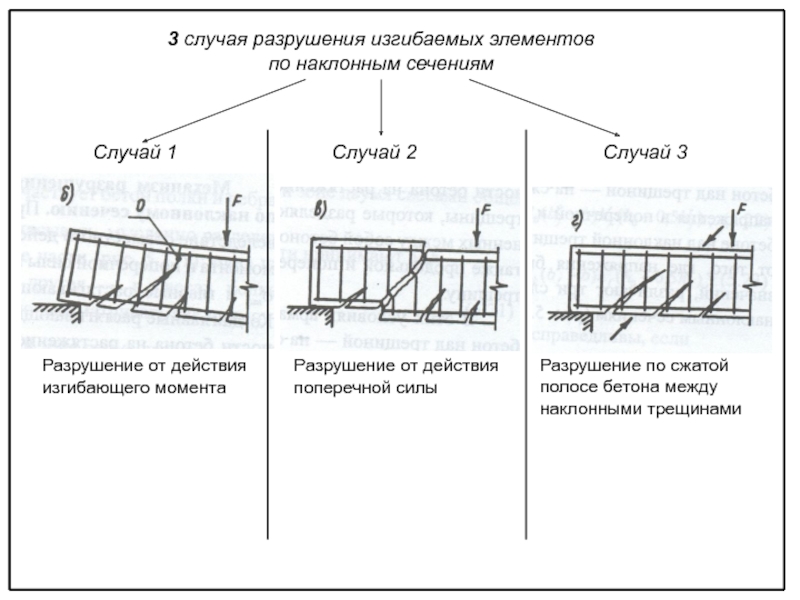
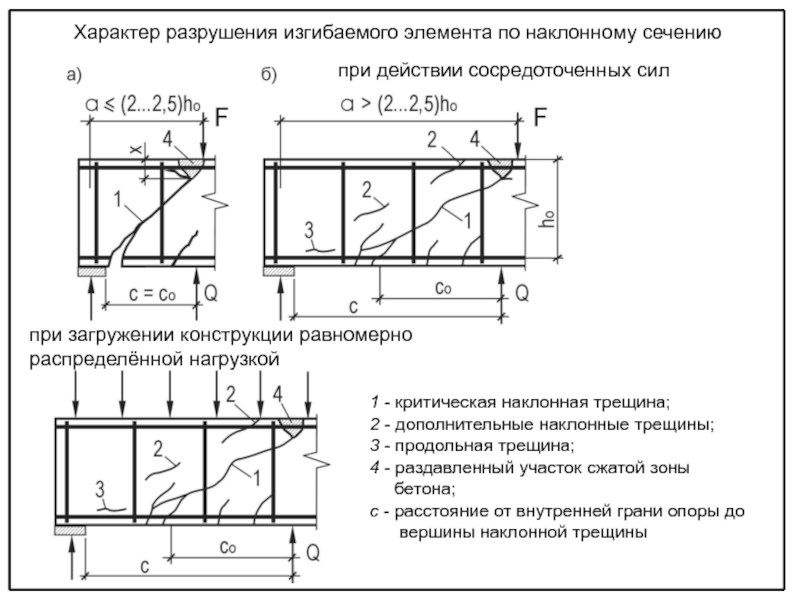
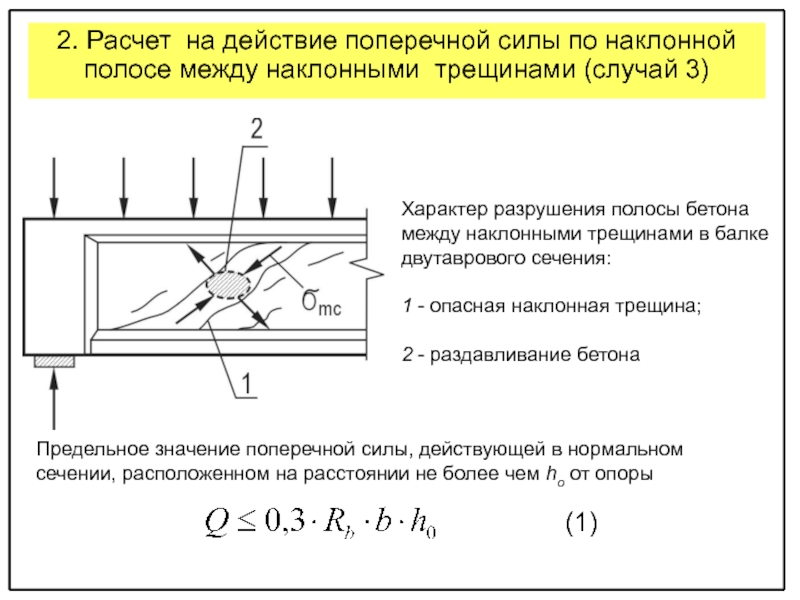
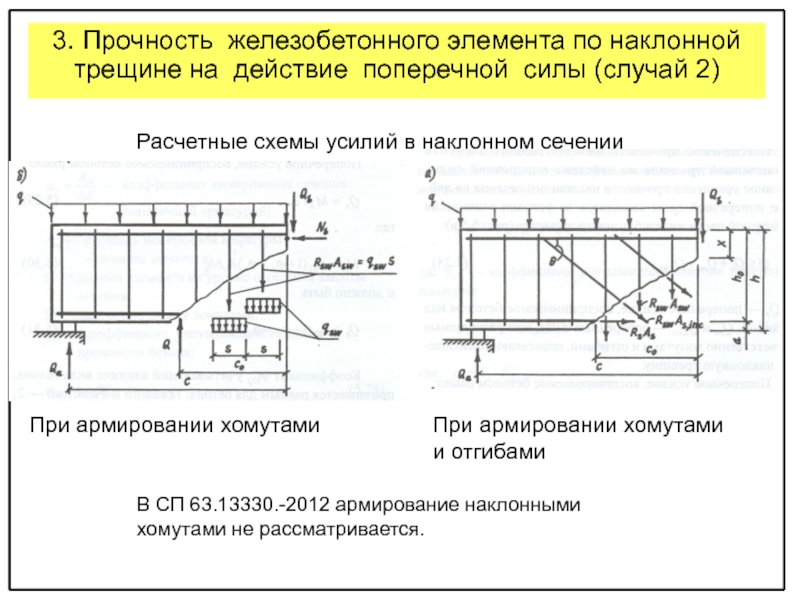
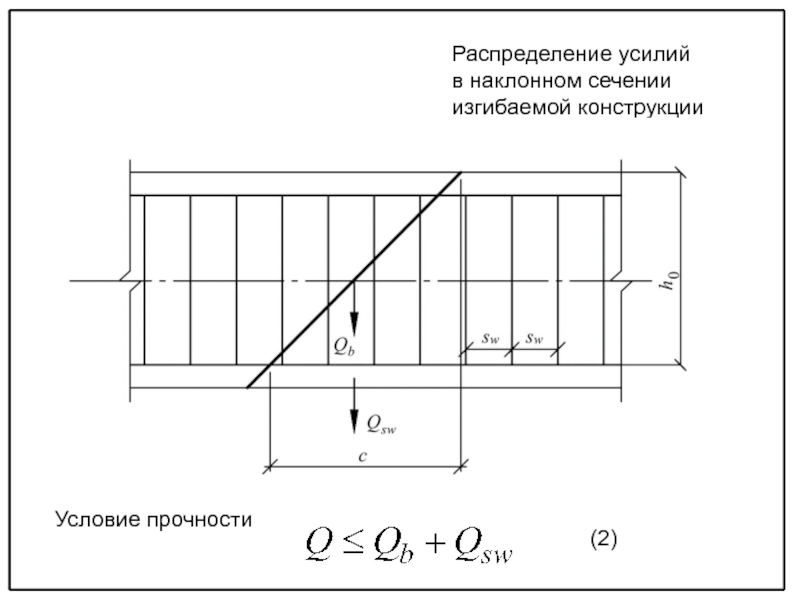
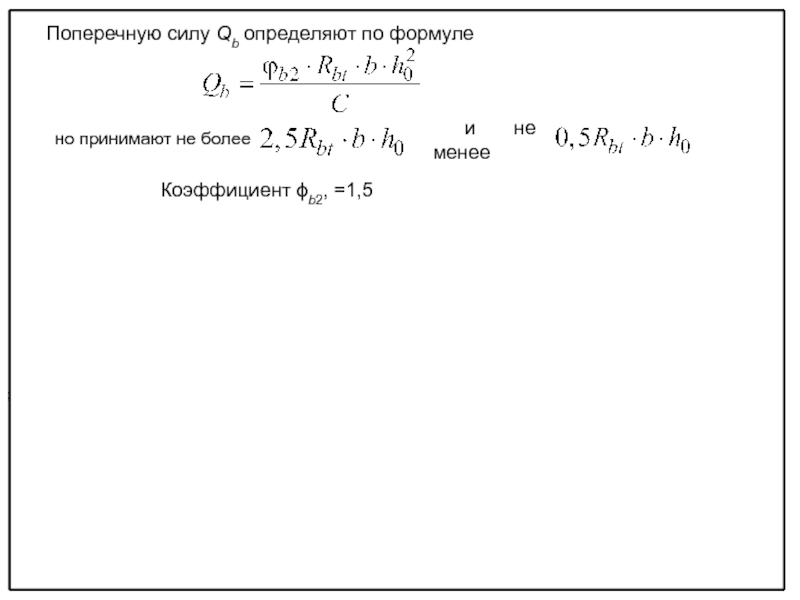
прочности изгибаемых элементов по наклонным сечениям
Тема

3. Расчет железобетонных изгибаемых элементов по прочности

Дисциплина
«ЖЕЛЕЗОБЕТОННЫЕ КОНСТРУКЦИИ»
Часть I
Курс лекций

Составитель: В. В. Родевич

Томский государственный архитектурно-строительный университет Кафедра «Железобетонные и каменные конструкции»Лекция 10.Расчет прочности изгибаемых элементов по наклонным сечениям

Слайд 2Вопросы:
Физические основы сопротивления железобетонных конструкций по наклонным сечениям

Расчет на действие

поперечной силы по наклонной полосе между наклонными трещинами

Прочность железобетонного

элемента по наклонной трещине на действие поперечной силы

Условия прочности наклонных сечений на действие изгибающего момента

Расчёт элементов без поперечной арматуры

Расчёт поперечных стержней

Расчёт отдельных отгибов

Вопросы:Физические основы сопротивления железобетонных конструкций по наклонным сечениямРасчет на действие поперечной силы по наклонной полосе между наклонными

Слайд 31. Физические основы сопротивления железобетонных конструкций по наклонным сечениям
а –

главные напряжения в бетоне около опоры
б – характер разрушения

балки по наклонному сечению

1. Физические основы сопротивления железобетонных конструкций по наклонным сеченияма – главные напряжения в бетоне около опоры б

Слайд 4

Слайд 5Случай 1
3 случая разрушения изгибаемых элементов
по наклонным сечениям
Разрушение от

действия изгибающего момента
Случай 2
Разрушение от действия поперечной силы
Разрушение

по сжатой полосе бетона между наклонными трещинами

Случай 3

Случай 13 случая разрушения изгибаемых элементов по наклонным сечениямРазрушение от действия изгибающего момента Случай 2Разрушение от действия

Слайд 61 - критическая наклонная трещина;
2 - дополнительные наклонные трещины;

3 - продольная трещина;
4 - раздавленный участок сжатой зоны

бетона;
c - расстояние от внутренней грани опоры до
вершины наклонной трещины

Характер разрушения изгибаемого элемента по наклонному сечению

при действии сосредоточенных сил

при загружении конструкции равномерно
распределённой нагрузкой

1 - критическая наклонная трещина; 2 - дополнительные наклонные трещины; 3 - продольная трещина; 4 - раздавленный

Слайд 72. Расчет на действие поперечной силы по наклонной полосе между

наклонными трещинами (случай 3)
Характер разрушения полосы бетона между наклонными трещинами

в балке двутаврового сечения:

1 - опасная наклонная трещина;

2 - раздавливание бетона

Предельное значение поперечной силы, действующей в нормальном сечении, расположенном на расстоянии не более чем hо от опоры

(1)

2. Расчет на действие поперечной силы по наклонной полосе между наклонными трещинами (случай 3)Характер разрушения полосы бетона

Слайд 83. Прочность железобетонного элемента по наклонной трещине на действие поперечной

силы (случай 2)
Расчетные схемы усилий в наклонном сечении
При армировании

хомутами
и отгибами

При армировании хомутами

В СП 63.13330.-2012 армирование наклонными хомутами не рассматривается.

3. Прочность железобетонного элемента по наклонной трещине на действие поперечной силы (случай 2)Расчетные схемы усилий в наклонном

Слайд 9Распределение усилий
в наклонном сечении
изгибаемой конструкции

Условие прочности

(2)

Слайд 10

Коэффициент ϕb2, =1,5
Поперечную силу Qb определяют по формуле

но принимают не

более
и не менее
;

Слайд 11

где φsw – коэффициент, принимаемый равным 0,75;
qsw – усилие в поперечной

арматуре на единицу длины элемента, равное

расчётное сопротивление хомутов и

отгибов при расчёте на действие поперечной силы
Rsw = 0.8 ⋅ Rs;
0.8 - коэффициент, учитывает неравномерное распределение напряжений в хомутах и отгибах по длине наклонного сечения;

Расчет производят для ряда расположенных по длине элемента наклонных сечений при наиболее опасной длине проекции наклонного сечения С.

где φsw – коэффициент, принимаемый равным 0,75;qsw – усилие в поперечной арматуре на единицу длины элемента, равное расчётное

Слайд 12Поперечную арматуру учитывают в расчете, если соблюдается условие
qsw≥
.
Допускается учитывать

поперечную арматуру и при невыполнении этого условия, если в условии

(2) принимать

Поперечную арматуру учитывают в расчете, если соблюдается условиеqsw≥ .Допускается учитывать поперечную арматуру и при невыполнении этого условия,

Разделы презентаций

Расчет элементов по наклонным сечениям

Содержание

Слайды и текст этой презентации

Слайд 1Томский государственный архитектурно-строительный университет
Кафедра
«Железобетонные и каменные конструкции»
Лекция 10.
Расчет

прочности изгибаемых элементов по наклонным сечениям
Тема

Слайд 2Вопросы:
Физические основы сопротивления железобетонных конструкций по наклонным сечениям

Расчет на действие

поперечной силы по наклонной полосе между наклонными трещинами

Прочность железобетонного

Слайд 31. Физические основы сопротивления железобетонных конструкций по наклонным сечениям
а –

главные напряжения в бетоне около опоры
б – характер разрушения

Слайд 4

Слайд 5Случай 1
3 случая разрушения изгибаемых элементов
по наклонным сечениям
Разрушение от

действия изгибающего момента
Случай 2
Разрушение от действия поперечной силы
Разрушение

Слайд 61 - критическая наклонная трещина;
2 - дополнительные наклонные трещины;

3 - продольная трещина;
4 - раздавленный участок сжатой зоны

Слайд 72. Расчет на действие поперечной силы по наклонной полосе между

наклонными трещинами (случай 3)
Характер разрушения полосы бетона между наклонными трещинами

Слайд 83. Прочность железобетонного элемента по наклонной трещине на действие поперечной

силы (случай 2)
Расчетные схемы усилий в наклонном сечении
При армировании

Слайд 9Распределение усилий
в наклонном сечении
изгибаемой конструкции

Условие прочности

(2)

Слайд 10

Коэффициент ϕb2, =1,5
Поперечную силу Qb определяют по формуле

но принимают не

более
и не менее
;

Слайд 11

где φsw – коэффициент, принимаемый равным 0,75;
qsw – усилие в поперечной

арматуре на единицу длины элемента, равное

расчётное сопротивление хомутов и

Слайд 12Поперечную арматуру учитывают в расчете, если соблюдается условие
qsw≥
.
Допускается учитывать

поперечную арматуру и при невыполнении этого условия, если в условии

Слайд 13

Слайд 14

Слайд 15

Слайд 16

Слайд 17

Обратная связь

Что такое TheSlide.ru?

Разделы презентаций

Расчет элементов по наклонным сечениям

Содержание

Слайды и текст этой презентации

Слайд 1Томский государственный архитектурно-строительный университет Кафедра «Железобетонные и каменные конструкции»Лекция 10.Расчет

прочности изгибаемых элементов по наклонным сечениям Тема

Слайд 2Вопросы:Физические основы сопротивления железобетонных конструкций по наклонным сечениямРасчет на действие

поперечной силы по наклонной полосе между наклонными трещинами Прочность железобетонного

Слайд 31. Физические основы сопротивления железобетонных конструкций по наклонным сеченияма –

главные напряжения в бетоне около опоры б – характер разрушения

Слайд 4

Слайд 5Случай 13 случая разрушения изгибаемых элементов по наклонным сечениямРазрушение от

действия изгибающего момента Случай 2Разрушение от действия поперечной силы Разрушение

Слайд 61 - критическая наклонная трещина; 2 - дополнительные наклонные трещины;

3 - продольная трещина; 4 - раздавленный участок сжатой зоны

Слайд 72. Расчет на действие поперечной силы по наклонной полосе между

наклонными трещинами (случай 3)Характер разрушения полосы бетона между наклонными трещинами

Слайд 83. Прочность железобетонного элемента по наклонной трещине на действие поперечной

силы (случай 2)Расчетные схемы усилий в наклонном сечении При армировании

Слайд 9Распределение усилий в наклонном сечении изгибаемой конструкцииУсловие прочности (2)

Слайд 10Коэффициент ϕb2, =1,5Поперечную силу Qb определяют по формуле но принимают не

более и не менее ;

Слайд 11где φsw – коэффициент, принимаемый равным 0,75;qsw – усилие в поперечной

арматуре на единицу длины элемента, равное расчётное сопротивление хомутов и

Слайд 12Поперечную арматуру учитывают в расчете, если соблюдается условиеqsw≥ .Допускается учитывать

поперечную арматуру и при невыполнении этого условия, если в условии

Слайд 13

Слайд 14

Слайд 15

Слайд 16

Слайд 17

Похожие презентации

Обратная связь

Что такое TheSlide.ru?

Слайд 1Томский государственный архитектурно-строительный университет
Кафедра
«Железобетонные и каменные конструкции»
Лекция 10.
Расчет

прочности изгибаемых элементов по наклонным сечениям
Тема

Слайд 2Вопросы:
Физические основы сопротивления железобетонных конструкций по наклонным сечениям

Расчет на действие

поперечной силы по наклонной полосе между наклонными трещинами

Прочность железобетонного

Слайд 31. Физические основы сопротивления железобетонных конструкций по наклонным сечениям
а –

главные напряжения в бетоне около опоры
б – характер разрушения

Слайд 5Случай 1
3 случая разрушения изгибаемых элементов
по наклонным сечениям
Разрушение от

действия изгибающего момента
Случай 2
Разрушение от действия поперечной силы
Разрушение

Слайд 61 - критическая наклонная трещина;
2 - дополнительные наклонные трещины;

3 - продольная трещина;
4 - раздавленный участок сжатой зоны

наклонными трещинами (случай 3)
Характер разрушения полосы бетона между наклонными трещинами

силы (случай 2)
Расчетные схемы усилий в наклонном сечении
При армировании

Слайд 9Распределение усилий
в наклонном сечении
изгибаемой конструкции

Условие прочности

(2)

Слайд 10

Коэффициент ϕb2, =1,5
Поперечную силу Qb определяют по формуле

но принимают не

более
и не менее
;

Слайд 11

где φsw – коэффициент, принимаемый равным 0,75;
qsw – усилие в поперечной

арматуре на единицу длины элемента, равное

расчётное сопротивление хомутов и

Слайд 12Поперечную арматуру учитывают в расчете, если соблюдается условие
qsw≥
.
Допускается учитывать