Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Распределение микроколичеств радиоактивных изотопов между двумя фазами
Содержание
- 1. Распределение микроколичеств радиоактивных изотопов между двумя фазами
- 2. Распределение микрокомпонента Между твердой и жидкой фазамиМежду
- 3. Распределение между твердой и жидкой фазами Соосаждение
- 4. Процессы соосажденияИзотопный носитель – нерадиоактивный изотоп данного
- 5. Изотопные носителиИдентичность свойств и поведения изотопов (избирательность)Критерий
- 6. Процессы соосаждения со специфическими носителямиПроцессы изоморфной сокристаллизации.Митчерлих,
- 7. Процессы соосаждения со специфическими носителямиИзоморфны вещества с
- 8. Изоморфизм (по Гольшмидту)У обоих соединений сумма зарядов
- 9. Наличие аналогии химических соединений (KCl - NaCl,
- 10. Смешанные кристаллы 1 рода (изоморфизм замещения, изодиморфизм,
- 11. Гриммовские смешанные кристаллы:Ba (Sr, Pb)SO4 – K
- 12. Природные изоморфные ряды
- 13. Na(Li,Al)3Al6[(OH)4|(BO3)Si6O18] Многие драгоценные камни отличаются разнообразием своих
- 14. Соосаждение радионуклидов со специфическими носителямиИзбирательность по отношению
- 15. Применение специфических носителейУстановление принадлежности радиоактивного нуклида, выделенного
- 16. Закономерности соосаждения1926 г., Хан (Ган): 2 вида
- 17. Закономерности соосажденияПравило Гана: Радиоактивный элемент или другой
- 18. Закономерности соосажденияЗакон Хлопина: Если два вещества являютсяизоморфными
- 19. Закономерности соосажденияx – количество микрокомпонента в кристаллахx0
- 20. Закономерности соосажденияЗакон Бертло-Нернста Уравнение Гендерсона-КречекаD – коэффициент
- 21. Термодинамически равновесное распределение при соосаждении Aт +
- 22. Термодинамическая активность чистой твердой фазы ат =
- 23. При сокристаллизации раствор насыщенпо отношению к макрокомпонентуДля
- 24. Термодинамически равновесное распределение при соосаждении D –
- 25. При малых концентрациях компонента В можно принять
- 26. При отсутствии нижней границы смешиваемости закон наблюдается
- 27. Влияние различных факторов на процесс соосажденияТемператураИз соотношений:Ат
- 28. Влияние различных факторов на процесс соосажденияСостав жидкой
- 29. Влияние различных факторов на процесс соосажденияСостав жидкой
- 30. Влияние различных факторов на процесс соосажденияСостав жидкой
- 31. Влияние различных факторов на процесс соосажденияСостав твердой
- 32. Влияние различных факторов на процесс соосажденияНаличие второго
- 33. Кинетика процессов соосажденияПроцесс для микрослоя кристалла описывается
- 34. Кинетика процессов соосажденияПри 0 1концентрация микрокомпонента в
- 35. В процессе роста кристаллов соосаждение описывается:dx/dy =
- 36. Три режима кристаллизацииКинетический режим кристаллизации:p >> п
- 37. При достаточном времени для установленияравновесия, постоянной ионной
- 38. 2. Диффузионный режим кристаллизацииp >> п >>т
- 39. 3. Миграционный режим кристаллизацииp >> п >>т
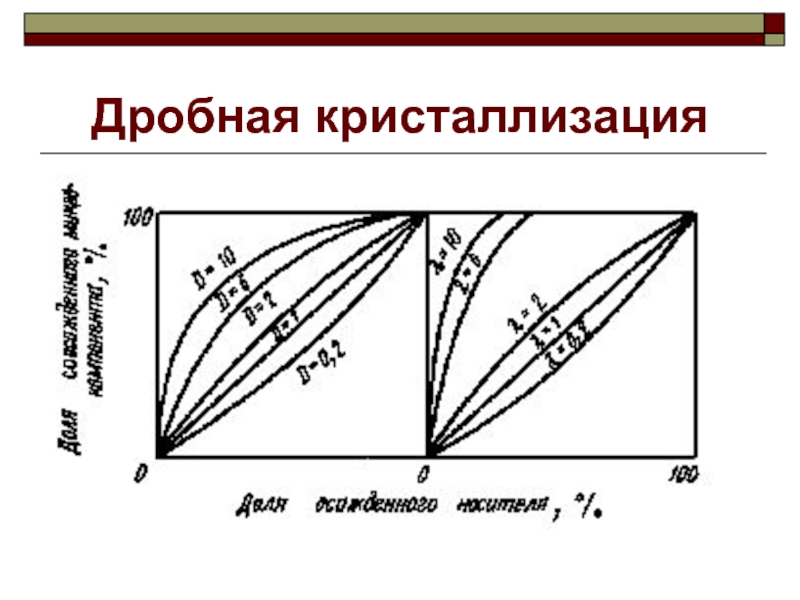
- 40. Дробная кристаллизацияДля отделения радиоактивных элементов от специфических
- 41. Дробная кристаллизация
- 42. Распределение между твердой фазой и расплавомЛогарифмическое распределение
- 43. Распределение между твердой фазой и расплавомИзменение активности
- 44. Распределение между твердой и газовой фазамиЗакономерности установлены
- 45. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Распределение микрокомпонента
Между твердой и жидкой фазами
Между твердой фазой и
расплавом
и раствором Слайд 3Распределение между твердой и жидкой фазами
Соосаждение – процесс переноса
микрокомпонента из раствора в твердую фазу, образуемую веществом носителя.
Сокристаллизация –
соосаждение с кристаллическими осадками, при котором микрокомпонент распределяется по всему объему твердой фазы, участвуя в построении кристаллической решетки макрокомпонента.Адсорбция – процессы осаждения микрокомпонента на поверхности твердой фазы макрокомпонента (включая внутренюю поверхность).
Слайд 4Процессы соосаждения
Изотопный носитель – нерадиоактивный изотоп данного химического элемента (Cs
стаб. для 137Сs и 134Cs)
Неизотопный носитель – элемент, сходный по
своим свойствам с радиоактивным (Сa для Sr) или несходный элемент, но соосаждение сопровождается образованием осадков с сильноразвитой поверхностью (Fe для Pu, Am). Специфические носители
Неспецифические носители
Слайд 5Изотопные носители
Идентичность свойств и поведения изотопов (избирательность)
Критерий соосаждения – практическая
невозможность изменения изотопного состава твердой фазы обычными физико-химическими методами
Основная закономерность:
доля соединения радиоактивного изотопа, переходящего в твердую фазу, равна доле соединения изотопного носителя, переходящего в эту фазу. Независимость процессов соосаждения от концентрации радиоактивного изотопа, состава раствора, температуры, давления и др.
Невозможность отделения радиоактивного изотопа от носителя.
Слайд 6Процессы соосаждения со специфическими носителями
Процессы изоморфной сокристаллизации.
Митчерлих, 1819 г.: изоморфные
вещества сходны в химическом отношении, обладают одинаковой кристаллической структурой и
способны образовывать смешанные кристаллы.Современные представления: изоморфизм – свойство элементов замещать друг друга в кристаллической структуре при условии близости размеров и характера химической связи.
Слайд 7Процессы соосаждения со специфическими носителями
Изоморфны вещества с одинаковой кристаллической структурой.
Изовалентный
и гетеровалентный изоморфизм. Изовалентный - в структуре минерала замещаются элементы
равной валентности. Гетеровалентный - элементы разной валентности.Изодиморфизм: сходные по химическому составу вещества, но с разной кристаллической структурой могут образовывать смешанные кристаллы.
Слайд 8Изоморфизм (по Гольшмидту)
У обоих соединений сумма зарядов атомов, входящих в
их состав, и распределение зарядов одинаковы (SrSO4 и RaSO4)
Сумма зарядов
одинакова, но их распределение различно (SrSO4 и KClO4)Сумма зарядов неодинакова, но число атомов одинаково (TiO2 и МgF2).
Слайд 9Наличие аналогии химических соединений (KCl - NaCl, BaSO4 - KBF4)
Сходство
симметрии элементарных ячеек и близость их размеров.
KCl (а=6,28 Å):
непрерывный ряд
смешанных кристаллов с RbCl (а=6,54 Å),при повышенной температуре с NaCl (а=5,63 Å),
не образует с LiCl (а=5,13 Å).
Изоморфизм (по Гримму)
Слайд 10Смешанные кристаллы 1 рода (изоморфизм замещения, изодиморфизм, KCl - RbCl)
Смешанные
кристаллы 2 рода (изоморфизм внедрения, атомы второго компонента занимают пустоты
в решетке первого, С в металлическом Fe).Смешанные кристаллы, образующиеся заполнением пространства (изоморфизм заполнения пространства): замещение одного атома на другой и заполнение пространства, YF3 c CaF2.
Изоморфизм
Слайд 11Гриммовские смешанные кристаллы:
Ba (Sr, Pb)SO4 – K (NH4, Na)MnO4
Характерна нижняя
граница смешиваемости
Аномальные смешанные кристаллы
Не отвечают изоморфизму по Гримму-Гольшмидту.
NH4Cl - FeCl3,
RaF2 – LaF2Нижняя и верхняя границы смешиваемости,
Неограниченная смешиваемость (образование
комплексных соединений): MnCl2 – NH4Cl
2 NH4Cl* MnCl2* 2H2O
Изоморфизм
Слайд 13Na(Li,Al)3Al6[(OH)4|(BO3)Si6O18]
Многие драгоценные камни отличаются разнообразием своих цветов, но первенство
принадлежит турмалину.
Турмалин является изоморфным минералом и относится к группе боросиликатов.
В странах Средиземноморья турмалин известен с античных времен, но в Европу из Цейлона его завезли голландцы в 1703 году.
Слайд 14Соосаждение радионуклидов со специфическими носителями
Избирательность по отношению к радиоактивному элементу
Отсутствие
нижней границы смешиваемости
Зависимость степени переноса радиоактивного элемента в твердую фазу
от условий образования кристаллической фазыСлайд 15Применение специфических носителей
Установление принадлежности радиоактивного нуклида, выделенного из природных объектов
(например, Франция) или полученного в результате ядерных реакций (например, технеция),
определенному радиоактивному элементу.Установление химической формы существования радиоактивных элементов в крайне разбавленных растворах.
Избирательное выделение и концентрирование радиоактивных элементов.
Подбор систем с максимальным значением коэффициента кристаллизации и минимальной растворимостью соединения-носителя. Для исключения адсорбционных процессов - создание условий, обеспечивающих образование кристаллической фазы с малоразвитой поверхностью.
Слайд 16Закономерности соосаждения
1926 г., Хан (Ган): 2 вида соосаждения, истинное и
адсорбционное.
Истинное: микрокомпонент распределяется по всему объему твердой фазы.
Адсорбционное: по поверхности
осадка.Признак истинного соосаждения: постоянство коэффициента распределения, относительно медленное установление равновесия в системе «осадок – раствор», отсутствие влияния заряда поверхности на процесс.
Слайд 17Закономерности соосаждения
Правило Гана:
Радиоактивный элемент или другой химический
элемент, находящийся в
следовых количествах,
переходит из раствора в твердую кристаллическую
фазу лишь в том
случае, если он может приниматьучастие в построении кристаллической решетки
макрокомпонента, т.е. микрокомпонент с анионом
твердой фазы образует соединение,
кристаллизующееся изоморфно соответствующим
соединениям макрокомпонента.
Слайд 18Закономерности соосаждения
Закон Хлопина:
Если два вещества являются
изоморфными или изодиморфными и
концентрация
одного из них мала, то
распределение микрокомпонента между
кристаллической фазой и раствором
припостоянной температуре и давлении
характеризуется постоянной величиной и
не зависит от количественного
соотношения фаз.
Слайд 19Закономерности соосаждения
x – количество микрокомпонента в кристаллах
x0 – общее количество
микрокомпонента в системе
m– плотность кристаллов
mm – масса кристаллов
p – плотность
раствораmр – масса раствора
Kx – константа Хлопина
Слайд 20Закономерности соосаждения
Закон Бертло-Нернста
Уравнение Гендерсона-Кречека
D – коэффициент кристаллизации, x0 x
- микрокомпонент в системе и кристаллах, y0 y - макрокомпонент
в системе и кристаллахСлайд 21Термодинамически равновесное распределение при соосаждении
Aт + Bр
Aр + Bт
При равновесии: Ат=Ар
Вт=Вр Ат + Вр =Ар+ Вт
i = i° + RT ln ai
аi – термодинамическая активность
Стандартные состояния:
1. Для любого компонента твердой фазы в чистом виде
ai = xi fi
xi – мольная доля компонента в твердой фазе,
fi - коэффициент термодинамической активности компонента в твердой фазе
2. Для любого компонента в жидком растворе его состояние в гипотетическом идеальном растворе
ai = mi i
mi – моляльная доля компонента в растворе,
i - коэффициент термодинамической активности компонента в растворе.
Слайд 22
Термодинамическая активность чистой твердой фазы ат = 1
Для насыщенных растворов
чистых компонентов:
Термодинамически равновесное распределение при соосаждении
Слайд 23При сокристаллизации раствор насыщен
по отношению к макрокомпоненту
Для бесконечно разбавленных растворов
хА1, fА 1
D0 – истинная константа фракционирования. Зависит от температуры,
термодинамической активности макрокомпонента в растворе.
Термодинамически равновесное распределение при соосаждении
Слайд 24Термодинамически равновесное распределение при соосаждении
D – коэффициент кристаллизации в
системе из веществ А и В
Для идеальных растворов коэффициенты
активности =1 , К = D Слайд 25При малых концентрациях компонента В можно принять хА 1
Мольная доля
компонента В в твердой фазе при хB
моляльных концентраций компонентов А и В в растворе равно отношению числа молей каждого компонента:Уравнение Гендерсона-Кречека:
Термодинамически равновесное распределение при соосаждении
Слайд 26При отсутствии нижней границы смешиваемости закон наблюдается до концентрации 10-4
моль/л.
В системах, в которых отношение коэффициентов активностей не меняется с
изменением концентрации, закон соблюдается при любых концентрациях.При наличии верхней границы смешиваемости при малых концентрациях микрокомпонента закон соблюдается не выше верхней границы смешиваемости.
Термодинамически равновесное распределение при соосаждении
Слайд 27Влияние различных факторов на процесс соосаждения
Температура
Из соотношений:
Ат + Вр =Ар+
Вт
i = i° + RT ln ai
К = exp [((°Вр
- °Вт) - (°Aр - °Aт))/RTИзменение химического потенциала:
Δi = ΔHi - T ΔSi
Для изоморфных веществ: ΔSA = ΔSB
К= exp (- ΔH°/RT)
С ростом T: в ряде случаев D растет, остается неизменным или изменяется по более сложному закону.
В большинстве случаев – уменьшается.
Слайд 28Влияние различных факторов на процесс соосаждения
Состав жидкой фазы
Правило Хлопина:
При
изменении состава жидкой фазы коэффициент кристаллизации
практически не меняется, если отношение
термодинамической активностиионов макро- и микрокомпонентов остается неизменным.
Если изменение состава жидкой фазы влечет за собой неодинаковое
изменение термодинамической активности ионов макро- и
микрокомпонентов в силу комплексообразования или образования
недиссоциирующих соединений или по каким-либо другим причинам и
если происходит преимущественное уменьшение термодинамической
активности ионов макрокомпонента, т.е. отношение термодинамических
активностей ионов макро- и микрокомпонента падает, то значения Kх и D
возрастают.
Слайд 29Влияние различных факторов на процесс соосаждения
Состав жидкой фазы
Константа Хлопина обратно
пропорциональна общей концентрации
макрокомпонента в растворе.
Коэффициент D c изменением концентрации макрокомпонента
меняется
сравнительно мало.Если к раствору добавлено вещество, имеющее одинаковый с
макрокомпонентом анион, то при изоморфной сокристаллизации Кх
растет, а D практически постоянна.
Изменение концентраций микрокомпонента в пределах концентраций
(до 0,01 М) практически не влечет изменения Кх и D.
Слайд 30Влияние различных факторов на процесс соосаждения
Состав жидкой фазы
На величину коэффициента
кристаллизации влияет присутствие комплексообразователей:
K и K’ – константы устойчивости комплексов
микро- и макрокомпонентаПри [AC] >> [A] D = Dk (K/K’)
Слайд 31Влияние различных факторов на процесс соосаждения
Состав твердой фазы
Плавное изменение состава
твердой фазы вызывает плавное
изменение Кх и D. При резком изменении
состава твердой фазы Кхи D изменяются скачкообразно.
Растворитель
Изменение растворителя вызывает изменение термодинамической
активности компонентов раствора.
Rb (K) Cl – H2O D=0,87
Rb (K) Cl – C2H5OH D=0,50
Rb (K) Cl – CH3COCH3 D=0,31
Слайд 32Влияние различных факторов на процесс соосаждения
Наличие второго микрокомпонента.
Если в растворе
присутствуют два не взаимодействующих друг с
другом микрокомпонента и внедрение их
в кристаллическую решеткумакрокомпонента не вызывает изменение числа дефектов решетки,
то их распределение происходит независимо друг от друга.
Если катион второго компонента имеет иную степень окисления, чем
катион макрокомпонента, то его внедрение в кристаллическую
решетку вызывает образование дополнительных дефектов, которые
ведут себя подобно примеси и влияют на величину коэффициента
распределения первого компонента.
Слайд 33Кинетика процессов соосаждения
Процесс для микрослоя кристалла описывается дифференциальным
уравнением:
Уравнение Дернера-Госкинса
Логарифмическое правило:
логарифм отношения концентрации
микрокомпонента в растворе до кристаллизации к его концентрации
после
кристаллизации, деленный на логарифм отношенияконцентрации макрокомпонента в растворе до кристаллизации к его
концентрации в растворе после кристаллизации, есть величина
постоянная.
Слайд 34Кинетика процессов соосаждения
При 0
центра кристалла к периферии.
При 0 >1концентрация микрокомпонента в кристаллах
возрастает от
центра кристалла к периферии.Логарифмическое и термодинамическое распределение микрокомпонента
являются предельным случаем.
При распределении микрокомпонента в условиях термодинамического
равновесия раствора со всей массой кристалла постоянным является
коэффициент кристаллизации D, а в условиях логарифмического
распределения - 0 .
Слайд 35В процессе роста кристаллов соосаждение описывается:
dx/dy = (x,у) F (cp)
x,у
– количество микро- и макрокомпонента в твердой фазе.
(x,у) – коэффициент
распределения между раствором, прилегающим кповерхности твердой фазы, и кристаллом в момент времени t.
сp – средняя концентрация микрокомпонента в растворе, сp’ – концентрация
микрокомпонента в растворе у поверхности кристалла,
Вид функций (x,у) и F (cp) зависит от:
Скорости перемещения частиц микрокомпонента из объема раствора к
поверхности кристалла (p )
Скорости перехода микрокомпонента через поверхность раздела фаз (п)
Скорости миграции микрокомпонента в твердой фазе (т)
Кинетика процессов соосаждения
Слайд 36Три режима кристаллизации
Кинетический режим кристаллизации:
p >> п >>т = 0
сp’ = сp
Поступление микрокомпонента из
раствора кповерхности твердой фазы идет со много большей
скоростью, чем переход через поверхность раздела
фаз, миграция в твердой фазе отсутствует.
Концентрация микрокомпонента у поверхности = его
средней концентрации в растворе.
dx/dy = (x,у) cp
Кинетика процессов соосаждения
Слайд 37При достаточном времени для установления
равновесия, постоянной ионной силе,
активности микрокомпонента (x,у)
=const.
x/y = 0 cp
Такой процесс осуществляется при
соосаждении путем сливания двух
растворов. Кинетика процессов соосаждения
Слайд 382. Диффузионный режим кристаллизации
p >> п >>т = 0
сp’ не равен сp
Поступление микрокомпонента из раствора к поверхности
лимитируется диффузией
его в растворе.(x,у) = 0 имеет постоянное равновесное значение.
Соосаждение в процессе роста кристаллов в диффузионном
режиме может приводить как к равномерному распределению
микрокомпонента, так и неравномерному распределению.
Кинетика процессов соосаждения
Слайд 393. Миграционный режим кристаллизации
p >> п >>т >> 0
сp’ = сp
Поступление микрокомпонента из раствора к поверхности твердой
фазы идет
со много большей скоростью, чем переход черезповерхность раздела фаз, миграция в твердой фазе существенно
больше нуля.
Концентрация микрокомпонента у поверхности = его средней
концентрации в растворе.
В предельном случае, в котором каждый вновь образующийся слой
приходит в термодинамическое равновесие с раствором, кинетика
процесса распределения описывается:
Кинетика процессов соосаждения
Слайд 40Дробная кристаллизация
Для отделения радиоактивных элементов от специфических носителей.
Проведение большого
числа стадий кристаллизации с разделением на каждой стадии жидкой и
твердой фаз.Если D > 1, то осадки будут обогащаться, а растворы обедняться радиоактивным элементом.
Процесс дробной кристаллизации характеризуется обычно не коэффициентом кристаллизации, а коэффициентом обогащения твердой фазы
Коэффициент обогащения зависит от коэффициента кристаллизации, возрастает с увеличением D, и осаждаемой доли носителя.
Слайд 42Распределение между твердой фазой и расплавом
Логарифмическое распределение не наблюдается ни
при каких условиях.
Коэффициент D не зависит от количества выделенной твердой
фазы.Константа 0 непрерывно возрастает с увеличением количества выделенной твердой фазы.
Равновесие расплав - кристаллы устанавливается быстро. Причины: аналогия структуры расплава и кристаллов, отсутствие сольватации ионов.
Скорость установления равновесия повышается с увеличением температуры.
Механизм установления равновесия: быстрая перекристаллизация твердой фазы в расплаве, а не диффузия.
Слайд 43Распределение между твердой фазой и расплавом
Изменение активности компонентов расплава изменяет
величину коэффициента кристаллизации D. При добавлении к расплаву веществ, образующихся
с микрокомпонентом комплексные соединения, т.е. снижающих активную концентрацию микрокомпонента, коэффициент D падает.Снижение активной концентрации макрокомпонента приводит к увеличению коэффициента D.
Скачкообразное изменение D с изменением состава расплава или температуры свидетельствует об образовании новой твердой фазы.
Для большинства изученных систем коэффициент кристаллизации меньше 1, т.е. в системах «расплав-кристаллы» микрокомпонентом обогащается расплав.
Слайд 44Распределение между твердой и газовой фазами
Закономерности установлены на примере радона.
Радон
сокристаллизуется с НBr (Rn- НBr*2C6H5CH3),
H2S (Rn- H2S *2C6H5CH3)
SO2 (Rn-
SO2 *2C6H5OH, Rn- SO2 *6H2O)Смешанные кристаллы представляют собой клатратные соединения, в которых радон наряду с НBr, H2S, SO2 занимает пустоты в решетке, состоящей из молекул воды, фенола или толуола.
Распределение радона между клатратными соединениями и газовой фазой подчиняются закону Хлопина.
Другие благородные газы образуют смешанные кристаллы в системах: элемент - H2S *2C6H5OH, SO2 *6H2O.
Наибольший коэффициент распределения характерен для тяжелых благородных газов.












![Распределение микроколичеств радиоактивных изотопов между двумя фазами Na(Li,Al)3Al6[(OH)4|(BO3)Si6O18] Многие драгоценные камни отличаются разнообразием своих цветов, но первенство принадлежит Na(Li,Al)3Al6[(OH)4|(BO3)Si6O18] Многие драгоценные камни отличаются разнообразием своих цветов, но первенство принадлежит турмалину.Турмалин является изоморфным минералом и относится](/img/tmb/4/324567/0e88c2683941fd36b47c811e921cac05-800x.jpg)