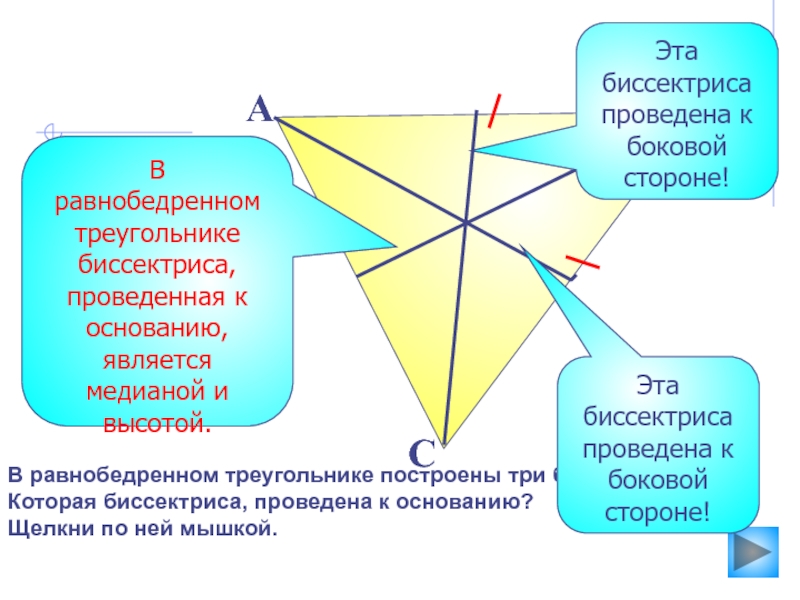
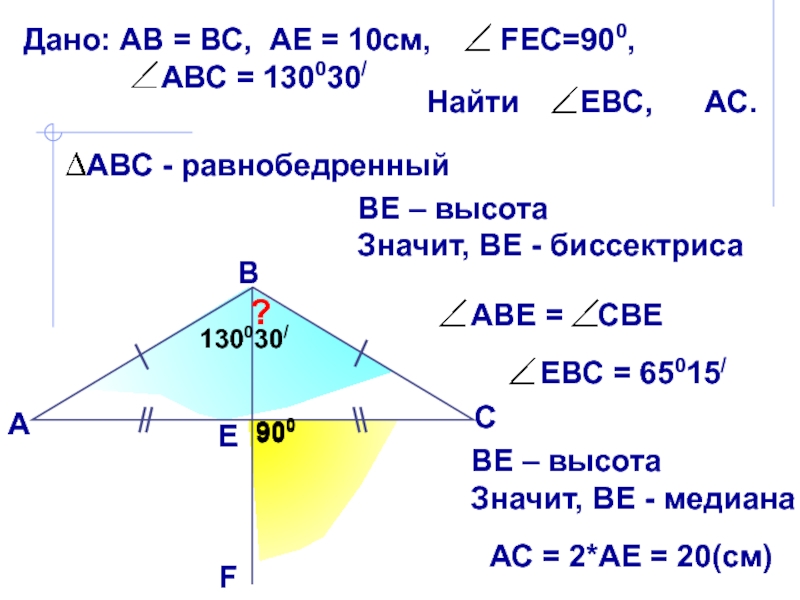
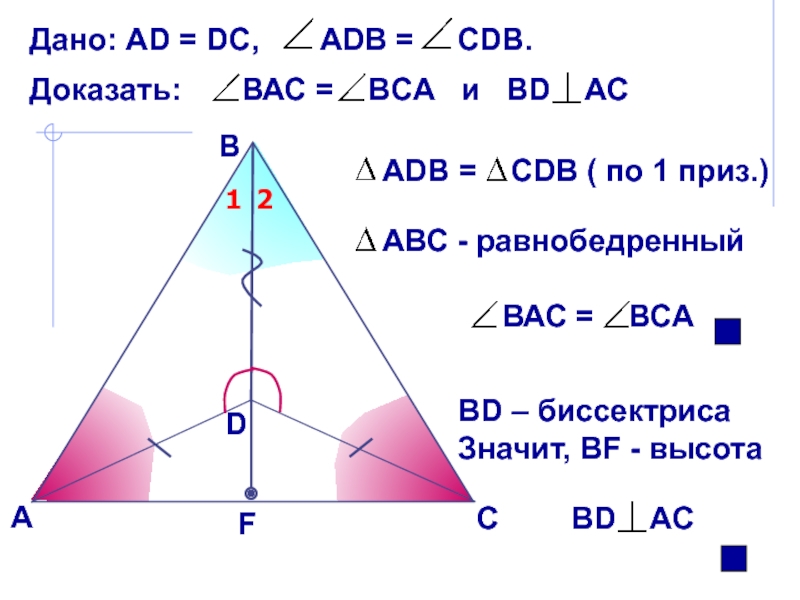
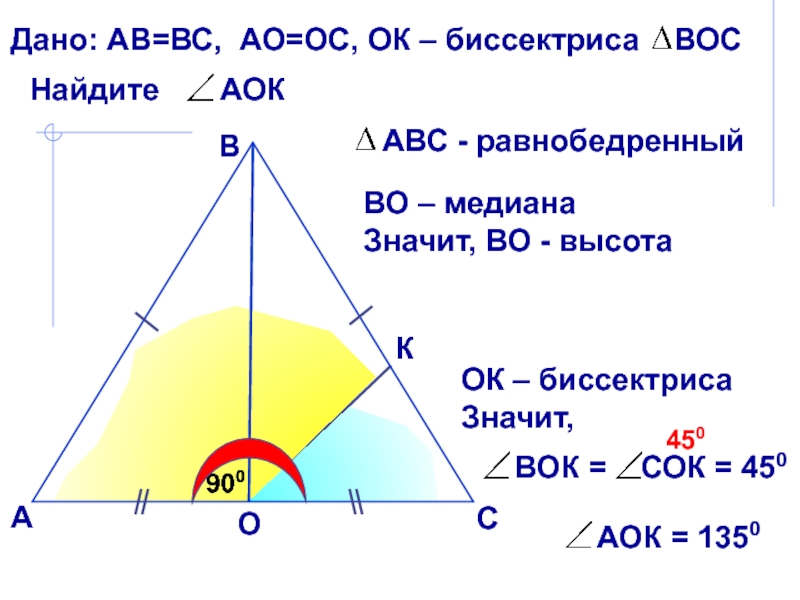
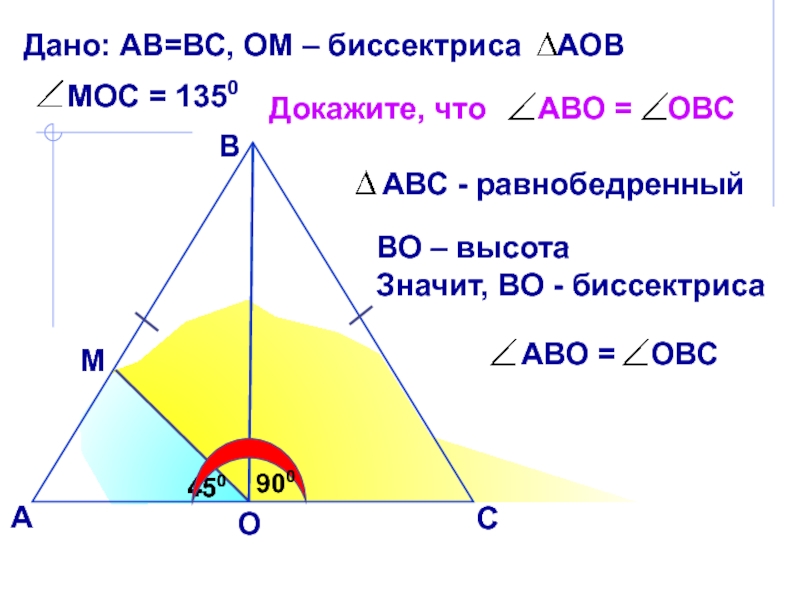
основанию?
Щелкни по ней мышкой.
А
С
В
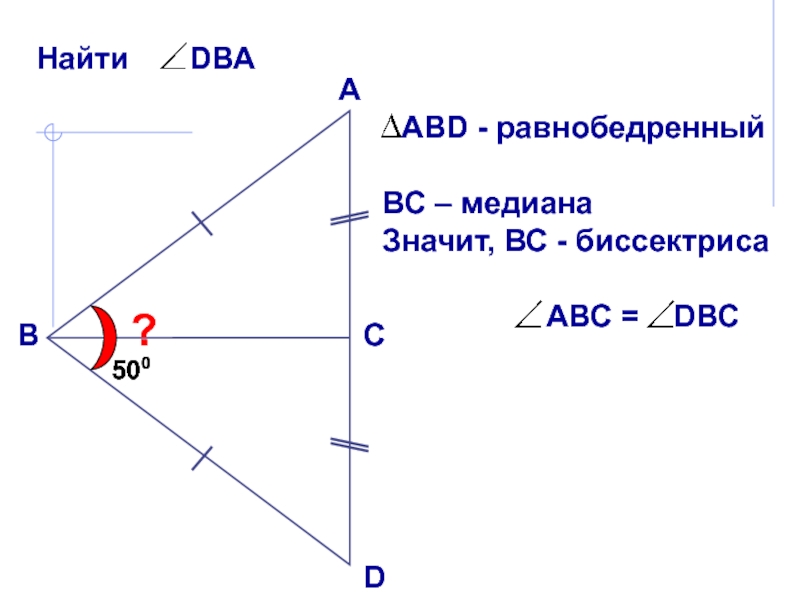
Эта биссектриса проведена к боковой стороне!
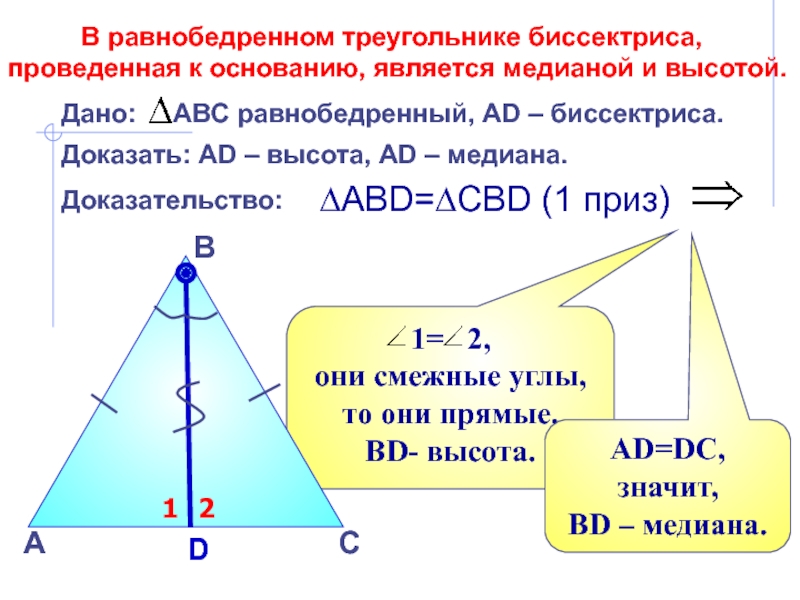
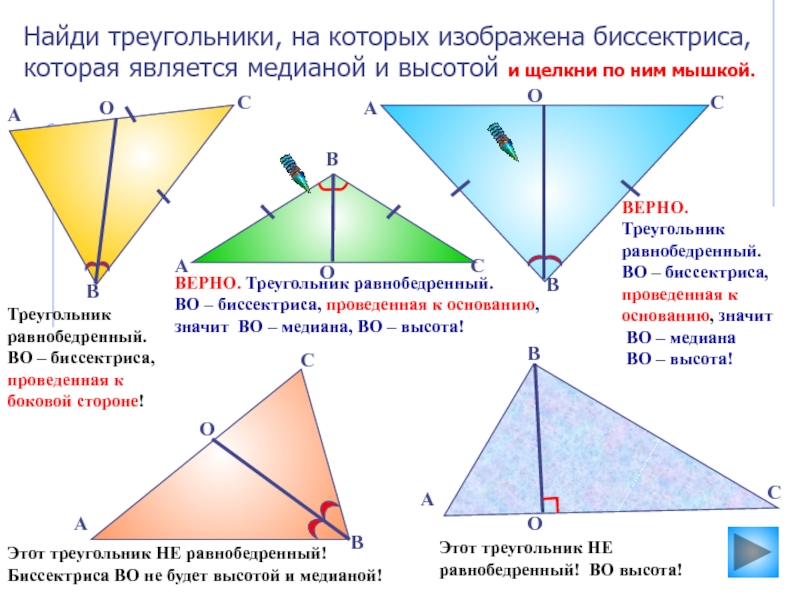
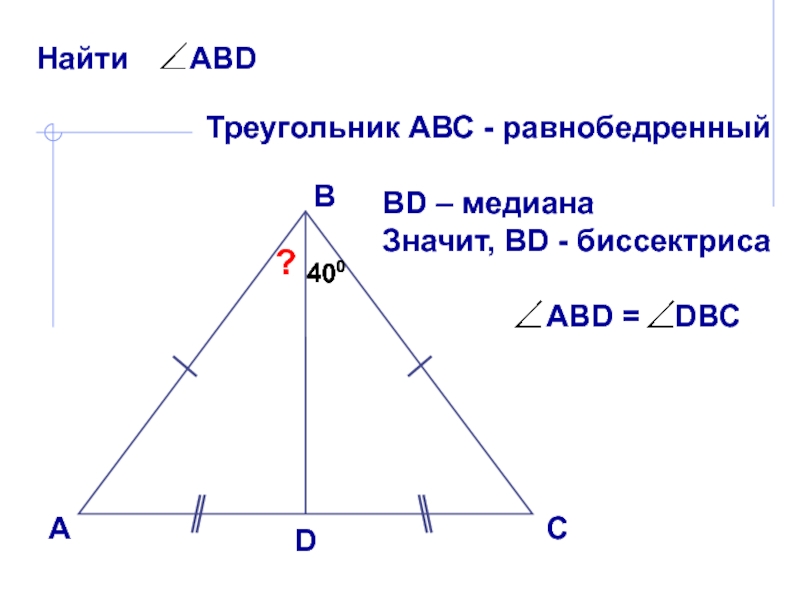
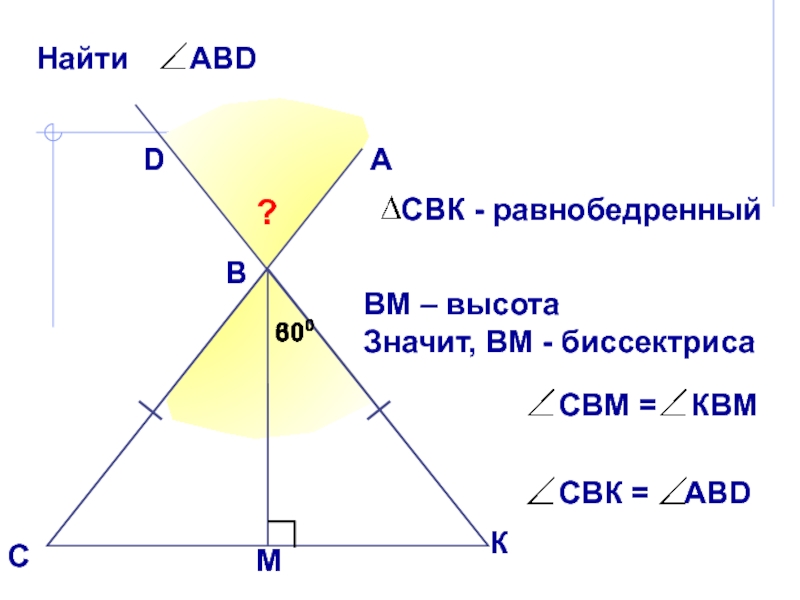
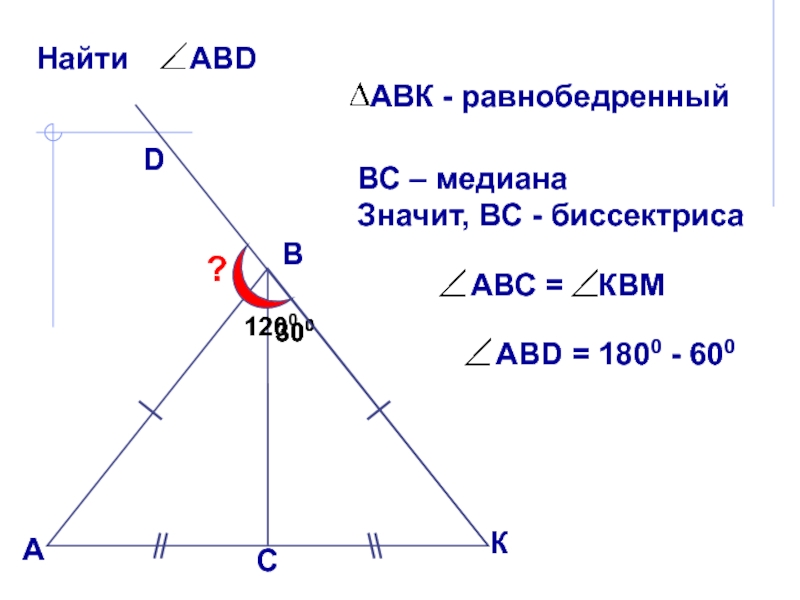
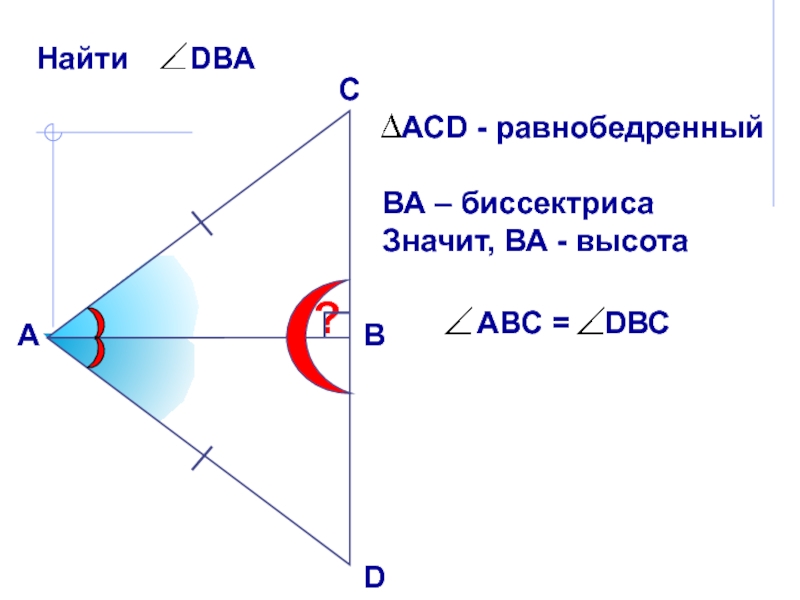
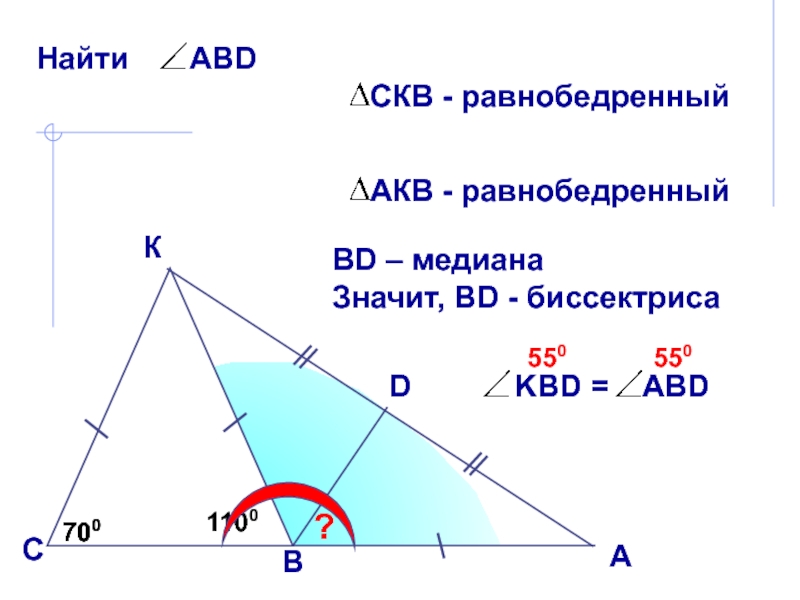
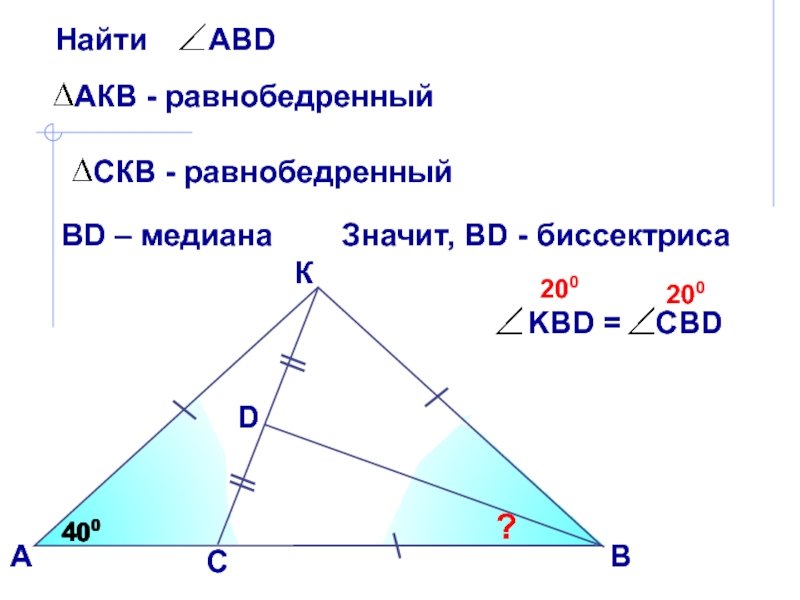
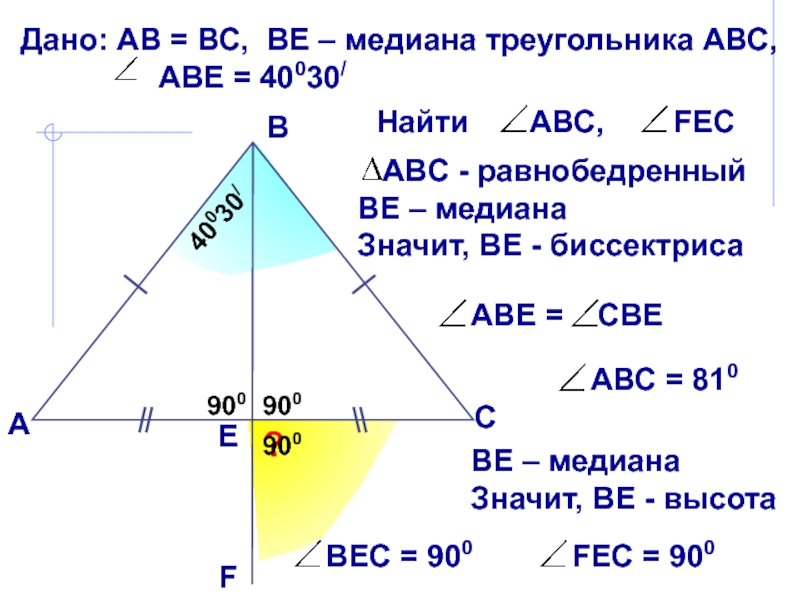
В равнобедренном
треугольнике биссектриса, проведенная к основанию, является медианой и высотой. Эта биссектриса проведена к боковой стороне!