Слайд 1Раздел 3. Оптические свойства веществ
Лекция 6. Классическая теория дисперсии.
Рассеяние света
6.1. Модель среды с дисперсией. Классическая теория. Комплексный показатель
преломления
6.2. Нормальная и аномальная дисперсии.
Поглощение волн. Закон Бугера
6.3. Фазовая скорость. Волновой пакет. Групповая скорость
6.4. Рассеяние света. Прохождение света через оптически неоднородную среду. Рэлеевское рассеяние.
Рассеяние Ми.
Рассеяние Мандельштама - Бриллюэна
Слайд 26.1. Модель среды с дисперсией. Классическая теория. Комплексный показатель преломления
Материальные среды, существующие в виде твердых тел, жидкостей и газов,
состоят из заряженных частиц - электронов и ионов, связанных между собой кулоновскими силами. При проникновении электромагнитной волны в материальную среду на заряженные частицы материальной среды действуют дополнительные силы, величина которых зависит от энергии электромагнитной волны, попавшей в материальную среду. С другой стороны, при ускоренном движении заряженных частиц происходит излучение электромагнитных волн. Таким образом, в материальной среде должно происходить взаимодействие электромагнитных волн с заряженными частицами, приводящее к изменению как характеристик свободных электромагнитных волн, распространяющихся в вакууме, так и закона движения электронов и ионов материальной среды.
При распространении электромагнитной волны в материальных средах происходит изменение характеристик электрического и магнитного полей. Свойства электромагнитных волн в материальной среде описываются с помощью уравнений Максвелла.
Как оказалось, свойства электромагнитных волн в материальной среде существенным образом зависят от значения их длины волны λ0 в вакууме.

Слайд 3Важной характеристикой материальной среды является её абсолютный показатель преломления n.
В простейших случаях показатель преломления является вещественным числом, большим единицы.
Показатель преломления характеризует изменение длины электромагнитной волны при попадании её из вакуума в материальную среду: n = λ0/λ (λ – длина электромагнитной волны в рассматриваемой материальной среде). Таким образом, при проникновении электромагнитной волны в материальную среду частота её не изменяется, а длина волны уменьшается.
Согласно классической теории Максвелла показатель преломления n в материальной среде связан с диэлектрической и магнитной проницаемостями соотношением: n2 = εμ. В 1672 г. Ньютоном были
выполнены экспериментальные исследования по изучению зависимости показателя преломления материальных сред от длины волны. Такое явление было названо дисперсией света.
Это явление обусловлено изменением
показателя преломления
материальной среды с
изменением длины волны λ0 исходного
электромагнитного излучения.
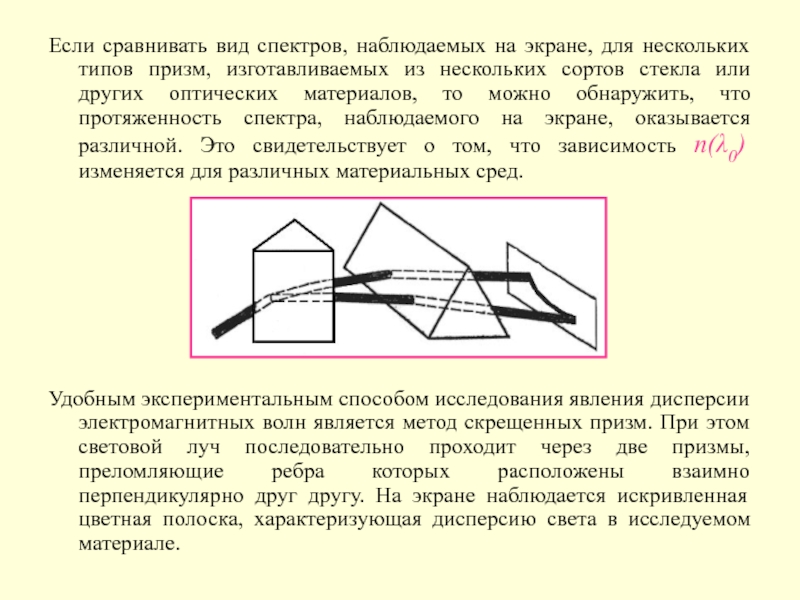
Слайд 4Если сравнивать вид спектров, наблюдаемых на экране, для нескольких типов
призм, изготавливаемых из нескольких сортов стекла или других оптических материалов,
то можно обнаружить, что протяженность спектра, наблюдаемого на экране, оказывается различной. Это свидетельствует о том, что зависимость n(λ0) изменяется для различных материальных сред.
Удобным экспериментальным способом исследования явления дисперсии электромагнитных волн является метод скрещенных призм. При этом световой луч последовательно проходит через две призмы, преломляющие ребра которых расположены взаимно перпендикулярно друг другу. На экране наблюдается искривленная цветная полоска, характеризующая дисперсию света в исследуемом материале.
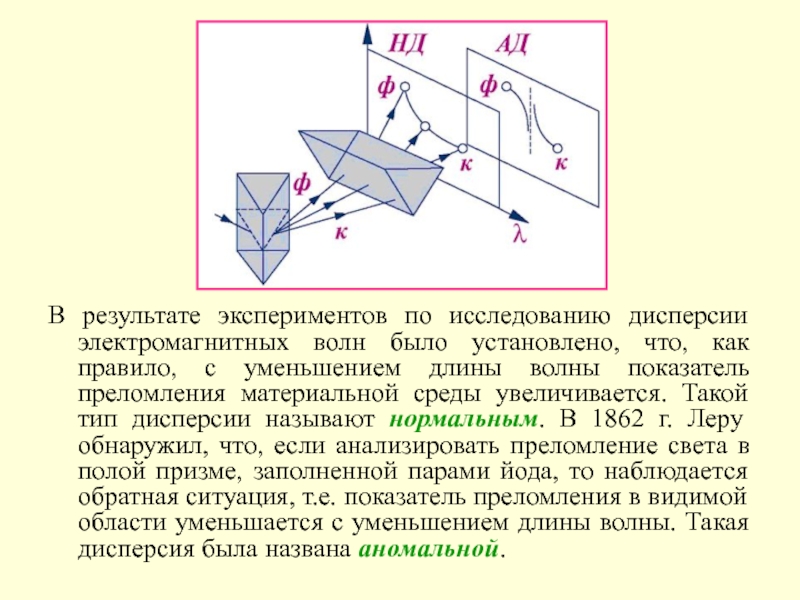
Слайд 5В результате экспериментов по исследованию дисперсии электромагнитных волн было установлено,
что, как правило, с уменьшением длины волны показатель преломления материальной
среды увеличивается. Такой тип дисперсии называют нормальным. В 1862 г. Леру обнаружил, что, если анализировать преломление света в полой призме, заполненной парами йода, то наблюдается обратная ситуация, т.е. показатель преломления в видимой области уменьшается с уменьшением длины волны. Такая дисперсия была названа аномальной.
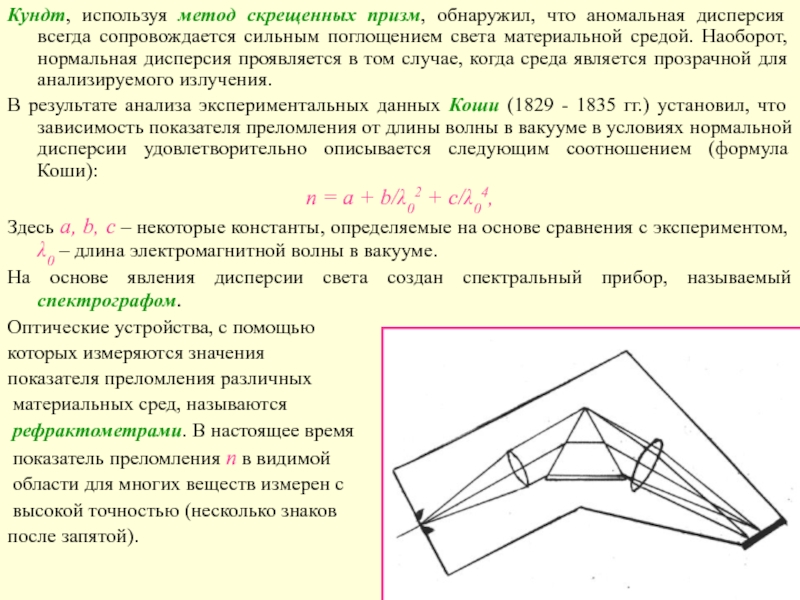
Слайд 6Кундт, используя метод скрещенных призм, обнаружил, что аномальная дисперсия всегда
сопровождается сильным поглощением света материальной средой. Наоборот, нормальная дисперсия проявляется
в том случае, когда среда является прозрачной для анализируемого излучения.
В результате анализа экспериментальных данных Коши (1829 - 1835 гг.) установил, что зависимость показателя преломления от длины волны в вакууме в условиях нормальной дисперсии удовлетворительно описывается следующим соотношением (формула Коши):
n = a + b/λ02 + c/λ04,
Здесь a, b, c – некоторые константы, определяемые на основе сравнения с экспериментом, λ0 – длина электромагнитной волны в вакууме.
На основе явления дисперсии света создан спектральный прибор, называемый спектрографом.
Оптические устройства, с помощью
которых измеряются значения
показателя преломления различных
материальных сред, называются
рефрактометрами. В настоящее время
показатель преломления n в видимой
области для многих веществ измерен с
высокой точностью (несколько знаков
после запятой).
Слайд 7Классическая теория
При проникновении электромагнитной волны в материальную среду происходит
формирование новой волны, распространяющейся по веществу. Отличие новой волны от
исходной состоит в том, что при ее распространении происходят процессы, связанные не только с колебаниями электрического и магнитного полей, но и с движением заряженных частиц внутри вещества, т.е. с возбуждениями чисто механической природы.
Согласно, модели Лоренца (Lorentz) предполагается, что внутри материальной среды имеются равномерно распределенные в пространстве заряженные частицы, колеблющиеся около своих положений равновесия лоренцевы осцилляторы. Простейший случай соответствует тому, что такими частицами являются электроны с массой m = 9,1х10-31 кг и зарядом |e| = 1,6x10-9 Кл. Для того чтобы среда была электрически нейтральна, необходимо допустить, что в ней присутствуют также частицы с положительным зарядом. Роль таких частиц могут играть относительно тяжелые ионы, движение которых на первом этапе можно не учитывать.
Схематически такую модель можно представить в виде кубической кристаллической решетки заряженных колеблющихся частиц. Одномерным аналогом такой решетки может служить кристаллическая цепочка частиц, не взаимодействующих друг с другом, но связанных упругими силами с тяжелыми ионами, расположенными в узлах кристаллической цепочки.

Слайд 8Если равновесные положения электронных осцилляторов несущественно изменяются в процессе электронных
колебаний, то модель Лоренца может быть использована для описания свойств
поляритонных волн не только в кристаллах, но и в других, менее упорядоченных средах: аморфных телах, стеклах, жидкостях и, с учетом некоторых ограничений, даже в разреженных средах. Модель Лоренца может быть использована также для описания свойств электромагнитных волн в твердых телах, содержащих равномерно распределенные в пространстве примесные центры.
Обозначим через u(l) вектор отклонения заряженной частицы (электрона) от положения равновесия. Здесь l = l1a1 + l2a2 + l3a3 – так называемый вектор трансляции, задающий положение элементарной ячейки в кубической кристаллической решетке; l1, l2, l3 – целые числа.
Запишем уравнение движения заряженной частицы с зарядом e(F)1/2 (F – так называемая сила осциллятора, характеризующая величину заряда колеблющейся частицы, e – заряд электрона; F ≈ 1) в поле электромагнитных волн с напряженностью E.
Слайд 9Решение системы уравнений для вещества и электромагнитного поля ищется в
виде плоских монохроматических волн.
Здесь ω = 2π/T = 2πf
– круговая частота, характеризующая колебания рассматриваемых величин в процессе распространения волны (f – обычная частота, измеряемая в герцах; k = (2π/λ)n – волновой вектор, направление которого задает направление распространения волны в пространстве; (λ – длина волны в материальной среде).
Получаем соотношение:
Относительная диэлектрическая проницаемость ε в общем случае предполагается зависящей от частот ω электромагнитной волны, т.е. ε = ε(ω).
Слайд 10где вводится обозначение:
для фазовой скорости поляритонной волны (электромагнитной волны
в среде).
При подстановке в уравнение решения в виде плоской монохроматической
волны
приходим к следующему алгебраическому соотношению:
Это соотношение в неявном виде задает так называемый закон дисперсии для поляритонной волны: ω = ω(k).
Слайд 11В дальнейшем удобно ввести обозначение для квадрата так называемой
плазменной
частоты ωp:
С использованием этого обозначения диэлектрическая функция представляется в виде:
или
где ωl2 = ω02 + ωp2 (ωl – значение частоты, при котором ε(ω) обращается в нуль).
Соответственно показатель преломления для рассматриваемой модели материальной среды представляется в виде:
Слайд 12Дисперсионные зависимости диэлектрической проницаемости ε(ν) и показателя преломления n(ν) для
кристалла фосфида галлия в инфракрасной области спектра .
Теперь мы можем
найти зависимость ω(k), т.е. закона дисперсии электромагнитных волн в материальной среде (поляритонных волн), исходя из соотношения
Используя выражение для диэлектрической проницаемости ε(ω), получаем:
Слайд 136.2. Нормальная и аномальная дисперсии.
Поглощение волн. Закон Бугера
В реальных
веществах колебания лоренцевых осцилляторов всегда являются затухающими. Это связано с
тем, что часть энергии в процессе колебаний лоренцева осциллятора переходит в тепло, т.е. в другие степени свободы материальной среды. Кроме того, трение возникает из-за самого процесса излучения (так называемое «радиационное трение»). Учет силы трения можно осуществить феноменологическим образом (не раскрывая механизма силы трения): путем введения в уравнение движения дополнительного слагаемого:
Слайд 15Поглощением (абсорбцией) света называется явление потери энергии световой волной, проходящей
через вещество.
Свет поглощается в тех случаях, когда проходящая волна затрачивает
энергию на различные процессы. Среди них: преобразование энергии волны во внутреннюю энергию – при нагревании вещества; затраты энергии на вторичное излучение в другом диапазоне частот (фотолюминесценция); затраты энергии на ионизацию – при фотохимических реакциях и т.п. При поглощении света колебания затухают и амплитуда электрической составляющей уменьшается по мере распространения волны. Для плоской волны, распространяющейся вдоль оси x, имеем
E(x) = E0exp(-αx) = E0exp(-βx).
Здесь E(x) – амплитудное значение напряженности электрического поля волны в точках с координатой x; E0 – амплитуда в точке с координатой x = 0; t – время, за которое волна распространилась на расстояние, равное x; β – коэффициент затухания колебаний; α = β/υф коэффициент поглощения, зависящий от химической природы среды и от длины волны проходящего света.
Интенсивность волны будет изменяться по закону Бугера (П. Бугер (1698 – 1758) – французский ученый):

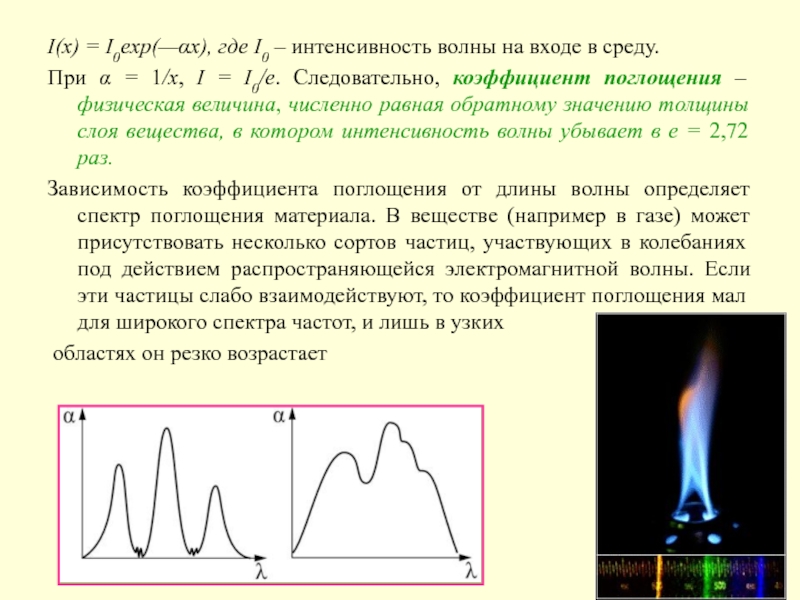
Слайд 16I(x) = I0exp(—αx), где I0 – интенсивность волны на входе
в среду.
При α = 1/x, I = I0/e. Следовательно, коэффициент
поглощения – физическая величина, численно равная обратному значению толщины слоя вещества, в котором интенсивность волны убывает в е = 2,72 раз.
Зависимость коэффициента поглощения от длины волны определяет спектр поглощения материала. В веществе (например в газе) может присутствовать несколько сортов частиц, участвующих в колебаниях под действием распространяющейся электромагнитной волны. Если эти частицы слабо взаимодействуют, то коэффициент поглощения мал для широкого спектра частот, и лишь в узких
областях он резко возрастает
Слайд 17Зависимостью коэффициента поглощения от частоты (длины волны) объясняется окрашенность поглощающих
тел. Например, стекло, слабо поглощающее красные и оранжевые лучи и
сильно поглощающее зеленые и синие, при освещении белым светом будет казаться красным. Если на такое стекло направить зеленый и синий свет, то из-за сильного поглощения света этих длин волн стекло будет казаться черным. Это явление используется для изготовления светофильтров, которые в зависимости от химического состава (стекла с присадками различных солей; пленки из пластмасс, содержащие красители; растворы красителей и т. д.) пропускают свет только определенных длин волн, поглощая остальные. Разнообразие пределов селективного (избирательного) поглощения у различных веществ объясняет разнообразие и богатство цветов и красок, наблюдающееся в окружающем мире.
Спектральный анализ позволяет получить информацию о составе Солнца, поскольку определенный набор спектральных линий исключительно точно характеризует химический элемент. Так, с помощью наблюдений спектра Солнца был открыт гелий.
Видимая часть солнечного излучения при изучении с помощью спектроанализирующих приборов оказывается неоднородной – в спектре наблюдаются линии поглощения, впервые описанные в 1814 году И. Фраунгофером.

Слайд 18Экстинкция (от лат. exstinctio — гашение), ослабление пучка света при
его распространении в веществе за счёт совместного действия поглощения света
и рассеяния света. В общем случае ослабление пучка с начальной интенсивностью I0 может быть рассчитано по закону Бугера—Ламберта—Бера.
I = I0exp(-bl),
где l — толщина поглощающего вещества, а b = α + r показатель экстинкции (показатель ослабления), равный сумме показателя поглощения α и рассеяния показателя r. Показатель экстинкции имеет размерность обратной длины (м-1, см-1). Безразмерный коэффициент экстинкции равен сумме поглощения коэффициента и рассеяния коэффициента среды. Как правило, показатели и коэффициенты экстинкции различны для разных длин волн света.
Слайд 196.3. Фазовая скорость. Волновой пакет. Групповая скорость
Фазовая скорость
E(r,t) =
E0expi(ωt-kr)
Условие постоянства фазы ωt – kr = const
Возьмем дифференциал
ωdt – kdr = 0 υ = dr/dt = ω/k – это есть скорость движения волнового фронта и называется волновой скоростью.
Множество точек в пространстве, в которых фаза волны имеет постоянное значение, называется волновым фронтом волны.
В вакууме при фазовая скорость распространения электромагнитной волны равна скорости света в вакууме.
В любой среде, где ε > 1, μ > 1 скорость распространения электромагнитной волны в n = (εμ)1/2 раз меньше, чем скорость света в вакууме.
Слайд 20Групповая скорость
Если волна представляет собой некоторое «возмущение» электромагнитного поля, например,
в виде импульса, равного нулю за пределами некоторого интервала Δr
и промежутка времени τ, то такое волновое поле называют волновым пакетом, если амплитуды гармонических волн, составляющих рассматриваемое возмущение, «заметно» отличаются от нуля лишь внутри некоторого интервала Δω вблизи средней частоты ω0. Если Δω/ω << 1, то волна называется почти гармонической или квазигармонической.
Имеет физический смысл оценка
скорости движения волнового
пакета или группы волн. Она
называется групповой скоростью υгр
Слайд 21Волновой пакет, или цуг волн:
Запишем фазу колебания как
Тогда:
A(r,t) медленно меняющаяся
амплитуда, представляющая собой огибающую цуга волн. Разложив зависимость [ω(k) –
ω0] в ряд и ограничившись первым членом разложения
Слайд 22Значит, что A(r,t) представляет собой суперпозицию низкочастотных составляющих, распространяющихся с
одинаковой скоростью
υ = dω/dk
С такой же скоростью движется волновой пакет
как целое.
В вакууме υфаз = υгр, т.к. частота и волновое число связаны линейным соотношением.
В любых других средах эта связь более сложная.
Учитывая что k = 2π/λ приходим к формуле Рэлея:
или
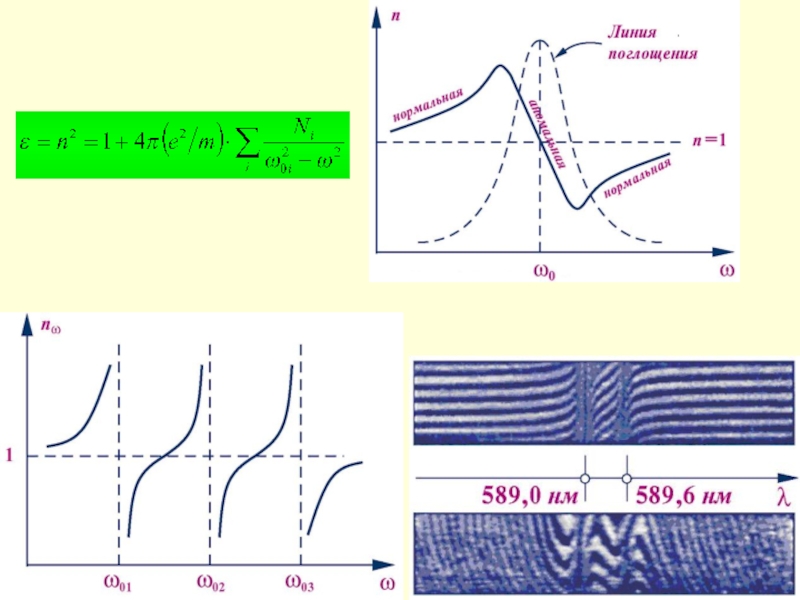
Слайд 23Возможны три случая:
; дисперсия отсутствует, практически только в вакууме,
в остальных средах равенство приближенное;
; показатель преломления убывает с ростом длины
волны; нормальная дисперсия → групповая скорость меньше фазовой; такой тип дисперсии характерен для прозрачных сред;
; показатель преломления растет с ростом длины
волны; аномальная дисперсия → групповая скорость больше фазовой и сильное поглощение.
Слайд 246.4. Рассеяние света. Прохождение света через оптически неоднородную среду. Рэлеевское
рассеяние.
Рассеяние Ми.
Рассеяние Мандельштама – Бриллюэна
Рассеяние света
Рассеяние света – это
изменение характеристик потока оптического излучения при его взаимодействии с веществом. Этими характеристиками могут быть пространственное распределение интенсивности, частотный спектр, поляризация света. Часто рассеяние света называется только обусловленное пространственной неоднородностью среды изменение направления распространения света, воспринимаемое как несобственное свечение среды.
С точки зрения волновой теории, падающая световая волна возбуждает в частицах среды вынужденные колебания электрических зарядов, которые становятся источниками вторичных световых волн. При этом определяющую роль играет интерференция света между падающей и вторичными волнами.
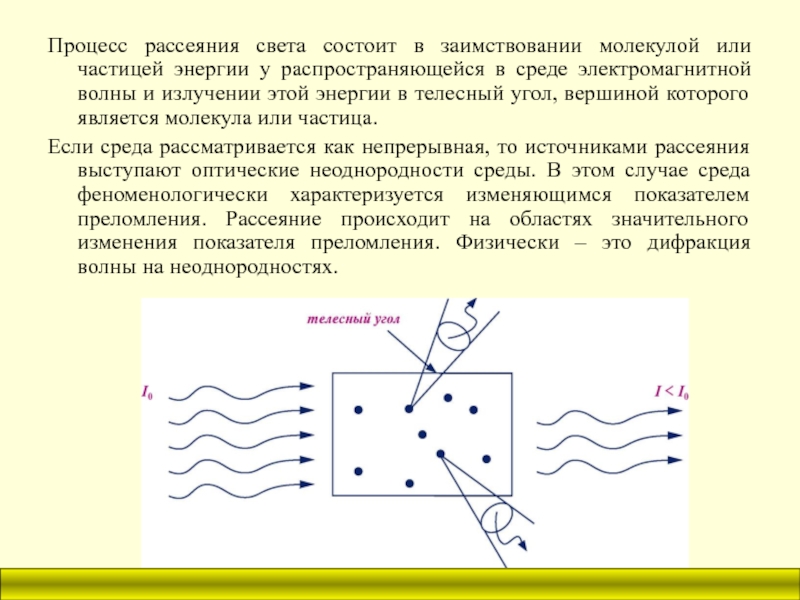
Слайд 25Процесс рассеяния света состоит в заимствовании молекулой или частицей энергии
у распространяющейся в среде электромагнитной волны и излучении этой энергии
в телесный угол, вершиной которого является молекула или частица.
Если среда рассматривается как непрерывная, то источниками рассеяния выступают оптические неоднородности среды. В этом случае среда феноменологически характеризуется изменяющимся показателем преломления. Рассеяние происходит на областях значительного изменения показателя преломления. Физически – это дифракция волны на неоднородностях.
Слайд 26Характер рассеяния зависит от соотношения между длиной волны и размером
частиц.
1. Если линейные размеры частиц меньше, чем , то рассеяние
называется рэлеевским (Д.У. Рэлей (1842-1919)).
2. При больших размерах частиц принято говорить о рассеянии Ми (рассеивание на сферических частицах).
Неоднородность оптических свойств среды при распространение в ней звуковой волны приводит к гармоническим изменениям оптических свойств среды во времени. В результате возникает дифракция света при распространение его в среде. Этот вид рассеяния получил название явление Мандельштама-Бриллюэна.
Многократное рассеяние.
Рассеянное частицей излучение в свою очередь может быть рассеянно другой частицей и так далее. Каждое такое рассеяние идет по законам однократного рассеяния. Окончательный результат – суммирование однократных рассеяний с учетом статистических характеристик их следования друг за другом.
Слайд 27Рэлеевское рассеяние
Количественной характеристикой рассеяние света является дифференциальное сечение рассеяния dσ,
определяемое как отношение потока излучения dI, рассеянного в малый элемент
телесного угла dΩ, к величине падающего потока I0: dσ = dI/I0. Полное сечение рассеяния σ есть сумма dσ по всем dΩ (сечение измеряют обычно в см2). При упругом рассеянии можно считать, что σ — размер площадки, «не пропускающей свет» в направлении его первоначального распространения. При классическом описании рассеяние света часто пользуются матрицей рассеяния, связывающей амплитуды падающей и рассеянных по всевозможным направлениям световых волн и позволяющей учесть изменение состояния поляризации рассеянного света.
Неполной, но наглядной характеристикой
рассеяние света служит
индикатриса рассеяния — кривая,
графически отображающая различие в
интенсивностях света, рассеянного в разных
направлениях (полярная диаграмма).
Слайд 28Рэлеевское рассеяние — рассеяние света без изменения длины волны (называемое
также упругим рассеянием) на частицах, неоднородностях или других объектах, когда
частота рассеиваемого света существенно меньше собственной частоты рассеивающего объекта или системы. Иначе говоря это рассеяние света на объектах, размеры которых меньше его длины волны.
Для рассеивания на осцилляторе массы m, с зарядом q и собственной частотой ν0 сечение рассеяния σR пропорционально четвёртой степени частоты рассеиваемого света ν:
Эту зависимость вывел британский физик Дж. Рэлей в 1871 г.
Сечение σR зависит от угла рассеяния θ между направлениями падающей и рассеянной волн:
Рэлеевским рассеянием солнечного света на неоднородностях атмосферы (флуктуационные неоднородности плотности воздуха) объясняется голубой цвет неба и краски заката Солнца (селективное рассеяние).
Слайд 29Рассеяние Ми
Рассеяние на частицах размеры, которых относятся к рассеянию Ми.
Теория рассеяния Ми учитывает размеры частиц и выражает рассеяние в
виде ряда, малым параметром в котором служит:
ρ = ka = 2πa/λ,
где – радиус сферической частицы. Термин «рассеяние Ми» употребляется также и для рассеяния на частицах других форм.
Амплитуда, фаза и поляризация вторичной волны являются сложными функциями двух параметров ρ = ka (а - радиус частицы, k - волновое число) и комплексного показателя преломления n = n′ —iκ (n′ – вещественный показатель преломления, κ – показатель поглощения). Вторичные волны называются парциальными волнами Mи. Полная интенсивность рассеянного света определяется суммой бесконечного числа парциальных волн.
При ka << 1 и |n|ka << 1 сферу можно рассматривать как электрический диполь, и теория Mи приводит к формуле Рэлея. Если ka << 1, но |n|ka не мало, то при значениях |n|ka = mπ, где т - целое число, сечение рассеяния резко возрастает (резонансы Ми).
Слайд 30При увеличении размеров частицы интенсивность последующих парциальных электромагнитных волн возрастает.
Для больших частиц (ka > 1) число учитываемых парциальных волн
~ ka.
С ростом ka индикатриса приобретает многолепестковую форму, вытягиваясь вперёд. В дифрагированном пучке наблюдается система постоянно убывающих тёмных и светлых колец, т. н. венцы. Обычно в реальной дисперсной системе вместо венцов в области малых углов происходит постепенное уменьшение интенсивности рассеяния. Рассеяние вперёд усиливается, назад — ослабевает; зависимость поляризации света от угла рассеяния значительно усложняется. Это явление известно под названием эффекта Ми. По распределение интенсивности можно восстановить функцию распределения частиц по размерам. Основанный на этой идее метод малых углов используется в разнообразных технологических и геофизических задачах.
Теория Mи обобщена и на неоднородные сферы, на эллипсоиды вращения и трёхмерные эллипсоиды, на системы частиц случайной формы и ориентации. Точного решения задач дифракции на таких частицах нет, но разработано много приближённых методов расчёта.
Слайд 31Чем больше рассеяние на аэрозолях, тем более белесоватый оттенок принимает
цвет неба. Рассеяние на аэрозолях также уменьшает долю рассеянной радиации,
направленной в мировое пространство; интенсивность рассеянной радиации, направленной к земле, возрастает.
Имеет значение не абсолютный размер частицы, а соотношение размера частицы и длины волны. При увеличении размеров частиц в рассеянии Ми проявляется преимущественно рассеяние вперед.
Важной особенностью рассеяния Ми является его слабая зависимость от длины волны для частиц, линейные размеры которых много больше длины волны, что существенно отличается от рассеяния Рэлея. Благодаря этому, облака являются белыми, а небо голубым. Заметим, что при увеличении размеров частиц индикатриса рассеяния вытягивается в направлении вперед, что происходит, например, в дождевых облаках, когда капельки воды становятся достаточно крупными и готовы упасть в виде дождя. При этом отраженная компонента значительно уступает компоненте с малыми углами рассеяния, т.е. частицы в основном пропускают
световое излучение в направлении вперед
(становятся прозрачными), мы зрительно
воспринимаем такие облака как темные
дождевые.

Слайд 32Рассеяние Мандельштама – Бриллюэна
Л. И. Мандельштам показал (1907), что принципиально
необходимым для рассеяние света в сплошной среде является нарушение её
оптической однородности, при котором показатель преломления среды не постоянен, а меняется от точки к точке. В безграничной и полностью однородной среде волны, упруго рассеянные отдельными частицами по всем направлениям, не совпадающим с направлением первичной волны, взаимно «гасятся» в результате интерференции. Оптическими неоднородностями (кроме границ среды) являются включения инородных частиц, а при их отсутствии — флуктуации плотности, анизотропии и концентрации, которые возникают в силу статистической природы теплового движения частиц.
В жидкостях, в отличие от газов, движение частиц более сложное, и в нём выражен коллективный характер. Это определяет особенности временной эволюции флуктуации и проявляется в спектрах неупругого (т. н. квазиупругого) рассеяние света в жидкостях. Наиболее интенсивно рассеяния света происходит на больших флуктуациях, затухание которых мало, например, на упругих волнах, вызывающих соответствующую неоднородность показателя преломления (рассеяние Мандельштама - Бриллюэна).

Слайд 33Это процесс неупругий, происходящий с изменением частоты света: в результате
рассеяния монохроматического излучения получается спектр, состоящий из несмещённой рэлеевской линии
и дублета линий-сателлитов, симметрично удалённых от рэлеевской на величину Δω, зависящую от скорости u упругой волны и угла рассеяния θ:
Δω = ω – ω′ = ±2ω(v/c)sin(θ/2).
В спектрах рассеяние света в жидкостях выделяют близкую к рэлеевской линии область (Δω/с < 1 см-1) тонкой структуры, область крыла рэлеевской линии (до 100 – 150 см-1) и далёкую область, спектр которой определяется внутримолекулярными движениями.
Спектры рассеяния Мандельштама - Бриллюэна (тонкая структура рэлеевской линии) в СС14 для разных углов рассеяния.
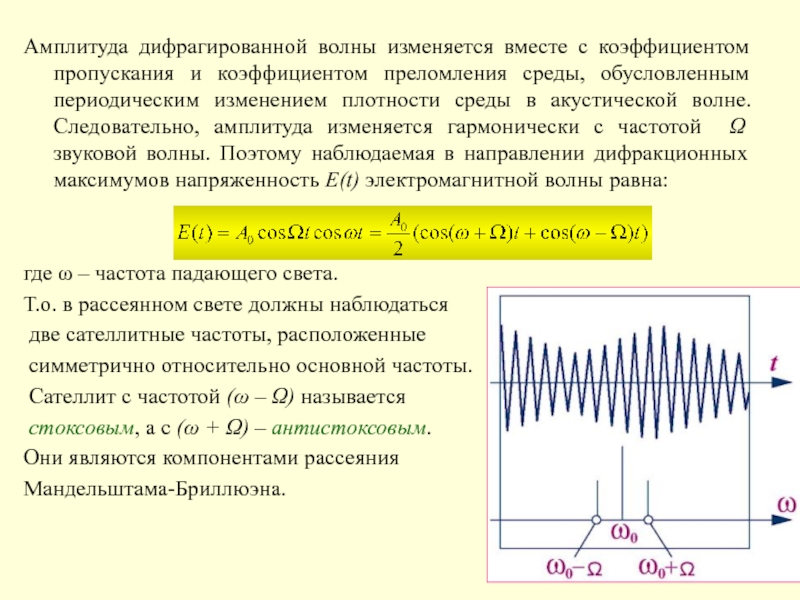
Слайд 34Амплитуда дифрагированной волны изменяется вместе с коэффициентом пропускания и коэффициентом
преломления среды, обусловленным периодическим изменением плотности среды в акустической волне.
Следовательно, амплитуда изменяется гармонически с частотой Ω звуковой волны. Поэтому наблюдаемая в направлении дифракционных максимумов напряженность E(t) электромагнитной волны равна:
где ω – частота падающего света.
Т.о. в рассеянном свете должны наблюдаться
две сателлитные частоты, расположенные
симметрично относительно основной частоты.
Сателлит с частотой (ω – Ω) называется
стоксовым, а с (ω + Ω) – антистоксовым.
Они являются компонентами рассеяния
Мандельштама-Бриллюэна.
Слайд 35Явление рассеяние света чрезвычайно широко используется при самых разнообразных исследованиях
в физике, химии, в различных областях техники. Спектры рассеяние света
позволяют определять молекулярные и атомные характеристики веществ, их упругие, релаксационные и др. постоянные. В ряде случаев эти спектры являются единственным источником информации о запрещенных переходах в молекулах. На рассеяние света основаны многие методы определения размеров, а иногда и формы мелких частиц, что особенно важно, например, при измерении видимости атмосферной и при исследовании полимерных растворов. Процессы вынужденного рассеяние света лежат в основе т. н. активной спектроскопии и широко используются в лазерах с перестраиваемой частотой.