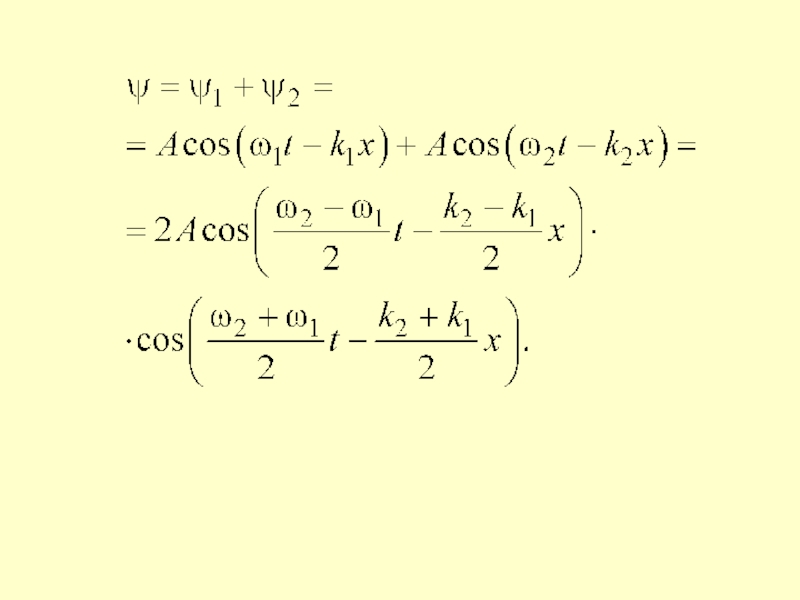Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Раздел курса Колебания и волны
Содержание
- 1. Раздел курса Колебания и волны
- 2. Бесконечная монохроматическая волна, уравнение которой имеет вид не может быть использована для передачи информации.
- 3. Для того, чтобы волна могла
- 4. Рассмотрим волну с амплитудной модуляцией. Для
- 5. Ранее было показано, что биения
- 6. Обе волны возбуждают одинаково направленные
- 7. Слайд 7
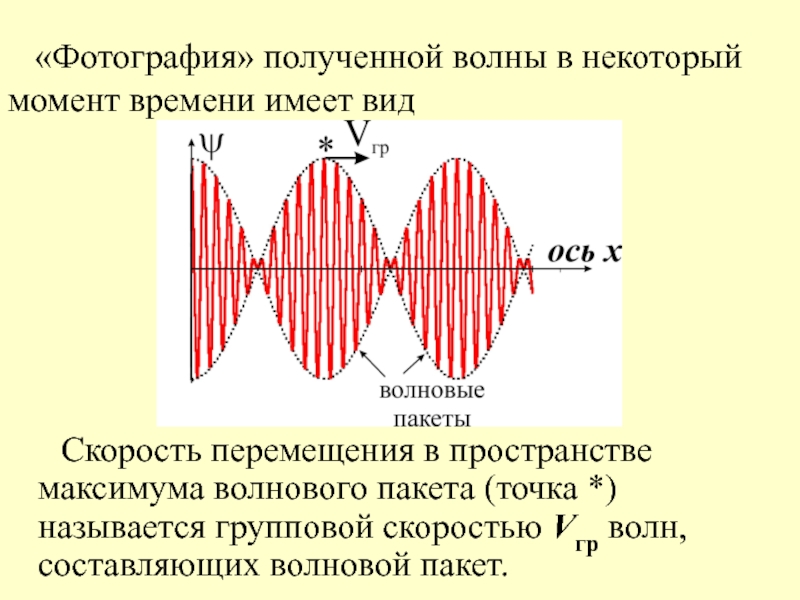
- 8. «Фотография» полученной волны в некоторый
- 9. Огибающая волнового пакета определяется в уравнении модулированной волны членом
- 10. В процессе перемещения такой модулированной
- 11. Поставим задачу: выразить групповую
- 12. Итак, показано, что групповая скорость волн равна
- 13. Итак, показано, что групповая скорость волны выражается через фазовую скорость формулой
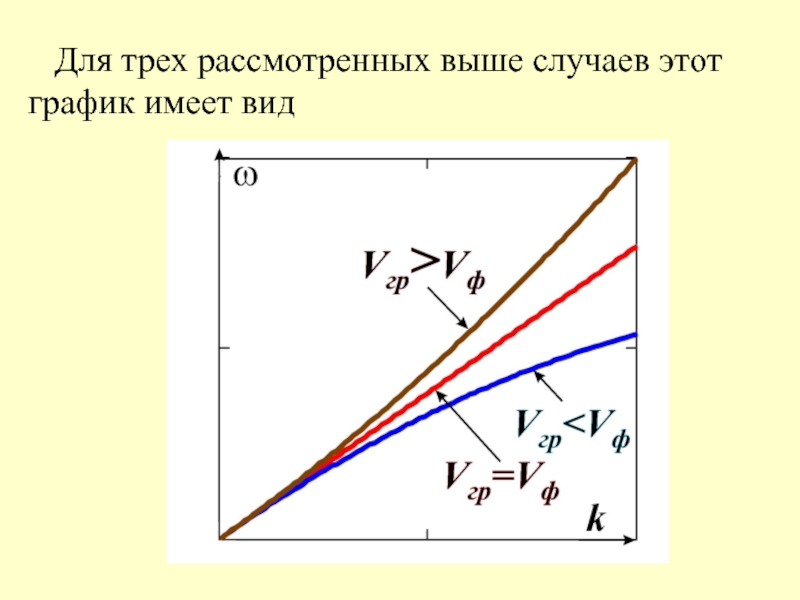
- 14. Рассмотрим три случая: 1) Vф
- 15. 2) Vф растет с ростом длины волны , то есть(наблюдается нормальная дисперсия);
- 16. 3) Vф уменьшается с ростом длины волны , то есть(наблюдается аномальная дисперсия).
- 17. Итак, если дисперсия отсутствует, то групповая скорость
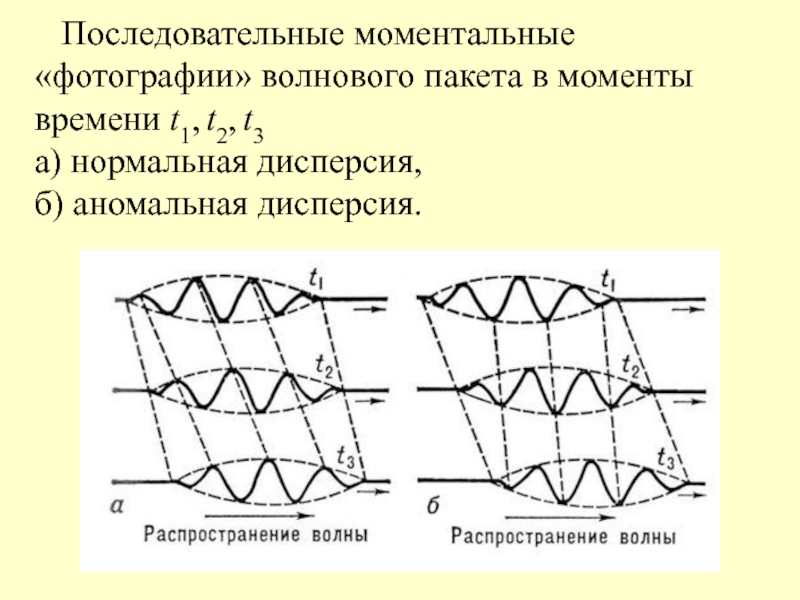
- 18. Последовательные моментальные «фотографии» волнового пакета
- 19. График зависимости циклической частоты волны от волнового числа =f(k) называется дисперсионным.
- 20. Для трех рассмотренных выше случаев этот график имеет вид
- 21. Скачать презентанцию
Бесконечная монохроматическая волна, уравнение которой имеет вид не может быть использована для передачи информации.
Слайды и текст этой презентации
Слайд 2 Бесконечная монохроматическая волна, уравнение которой имеет вид
не может быть
использована для передачи информации.
Слайд 3 Для того, чтобы волна могла переносить информацию, необходимо
изменять со временем (модулировать) её параметры А, или .
Соответственно существуют амплитудная, частотная и фазовая модуляции волны.
Слайд 4 Рассмотрим волну с амплитудной модуляцией.
Для того, чтобы создавать
волну, амплитуда которой изменяется со временем, источник волны должен совершать
колебания то с большей, то с меньшей амплитудой, то есть в простейшем случае совершать биения.
Слайд 5 Ранее было показано, что биения возникают при сложении
двух однонаправленных гармонических колебаний, частоты которых 1 и 2 различны,
но мало отличаются друг от друга:Следовательно, источник, который совершает биения, создает две гармонические волны, бегущие в одном направлении, частоты которых 1 и 2.
Слайд 6 Обе волны возбуждают одинаково направленные колебания в одних
и тех же точках пространства. Получим уравнение результирующей волны
считая, что биения источника происходят при сложении гармонических косинусоидальных колебаний с нулевой начальной фазой и одинаковыми амплитудами.
Слайд 8 «Фотография» полученной волны в некоторый момент времени имеет
вид
Скорость перемещения в пространстве максимума волнового пакета
(точка *) называется групповой скоростью Vгр волн, составляющих волновой пакет.
Слайд 10 В процессе перемещения такой модулированной волны для точки,
обозначенной звездочкой (*), постоянной остается фаза, стоящая в этом выражении:
Здесь
x* - координата максимума волнового пакета.
Слайд 11 Поставим задачу: выразить групповую скорость Vгр через
циклические частоты 1, 2 и волновые числа k1, k2 волн,
составляющих волновой пакет.
Слайд 12Итак, показано, что групповая скорость волн равна производной от циклической
частоты по волновому числу:
Поставим задачу: найти связь групповой
и фазовой скорости волны:
Слайд 14Рассмотрим три случая:
1) Vф f() – фазовая
скорость не зависит от длины волны (явление дисперсии волн отсутствует);
Слайд 17 Итак,
если дисперсия отсутствует, то групповая скорость волн равна фазовой
если
наблюдается нормальная дисперсия, то групповая скорость волн меньше фазовой
если наблюдается
аномальная дисперсия, то групповая скорость волн больше фазовой
Слайд 18 Последовательные моментальные «фотографии» волнового пакета в моменты времени
t1, t2, t3
а) нормальная дисперсия,
б) аномальная дисперсия.
Слайд 19 График зависимости циклической частоты волны от волнового числа
=f(k) называется дисперсионным.
