Развертка усеченной поверхности

Содержание

1. Развертка усеченной поверхности
2. Слайд 2
3. Алгоритм решения:Основание пирамиды принадлежит плоскости проекций П1,
4. 2. Т.к. плоскость α занимает общее положение,
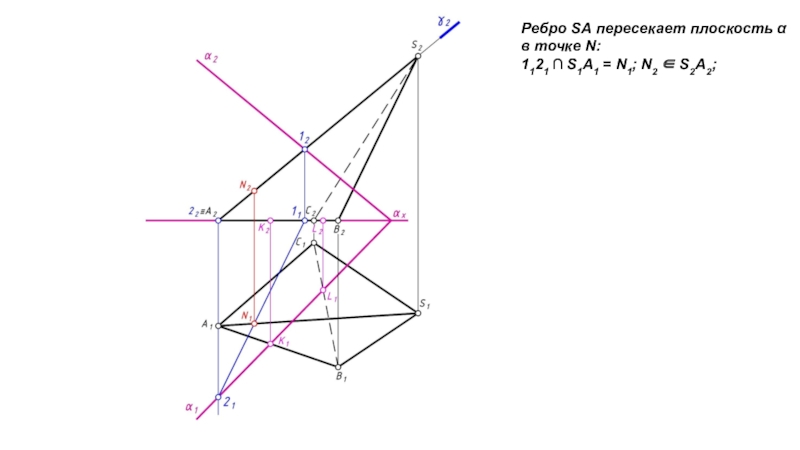
5. Ребро SА пересекает плоскость α в точке N:1121  S1А1 = N1; N2  S2А2;
6. Заключим ребро SC в горизонтально-проецирующую плоскость .
7. Ребро SС пересекает плоскость α в точке
8. КLPN – искомая линия пересечения.Ее видимость определяем по видимости граней, которым она принадлежит.
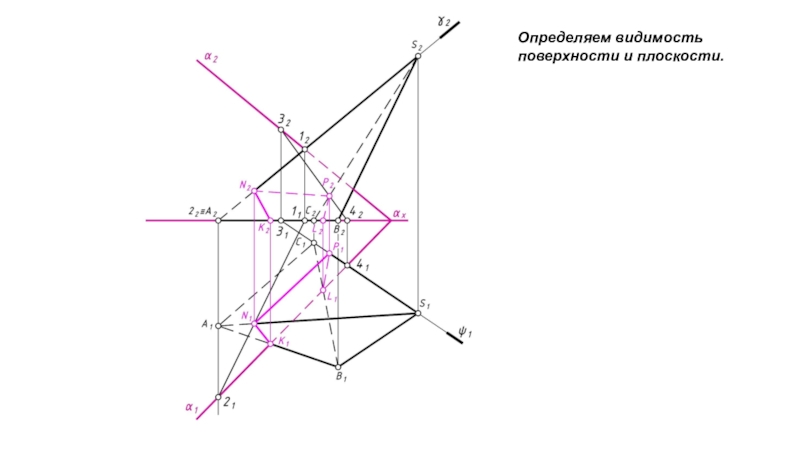
9. Определяем видимость поверхности и плоскости.
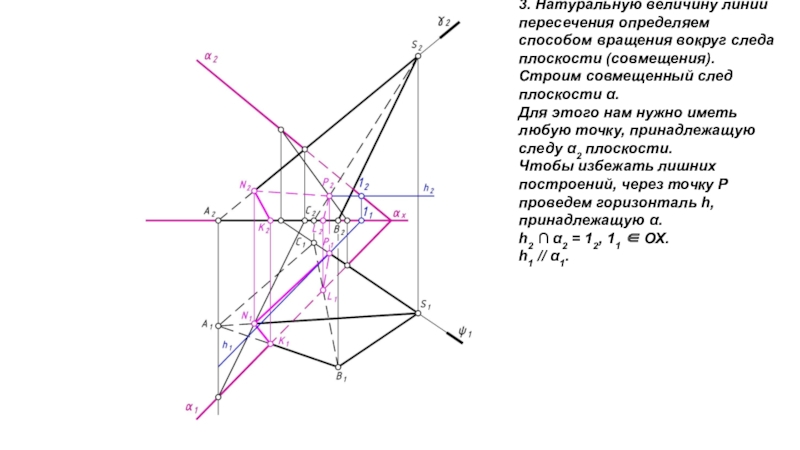
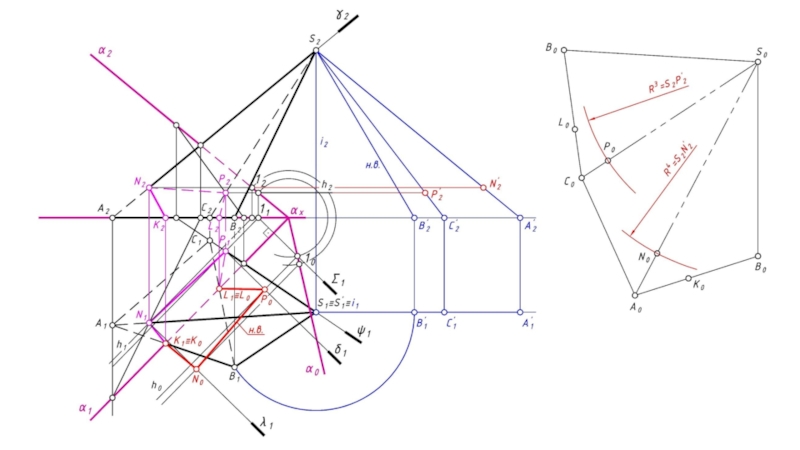
10. 3. Натуральную величину линии пересечения определяем способом
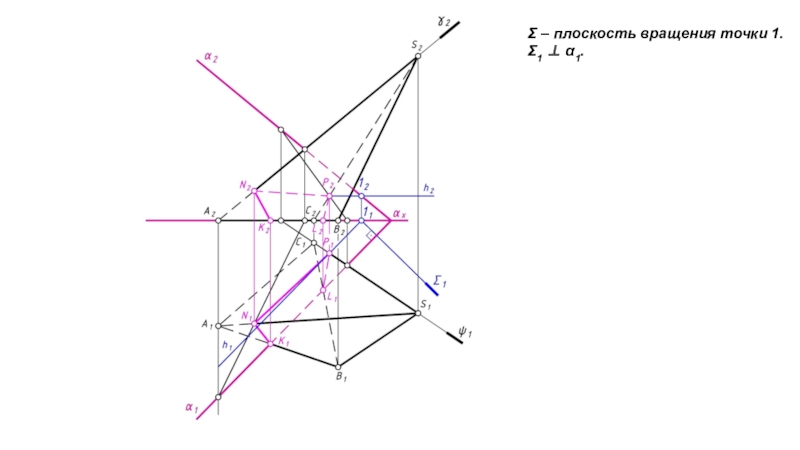
11. Σ – плоскость вращения точки 1. Σ1  α1.
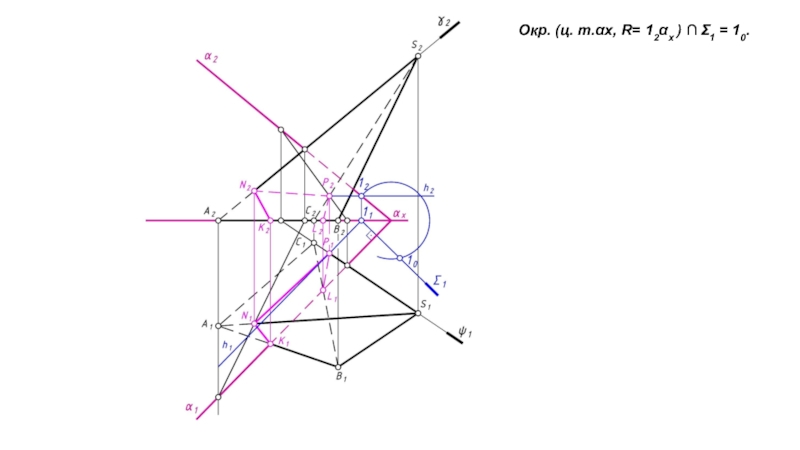
12. Окр. (ц. т.αх, R= 12αх )  Σ1 = 10.
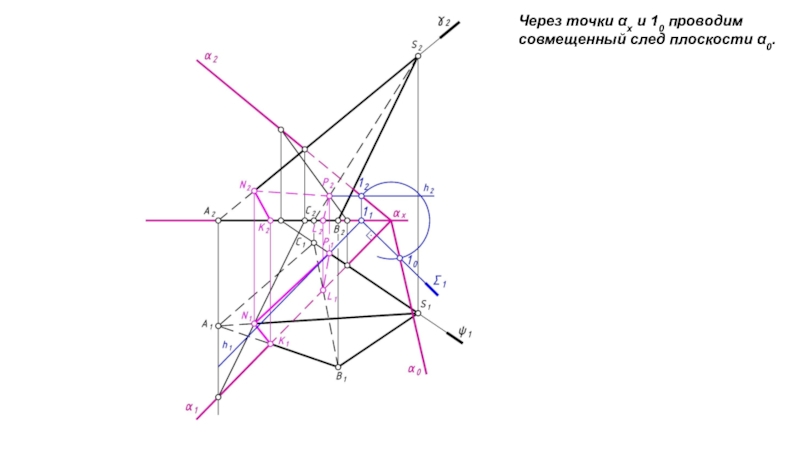
13. Через точки αх и 10 проводим совмещенный след плоскости α0.
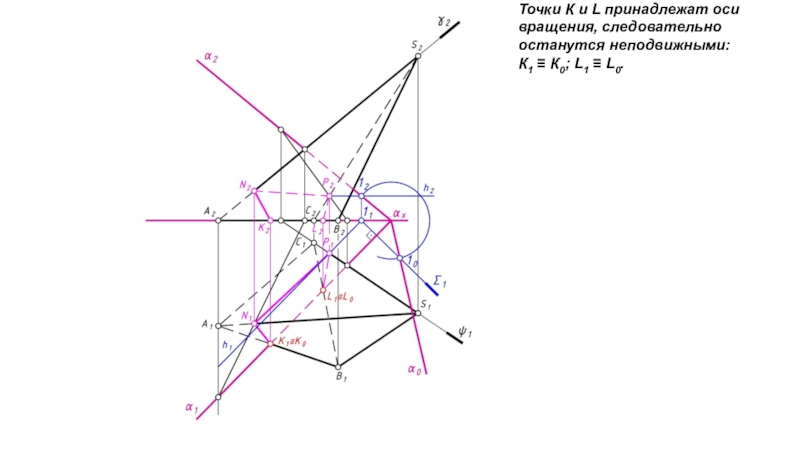
14. Точки К и L принадлежат оси вращения, следовательно останутся неподвижными:К1  К0; L1  L0.
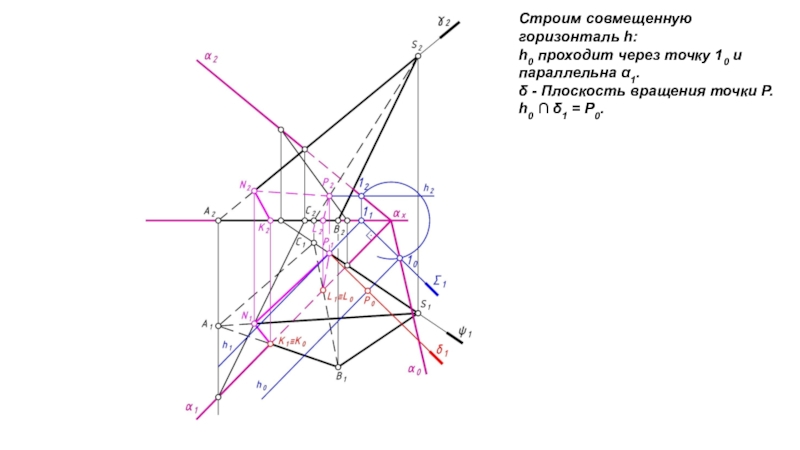
15. Строим совмещенную горизонталь h:h0 проходит через точку
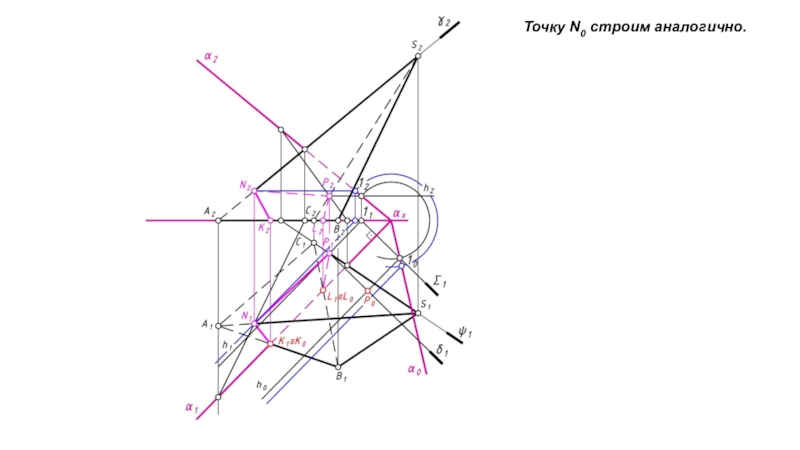
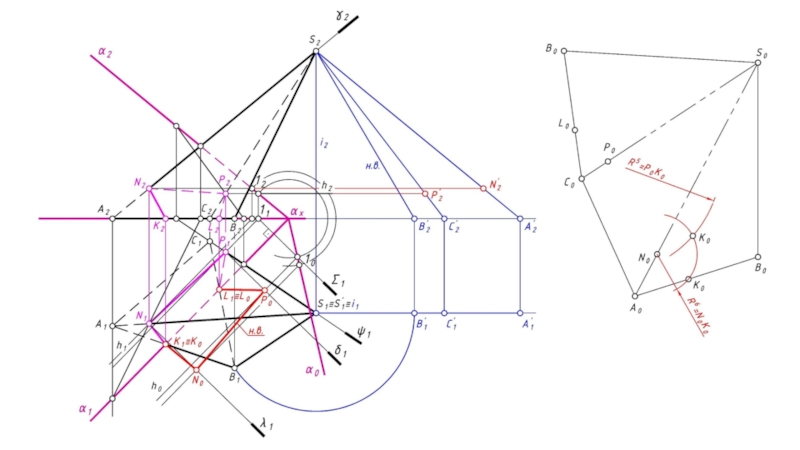
16. Точку N0 строим аналогично.
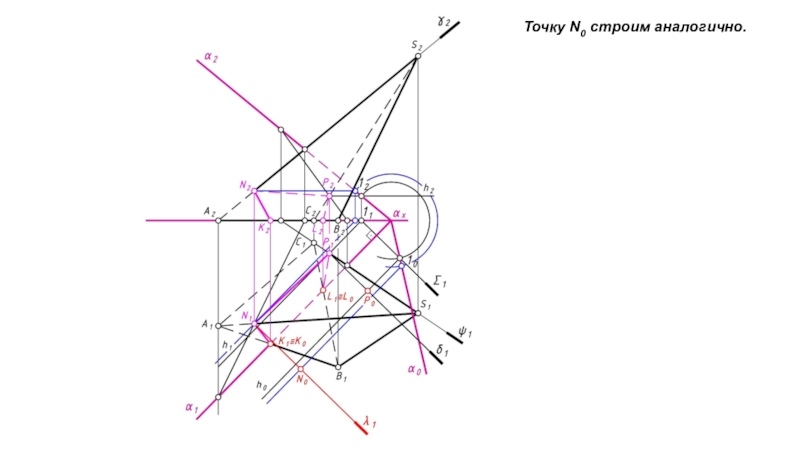
17. Точку N0 строим аналогично.
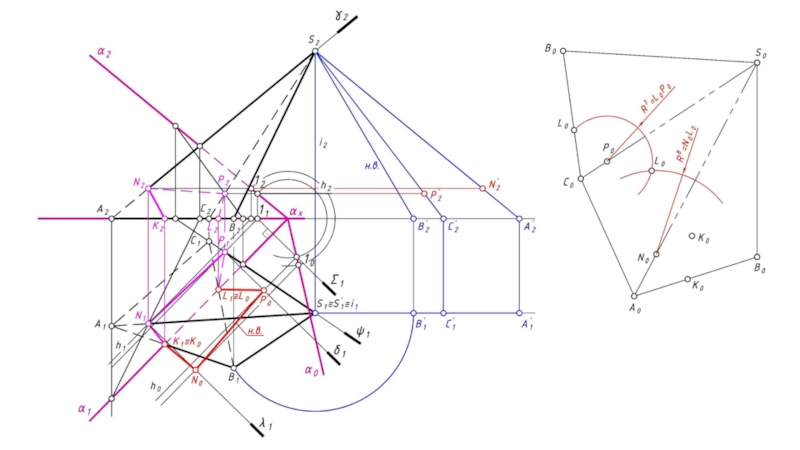
18. К0L0P0N0 – н.в. KLPN.
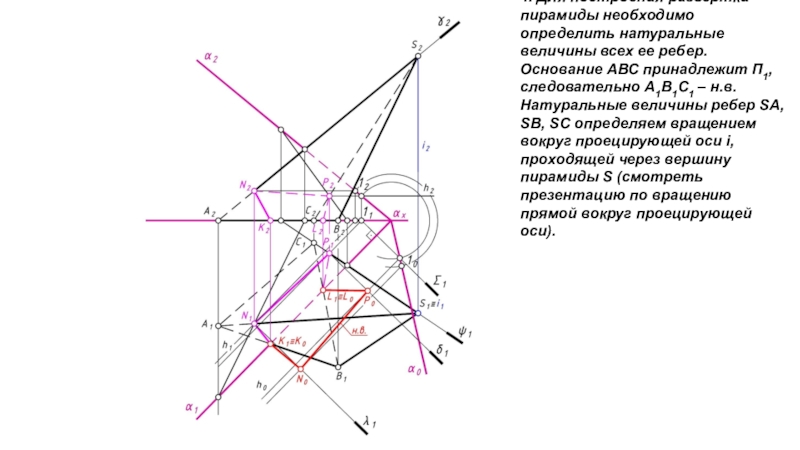
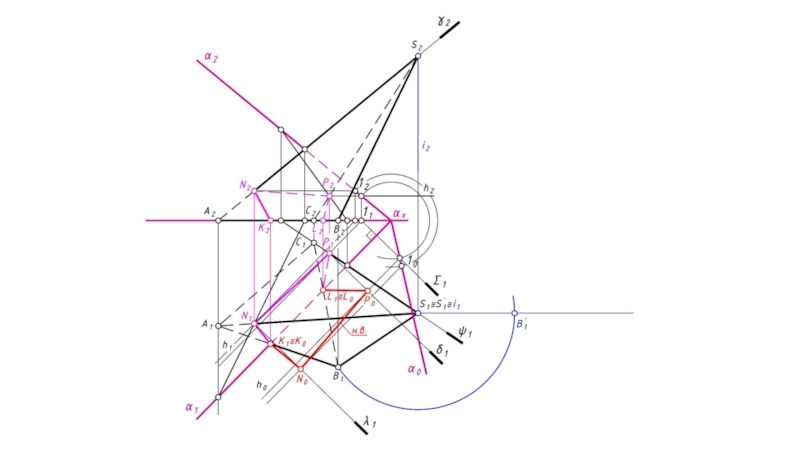
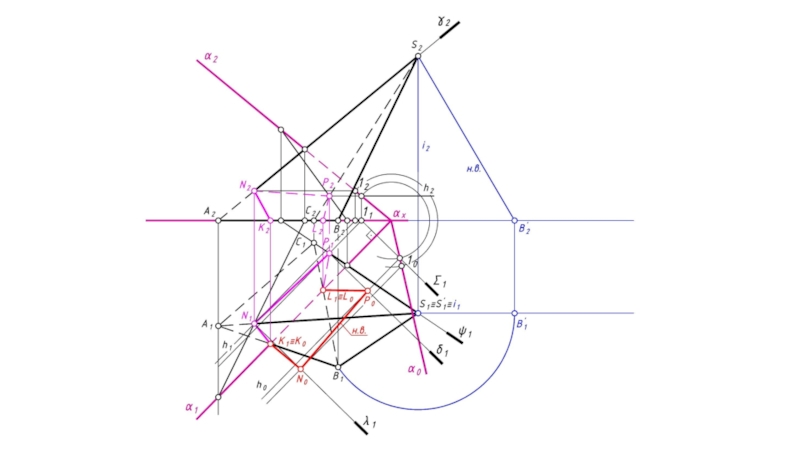
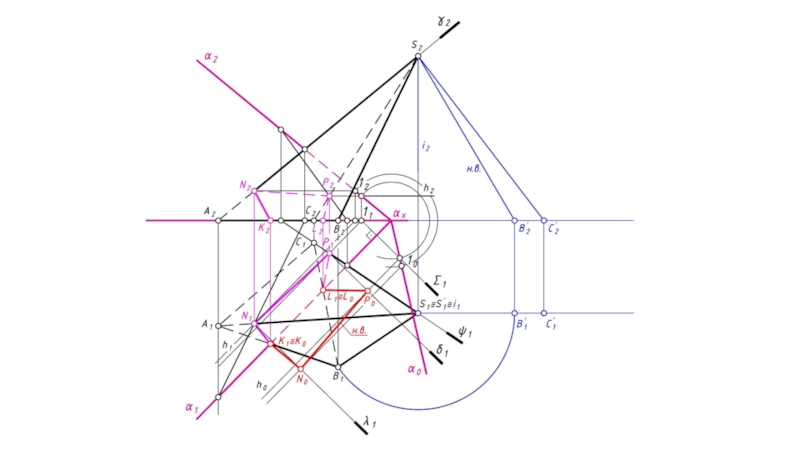
19. 4. Для построения развертки пирамиды необходимо определить
20. Слайд 20
21. Слайд 21
22. Слайд 22
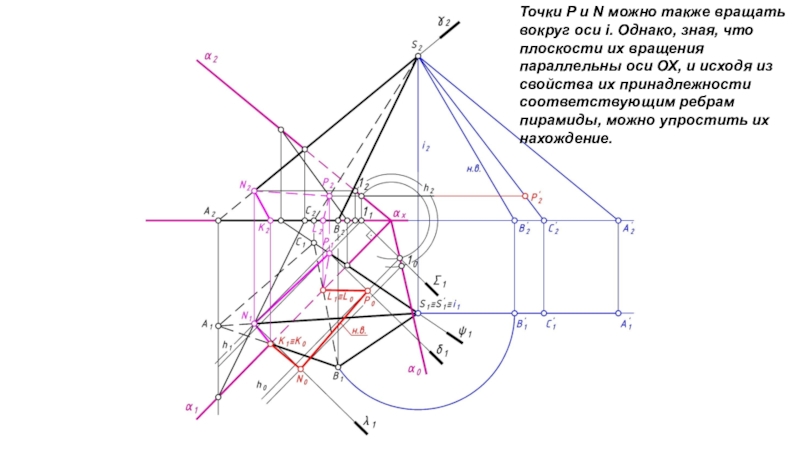
23. Точки P и N можно также вращать
24. Слайд 24
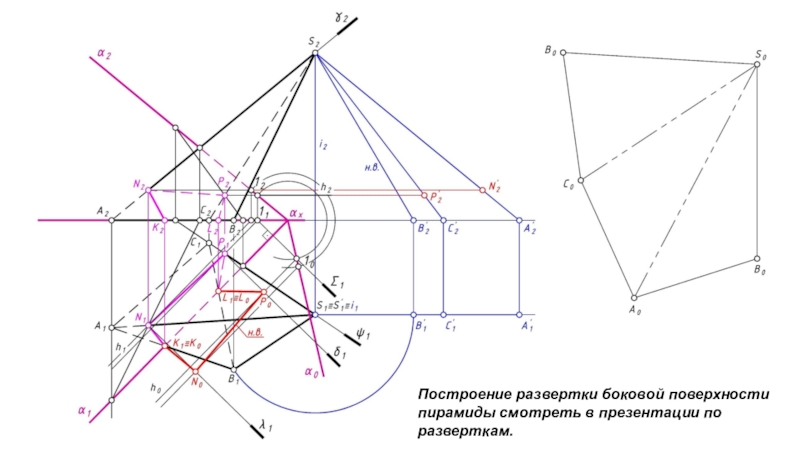
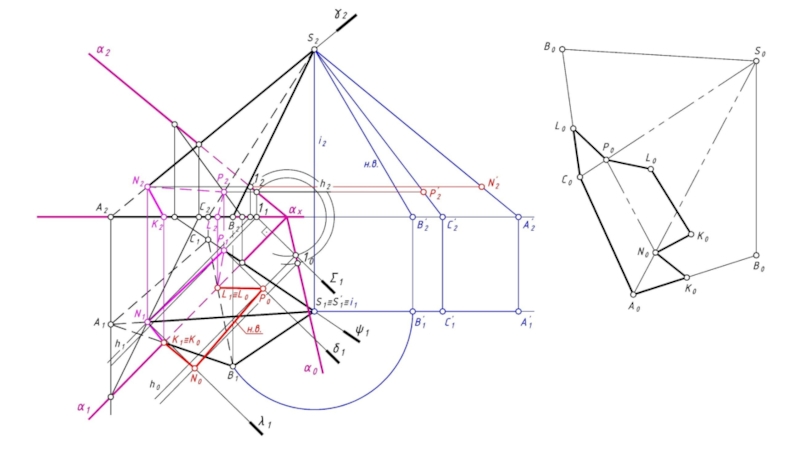
25. Построение развертки боковой поверхности пирамиды смотреть в презентации по разверткам.
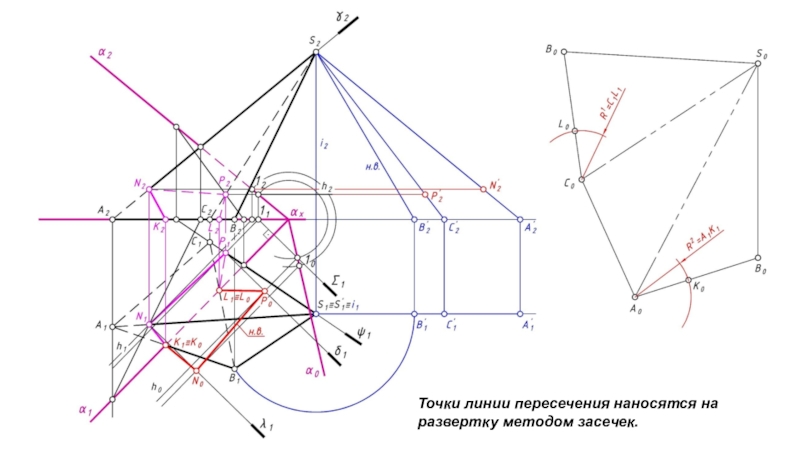
26. Точки линии пересечения наносятся на развертку методом засечек.
27. Слайд 27
28. Слайд 28
29. Слайд 29
30. Слайд 30
31. Скачать презентанцию

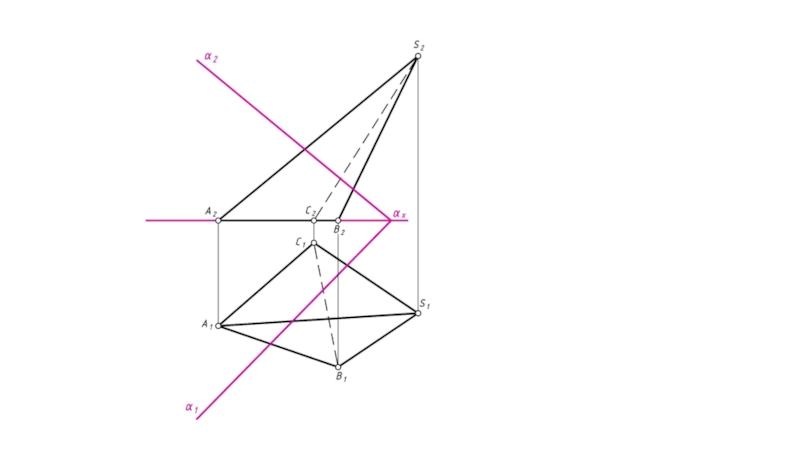
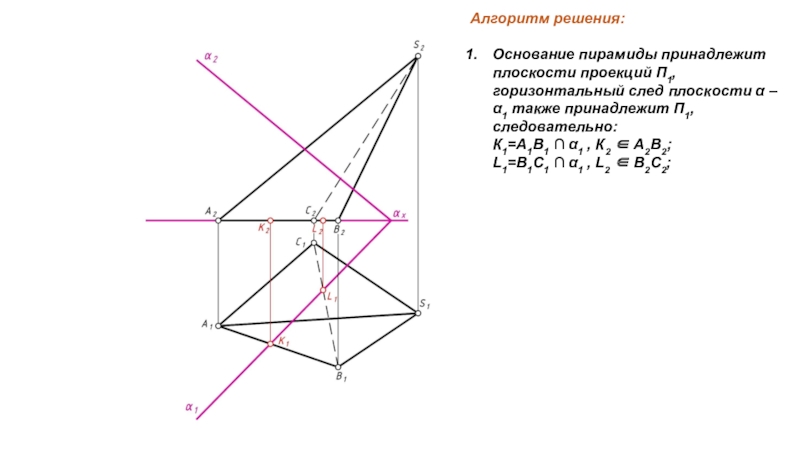
Алгоритм решения:Основание пирамиды принадлежит плоскости проекций П1, горизонтальный след плоскости α – α1 также принадлежит П1, следовательно: К1=А1В1  α1 , К2  А2В2; L1=В1С1  α1 , L2  В2С2;

Главная
Разное
Развертка усеченной поверхности

Слайды и текст этой презентации

Слайд 1Развертка усеченной поверхности

Слайд 2

Слайд 3Алгоритм решения:

Основание пирамиды принадлежит плоскости проекций П1, горизонтальный след плоскости

α – α1 также принадлежит П1, следовательно: К1=А1В1  α1 ,

К2  А2В2; L1=В1С1  α1 , L2  В2С2;

Алгоритм решения:Основание пирамиды принадлежит плоскости проекций П1, горизонтальный след плоскости α – α1 также принадлежит П1, следовательно:

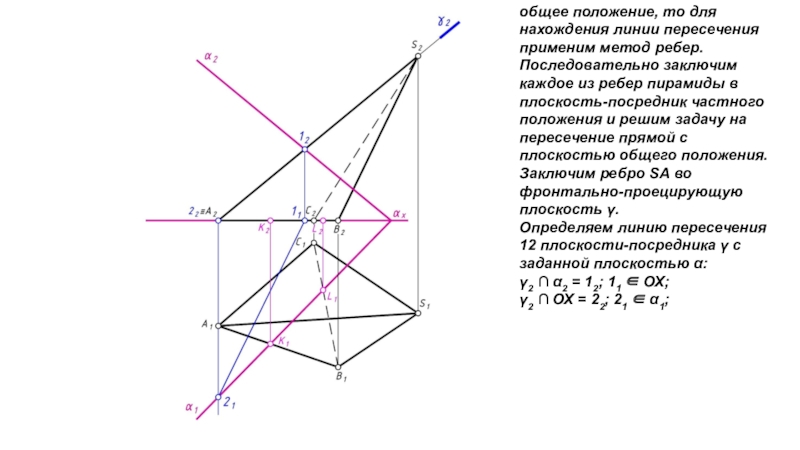
Слайд 42. Т.к. плоскость α занимает общее положение, то для нахождения

линии пересечения применим метод ребер. Последовательно заключим каждое из ребер

пирамиды в плоскость-посредник частного положения и решим задачу на пересечение прямой с плоскостью общего положения. Заключим ребро SА во фронтально-проецирующую плоскость . Определяем линию пересечения 12 плоскости-посредника  с заданной плоскостью α: 2  α2 = 12; 11  ОХ;
2  ОХ = 22; 21  α1;

2. Т.к. плоскость α занимает общее положение, то для нахождения линии пересечения применим метод ребер. Последовательно заключим

Слайд 5Ребро SА пересекает плоскость α в точке N:
1121  S1А1

= N1; N2  S2А2;

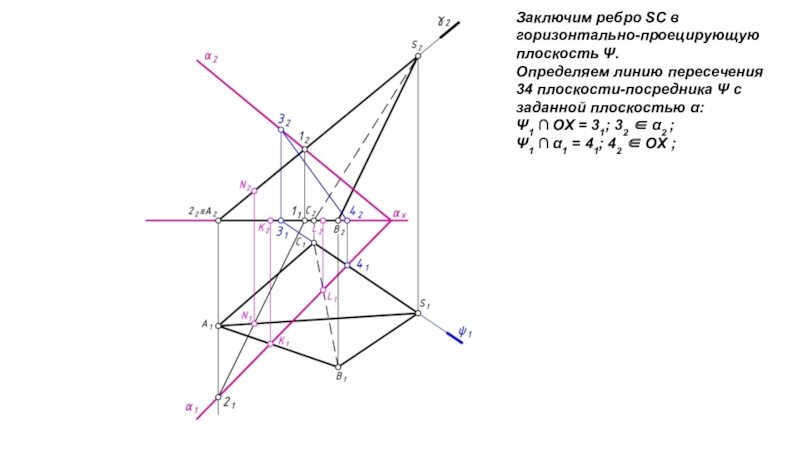
Слайд 6Заключим ребро SC в горизонтально-проецирующую плоскость . Определяем линию пересечения 34

плоскости-посредника  с заданной плоскостью α: 1  ОХ = 31;

32  α2 ;
1  α1 = 41; 42  ОХ ;

Заключим ребро SC в горизонтально-проецирующую плоскость . Определяем линию пересечения 34 плоскости-посредника  с заданной плоскостью α:

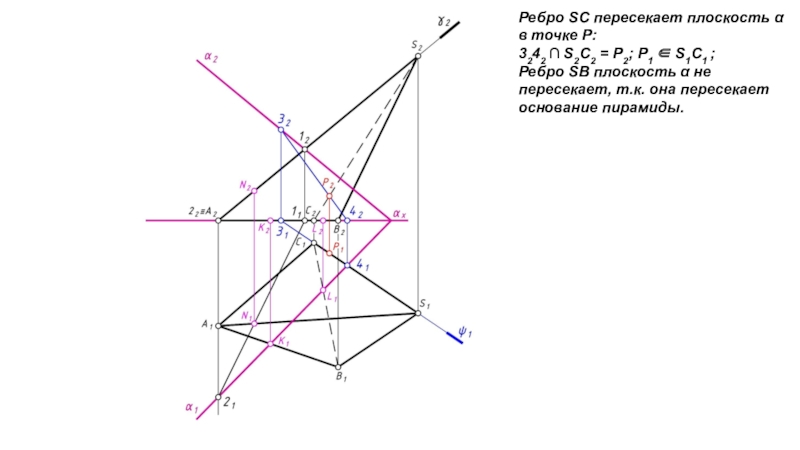
Слайд 7Ребро SС пересекает плоскость α в точке Р:
3242  S2С2

= Р2; Р1  S1С1 ;
Ребро SB плоскость α не

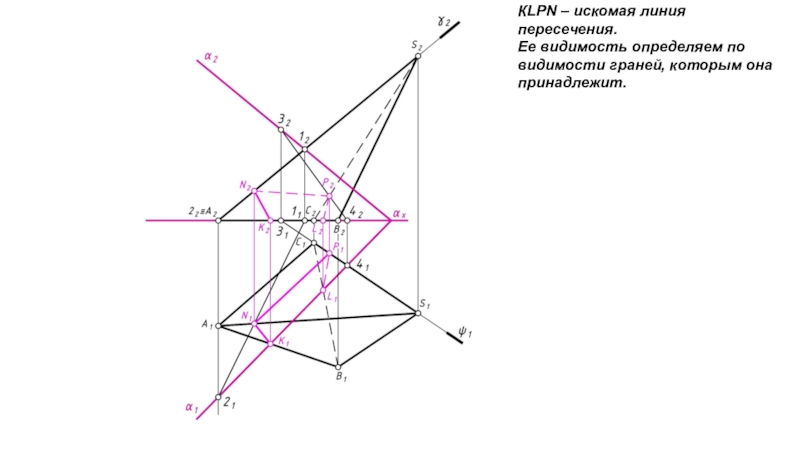
пересекает, т.к. она пересекает основание пирамиды.

Ребро SС пересекает плоскость α в точке Р:3242  S2С2 = Р2; Р1  S1С1 ;Ребро SB

Слайд 8КLPN – искомая линия пересечения.
Ее видимость определяем по видимости граней,

которым она принадлежит.

Слайд 9Определяем видимость поверхности и плоскости.

Слайд 103. Натуральную величину линии пересечения определяем способом вращения вокруг следа

плоскости (совмещения). Строим совмещенный след плоскости α.
Для этого нам нужно

иметь любую точку, принадлежащую следу α2 плоскости.
Чтобы избежать лишних построений, через точку Р проведем горизонталь h, принадлежащую α.
h2  α2 = 12, 11  ОХ. h1 // α1.

3. Натуральную величину линии пересечения определяем способом вращения вокруг следа плоскости (совмещения). Строим совмещенный след плоскости

Слайд 11Σ – плоскость вращения точки 1.
Σ1  α1.

Слайд 12Окр. (ц. т.αх, R= 12αх )  Σ1 = 10.

Слайд 13Через точки αх и 10 проводим совмещенный след плоскости α0.

Слайд 14Точки К и L принадлежат оси вращения, следовательно останутся неподвижными:
К1

 К0; L1  L0.

Слайд 15Строим совмещенную горизонталь h:
h0 проходит через точку 10 и параллельна

α1.
δ - Плоскость вращения точки Р.
h0  δ1 =

Р0.

Строим совмещенную горизонталь h:h0 проходит через точку 10 и параллельна α1. δ - Плоскость вращения точки Р.h0

Слайд 16Точку N0 строим аналогично.

Слайд 17Точку N0 строим аналогично.

Слайд 18К0L0P0N0 – н.в. KLPN.

Слайд 194. Для построения развертки пирамиды необходимо определить натуральные величины всех

ее ребер.
Основание АВС принадлежит П1, следовательно А1В1С1 – н.в.
Натуральные

величины ребер SA, SB, SC определяем вращением вокруг проецирующей оси i, проходящей через вершину пирамиды S (смотреть презентацию по вращению прямой вокруг проецирующей оси).

4. Для построения развертки пирамиды необходимо определить натуральные величины всех ее ребер.Основание АВС принадлежит П1, следовательно А1В1С1

Слайд 23Точки P и N можно также вращать вокруг оси i.

Однако, зная, что плоскости их вращения параллельны оси ОХ, и

исходя из свойства их принадлежности соответствующим ребрам пирамиды, можно упростить их нахождение.

Точки P и N можно также вращать вокруг оси i. Однако, зная, что плоскости их вращения параллельны

Разделы презентаций

Развертка усеченной поверхности

Содержание

Слайды и текст этой презентации

Слайд 1Развертка усеченной поверхности

Слайд 3Алгоритм решения:Основание пирамиды принадлежит плоскости проекций П1, горизонтальный след плоскости

α – α1 также принадлежит П1, следовательно: К1=А1В1  α1 ,

Слайд 42. Т.к. плоскость α занимает общее положение, то для нахождения

линии пересечения применим метод ребер. Последовательно заключим каждое из ребер

Слайд 5Ребро SА пересекает плоскость α в точке N:1121  S1А1

= N1; N2  S2А2;

Слайд 6Заключим ребро SC в горизонтально-проецирующую плоскость . Определяем линию пересечения 34

плоскости-посредника  с заданной плоскостью α: 1  ОХ = 31;

Слайд 7Ребро SС пересекает плоскость α в точке Р:3242  S2С2

= Р2; Р1  S1С1 ;Ребро SB плоскость α не

Слайд 8КLPN – искомая линия пересечения.Ее видимость определяем по видимости граней,

которым она принадлежит.

Слайд 9Определяем видимость поверхности и плоскости.

Слайд 103. Натуральную величину линии пересечения определяем способом вращения вокруг следа

плоскости (совмещения). Строим совмещенный след плоскости α.Для этого нам нужно

Слайд 11Σ – плоскость вращения точки 1. Σ1  α1.

Слайд 12Окр. (ц. т.αх, R= 12αх )  Σ1 = 10.

Слайд 13Через точки αх и 10 проводим совмещенный след плоскости α0.

Слайд 14Точки К и L принадлежат оси вращения, следовательно останутся неподвижными:К1

 К0; L1  L0.

Слайд 15Строим совмещенную горизонталь h:h0 проходит через точку 10 и параллельна

α1. δ - Плоскость вращения точки Р.h0  δ1 =